如何才能战胜市场？

1. 稳妥的思考框架。
   原则，方法论。
   
2. 情绪控制
   必须自己做到。压力应对。

面对未来的时机选择，风险管理。

巴菲特：价值投资，在别人恐惧时贪婪，在别人贪婪时恐惧。

降龙十八掌

投资需要平衡很多基本问题，面面俱到，又有机统一。

学习第二层次思维

• 环境的不可控+人心里的波动
• 第二层次思维
  在大众思维的基础上进行思考，反过来想。
  
  
• 第二层思维需要考虑的东西
  

几何学最早是丈量世界而诞生，从而抽象了现实的世界。
一个人想要谈论某个事物，前提是他必须弄清楚该事物的定义。定义和概念是很重要的，于数学及现实皆然。
学几何学的是其中的逻辑思想，特别是欧几里得几何的研究问题的方法。整个体系的建设，从几个不证自明的公理出发，通过推理、演绎，建立相关的定理、命题，搭建了整个壮丽的几何学大厦。基于不同的公理可以构建不同的几何体系，例如欧氏几何和非欧几何。
数学有很大一部分作用在于，厘清哪些事物是我们暂时或者永远都不用关心的，这种选择性注意是人类理性的基本组成部分。这其实也是抽象的过程，抽象就是省略细节，关注你研究重点的过程，例如算术关注的是数量，而事物的本身是什么并不重要；而拓扑学（庞加莱创立，研究洞的问题）关注的是形状，大小、距离反而不关心；而物理关心的是位置和速度；欧氏几何研究的是长度、面积等不变量。

给不同的事物赋予相同的名称

其实就是考虑研究的特征，把形同特征的事物归类为同一事物，也是一种抽象的过程。
庞加莱：数学是一门给不同事物赋予相同的名称的艺术。

很早就看完的一本书，吴军写的，放车上，一直没有做笔记，书套都找不到了 :），今天在咖啡厅就顺便做了，不过可能经济不景气的原因，咖啡厅的人倒是很少。
本书副标题“世界永远不缺聪明人”，一本心灵鸡汤汇编而成的书，有点像《论语》，主要是教做人的道理。想起赵普的半部论语治天下，这本书倒也可以放车上，偶尔看看。

看行业、看产业

例如现在的新能源？

一本比较别具一格的经济类的书，一共四本（佩服作者这么多口水），以案例为出发点，引出经济学的知识。很多观点还是别具一格，令人耳目一新，从常人想不到的角度提出一些新的、还挺有道理的观点。不过因为是以案例为主，整书知识显得有点凌乱，不够系统。
茶余饭后消遣看看可以，猎奇一下。想真正的系统的了解学习经济学就帮不上忙了。
道德代表了人类希望这个世界应该如何运转，而经济学则代表着其实际的运转方式。
经济学，从根本而言，是一门研究动机的学科：人如何得偿所愿或满足所需，尤其是其他人欲求相同的情况下。
人的动机分三大类:总体来说是利己、趋利避害。因为价值观不同，在面临三者的取舍时，不同人会做出不同的选择，例如海瑞会选择道德一样，所以说传统经济学中提出的经济人是理性的（经济动机），是不完全的。

• 经济动机
  
• 社会动机： 名声、从众心理、别人看法。
  
• 道德动机： 情绪价值、名声、负罪感等，自身的价值观。人心中的道德指南针，类似古话说的“心中的一杆秤”

利用信息差获利

信息就是权力、就是资源。互联网的作用本质上是消除了信息差。有句话说，领导的主要权力就是信息，领导往往比下面人的信息更多，更充分。
有时面对专家的咨询反而加剧了信息的不对称现象，因为专家会利用手中的信息资源优势来获取利益。或者利用信息差来制造恐惧心理，创造需求。
不说假话，但真话不说全，也是一种利用信息不对称获得优势地位的手段。

2022年9月份看的一本书，现在补上读书心得。
思考，个人如何面对经济危机？国家、企业呢？不同层级应该有不同的对策。

文章摘要

• 由于信贷同时创造了购买力和债务，因此增加信贷的好坏取决于能否把借款用于生产性目的，从而创造出足够多的收入来还本付息。
  PS：目前很多是借新债还旧债。
  
• 大量举债的风险主要是决策者能否有意愿和能力将坏账分摊到多年，取决于两个因素：
  短期债务长期化，让时间来解决问题的思想。
  1. 债务是否以决策者能够控制的货币计价；
     
  2. 决策者能否对债权人和债务人施加影响。
     
• 化繁就简地讲，你一旦借钱，就会创造出一个周期，买一件你目前买不起的东西，你的消费必然会超出你的收入，借款时，你不仅是向贷款人借钱，你实际上是向未来的自己借钱，在未来的某个时刻，你必须降低消费水平，以偿还债务。
  PS: 但借款用于生产就不一样。
  PS：所以借款必须考虑未来的收入预期。如果因为太乐观，导致未来某个时刻的收入不能覆盖相关债务，就发生经济危机。对一个国家、经济体和个人都一样。
  
• 决策者可以采取以下四种措施，以降低债务与收入之间的比率和偿债总额与用于偿债的现金流之间的比率。
  • 财政紧缩（即减少收入）
    
  • 债务违约/重组
    
  • 央行印钞，购买资产（或提供担保）
    
  • 将资金和信贷从充足的领域转向不足的领域。
• 和谐的去杠杆化
  降低债务和收入比率，同时保持适当的经济增长率和通胀率。
  但实际上很难，物极必反，往往都是快速下降的硬着陆方式（也就是说的自我强化），而不是缓缓下降的软着陆。就像地产。不过话说，挤掉泡沫，来一次置之死地而后生。
  例如房地产的三条红线，导致地产的偿债增加；同时由于地产房价的泡沫，导致需求减少，减低了收入，故出现地产的债务危机。
  
  阅读全文 »

一本关于统计学的普及类书籍，从宏观上介绍了统计学的主要概念和关键的原理。写得通俗易懂，作为一本入门的了解统计学的书籍来说还是不错的。
本书的主要目的是需要明白数学在生活中的意义，所以很多的例子是结合生活中的实际场景来展开的，使统计学的概念变得更加直观和便于理解。确实是，学习一门课程，考虑生活意义，从生活意义出发是让学生提高兴趣的最好的方法，避免一开始就进入枯燥的定理和公式，只会劝退大部分的学生。
统计学中重要的区分因果关系和相关性（具有统计学意义）。

统计学是大数据时代最炙手可热的学问

从抽样数据来解决大问题。统计学的一个核心功能就是使用手中已有的数据进行合理推测，以回答那些我们还未掌握所有信息的“大”问题。简而言之，我们能够使用“已知世界”的数据来对“未知世界”进行推断。

• 将一序列复杂数据浓缩成单一数字的应用。例如足球中会把一堆数据浓缩成一个单独的评分。
  
• 描述统计学存在的意义就是简化，因此不可避免的丢失一些内容和细节，方便对比和评价。（简化才能适应人的大脑，才容易传播，特别是面对公共领域的时候。），浓缩的技术、取舍权重不同导致不同的结果。人们喜欢看到简单的答案！
  
• 任何一个风险评估模型都必须以概率为基础。（概率的不确定性会导致黑天鹅事件的颠覆效应。）
  
• 统计学总是想告诉我们一些信息，但是面对这些信息，聪明而又诚实的人经常有不同的看法。

描述统计学

平均数、中位数、四分位数等。

• 25百分位和75百分位，通常作为中产阶级中的高收入和低收入人群。

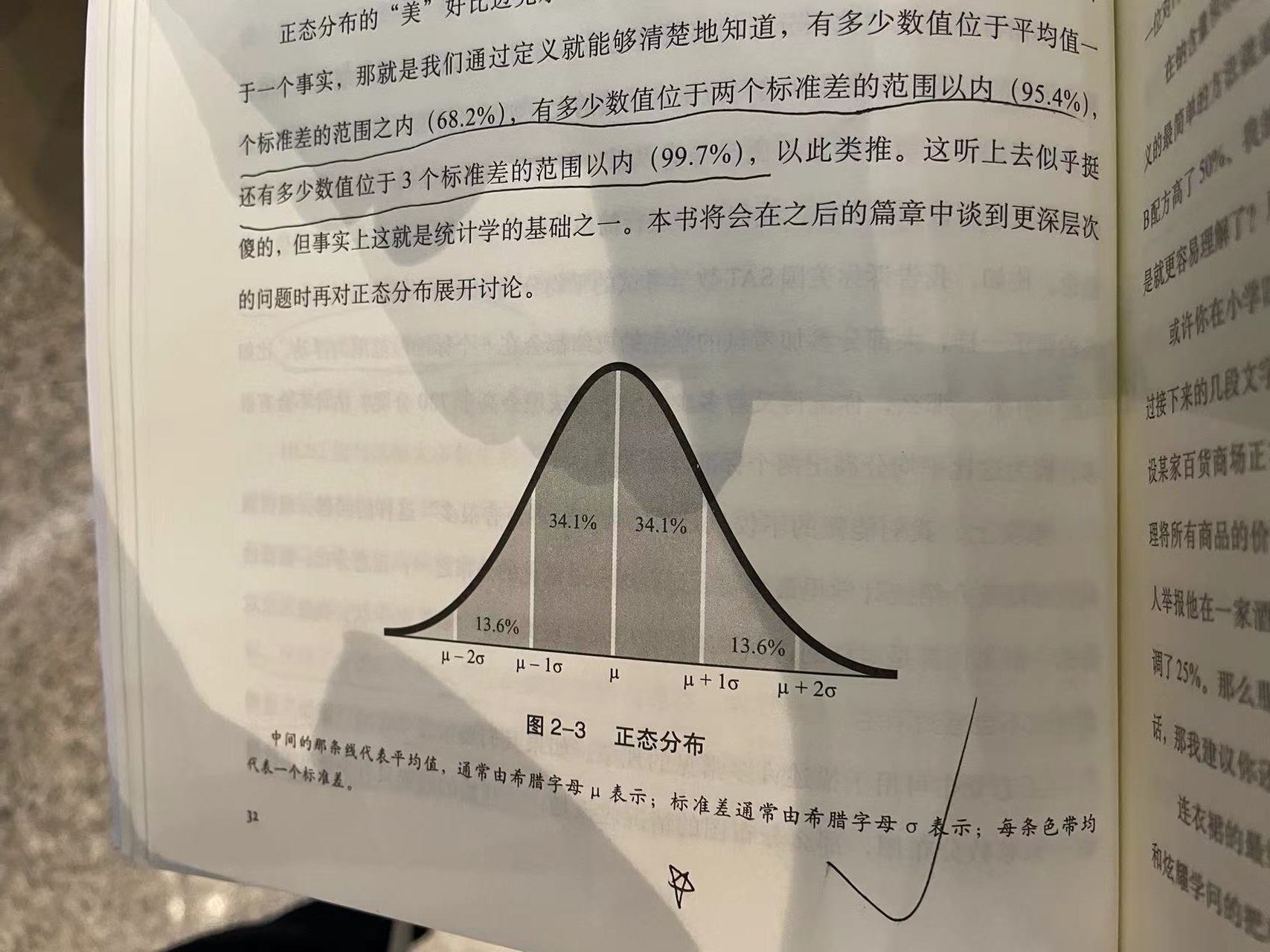
标准差也是一个能让我们在一堆杂乱无章的数字中发现真理的统计数值。我们用它来衡量数据相对于平均值的分散程度，根据标准差，我们可以知道所有观察数值的分散情况。
标准差和方差。

这几年的王阳明热，带来的结果就是市面上关于王阳明的书籍鱼目混珠。之前也看过一些这类型的书，看完后觉得写得最好的还是这一套书。
《王阳明大传》分上、中、下三卷，共三本。
此传记不同普通传记以故事驱动的做法，而是以王阳明思想的发展为主线，同步对比分析各种流派（儒、释、道）和人物（陆九渊、朱熹等）。是结合王阳明生涯及心学思想的一本宋明哲学史、思想史。
通过王阳明的诗词、文章、奏章，和亲朋好友的书信来往，以及门人关于王阳明的记录，分析了王阳明的人生轨迹及思想形成历程。本书更像一本严格考证的书，从中也可看出作者（日本人）严谨的治学态度。本书是从日语翻译过来的，译者的水平也很高，看起来就像一本中文大师级的水准，完全没有翻译的痕迹。

近年，王阳明的思想进入了主流的宣传，这也是政治的需要，王阳明的“致良知、知行合一”，确实是为官、为民的楷模。
不过哲学层面这些形而上的东西，有时候看起来特别绕，像是一种文字游戏。特别是在讲述朱熹的格物致知、知行二分和王阳明的知行合一的讨论，感觉怎么讲都对，就像一个硬币的两面，只是大家看待问题的角度不同罢了。

生平

王阳明，浙江余姚（属于绍兴）人，名守仁。他老爸王华，又称“龙山先生”，状元。
被贬贵州龙场（龙场悟道），在那里悟出了“心则理”的思想，并提出“知行合一”说。致良知是在晚年才提出，但致良知是阳明心学的根基。良知就是己所不欲，勿施于人。
王阳明是大圣人、大儒家、大豪杰，道德层面无出其右者，文学水平也高，同时，在军事层面也在文人中无可比拟。其三征的功绩在历史上都是赫赫之战功。
不过因奸臣诋毁，在政治上没有达到他对应的能力和功劳。

众所周知，王阳明因知行合一、致良知的思想而名闻天下。但就像一个人的成长一样，王阳明的思想也是在人生的不断磨砺中逐渐形成。
 
自古以来，江浙地区名人辈出，孕育出众多英雄豪杰、文人骚客。
王阳明，浙江余姚人（属绍兴），名守仁。他老爸王华，又称“龙山先生”，明朝成化十七年状元。
 
王阳明早年沉溺于道教、佛教，后期悟出了它们的不足，进而笃信儒学。
而导致王阳明思想发生巨大转变的核心也是关于对孝道的理解。所谓百善孝为先，这是儒学的根本，也是不同于道教、佛教的一种入世思想。俗话说：爹娘便是灵山佛，不敬爹娘敬甚人？
 
欲戴皇冠，必承其重。
从人物传记中收获的最大价值就是让自己明白，自身所谓的各种不如意，和那些名人经历的苦难相比，只能说是微不足道。
 
王阳明，被人们称作中国历史上两个半完人之一，一个是孔子，另一个就是王阳明，半个曾国藩。
 
王阳明是大圣人、大儒家、大豪杰。道德层面无出其右者，文学造诣也很高，在军事层面更是文人中的佼佼者，其军事的三征功绩在历史上都是赫赫之战功。
 
但即使是这么一位圣人，也因奸臣的诋毁，在政治上屡屡受到打压和迫害。
 
就像司马迁《报任少卿书》说的“盖西伯拘而演《周易》；仲尼厄而作《春秋》；屈原放逐，乃赋《离骚》”。
 
被贬到贵州龙场的王阳明，龙场悟道，在那里悟出了“心则理”的思想和“知行合一”的学说，并在晚年提出了“致良知”。形成了“知行合一、致良知”的思想体系。
 
“致良知”是阳明心学的根基，良知就是己所不欲，勿施于人。而“知行合一”就必须要在事上磨炼。读万卷书不如行万里路，知行合一讲究的是实践。  

本书的例子，很适合做统计分析论文的参考。其分析的方法和思想很规范。

M0，M1，M2

各国央行都以流动性为依据对货币进行层次划分。

M1 流动性，目的是交易
M2 M1+储蓄 （现在主要是看M2的情况。）

本书的写作目的之一是在于构建一个过去思维（也就是‘历史’）与未来思维的连接案例，这样我们就能更好的用过去取照亮可能的未来。
作者通过人类对时间的理解，讲述了A、B两种时间序列的理解。然后分析生物通过神经系统的机制，如何应对未来进行说明。特别是人类有意识管理未来的方面，作者也做了分析和预测。总体来说是一个关于未来不错的一本书，也类似于人工智能的剖析，把动植物、人类的对未来的处理机制进行了较好的阐述。