《机器学习的数学基础》(2/7)
读书笔记之二:线性代数
2、线性代数
Linear Algebra
在形式化一些直观概念时,常见的方法是构造一组对象(符号)和一些操作这些对象的规则。 这就是所谓的代数(algebra)。线性代数是研究向量以及使用某些确定的规则来操作向量的 一门学科。 我们许多人从学校里知道的向量被称为“几何向量”,通常用上方带一个小箭头的字母表示。
向量是特殊的对象,将它们相加并乘以标量产生的是另一个相同类型的对象。从抽象的数学来看,任何满足这两个性质的物体都可以被认为是向量。
2.1 线性方程求解
出于数值精度的原因,通常不建议计算逆或伪逆。因此,在下文中,我们将简要讨论求解线性方程组的其他方法。
高斯消元法在计算行列式、检查向量集是否线性独立、计算矩阵的逆,计算矩阵的秩,和确定向量空间的基时起着重要作用。高斯消元法是一种直观而有建设性的方法来解决一个含成千上万变量的线性方程组。然而,对于具有数百万个变量的方程组,这是不切实际的,因为所需的运算量是按联立方程组的数量的立方增长的。
在实践中,许多线性方程组都是通过定常迭代方法(stationary iterative methods)间接求解的,如Richardson方法、Jacobi方法、Gauß-Seidel方法和逐次超松弛方法,或Krylov子空间方法,如共轭梯度、广义最小残差或双共轭梯度。
2.2 群
群的概念,它包含一组元素和一个定义在这些元素上的操作,该操作可以保持集合的某些结构完整。
- 封闭性(Closure)
- 结合律(Associativity)
- 单位元(Neutral elemen)
- 逆元(Inverse element)
群在计算机科学中扮演着重要的角色。除了为集合上的运算提供一个基本框架外,它们还被大量应用于密码学、编码理论和图形学。
如果可交换运算顺序,是阿贝尔群( Abelian group)(个人注:很多时候交换律都不是必须的。)
向量空间的定义太赞了,通过群的定义引出!
2.3 线性变换的定义
保持向量空间结构不变需满足:
\[ \forall x, y \in V\ \forall \lambda, \psi \in \mathbb{R} : \Phi(\lambda \mathbf{x} + \psi \mathbf{y}) = \lambda \Phi(\mathbf{x}) + \psi \Phi(\mathbf{y}). \]
我们可以把线性映射用矩阵(2.7.1节)表示。回想一下前面的内容:我们将向量集合用矩阵的列表示。在处理矩阵时,我们必须判断矩阵所表示的内容:是线性映射还是向量集合。
空间结构不变的定义:
从几何角度理解线性变换保持空间结构不变,可以帮助直观掌握线性变换的本质。
1、线性变换几何视角的理解
线性变换 \(\Phi: V \to W\) 是一种映射,满足:
- 加法保持:\(\Phi(\mathbf{x} + \mathbf{y}) = \Phi(\mathbf{x}) + \Phi(\mathbf{y})\)
- 数乘保持:\(\Phi(\lambda \mathbf{x}) = \lambda \Phi(\mathbf{x})\)
这意味着:
1)直线映射为直线 任何向量空间中的直线(即所有形如 \(\mathbf{v}_0 + t\mathbf{v}\) 的点集,其中 \(t \in \mathbb{R}\))经过线性变换后,仍然是直线(或退化成一点)。换句话说,线性变换不会把直线扭曲成曲线。(详见”向量空间中直线的定义.md“)
2)原点保持不变 由于 \(\Phi(\mathbf{0}) = \mathbf{0}\),线性变换一定把原点映射为原点。这保持了空间的“参考点”。
3)比例保持 对于任意标量 \(\lambda\),线性变换保证拉伸或压缩比例保持。例如,\(\mathbf{x}\) 拉伸两倍后变为 \(2\mathbf{x}\),变换后也是变换 \(\Phi(\mathbf{x})\) 的两倍:\(\Phi(2\mathbf{x}) = 2\Phi(\mathbf{x})\)。
4)平行保持 如果两条线在原空间平行,那么它们的像也平行(或者重合)。这是因为线性变换保持向量加法关系。
5)向量加法的几何含义保持 变换前后,向量的组合关系(比如三角形的顶点、平行四边形的形状)在变换后的空间里依然成立(尽管大小和方向可能改变)。
2、换句话说
线性变换是“刚性”变换的一个推广,它可以拉伸、压缩、旋转、反射空间,但不会产生弯曲或折叠,也不会“撕裂”空间结构。它保持了“直线”、“比例”、“原点”这些最基础的几何性质。
3、举个例子
- 旋转 是线性变换,保持长度和角度(保持空间结构不变的同时还保持距离)。
- 缩放(拉伸/压缩)也是线性变换,改变大小但不改变“直线性”和“比例”。
- 投影 是线性变换,把三维空间映射到二维平面,保持直线的映射,但改变维度和形状。
2.4 变换矩阵
注意变换矩阵(transformation matrix)的定义。使用变换矩阵将相对于\(V\)的有序基的坐标映射到相对于\(W\)中有序基的坐标。
后文提到,为了简化变换矩阵,通过基变换处理。
在矩阵和有限维向量空间之间的线性映射之间建立一个显式联系(重点是理解线性变换和矩阵之间的本质联系!)。
2.5 相似矩阵
如果存在可逆矩阵 \(\boldsymbol{P}\),使得 \[ \boldsymbol{D} = \boldsymbol{P}^{-1} \boldsymbol{A} \boldsymbol{P} \] 则称矩阵 \(\boldsymbol{A}\) 与 \(\boldsymbol{D}\) 是相似(Similarity)的(定义 2.22)。
2.6 恒等映射
\(\mathrm{id}_V : V \to V,\ x \mapsto x\) 为 \(V\) 中的恒等映射或单位自同构(详见文件:‘恒等映射的存在意义.md“)。
2.7 基变换
重要的作用:同一个点,在不同的基的不同坐标表示!变换矩阵相当于坐标的映射(不同基)。
在第四章中,我们将利用基变换的概念来寻找一个基,使得自同态的变换矩阵有一个特别简单的(对角)形式。在第十章降维中,我们将利用基变换研究一个数据压缩问题,即找到一个基并在这个基上投影数据从而压缩数据,同时最小化压缩损失。
2.8 变量变换和基变换区别
要分清楚基变换和变量变换的区别!不要混淆;两者得出的变换矩阵是不同的。
1、变量变换
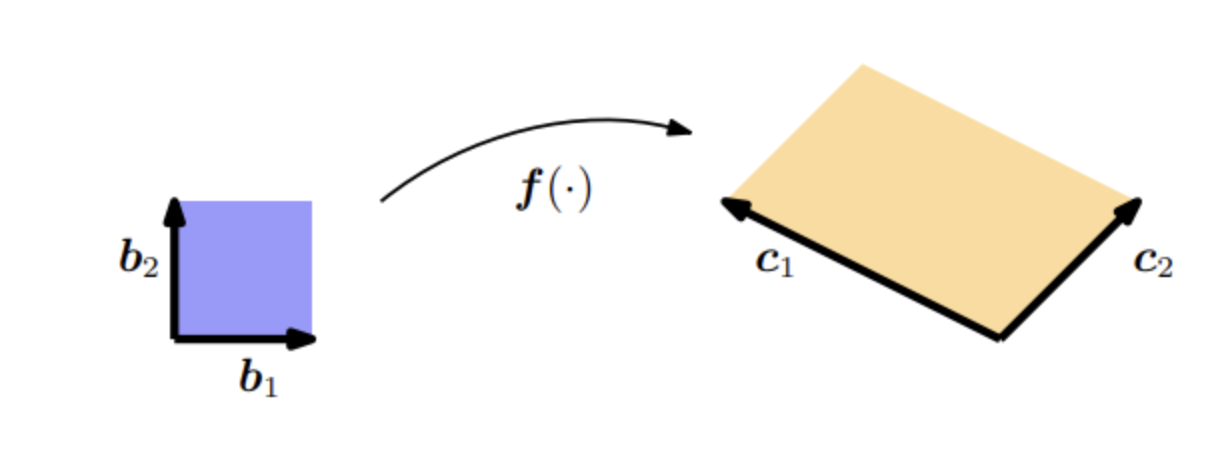
如果给定两个向量 \(\boldsymbol{b}_{1} = [1,0]^{\top}, \ \boldsymbol{b}_{2} = [0,1]^{\top}\) 作为单位正方形(图5.5中的蓝色区域)的边,则该正方形的面积为: \[ \left|\det\!\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\right| = 1 \]
如果我们取一个平行四边形(图5.5中的橙色区域),它的边为 \(\boldsymbol{c}_{1} = [-2,1]^{\top}, \ \boldsymbol{c}_{2} = [1,1]^{\top}\), 则它的面积是行列式(见第4.1节)的绝对值: \[ \left|\det\!\begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix}\right| = |-3| = 3 \]
即它的面积正好是单位方形的三倍。我们可以通过一个将单位方形转换成另一个方形的映射来找到这个缩放因子。用线性代数的术语说,就是有效地执行从 \((\boldsymbol{b}_{1}, \boldsymbol{b}_{2})\) 到 \((\boldsymbol{c}_{1}, \boldsymbol{c}_{2})\) 的变量变换。在我们的例子中,这个映射是线性的,且它的行列式的绝对值正好给出了我们要寻找的缩放因子。
因为\(\boldsymbol{b}_{1},\boldsymbol{b}_{2}\)是基,根据变换矩阵的定义,故变换矩阵是: \[ A = \begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix} \]
2、基变换
为了开始使用线性代数的方法,我们首先确定 \(\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}\) 和 \(\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}\) 都是 \(\mathbb{R}^2\) 的基。我们要有效地执行的是从 \(\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}\) 到 \(\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}\) 的基变换,就得寻找实现基变换的变换矩阵。 利用第2.7.2节的结果,我们确定了所需的基变换矩阵为: \[ \boldsymbol{J} = \begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix} \tag{5.62} \]
它使得 \(\boldsymbol{J}\boldsymbol{b}_{1} = \boldsymbol{c}_{1}, \quad \boldsymbol{J}\boldsymbol{b}_{2} = \boldsymbol{c}_{2}\)。 矩阵 \(\boldsymbol{J}\) 的行列式的绝对值为: \[ \left|\det(\boldsymbol{J})\right| = 3, \] 这正是我们在寻找的缩放因子。也就是说, \((\boldsymbol{c}_{1}, \boldsymbol{c}_{2})\) 所张成的平行四边形的面积是 \((\boldsymbol{b}_{1}, \boldsymbol{b}_{2})\) 所张成面积的三倍。
把 \(\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}\) 坐标变换成 \(\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}\) 的坐标,是左乘\(\boldsymbol{J}^{-1}\);反向是左乘\(\boldsymbol{J}\)。
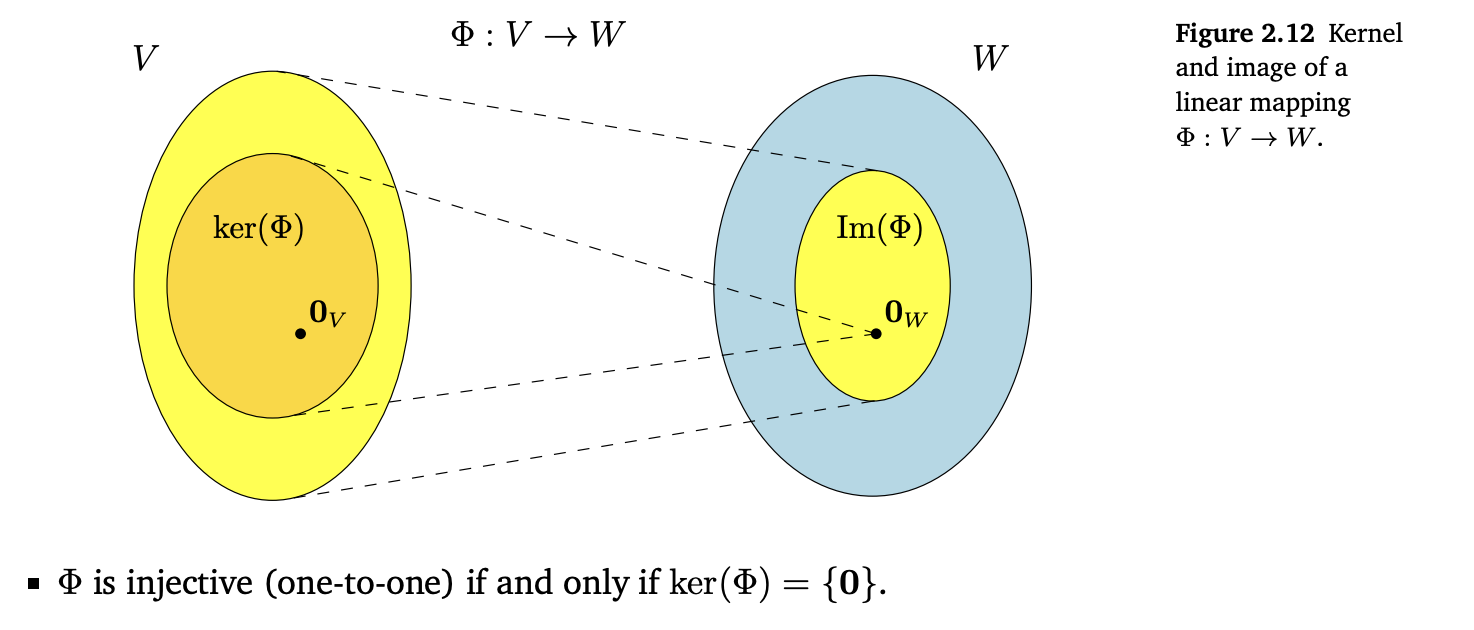
2.8 像与核
“直观地说,核是被 \(\Phi\) 映射到单位元 \(\mathbf{0}_W \in W\) 上的一组向量 \(\mathbf{v} \in V\)。”
具体见原书图2.12
2.9 仿射空间
在下面,我们将研究从原点偏移的空间,即不再是向量子空间的空间。此外,我们将简要讨论这些仿射空间之间类似线性映射的一些性质。
备注: 在机器学习领域的文献中,线性和仿射之间的区别有时是不明确的,因此我们可以将线性空间/映射作为仿射空间/映射的参考。
2.10 仿射映射
仿射映射保持几何结构不变。它们还保留了尺寸比例和平行度。
全书的读书笔记(共7篇)如下:
《机器学习的数学基础》读书笔记之一 :导言
《机器学习的数学基础》读书笔记之二 :线性代数
《机器学习的数学基础》读书笔记之三 :解析几何
《机器学习的数学基础》读书笔记之四 :矩阵分解
《机器学习的数学基础》读书笔记之五 :向量微积分
《机器学习的数学基础》读书笔记之六 :概率与分布
《机器学习的数学基础》读书笔记之七 :连续优化