《机器学习的数学基础》（4/7）

4、矩阵分解

Matrix Decomposition

在本章中，我们将介绍矩阵的三个方面：如何概括矩阵，如何分解矩阵，以及如何利用矩阵分解进行矩阵近似，矩阵分解的一个类比是因数分解(factoring of numbers)。

4.1 行列式与迹

• 行列式只适用于方阵。

• 可以看作是将矩阵映射到一个实数的函数。

• 当且仅当行列式不等于0时，矩阵可逆。

• 上三角（下三角）矩阵的行列式是其对角元素的积。

• 行列式度量体积；列向量代表各条边。

• 一个方阵 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\) 的行列式 \(\operatorname{det}(\boldsymbol{A}) \neq 0\)，当且仅当 \(\operatorname{rk}(\boldsymbol{A}) = n.\)换句话说，\(\boldsymbol{A}\) 可逆当且仅当它是满秩的

为什么：行列式只适用于方阵。
行列式衡量方阵线性变换的体积(面积、体积、n维体积)对应的变化，而非方阵既不构成同维线性变换，也不满足代数定义，并且可逆只针对方阵有意义。

对于 \(n \times n\) 矩阵的行列式，需要一个通用的算法来解决 \(n > 3\) 的情况，我们将在下面探讨这个问题。定理 4.2 将计算 \(n \times n\) 矩阵的行列式的问题简化为计算 \((n - 1) \times (n - 1)\) 矩阵的行列式。通过递归地应用拉普拉斯展开（Laplace Expansion），我们最终可以通过计算 \(2 \times 2\) 矩阵的行列式来计算 \(n \times n\) 矩阵的行列式。

行列式具有以下特性：

• 矩阵相乘的行列式是相应行列式的乘积，即

\[ \operatorname{det}(\boldsymbol{AB}) = \operatorname{det}(\boldsymbol{A}) \operatorname{det}(\boldsymbol{B}) \]

• 矩阵转置不改变行列式的值，即

\[ \operatorname{det}(\boldsymbol{A}) = \operatorname{det}(\boldsymbol{A}^{\top}) \]

• 如果 \(\boldsymbol{A}\) 是正则的（可逆的），

\[ \operatorname{det}(\boldsymbol{A}^{-1}) = \frac{1}{\operatorname{det}(\boldsymbol{A})} \]

• 相似矩阵（定义 2.22）具有相同的行列式。因此，对于线性映射 \(\Phi: V \rightarrow V\)，\(\Phi\) 的所有变换矩阵 \(\boldsymbol{A}_\Phi\) 都具有相同的行列式。因此，线性映射基的选择不影响行列式的值。（注意前提是\(V \rightarrow V\)）

• 将一列/行的倍数加到另一列/行不会更改 \(\operatorname{det}(\boldsymbol{A})\)。

• 用标量 \(\lambda \in \mathbb{R}\) 乘矩阵 \(\boldsymbol{A}\) 的行/列，将 \(\lambda\) 倍缩放 \(\operatorname{det}(\boldsymbol{A})\)。特别地，

\[ \operatorname{det}(\lambda \boldsymbol{A}) = \lambda^n \operatorname{det}(\boldsymbol{A}) \]

• 交换两行/列将更改 \(\operatorname{det}(\boldsymbol{A})\) 的符号。

迹

方阵 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\) 的迹（trace）定义为：

\[ \operatorname{tr}(\boldsymbol{A}) := \sum_{i=1}^{n} a_{ii} \]

即，迹是 \(\boldsymbol{A}\) 的对角元素之和。

迹满足以下属性：

1. 对于 \(\boldsymbol{A}, \boldsymbol{B} \in \mathbb{R}^{n \times n}\)，有：

\[ tr⁡(A+B)== \operatorname{tr}(\boldsymbol{A}) + \operatorname{tr}(\boldsymbol{B}) \]

2. 对于 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\)，\(\alpha \in \mathbb{R}\)，有：

\[ tr⁡(αA) = \alpha \operatorname{tr}({A}) \]

3. 单位矩阵的迹为：

\[ tr⁡(In) = n \]

4. 对于 \(\boldsymbol{A} \in \mathbb{R}^{n \times k}\)，\(\boldsymbol{B} \in \mathbb{R}^{k \times n}\)，有：

\[ tr⁡(AB)= \operatorname{tr}({B}{A}) \]

可以证明，只有一个函数同时满足这四个性质——即迹（Gohberg et al., 2012）。

线性映射的矩阵表示依赖于基，而线性映射\(\phi\)的迹独立于基。 具体原理见资料《迹的相似不变性.md》

特征多项式:

将行列式和迹作为描述方阵的函数来讨论。

对于 \(\lambda \in \mathbb{R}\) 和一个方阵 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\)，其特征多项式（Characteristic Polynomial）定义为：

\[ p_A(\lambda) := \det(\boldsymbol{A} - \lambda \boldsymbol{I}) = c_0 + c_1 \lambda + c_2 \lambda^2 + \cdots + c_{n-1} \lambda^{n-1} + (-1)^n \lambda^n \]

其中 \(c_0, \ldots, c_{n-1} \in \mathbb{R}\)。特别地，

\[ c_0 = \det(\boldsymbol{A}), \quad c_{n-1} = (-1)^{n-1} \operatorname{tr}(\boldsymbol{A}) \]

特征多项式将允许我们计算特征值和特征向量。

4.2 特征值和特征向量

指向同一方向的两个向量称为共向的(codirected)。如果两个向量指向相同或相反的方向，则它们是共线的（collinear）。

令 \(A \in \mathbb{R}^{n \times n}\) 为一个方阵。

\[ \boldsymbol{A}\boldsymbol{x} = \lambda \boldsymbol{x} \]

我们称这个方程为特征方程（eigenvalue equation）。其中 \(\lambda \in \mathbb{R}\) 为 \(\boldsymbol{A}\) 的特征值（eigenvalue），\(\boldsymbol{x} \in \mathbb{R}^{n} \setminus \{\boldsymbol{0}\}\) 为相应的特征向量（eigenvector）。

以下说法是等效的（个人注：详见《特征值和齐次方程解的关系.md》）：

1. \(\lambda\) 是 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\) 的特征值。
   
2. 存在 \(\boldsymbol{x} \in \mathbb{R}^{n} \backslash \{\mathbf{0}\}\)，使得 \(\boldsymbol{A}\boldsymbol{x} = \lambda \boldsymbol{x},\) 或等价地 \((\boldsymbol{A} - \lambda \boldsymbol{I}_{n}) \boldsymbol{x} = \mathbf{0}\) 有非平凡解，即 \(\boldsymbol{x} \neq \mathbf{0}\)。
   
3. \(\operatorname{rk}\!\left(\boldsymbol{A} - \lambda \boldsymbol{I}_{n}\right) < n\)
   
4. \(\det\!\left(\boldsymbol{A} - \lambda \boldsymbol{I}_{n}\right) = 0\)

特征空间和特征谱:

对于 \(A \in \mathbb{R}^{n \times n}\)，\(\boldsymbol{A}\) 对应于特征值 \(\lambda\) 的特征向量集合张成 \(\mathbb{R}^{n}\) 的子空间，这个子空间称为 \(\boldsymbol{A}\) 关于 \(\lambda\) 的特征空间（eigenspace），记为：\(E_{\lambda}\) ; \(\boldsymbol{A}\) 的特征值构成的集合称为特征谱（eigenspectrum），或 \(\boldsymbol{A}\) 的谱。

特征值为 0 的特征向量是矩阵零空间中的非零向量；它揭示了矩阵在某些方向上把向量“压扁”为零；

单位矩阵 \(\boldsymbol{I} \in \mathbb{R}^{n \times n}\) 的特征方程为：

\[ P_{I}(\lambda) = \operatorname{det}(\boldsymbol{I} - \lambda \boldsymbol{I}) = (1 - \lambda)^n = 0 \]

它只拥有 \(\lambda = 1\) 这个特征值，并出现 $ n $ 次。而且，对于任意 \(\boldsymbol{x} \in \mathbb{R}^{n} \setminus \{\boldsymbol{0}\}\)，有：

\[ \boldsymbol{I} \boldsymbol{x} = \lambda \boldsymbol{x} = 1 \cdot \boldsymbol{x} \]

因此，单位矩阵的唯一特征空间 \(E_1\) 张成 \(n\) 维，\(\mathbb{R}^{n}\) 的 \(n\) 个标准基向量都是 \(\boldsymbol{I}\) 的特征向量。(另外：单位矩阵保持所有方向不变，因此所有方向都是特征向量)。

关于特征值和特征向量的常用特性包括：

• 矩阵 \(\boldsymbol{A}\) 及其转置 \(\boldsymbol{A}^{\top}\) 具有相同的特征值，但不一定具有相同的特征向量。

• 特征空间 \(E_{\lambda}\) 是 \(\boldsymbol{A} - \lambda \boldsymbol{I}\) 的零空间，因为：

\[ \boldsymbol{A} \boldsymbol{x} = \lambda \boldsymbol{x} \Longleftrightarrow \boldsymbol{A} \boldsymbol{x} - \lambda \boldsymbol{x} = \boldsymbol{0} \Longleftrightarrow (\boldsymbol{A} - \lambda \boldsymbol{I}) \boldsymbol{x} = \boldsymbol{0} \Longleftrightarrow \boldsymbol{x} \in \ker(\boldsymbol{A} - \lambda \boldsymbol{I}) \]

• 相似矩阵（定义 2.22）具有相同的特征值。基变换得到的是相似矩阵。因此，线性映射 \(\Phi\) 的特征值与它的变换矩阵的基的选择无关。这使得特征值、行列式和迹成为线性映射的重要不变量。

• 对称正定矩阵总是有正的实特征值。

假设：

• \(A\) 是一个线性变换在基底\(\mathcal{B}\) 下的矩阵
  
• 换到另一个基底\(\mathcal{C}\) ，基变换矩阵为 \(P\)

那么在新基底下的矩阵是：
\[ A' = P^{-1} A P \]

这就叫 相似矩阵（similar matrix）。
上式右边过程：P作用在新基上坐标转换成旧基坐标，用A做变换，然后转换成新基坐标。详见“线性代数“的“2.8 变量变换和基变换区别“。

剪切映射：

剪切映射（Shearing Mapping） 是一种保持某些几何特征（如面积、体积）不变，但改变形状的线性变换。在二维或三维欧几里得空间中，它通过“滑动”坐标轴方向的某些分量，使图形在不旋转也不缩放的前提下发生倾斜变形。
几何直观：

• 剪切会把一个矩形变成平行四边形。
  
• 面积保持不变。
  
• 角度和形状会改变，但线之间的平行关系保持。
  
• 单位正方形在剪切后变成平行四边形，但底边长度不变。

详见《剪切映射的变换矩阵.md》

一个矩阵 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\) 的 \(n\) 个特征向量 \(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{n}\) 对应 \(n\) 个不同的特征值 \(\lambda_{1}, \ldots, \lambda_{n}\)，则它们是线性独立的。这个定理指出，具有 \(n\) 个不同特征值的矩阵的特征向量构成 \(\mathbb{R}^{n}\) 的一组基。
给定一个矩阵 \(\boldsymbol{A} \in \mathbb{R}^{m \times n}\)，我们总能通过\(\boldsymbol{S} := \boldsymbol{A}^{\top} \boldsymbol{A}\) 得到一个对称的半正定矩阵\(\boldsymbol{S} \in \mathbb{R}^{n \times n}\)。
注：很多地方只需要半正定矩阵即可。

4.3 谱定理

Spectral Theorem

如果 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\) 是对称的，则存在 \(\boldsymbol{A}\) 的特征向量组成向量空间 \(V\) 的一个正交基，且每个特征值都是实数。

谱定理的直接含义是：对称矩阵 \(\boldsymbol{A}\) 存在特征值分解（具有实特征值），并且我们可以由特征向量构造一个标准正交基，使得 \[ \boldsymbol{A} = \boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{\top}, \] 其中 \(\boldsymbol{D}\) 是对角矩阵，\(\boldsymbol{P}\) 的列是 \(\boldsymbol{A}\) 的单位特征向量，满足 \(\boldsymbol{P}^{\top} \boldsymbol{P} = \boldsymbol{I}\)。

4.4 特征值、特征向量、行列式、迹的联系

定理 4.16：

设矩阵 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\)，则其行列式等于其所有特征值的乘积，即 \[ \det(\boldsymbol{A}) = \prod_{i=1}^{n} \lambda_i \] 其中 \(\lambda_i \in \mathbb{C}\)（可重复）为矩阵 \(\boldsymbol{A}\) 的特征值。

定理 4.17：

设矩阵 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\)，则其迹等于其所有特征值的和，即 \[ \operatorname{tr}(\boldsymbol{A}) = \sum_{i=1}^{n} \lambda_i \] 其中 \(\lambda_i \in \mathbb{C}\)（可重复）为矩阵 \(\boldsymbol{A}\) 的特征值。

4.5 矩阵分解

Matrix Decomposition

4.5.1 Cholesky分解

对称正定矩阵 \(\boldsymbol{A}\) 可以分解为： \[ \boldsymbol{A} = \boldsymbol{L} \boldsymbol{L}^{\top}, \] 其中 \(\boldsymbol{L}\) 是具有正对角元素的下三角矩阵。 \(\boldsymbol{L}\) 被称为 \(\boldsymbol{A}\) 的Cholesky 因子（Cholesky factor），且是唯一的。对称正定矩阵的类平方根运算，即Cholesky分解。

4.5.2 特征值分解与对角化

矩阵 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\) 的对角化，实际是在另一个基中表示相同线性映射的一种方法，这个基由 \(\boldsymbol{A}\) 的特征向量组成。

定理 4.20特征值分解，Eigendecomposition

设 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\)，则当且仅当 \(\boldsymbol{A}\) 有 \(n\) 个线性无关的特征向量时，\(\boldsymbol{A}\) 可以被对角化，即存在可逆矩阵 \(\boldsymbol{P}\) 和对角矩阵 \(\boldsymbol{D}\)，使得： \[ \boldsymbol{A} = \boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{-1} \]

其中：\(\boldsymbol{P} \in \mathbb{R}^{n \times n}\) 的列是 \(\boldsymbol{A}\) 的 \(n\) 个线性无关的特征向量；\(\boldsymbol{D}\) 是对角矩阵，其对角元素为 \(\boldsymbol{A}\) 的特征值（可重复）；因此，只有当 \(\boldsymbol{A}\) 的特征向量张成 \(\mathbb{R}^n\)，即 \(\boldsymbol{A}\) 是非亏损的，\(\boldsymbol{A}\) 才可以对角化。

定理 4.21对称矩阵的特征值分解

设 \(\boldsymbol{S} \in \mathbb{R}^{n \times n}\) 是对称矩阵（即 \(\boldsymbol{S}^{\top} = \boldsymbol{S}\)），则 \(\boldsymbol{S}\) 一定可以被对角化。

根据谱定理，对于任意对称矩阵 \(\boldsymbol{S}\)，存在一个标准正交基，由 \(\boldsymbol{S}\) 的特征向量构成。即存在正交矩阵 \(\boldsymbol{P}\)，使得：

\[ \boldsymbol{S} = \boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^\top \]

其中：

• \(\boldsymbol{P} \in \mathbb{R}^{n \times n}\) 是正交矩阵，列向量为单位正交的特征向量；
• \(\boldsymbol{D}\) 是对角矩阵，对角元素为 \(\boldsymbol{S}\) 的特征值；
• 此分解方式也可表示为 \(\boldsymbol{D} = \boldsymbol{P}^\top \boldsymbol{S} \boldsymbol{P}\)。

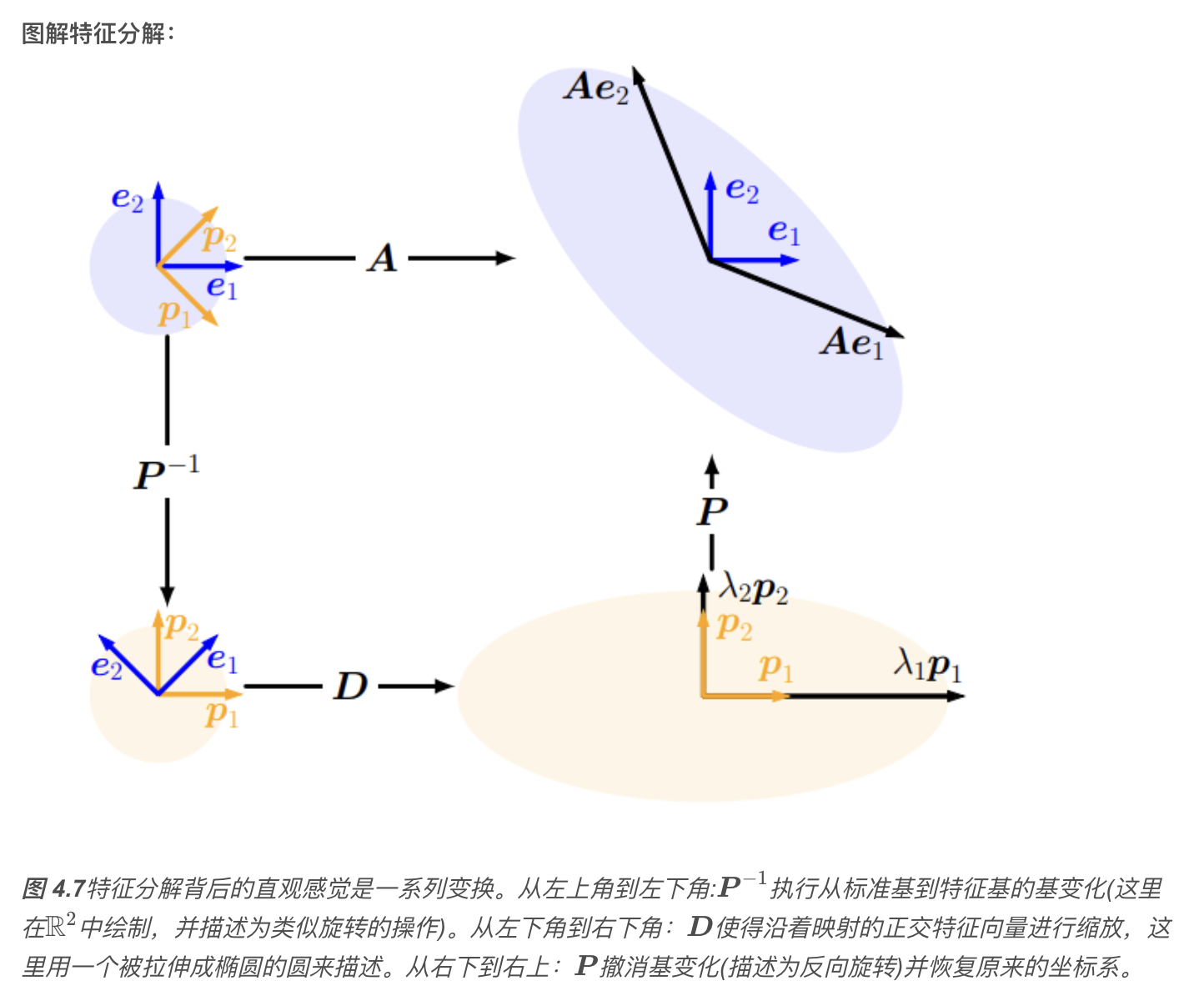
在相同的向量空间中应用相同的基变化，然后撤消。

4.5.3 奇异值分解

singular value decomposition, SVD

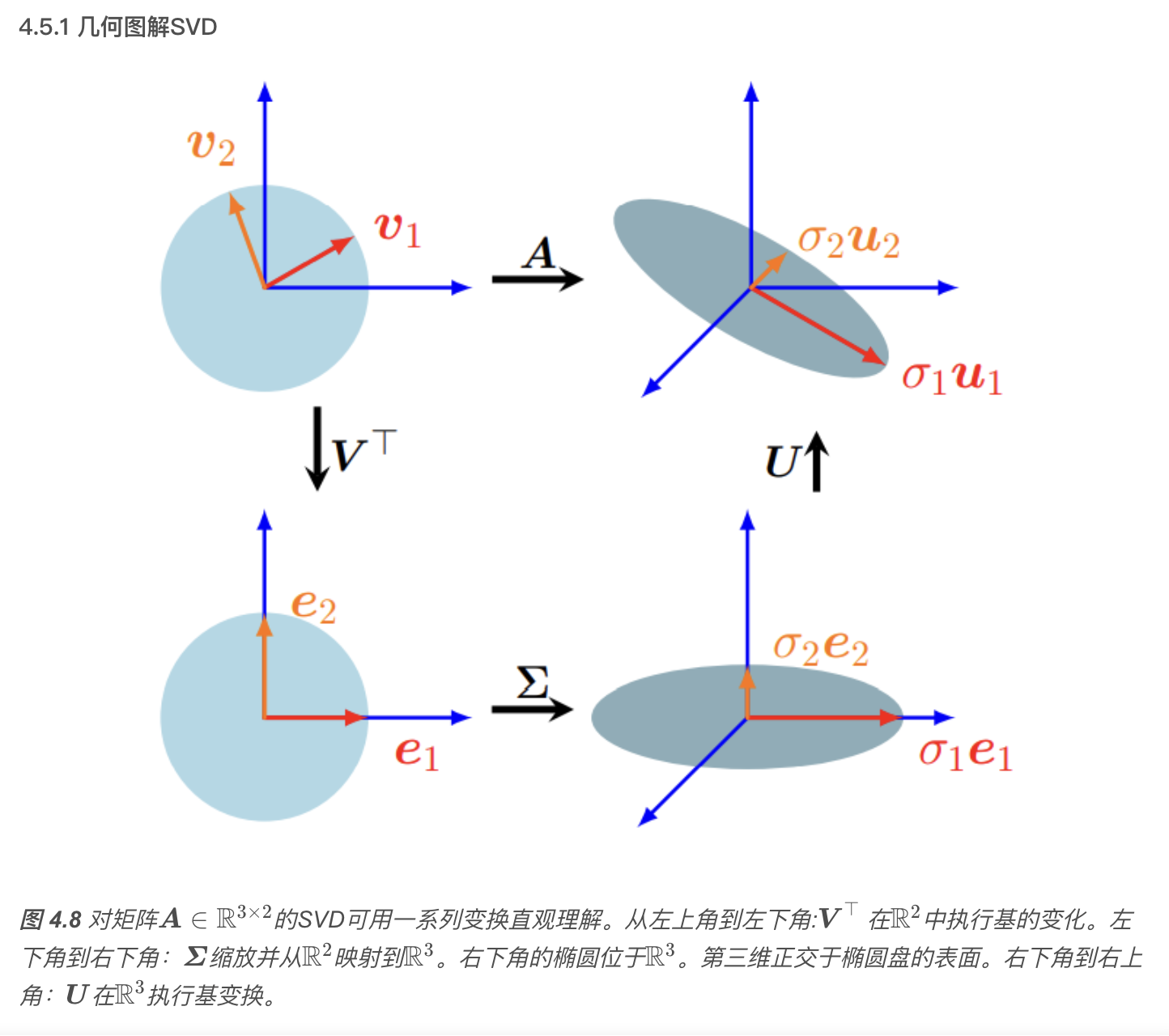
表示线性映射 \(\Phi: V \rightarrow W\) 的矩阵 \(\boldsymbol{A}\) 的奇异值分解量化了这两个向量空间的潜在几何变化。

奇异值分解（SVD）公式

\[ \boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^\top \]

以及它在几何上的意义（旋转+缩放+旋转）.

其中 \(\boldsymbol{U} \in \mathbb{R}^{m \times m}\) 为正交矩阵，其列向量为 \(\boldsymbol{u}_i, \ i=1, \ldots, m\)；\(\boldsymbol{V} \in \mathbb{R}^{n \times n}\) 也为正交矩阵，其列向量为\(\boldsymbol{v}_i, \ i=1, \ldots, n\)。另外，\(\boldsymbol{\Sigma}\) 为 \(m \times n\) 矩阵，且\(\Sigma_{ii} = \sigma_i \geqslant 0, \quad \Sigma_{ij} = 0, \ i \neq j .\) \(\boldsymbol{\Sigma}\) 的对角元素\(\sigma_i, \quad i = 1, \ldots, r\)称为奇异值（singular values），\(\boldsymbol{u}_i\) 称为左奇异向量（left-singular vectors），\(\boldsymbol{v}_i\) 称为右奇异向量（right-singular vectors）。按照惯例，奇异值是有序的：\(\sigma_1 \geqslant \sigma_2 \geqslant \cdots \geqslant \sigma_r \geqslant 0 .\)

奇异值矩阵 \(\boldsymbol{\Sigma}\) 是唯一的。需要注意 \(\boldsymbol{\Sigma} \in \mathbb{R}^{m \times n}\) 是矩形的，且与 \(\boldsymbol{A}\) 尺寸相同。这意味着 \(\boldsymbol{\Sigma}\) 有一个包含奇异值的对角子矩阵，其他元素为零。

注1：SVD 对任意 \(\boldsymbol{A} \in \mathbb{R}^{m \times n}\) 都成立。
注2：旋转矩阵就是一个行列式为 \(+1\) 的正交矩阵，也就是： \(R^\top R = I, \quad \det(R) = 1\)
注3：标准正交基(ONB)
注4：左奇异向量和右奇异向量的直观理解，详见《SVD 中的左奇异向量和右奇异向量.md》

4.5.4 特征值分解 vs. 奇异值分解

考虑特征值分解 \[ \boldsymbol{A} = \boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{-1} \] 和奇异值分解 \[ \boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{-1}, \] 下面回顾一下它们的核心内容：

• 对于任意矩阵 \(\mathbb{R}^{m \times n}\)，奇异值分解总是存在的。而特征值分解仅对方阵 \(\mathbb{R}^{n \times n}\) 有效，并且仅当我们能找到 \(\mathbb{R}^n\) 的特征向量的基时才存在。

• 特征值分解矩阵 \(\boldsymbol{P}\) 中的向量不一定是正交的，即基的变化不是简单的旋转和缩放。而另一方面，奇异值分解中矩阵 \(\boldsymbol{U}\) 和 \(\boldsymbol{V}\) 中的向量是正交的，因此它们确实表示旋转。

• 特征值分解和奇异值分解都是三个线性映射的组合：

  • 定义域的基变换；
  • 每个新基向量的缩放都是独立的，并从定义域映射到陪域；
  • 陪域的基变换。 特征值分解和奇异值分解的一个关键区别是，在奇异值分解中，定义域和陪域可以是不同维数的向量空间。

• 在奇异值分解中，左奇异向量矩阵 \(\boldsymbol{U}\) 和右奇异向量矩阵 \(\boldsymbol{V}\) 通常不是互逆的（它们在不同的向量空间中执行基变换）。在特征值分解中，基变化矩阵 \(\boldsymbol{U}\) 和 \(\boldsymbol{U}^{-1}\) 是互逆的。

• 在奇异值分解中，对角矩阵 \(\boldsymbol{\Sigma}\) 中的项都是实的、非负的，这对于特征值分解中的对角矩阵则不一定成立。

• 奇异值分解和特征值分解通过它们的投影关系密切相关：

  • \(\boldsymbol{A}\) 的左奇异向量是 \(\boldsymbol{A} \boldsymbol{A}^\top\) 的特征向量；
  • \(\boldsymbol{A}\) 的右奇异向量是 \(\boldsymbol{A}^\top \boldsymbol{A}\) 的特征向量；
  • \(\boldsymbol{A}\) 的非零奇异值是 \(\boldsymbol{A} \boldsymbol{A}^\top\) 和 \(\boldsymbol{A}^\top \boldsymbol{A}\) 的非零特征值的平方根。

• 对于对称矩阵 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\)，特征值分解和奇异值分解是相同的，这符合谱定理（定理 4.15）。

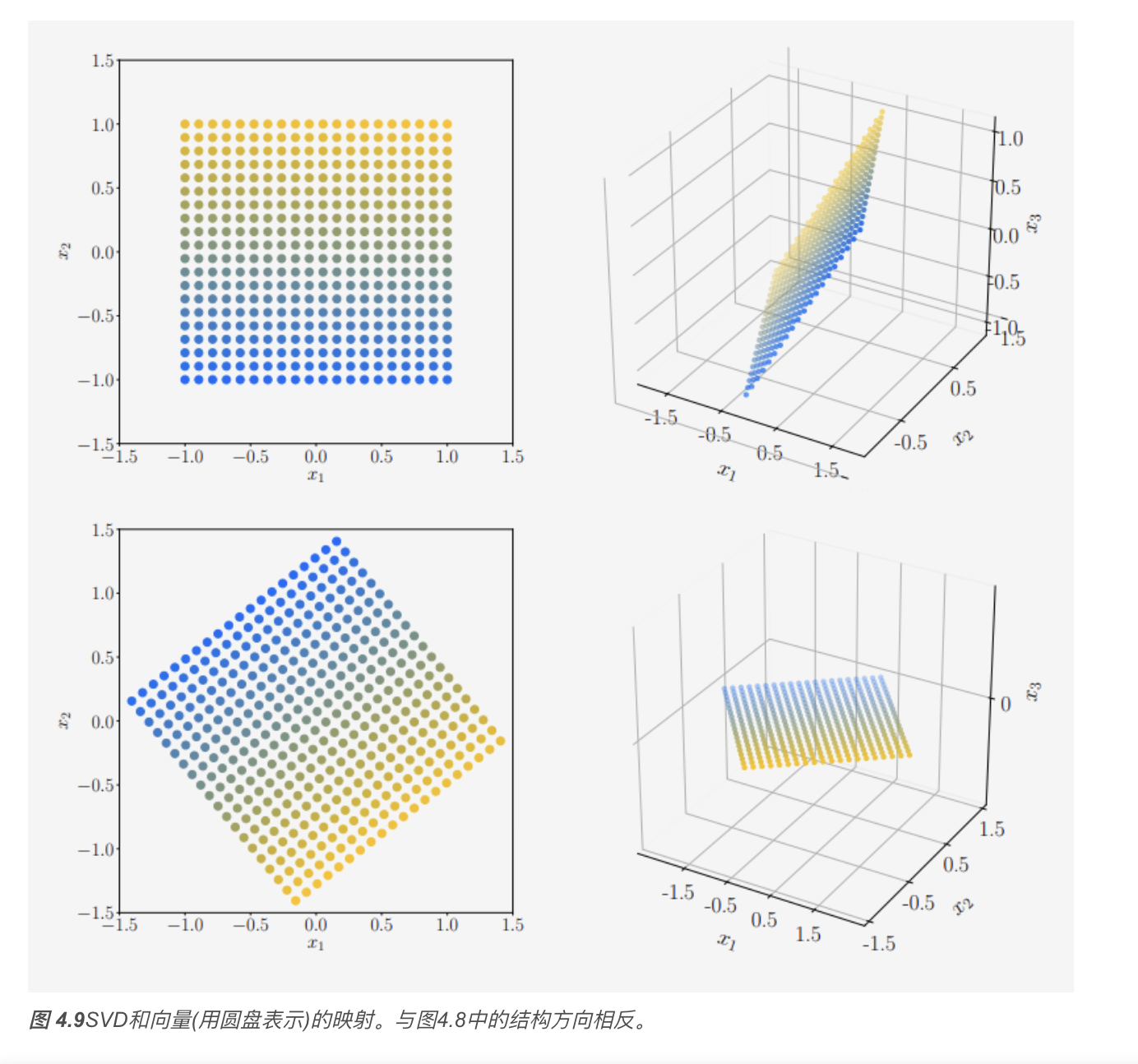
4.5.5 矩阵逼近

我们可以使用奇异值分解（SVD）将秩\(r\) 矩阵\(\boldsymbol{A}\)降为秩 \(k\) 矩阵 \(\widehat{\boldsymbol{A}}\) ，这是一种取主要成分并达到最优的（在谱范数意义上）方式。我们可以将秩\(k\)矩阵对\(\boldsymbol{A}\)的逼近解释为有损压缩的一种方法。因此，矩阵的低秩逼近出现在许多机器学习应用中，例如图像处理、噪声滤波和不适定问题的正则化。此外，它在降维和主成分分析中起着关键作用

秩为 \(r\) 的矩阵 \(\boldsymbol{A} \in \mathbb{R}^{m \times n}\) 能被写成秩 \(1\) 矩阵 \(\boldsymbol{A}_i\) 的和： \[ \boldsymbol{A} = \sum_{i=1}^{r} \sigma_{i} \boldsymbol{u}_{i} \boldsymbol{v}_{i}^{\top} = \sum_{i=1}^{r} \sigma_{i} \boldsymbol{A}_{i}, \] 其中，外积矩阵 \(\boldsymbol{A}_{i}\) 的权重为第 \(i\) 个奇异值 \(\sigma_{i}\)。

4.6 矩阵分类关系图

Matrix Phylogeny

可对角化其实就是可特征值分解。

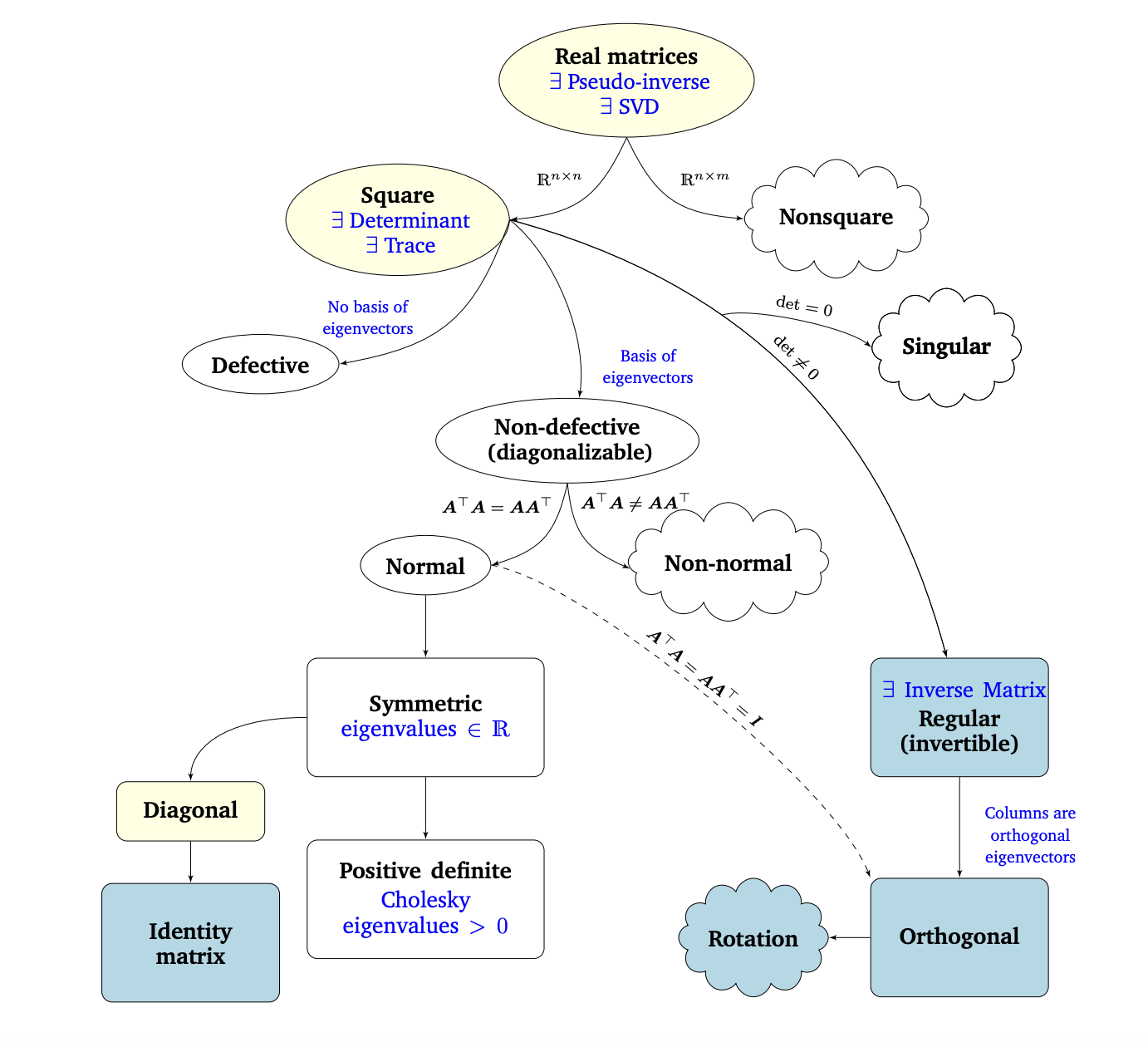
注：英文对应的中文翻译见文后。

在第2章和第3章中，我们介绍了线性代数和解析几何的基础知识。在这一章中，我们研究了矩阵和线性映射的基本特征。图4.13描述了不同类型矩阵之间关系的 Phylogeny（黑色箭头表示子集）以及我们可以对其执行的操作（蓝色）。

我们考虑所有实矩阵（real matrices）\(\boldsymbol{A} \in \mathbb{R}^{n \times m}\)。对于非方阵（其中 \(n \neq m\)），奇异值分解总是存在的，正如我们在本章中看到的。以方阵（square matrices）\(\boldsymbol{A} \in \mathbb{R}^{n \times n}\) 为中心，行列式告诉我们方阵是否具有逆矩阵（inverse matrix），即它是否属于正则可逆矩阵类。如果 \(n \times n\) 矩阵具有 \(n\) 个线性无关的特征向量，则矩阵是非退化的（non-defective），并且存在特征值分解（定理4.12）。我们知道，重复的特征值可能导致矩阵退化，这种矩阵是不能对角化的。

非奇异矩阵和非退化矩阵是不同的。例如，旋转矩阵是可逆的（行列式是非零的），但不一定可对角化（特征值不能保证是实数）。例子详见《非奇异矩阵和非退化矩阵.md》

我们进一步研究了非退化 \(n \times n\) 方阵的分支。如果条件\(\boldsymbol{A}^{\top} \boldsymbol{A} = \boldsymbol{A} \boldsymbol{A}^{\top}\)成立，则 \(\boldsymbol{A}\) 是正规的（normal）。此外，如果更严格的条件\(\boldsymbol{A}^{\top} \boldsymbol{A} = \boldsymbol{A} \boldsymbol{A}^{\top} = \boldsymbol{I}\)成立，则 \(\boldsymbol{A}\) 称为正交（orthogonal，见定义3.8）。正交矩阵集是正则（可逆）矩阵的子集，满足\(\boldsymbol{A}^{\top} = \boldsymbol{A}^{-1}.\)

正规矩阵有一个常见的子集，即对称矩阵 \(\boldsymbol{S} \in \mathbb{R}^{n \times n}\)，它满足\(\boldsymbol{S} = \boldsymbol{S}^{\top}.\)对称矩阵只有实特征值。对称矩阵的子集由正定矩阵 \(\boldsymbol{P}\) 组成，正定矩阵 \(\boldsymbol{P}\) 对所有 \(\boldsymbol{x} \in \mathbb{R}^{n} \backslash \{\mathbf{0}\}\) 满足条件\(\boldsymbol{x}^{\top} \boldsymbol{P} \boldsymbol{x} > 0.\)在这种情况下，存在唯一的 Cholesky 分解（Cholesky decomposition，定理4.18）。正定矩阵只有正特征值且总是可逆的（即，具有非零行列式）。

对称矩阵的另一个子集由对角矩阵（diagonal matrices）\(\boldsymbol{D}\) 组成。对角矩阵在乘法和加法下是闭合的，但不一定形成一个群（只有当所有的对角项都不为零时才是这种情况，这样矩阵才是可逆的）。一种特殊的对角矩阵是单位矩阵 \(\boldsymbol{I}\)。

常见矩阵分解总结表

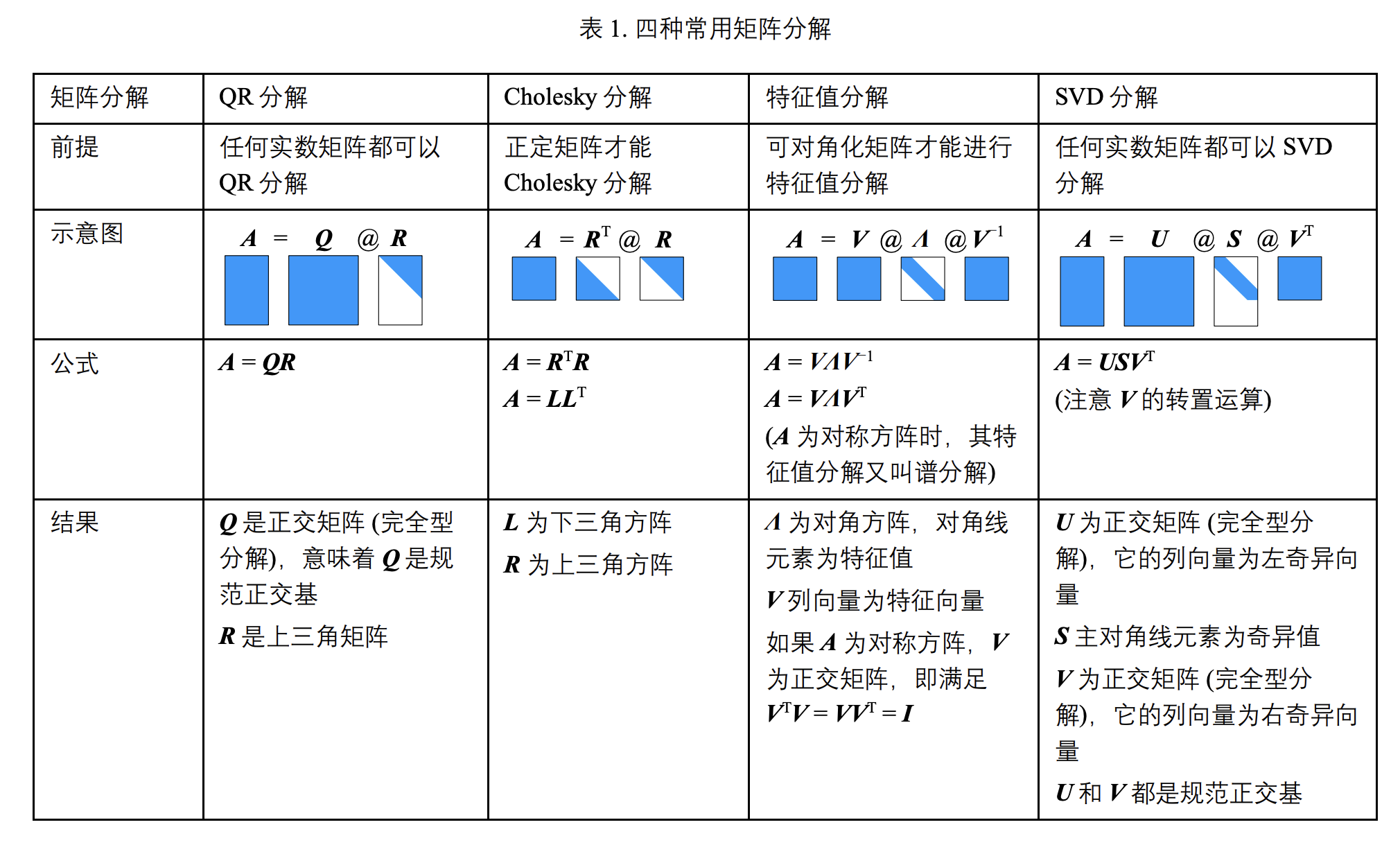
上表来源《鸢尾花套书》Book4_ch24 “矩阵力量”

矩阵分类关系图的英文翻译：

English	中文	说明（可选）
No basis of eigenvectors	特征向量不是基	不可对角化
Basis of eigenvectors	特征向量是基	可对角化
Singular	奇异的	\(\det=0\) ，不可逆
Regular	正则的	可逆矩阵
Defective	退化的	不具备完备特征向量组
Square	方阵	行数 = 列数
Normal	正规的	\(A^TA = AA^T\)
Symmetric	对称的	\(A = A^T\)
Diagonal	对角的	主对角线以外全是0
Identity matrix	单位矩阵	\(I\)
Orthogonal	正交的	\(A^TA = I\)
Rotation	旋转矩阵	正交且 $ =+1$
Positive definite	正定的	特征值 > 0
Eigenvalues	特征值	—

全书的读书笔记（共7篇）如下：
《机器学习的数学基础》读书笔记之一 ：导言
《机器学习的数学基础》读书笔记之二 ：线性代数
《机器学习的数学基础》读书笔记之三 ：解析几何
《机器学习的数学基础》读书笔记之四 ：矩阵分解
《机器学习的数学基础》读书笔记之五 ：向量微积分
《机器学习的数学基础》读书笔记之六 ：概率与分布
《机器学习的数学基础》读书笔记之七 ：连续优化