《机器学习的数学基础》（5/7）

5、向量微积分

Vector Calculus

函数的梯度方向指向最陡峭的上升方向，而不是导数本身。导数是标量，没有方向性；梯度才是决定函数与曲面上升方向的向量。理解这一点有助于区分函数与其图像（曲面）之间的关系。详见《导数和梯度的概念.md》

5.1 泰勒级数

泰勒级数是函数\(f\)的无穷项和的表示。这些项是用\(f\)的导数来确定的。多项式逼近函数的泰勒级数。

泰勒级数

对于一个平滑的函数 $ f ^{},  f: $ （$ f ^{} $ 表示 \(f\) 连续且可微无穷多次）， \(f\) 在 \(x_0\) 的泰勒级数(Taylor series）定义为：
\[ T_{\infty}(x) = \sum_{k=0}^{\infty} \frac{f^{(k)}\left(x_{0}\right)}{k !} \left(x - x_{0}\right)^{k} \]

当 $ x_0 = 0 $ 时，我们得到麦克劳林级数（Maclaurin series），它是泰勒级数的特殊实例。 如果 $ f(x) = T_{}(x) $，那么 \(f\) 称为解析的（analytic）。

泰勒级数中的 \(x_0\)（也叫展开点）原则上可以选任意实数或复数，不过能不能用它准确表示函数，还得看收敛性和函数的可导性条件。

注1： 一般来说，$ n $ 次泰勒多项式是非多项式函数的近似值。 它在 \(x_0\) 附近与 \(f\) 相似。 然而，$ n $ 次泰勒多项式用 $ k n $ 次多项式表示 \(f\) 已经足够精确了， 因为导数 $ f^{(i)},  i > k $ 可能为 \(0\)。

注2： 泰勒级数是幂级数的特例，幂级数表达式为：
\[ f(x) = \sum_{k=0}^{\infty} a_{k} (x - c)^{k} \] 其中 \(a_k\)为系数，\(c\)为常数。定义5.4中的式子是它的特殊形式。

注3：组合符号 \(C_n^m\) 也可写成 \(\binom{n}{m}\)。

5.2 微分法则

下面，我们用 $ f' $ 表示 \(f\) 的导数，简要地说明基本的微分规则：

1. 乘积法则：

\[ (f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \]

2. 除法法则：

\[ \left(\frac{f(x)}{g(x)}\right)' = \frac{f'(x) g(x) - f(x) g'(x)}{\left(g(x)\right)^{2}} \]

3. 加法法则：

\[ (f(x) + g(x))' = f'(x) + g'(x) \]

4. 链式法则：

\[ (g(f(x)))' = (g \circ f)'(x) = g'(f(x)) \cdot f'(x) \]

​ 这里，$ g f $ 表示函数复合：
\[ x \mapsto f(x) \mapsto g(f(x)) \]

5.3 偏微分与梯度

导数对多变量函数的推广是梯度(gradient)。

我们通过一次改变一个变量并保持其他变量不变来求函数\(f\)相对于\(x\)的偏导数。梯度就是这些偏导数(partial derivatives)构成的的集合。

将它们组成一个行向量： \[ \nabla_{\boldsymbol{x}} f = \operatorname{grad} f = \frac{\mathrm{d} f}{\mathrm{d} \boldsymbol{x}} = \left[ \frac{\partial f(\boldsymbol{x})}{\partial x_{1}},\ \frac{\partial f(\boldsymbol{x})}{\partial x_{2}},\ \cdots,\ \frac{\partial f(\boldsymbol{x})}{\partial x_{n}} \right] \in \mathbb{R}^{1 \times n} \qquad (5.40) \]

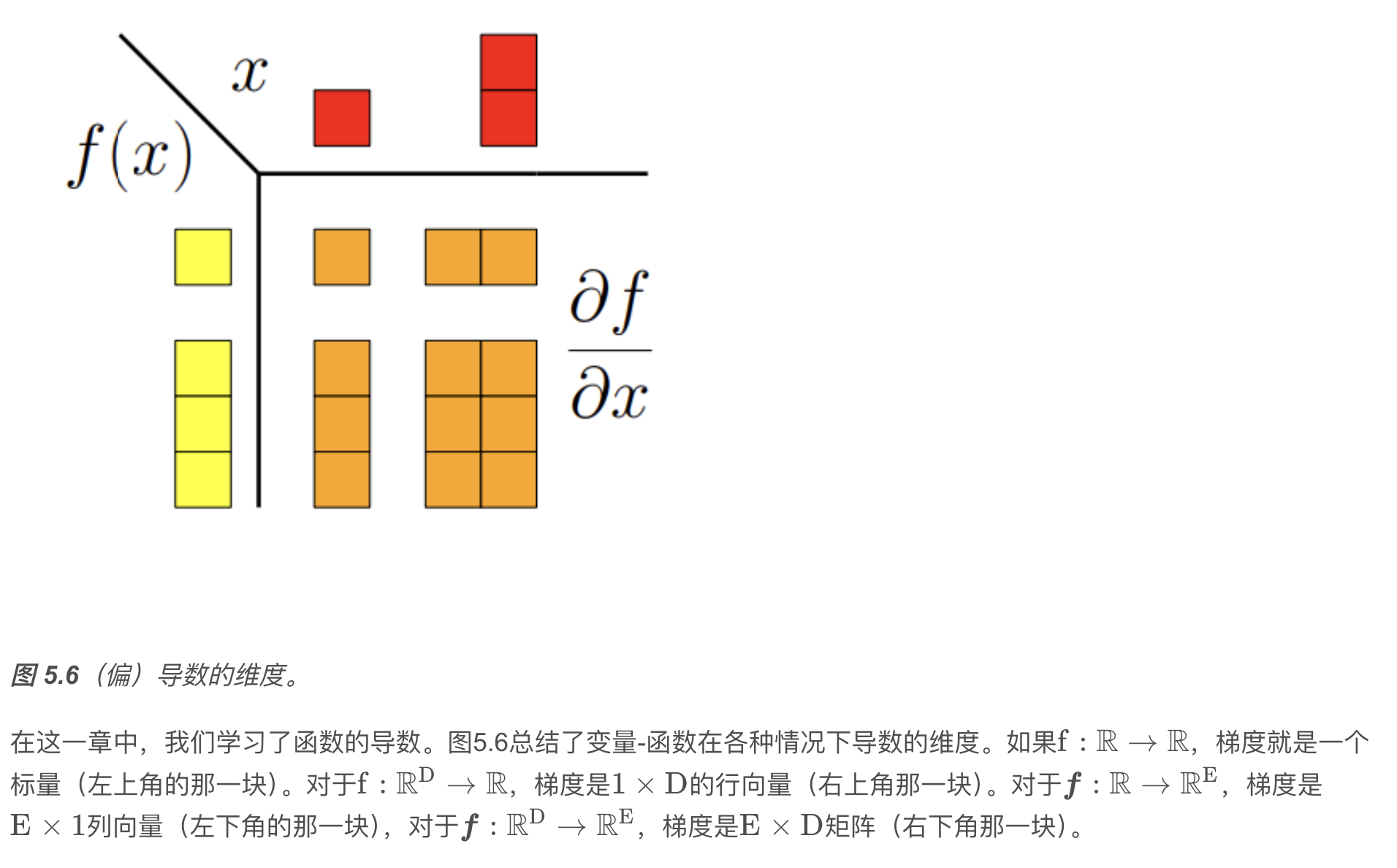
其中 $ n $ 是变量个数，\(1\) 是 \(f\) 的像/值域/陪域的维数。 这里，我们定义了列向量\(\boldsymbol{x} = \left[ x_{1}, \ldots, x_{n} \right]^{\top} \in \mathbb{R}^n.\) 式 (5.40) 中的行向量称为 \(f\) 的梯度(gradient) 或 雅可比矩阵(Jacobian)，是第 5.1 节中导数的推广。

备注（梯度用行向量表示）：

向量通常用列向量表示，将梯度向量定义为列向量在文献中并不少见。 我们将梯度向量定义为行向量的原因有两个： 首先，我们可以一致地将梯度推广到向量值函数\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\)（然后梯度变成矩阵）。 其次，我们可以很方便地应用多变量链式法则，而不必注意梯度的维数。

5.3.1 链式法则

考虑两个变量 \(x_{1}\), \(x_{2}\) 的函数\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}.\)此外，\(x_{1}(t)\) 和 \(x_{2}(t)\) 本身就是 \(t\) 的函数。 为了计算 \(f\) 相对于 \(t\) 的导数，我们需要对多元函数使用链式法则： \[ \frac{\mathrm{d} f}{\mathrm{d} t} = \begin{bmatrix} \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}} \end{bmatrix} \begin{bmatrix} \frac{\partial x_{1}(t)}{\partial t} \\ \frac{\partial x_{2}(t)}{\partial t} \end{bmatrix} = \frac{\partial f}{\partial x_{1}} \frac{\partial x_{1}}{\partial t} + \frac{\partial f}{\partial x_{2}} \frac{\partial x_{2}}{\partial t}. \] 其中 \(\mathrm{d}\) 表示全导数，\(\partial\) 表示偏导数。

5.3.2 多变量链式法则

如果 \(f(x_{1}, x_{2})\) 是 \(x_{1}\) 和 \(x_{2}\) 的函数，其中 \(x_{1}(s, t)\) 和 \(x_{2}(s, t)\) 是两个变量 \(s\) 和 \(t\) 的函数，则用链式法则可得偏导数： \[ \frac{\partial f}{\partial s} = \frac{\partial f}{\partial x_{1}} \frac{\partial x_{1}}{\partial s} + \frac{\partial f}{\partial x_{2}} \frac{\partial x_{2}}{\partial s}, \]

\[ \frac{\partial f}{\partial t} = \frac{\partial f}{\partial x_{1}} \frac{\partial x_{1}}{\partial t} + \frac{\partial f}{\partial x_{2}} \frac{\partial x_{2}}{\partial t}. \]

将梯度写成矩阵乘法的形式为： \[ \frac{\mathrm{d} f}{\mathrm{d}(s, t)} = \frac{\partial f}{\partial \boldsymbol{x}} \frac{\partial \boldsymbol{x}}{\partial (s, t)} = \underbrace{ \begin{bmatrix} \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}} \end{bmatrix} }_{\frac{\partial f}{\partial \boldsymbol{x}}} \underbrace{ \begin{bmatrix} \frac{\partial x_{1}}{\partial s} & \frac{\partial x_{1}}{\partial t} \\ \frac{\partial x_{2}}{\partial s} & \frac{\partial x_{2}}{\partial t} \end{bmatrix} }_{\frac{\partial \boldsymbol{x}}{\partial (s, t)}}. \]

这种将链式法则写成矩阵乘法的简洁方法，只有在将梯度定义为行向量时才直接成立。否则，需要对矩阵进行转置以匹配维数。当对象是向量或矩阵时，转置很简单；但当对象是张量时（将在后面讨论），转置就不再是小事了。

5.4 向量值函数的梯度

雅可比矩阵

向量值函数的所有一阶偏导数的集合称为雅可比矩阵（Jacobian）。雅可比矩阵 \(\mathbf{J}\) 是一个 \(m \times n\) 矩阵，我们将其定义如下： \[ \mathbf{J} = \nabla_{\mathbf{x}} \mathbf{f} = \frac{\mathrm{d} \mathbf{f}(\mathbf{x})}{\mathrm{d} \mathbf{x}} = \left[ \frac{\partial \mathbf{f}(\mathbf{x})}{\partial x_{1}} \quad \cdots \quad \frac{\partial \mathbf{f}(\mathbf{x})}{\partial x_{n}} \right]. \]

具体写成矩阵形式为： \[ \begin{equation} \mathbf{J} = \begin{bmatrix} \dfrac{\partial f_{1}(\mathbf{x})}{\partial x_{1}} & \cdots & \dfrac{\partial f_{1}(\mathbf{x})}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \dfrac{\partial f_{m}(\mathbf{x})}{\partial x_{1}} & \cdots & \dfrac{\partial f_{m}(\mathbf{x})}{\partial x_{n}} \end{bmatrix}, \tag{5.58} \end{equation} \] 其中 \[ \mathbf{x} = \begin{bmatrix} x_{1} \\ \vdots \\ x_{n} \end{bmatrix}, \quad J(i,j) = \frac{\partial f_{i}}{\partial x_{j}}. \]

雅可比矩阵表示我们想要的坐标变换。如果坐标变换是线性的（如我们的例子），那么它是精确的，（5.66）精确地恢复了（5.62）中的基变化矩阵。如果坐标变换是非线性的，雅可比矩阵则用一个线性变换局部地逼近这个非线性变换。雅可比行列式 \(|\operatorname{det}(\boldsymbol{J})|\) 的绝对值是变换坐标时面积或体积的缩放因子。

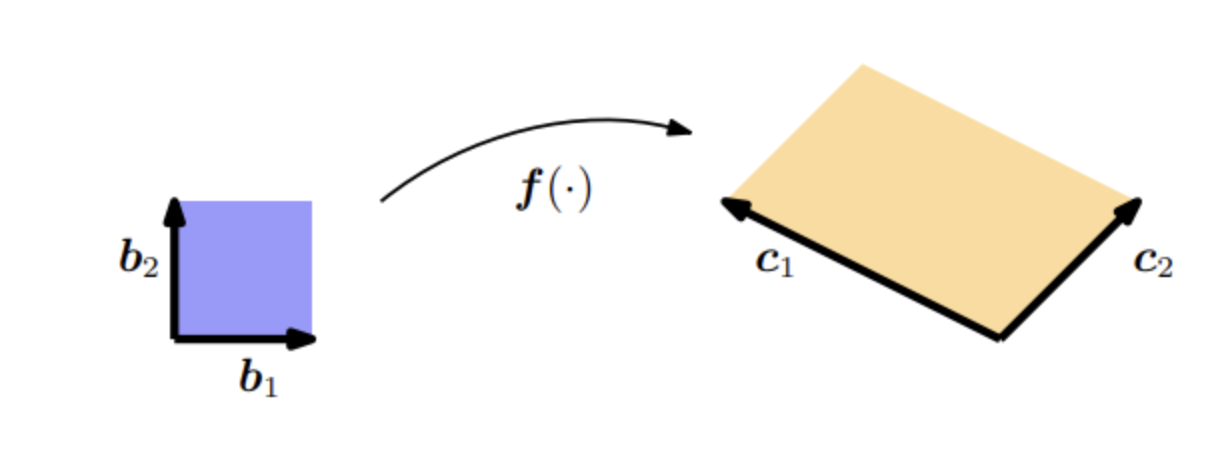
方法一、

为了开始使用线性代数的方法，我们首先确定 \(\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}\) 和 \(\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}\) 都是 \(\mathbb{R}^2\) 的基。我们要有效地执行的是从 \(\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}\) 到 \(\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}\) 的基变换，就得寻找实现基变换的变换矩阵。 利用第2.7.2节的结果，我们确定了所需的基变换矩阵为： \[ \boldsymbol{J} = \begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix} \tag{5.62} \]

它使得 \(\boldsymbol{J}\boldsymbol{b}_{1} = \boldsymbol{c}_{1}, \quad \boldsymbol{J}\boldsymbol{b}_{2} = \boldsymbol{c}_{2}\)。 矩阵 \(\boldsymbol{J}\) 的行列式的绝对值为： \[ \left|\det(\boldsymbol{J})\right| = 3, \] 这正是我们在寻找的缩放因子。也就是说， \((\boldsymbol{c}_{1}, \boldsymbol{c}_{2})\) 所张成的平行四边形的面积是 \((\boldsymbol{b}_{1}, \boldsymbol{b}_{2})\) 所张成面积的三倍。

把 \(\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}\) 坐标变换成 \(\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}\) 的坐标，是左乘\(\boldsymbol{J}^{-1}\)；反向是左乘\(\boldsymbol{J}\)。

方法二、

线性代数方法适用于线性变换；对于非线性变换（与第6.7节有关），我们有基于偏微分的更一般的方法。

在这种方法中，我们考虑执行变量变换的函数\(\boldsymbol{f}: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}.\)在我们的例子中，\(\boldsymbol{f}\) 将关于 \((\boldsymbol{b}_{1}, \boldsymbol{b}_{2})\) 的任意向量 \(\boldsymbol{x} \in \mathbb{R}^{2}\) 的坐标映射到关于 \((\boldsymbol{c}_{1}, \boldsymbol{c}_{2})\) 的坐标 \(\boldsymbol{y} \in \mathbb{R}^{2}\)。 我们想确定这个映射，这样就可以计算出一个面积（或体积）在 \(\boldsymbol{f}\) 变换下是如何变化的。 为此，我们需要找出 \(\boldsymbol{f}(\boldsymbol{x})\) 在 \(\boldsymbol{x}\) 微小变化时的变化方式。 雅可比矩阵 \[ \frac{\mathrm{d} \boldsymbol{f}}{\mathrm{d} \boldsymbol{x}} \in \mathbb{R}^{2 \times 2} \] 正是这个问题的答案。 由下式定义的映射： \[ y_{1} = -2x_{1} + x_{2}, \qquad y_{2} = x_{1} + x_{2}, \] 我们得到了 \(\boldsymbol{x}\) 和 \(\boldsymbol{y}\) 之间的函数关系。 这允许我们计算偏导数： \[ \frac{\partial y_{1}}{\partial x_{1}}=-2, \quad \frac{\partial y_{1}}{\partial x_{2}}=1, \quad \frac{\partial y_{2}}{\partial x_{1}}=1, \quad \frac{\partial y_{2}}{\partial x_{2}}=1. \]

将它们组合成雅可比矩阵： \[ \boldsymbol{J} = \begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} \\ \frac{\partial y_{2}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{2}} \end{bmatrix} = \begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix} \tag{5.66} \]

雅可比矩阵表示我们想要的坐标变换。 如果坐标变换是线性的（如我们的例子），那么它是精确的，（5.66）正好恢复了（5.62）中的基变化矩阵。 如果坐标变换是非线性的，雅可比矩阵则用一个线性变换局部地逼近这个非线性变换。 雅可比行列式的绝对值 \[ \left|\det(\boldsymbol{J})\right| = 3 \] 就是变换坐标时面积或体积的缩放因子。在我们的例子中，结果正好是 3。

向量值函数的梯度

给定： \[ \mathbf{f}(\mathbf{x}) = \mathbf{A} \mathbf{x} \] 其中：

• \(\mathbf{f}(\mathbf{x}) \in \mathbb{R}^M\)（输出是 \(M\) 维向量）
• \(\mathbf{A} \in \mathbb{R}^{M \times N}\)
• \(\mathbf{x} \in \mathbb{R}^N\)

这是一个线性映射：\(\mathbf{x} \mapsto \mathbf{A} \mathbf{x}\)。

向量值函数的梯度是 \(A\)。

5.4.1 反向传播与自动微分法

在许多机器学习应用中，我们通过执行梯度下降（第7.1节）来找到好的模型参数，这基于我们可以计算目标函数相对于模型参数的梯度。对于给定的目标函数，我们可以通过微积分和应用链式法则来获得关于模型参数的梯度；见第5.2.2节。在第5.3节中，我们已经研究了线性回归模型的平方损失函数的梯度。

反向传播是数值分析中称为自动微分(automatic differentiation)技术的一个特例。我们可以把自动微分看作是一套技术，它通过处理中间变量和应用链式法则，在数值上（而不是符号化地）计算函数的精确（达到机器精度）梯度。自动微分应用了一系列基本算术运算，例如加法和乘法，以及基本函数，例如：\(⁡ \sin , \cos , \exp , \log\)将链式法则应用到这些运算中，可以自动计算相当复杂函数的梯度。自动微分适用于一般的计算机程序，有正向和反向两种模式。

直观地说，正向和反向模式在乘法的顺序上是不同的。由于矩阵乘法的结合性，我们有以下两种选择： \[ \begin{equation} \frac{\mathrm{d} y}{\mathrm{d} x} = \left( \frac{\mathrm{d} y}{\mathrm{d} b} \frac{\mathrm{d} b}{\mathrm{d} a} \right) \frac{\mathrm{d} a}{\mathrm{d} x} \qquad (5.120) \end{equation} \]

\[ \begin{equation} \frac{\mathrm{d} y}{\mathrm{d} x} = \frac{\mathrm{d} y}{\mathrm{d} b} \left( \frac{\mathrm{d} b}{\mathrm{d} a} \frac{\mathrm{d} a}{\mathrm{d} x} \right) \qquad (5.121) \end{equation} \]

方程（5.120）是反向模式（reverse mode），因为梯度通过数据流向后传播。 方程（5.121）是正向模式（forward mode），其中梯度随数据从左到右流过整个图。

下面，我们将重点介绍反向模式的自动微分，即反向传播。

在神经网络中，输入的维数通常比标签的维数高得多，所以反向模式比正向模式计算量要少得多。

具体的例子详见《损失函数的梯度计算例子.md》

全书的读书笔记（共7篇）如下：
《机器学习的数学基础》读书笔记之一 ：导言
《机器学习的数学基础》读书笔记之二 ：线性代数
《机器学习的数学基础》读书笔记之三 ：解析几何
《机器学习的数学基础》读书笔记之四 ：矩阵分解
《机器学习的数学基础》读书笔记之五 ：向量微积分
《机器学习的数学基础》读书笔记之六 ：概率与分布
《机器学习的数学基础》读书笔记之七 ：连续优化