第7章无监督学习

发表于 2025-09-25 分类于读书心得

《Practical Statistics for Data Scientists》书籍英文版
 《面向数据科学家的实用统计学》中文版书籍

第7章无监督学习

Unsupervised Learning

无监督学习这个术语指的是在没有标注数据（即已知感兴趣结果的数据）的情况下，从数据中提取意义的统计方法。在第四章到第六章中，目标是构建一个模型（一套规则），用一组预测变量来预测一个响应变量。这就是监督学习。与此相反，无监督学习也构建数据的模型，但它不区分响应变量和预测变量。

无监督学习可以用于实现不同的目标。在某些情况下，当没有带标签的响应变量时，它可用于创建预测规则。例如，聚类方法可以用于识别有意义的数据组。我们可以使用用户在网站上的点击和人口统计数据，将不同类型的用户分组。然后，网站可以根据这些不同类型进行个性化。

在另一些情况下，目标可能是将数据的维度降至一个更易于管理的变量集。然后，这个缩减后的集合可以作为输入用于预测模型，比如回归或分类。例如，我们可能有成千上万个传感器来监测一个工业过程。通过将数据简化为一个更小的特征集，我们也许能够构建一个比包含数千个传感器数据流更强大、更可解释的过程故障预测模型。

最后，无监督学习可以被视为探索性数据分析（参见第一章）的延伸，适用于您面对大量变量和记录的情况。其目的是深入了解一组数据以及不同变量之间的相互关系。无监督技术让您能够筛选和分析这些变量，并发现其中的关系。

通用注解：

无监督学习与预测（Unsupervised Learning and Prediction）

无监督学习在预测中可以扮演重要角色，无论是对于回归还是分类问题。在某些情况下，我们想在没有任何标注数据的情况下预测一个类别。例如，我们可能想根据一组卫星传感器数据来预测某个区域的植被类型。由于我们没有响应变量来训练模型，聚类为我们提供了一种识别常见模式并对区域进行分类的方法。

聚类是解决“冷启动问题”（cold-start problem）的一个特别重要的工具。在这种类型的问题中，例如发起一项新的营销活动或识别潜在的新型欺诈或垃圾邮件，我们最初可能没有任何响应变量来训练模型。随着时间的推移，当数据被收集起来后，我们可以更多地了解该系统并构建一个传统的预测模型。但聚类通过识别人口细分来帮助我们更快地启动学习过程。

无监督学习作为回归和分类技术的构建模块也很重要。对于大数据，如果一个小的子群体在整体群体中没有得到很好的代表，那么训练出的模型在该子群体上的表现可能不佳。通过聚类，可以识别并标记这些子群体。然后，可以为不同的子群体分别拟合单独的模型。或者，子群体可以用其自身的特征来表示，迫使整体模型明确地将子群体身份作为预测变量来考虑。

主成分分析

Principal Components Analysis

通常，变量会共同变化（协变），其中一个变量的某些变异实际上被另一个变量的变异所重复（例如，餐馆账单和给的小费）。主成分分析（PCA）是一种用于发现数值变量如何协变的技术。

主成分分析的关键术语

主成分（Principal component） 预测变量的线性组合。
载荷（Loadings） 将预测变量转换为成分的权重。同义词：权重（Weights）
碎石图（Screeplot） 成分方差图，显示了成分的相对重要性，可以是解释方差或解释方差的比例。

PCA 的思想是将多个数值预测变量组合成一个更小的变量集，这些变量是原始变量集的加权线性组合。这个更小的变量集（即主成分）“解释”了大部分原始变量集的变异性，从而降低了数据的维度。用于形成主成分的权重揭示了原始变量对新主成分的相对贡献。

PCA 最初由卡尔·皮尔逊提出。在一篇可能是关于无监督学习的开创性论文中，皮尔逊认识到在许多问题中，预测变量存在变异性，因此他开发了 PCA 作为一种对这种变异性进行建模的技术。PCA 可以被看作是线性判别分析的无监督版本；参见第201页的“判别分析”。

一个简单的例子

对于两个变量 $X_1$ 和 $X_2$，有两个主成分 $Z_i$（$i=1$ 或 $2$）：

\[ Z_i = w_{i,1}X_1 + w_{i,2}X_2 \] 权重 $w_{i,1}, w_{i,2}$ 被称为成分载荷。这些载荷将原始变量转换为主成分。第一个主成分 $Z_1$ 是最能解释总变异性（variation）的线性组合。第二个主成分 $Z_2$ 与第一个正交，并尽可能多地解释剩余的变异性。（如果还有额外的成分，每个新增的成分都会与其他的正交。）

通用注解：

通常，也对偏离预测变量均值的偏差而不是对变量本身的值来计算主成分。

您可以使用 princomp 函数在 R 中计算主成分。以下代码对雪佛龙（CVX）和埃克森美孚（XOM）的股票价格回报进行了主成分分析（PCA）：

1
2
3

oil_px <- sp500_px[, c('CVX', 'XOM')]
pca <- princomp(oil_px)
pca$loadings

Loadings:
        Comp.1 Comp.2
CVX -0.747  0.665
XOM -0.665 -0.747

               Comp.1 Comp.2
SS loadings     1.0    1.0
Proportion Var  0.5    0.5
Cumulative Var  0.5    1.0

在 Python 中，我们可以使用 scikit-learn 实现 sklearn.decomposition.PCA：

pcs = PCA(n_components=2)
pcs.fit(oil_px)
loadings = pd.DataFrame(pcs.components_, columns=oil_px.columns)
loadings

第一个主成分的 CVX 和 XOM 权重分别为 -0.747 和 -0.665，第二个主成分的权重分别为 0.665 和 -0.747。这该如何解释呢？第一个主成分本质上是 CVX 和 XOM 的平均值，反映了这两家能源公司之间的相关性。第二个主成分则衡量了CVX 和 XOM 的股票价格何时出现分歧。

将主成分与数据一起绘制出来是很有启发性的。这里我们用 R 创建一个可视化图：

loadings <- pca$loadings
ggplot(data=oil_px, aes(x=CVX, y=XOM)) +
geom_point(alpha=.3) +
stat_ellipse(type='norm', level=.99) +
geom_abline(intercept = 0, slope = loadings[2,1]/loadings[1,1]) +
geom_abline(intercept = 0, slope = loadings[2,2]/loadings[1,2])

以下代码在 Python 中创建了一个类似的可视化图：

def abline(slope, intercept, ax):
    """Calculate coordinates of a line based on slope and intercept"""
    x_vals = np.array(ax.get_xlim())
    return (x_vals, intercept + slope * x_vals)
ax = oil_px.plot.scatter(x='XOM', y='CVX', alpha=0.3, figsize=(4, 4))
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
ax.plot(*abline(loadings.loc[0, 'CVX'] / loadings.loc[0, 'XOM'], 0, ax),
        '--'
        , color='C1')
ax.plot(*abline(loadings.loc[1, 'CVX'] / loadings.loc[1, 'XOM'], 0, ax),
        '--'
        , color='C1')

结果如图7-1所示。虚线显示了两个主成分的方向：第一个沿着椭圆的长轴，第二个沿着短轴。您可以看到，这两个股票回报的大部分变异性都由第一个主成分解释。这是有道理的，因为能源股价格倾向于作为一个群体移动。

F7.1

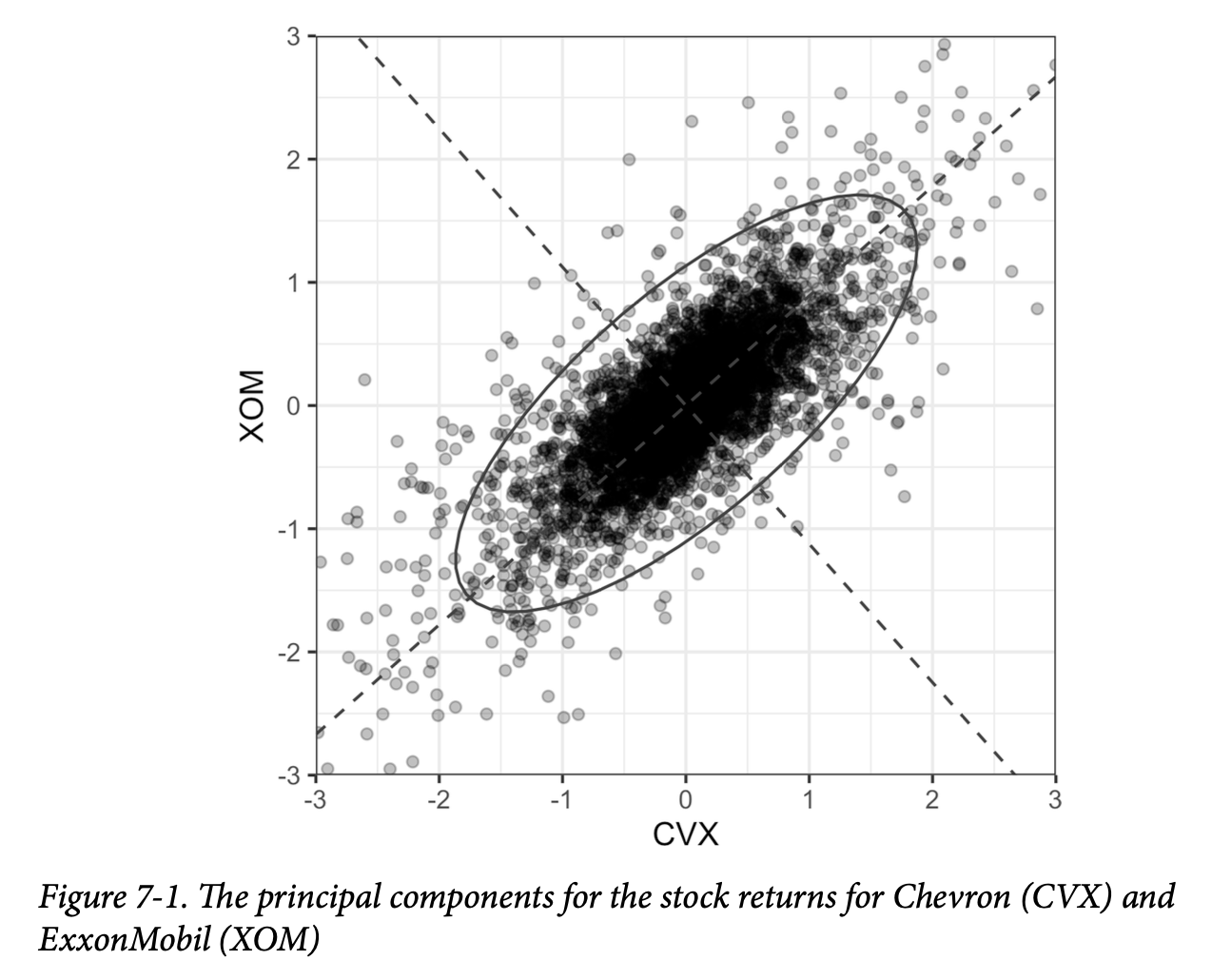
通用注解：

第一个主成分的权重都是负的，但将所有权重的符号反转并不会改变主成分。例如，对于第一个主成分，使用0.747和0.665的权重与使用负权重是等效的，就像由原点和(1,1)定义的无限线与由原点和(-1,-1)定义的线是同一条一样。

计算主成分

Computing the Principal Components

从两个变量扩展到更多变量是直接的。对于第一个成分，只需将额外的预测变量包含在线性组合中，并分配权重，以优化从所有预测变量中收集的协变（ the covariation from all the predictor variables）到这个第一个主成分中（协方差（covariance）是统计术语；参见第202页的“协方差矩阵”）。主成分的计算是一种经典的统计方法，它依赖于数据的相关矩阵或协方差矩阵，并且执行迅速，不依赖于迭代。如前所述，主成分分析仅适用于数值变量，不适用于分类变量。

完整的流程可以描述如下：

在创建第一个主成分时，PCA 得到的预测变量线性组合能最大化解释的总方差百分比。
这个线性组合随后成为第一个“新”预测变量 $Z_1$。
PCA 重复此过程，使用相同的变量但采用不同的权重，来创建第二个新预测变量 $Z_2$。权重的分配使得 $Z_1$ 和 $Z_2$ 不相关。
该过程持续进行，直到您拥有与原始变量 $X_i$ 一样多的新变量（或成分）$Z_i$。
选择保留足以解释大部分方差的成分数量。
到目前为止，结果是每个成分的一组权重。最后一步是通过将权重应用于原始值，将原始数据转换为新的主成分得分。这些新得分随后可以用作简化后的预测变量集。

解释主成分

Interpreting Principal Components

主成分的性质通常能揭示数据的结构信息。有几种标准的可视化方式可以帮助您深入了解主成分。其中一种方法是碎石图，用于可视化主成分的相对重要性（其名称源于该图与碎石坡的相似之处；这里的y轴是特征值）。以下 R 代码显示了标普500指数中几家顶尖公司的例子：

syms <- c( 'AAPL', 'MSFT', 'CSCO', 'INTC', 'CVX', 'XOM',
'SLB', 'COP', 'JPM', 'WFC', 'USB', 'AXP', 'WMT', 'TGT', 'HD', 'COST')
top_sp <- sp500_px[row.names(sp500_px)>='2005-01-01', syms]
sp_pca <- princomp(top_sp)
screeplot(sp_pca)

从 scikit-learn 的结果中创建加载图的信息可在 explained_variance_ 中获得。这里，我们将其转换为一个 pandas 数据框，并用它来制作一个条形图：

syms = sorted(['AAPL', 'MSFT', 'CSCO', 'INTC', 'CVX', 'XOM', 'SLB', 'COP',
'JPM', 'WFC', 'USB', 'AXP', 'WMT', 'TGT', 'HD', 'COST'])
top_sp = sp500_px.loc[sp500_px.index >= '2011-01-01', syms]
sp_pca = PCA()
sp_pca.fit(top_sp)
explained_variance = pd.DataFrame(sp_pca.explained_variance_)
ax = explained_variance.head(10).plot.bar(legend=False, figsize=(4, 4))
ax.set_xlabel('Component')

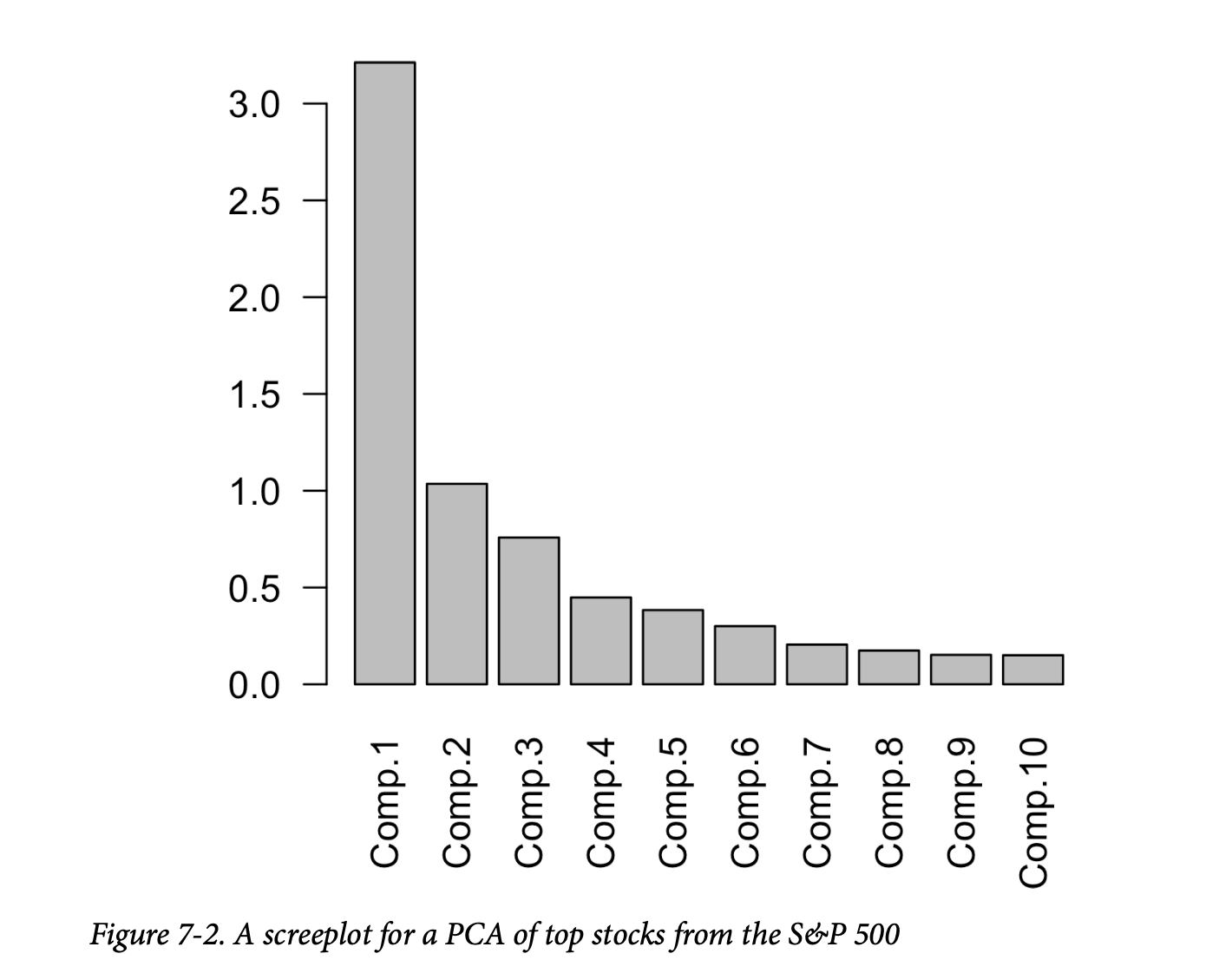
如图7-2所示，第一个主成分的方差相当大（通常如此），但其他靠前的主成分也具有显著性。

F7.2

通常，绘制顶层主成分的权重会非常有启发性。在 R 中，一种方法是结合使用 tidyr 包的 gather 函数和 ggplot：

library(tidyr)
loadings <- sp_pca$loadings[,1:5]
loadings$Symbol <- row.names(loadings)
loadings <- gather(loadings, 'Component', 'Weight',
ggplot(loadings, aes(x=Symbol, y=Weight)) +
geom_bar(stat='identity') +
facet_grid(Component ~
., scales='free_y')
-Symbol)

以下是用于在 Python 中创建相同可视化图的代码：

loadings = pd.DataFrame(sp_pca.components_[0:5, :], columns=top_sp.columns)
maxPC = 1.01 * np.max(np.max(np.abs(loadings.loc[0:5, :])))
f, axes = plt.subplots(5, 1, figsize=(5, 5), sharex=True)
for i, ax in enumerate(axes):
pc_loadings = loadings.loc[i, :]
colors = ['C0' if l > 0 else 'C1' for l in pc_loadings]
ax.axhline(color='#888888')

pc_loadings.plot.bar(ax=ax, color=colors)
ax.set_ylabel(f'PC{i+1}')
ax.set_ylim(-maxPC, maxPC)

F7.3

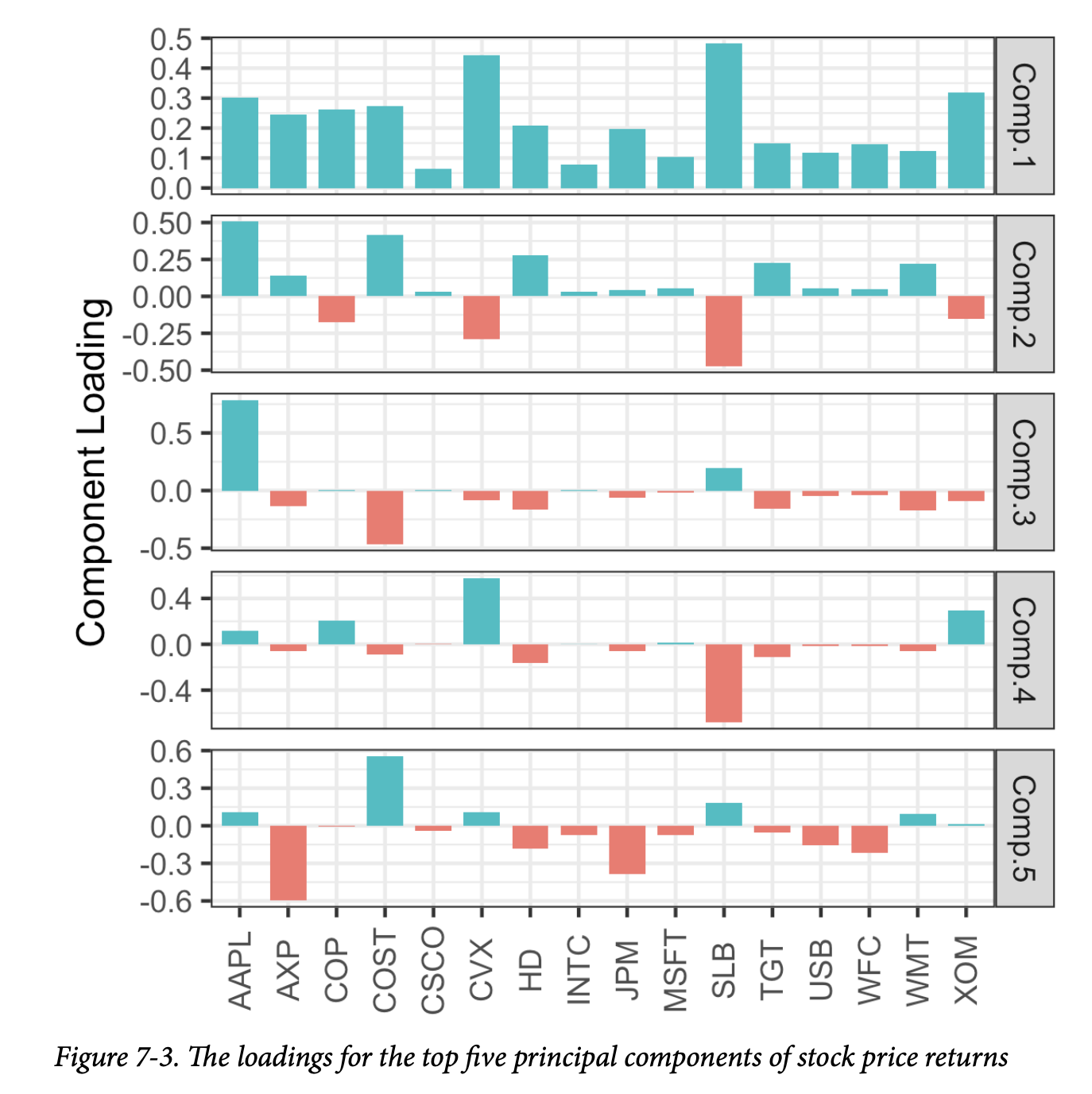
前五个成分的载荷如图7-3所示。

第一个主成分的载荷符号都相同：这对于所有列都共享一个共同因素（在本例中为整体股市趋势）的数据来说是很典型的。
第二个成分捕捉了能源股与其他股票相比的价格变化。
第三个成分主要是苹果和CostCo的走势对比。
第四个成分对比了斯伦贝谢（SLB）与其他能源股的走势。
最后，第五个成分主要由金融公司主导。

通用注解：如何选择成分数量？How Many Components to Choose? 如果您的目标是降低数据的维度，您必须决定选择多少个主成分。最常见的方法是使用临时规则来选择那些能够解释“大部分”方差的成分。您可以通过碎石图进行直观操作，例如在图7-2中所示。或者，您可以选择累积方差超过某个阈值（如80%）的顶层成分。您还可以检查载荷，以确定该成分是否具有直观的解释。交叉验证为选择显著成分的数量提供了一种更正式的方法（更多内容请参见第155页的“交叉验证”）。

对应分析

Correspondence Analysis

PCA不能用于分类数据；然而，有一种与其有所关联的技术是对应分析（Correspondence analysis）。其目标是识别类别之间或分类特征之间的关联。对应分析和主成分分析之间的相似之处主要在于底层——用于维度缩放的矩阵代数。对应分析主要用于低维分类数据的图形分析，不像 PCA 那样被用作大数据背景下的降维准备步骤。

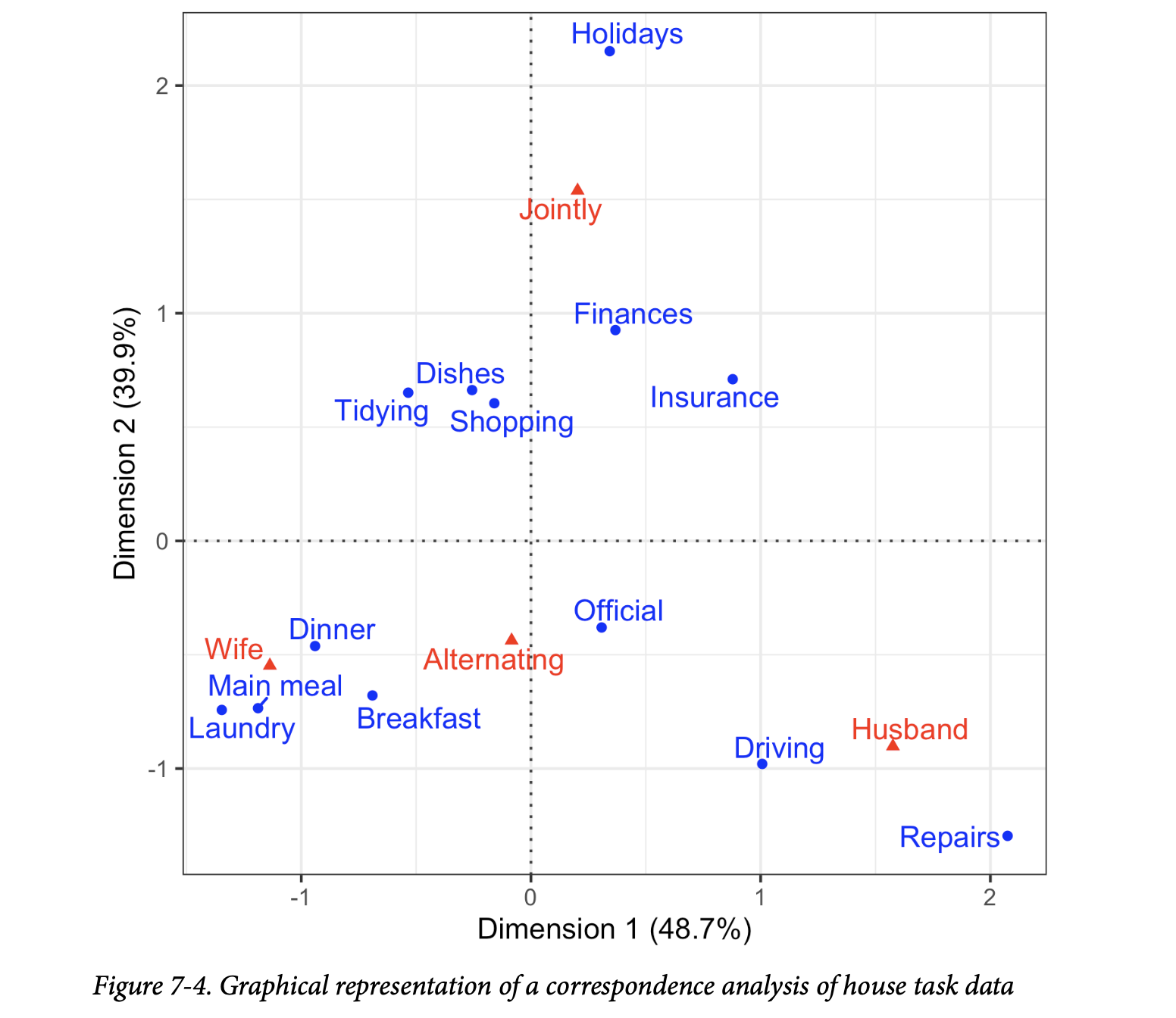
输入可以看作一个表格，其中行代表一个变量，列代表另一个变量，而单元格代表记录计数。输出（经过一些矩阵代数处理后）是一个双标图（biplot）——一个散点图，其坐标轴经过缩放（百分比表示该维度解释了多少方差）。坐标轴上单位的含义与原始数据没有直观的联系，散点图的主要价值在于以图形方式展示相互关联的变量（通过在图上的邻近性）。例如，参见图7-4，其中家务任务根据是共同完成还是单独完成（垂直轴）以及主要由妻子还是丈夫负责（水平轴）进行排列。从任务的分配来看，对应分析和这个示例的精神都已有数十年历史。

F7.4

R 中有多种用于对应分析的软件包。这里，我们使用 ca 包：

1 2	ca_analysis <- ca(housetasks) plot(ca_analysis)

在 Python 中，我们可以使用 prince 包，它使用 scikit-learn API 实现了对应分析：

1
2
3

ca = prince.CA(n_components=2)
ca = ca.fit(housetasks)
ca.plot_coordinates(housetasks, figsize=(6, 6))

关键思想

主成分是预测变量的线性组合（仅限数值数据）。
计算主成分是为了最小化成分之间的相关性，从而减少冗余。
数量有限的成分通常可以解释因变量的大部分方差。
这个有限的主成分集可以用来代替（数量更多的）原始预测变量，从而达到降维的目的。
一种表面上相似的分类数据技术是对应分析，但它在大数据环境中并不实用。

K-均值聚类

K-Means Clustering

聚类是一种将数据划分为不同组的技术，其中每组中的记录彼此相似。聚类的一个目标是识别重要且有意义的数据组。这些组可以直接使用，可以进行更深入的分析，或者作为特征或结果传递给预测性回归或分类模型。K-均值（K-means）是第一个被开发的聚类方法；由于其算法相对简单且能够扩展到大型数据集，它仍然被广泛使用。

个人注：K最近邻 (K-Nearest Neighbors, KNN) 和 K均值 (K-Means) 算法虽然名字里都带“K”，但它们在机器学习领域扮演着截然不同的角色。

KNN 是一个监督学习算法，主要用于分类或回归。它需要有标签的训练数据。

K均值 是一个无监督学习算法，主要用于聚类。它处理没有标签的数据。

简单来说，KNN 是用来预测新数据点的类别或值，而 K均值是用来发现数据中固有的分组。

K-均值聚类的关键术语

簇（Cluster） 一组彼此相似的记录。
簇均值（Cluster mean） 簇中记录的变量均值向量。
K 簇的数量。

K-均值通过最小化每条记录到其所属簇均值的平方距离总和来将数据划分为 $K$ 个簇。这被称为簇内平方和（within-cluster sum of squares）或簇内SS（within-cluster SS）。K-均值不保证簇的大小相同，但它会找到分隔度最佳的簇。

通用注解：标准化 Normalization

通常通过减去均值并除以标准差来对连续变量进行标准化（归一化）。否则，尺度较大的变量会主导聚类过程（参见第243页的“标准化（归一化、z-分数）”）。

一个简单的例子

从一个包含 $n$ 条记录和仅有两个变量 $x$ 和 $y$ 的数据集开始考虑。假设我们想将数据分为 $K = 4$ 个簇。这意味着将每条记录 $(x_i, y_i)$ 分配给一个簇 $k$。给定将 $n_k$ 条记录分配到簇 $k$ 的任务，该簇的中心 $(\bar{x}_k, \bar{y}_k)$ 是簇中所有点的均值：

簇均值： \[ \bar{x}_k = \frac{1}{n_k} \sum_{i \in \text{Cluster } k} x_i \] \[ \bar{y}_k = \frac{1}{n_k} \sum_{i \in \text{Cluster } k} y_i \]

警告：Cluster Mean 在对具有多个变量的记录进行聚类时（这是典型情况），簇均值这个术语指的不是一个单一的数字，而是变量均值的向量。

一个簇内的平方和由下式给出：

\[ SS_k = \sum_{i \in \text{Cluster } k} (x_i - \bar{x}_k)^2 + (y_i - \bar{y}_k)^2 \]

K-均值通过最小化所有四个簇的簇内平方和总和 $SS_1 + SS_2 + SS_3 + SS_4$ 来寻找记录的最佳分配：

\[ \sum_{k=1}^{4} SS_k \]

聚类的一个典型用途是定位数据中自然、分离的簇。另一个应用是将数据划分为预定数量的独立组，其中聚类用于确保这些组彼此尽可能地不同。

例如，假设我们想将每日股票回报分为四个组。K-均值聚类可用于将数据分离为最佳分组。请注意，每日股票回报的报告方式实际上是标准化的，因此我们不需要对数据进行归一化。在 R 中，K-均值聚类可以使用 kmeans 函数执行。例如，以下代码基于两个变量——埃克森美孚（XOM）和雪佛龙（CVX）的每日股票回报——寻找四个簇：

1 2	df <- sp500_px[row.names(sp500_px)>='2011-01-01', c('XOM', 'CVX')] km <- kmeans(df, centers=4)

在 Python 中，我们使用 scikit-learn 的 sklearn.cluster.KMeans 方法：

1 2	df = sp500_px.loc[sp500_px.index >= '2011-01-01', ['XOM', 'CVX']] kmeans = KMeans(n_clusters=4).fit(df)

每条记录的簇分配以 cluster 组件的形式返回（R）：

> df$cluster <- factor(km$cluster)
> head(df)
                  XOM        CVX cluster
2011-01-03 0.73680496 0.2406809 2
2011-01-04 0.16866845 -0.5845157 1
2011-01-05 0.02663055 0.4469854 2
2011-01-06 0.24855834 -0.9197513 1
2011-01-07 0.33732892 0.1805111 2
2011-01-10 0.00000000 -0.4641675 1

在 scikit-learn 中，簇标签在 labels_ 字段中可用：

1 2	df['cluster'] = kmeans.labels_ df.head()

前六条记录被分配到簇1或簇2。簇的均值也一并返回（R）：

> centers <- data.frame(cluster=factor(1:4), km$centers)
> centers
  cluster         XOM         CVX
1       1 -0.3284864 -0.5669135
2       2  0.2410159  0.3342130
3       3 -1.1439800 -1.7502975
4       4  0.9568628  1.3708892

在 scikit-learn 中，簇中心在 cluster_centers_ 字段中可用：

1 2	centers = pd.DataFrame(kmeans.cluster_centers_, columns=['XOM', 'CVX']) centers

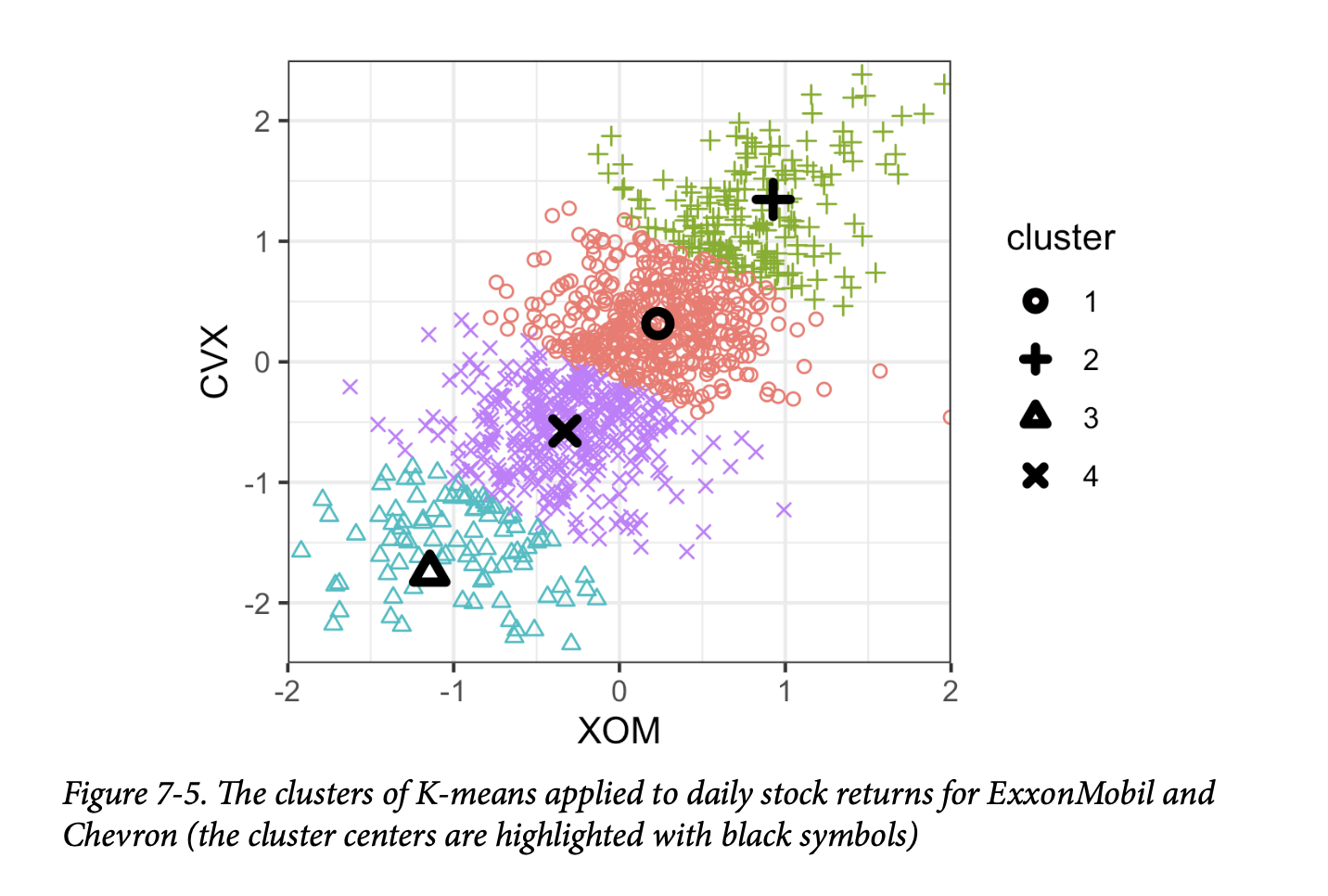
簇1和3代表“下行”市场，而簇2和4代表“上行”市场。

由于 K-均值算法使用随机起始点，因此后续的运行和不同的方法实现可能会产生不同的结果。一般来说，您应该检查波动是否不太大。

在这个只有两个变量的例子中，可视化簇及其均值是直截了当的：

1
2
3

ggplot(data=df, aes(x=XOM, y=CVX, color=cluster, shape=cluster)) +
geom_point(alpha=.3) +
geom_point(data=centers, aes(x=XOM, y=CVX), size=3, stroke=2)

seaborn 的 scatterplot 函数可以很容易地按属性对点进行颜色 (hue) 和样式 (style) 设置：

fig, ax = plt.subplots(figsize=(4, 4))
ax = sns.scatterplot(x='XOM', y='CVX', hue='cluster', style='cluster',
ax=ax, data=df)
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
centers.plot.scatter(x='XOM', y='CVX', ax=ax, s=50, color='black')

最终的图（如图7-5所示）显示了簇分配和簇均值。请注意，K-均值会将记录分配给簇，即使这些簇没有很好地分离（如果您需要将记录最佳地划分为多个组，这可能是有用的）。

F7.5

K-均值算法

K-Means Algorithm

通常，K-均值可以应用于具有 $p$ 个变量 $X_1, \dots, X_p$ 的数据集。虽然 K-均值的精确解在计算上非常困难，但启发式算法提供了一种有效的方式来计算局部最优解。

该算法从用户指定的 $K$ 值和一组初始簇均值开始，然后迭代以下步骤：

根据平方距离将每条记录分配给最近的簇均值。
根据记录的分配计算新的簇均值。

当记录到簇的分配不再变化时，算法收敛。对于第一次迭代，您需要指定一组初始簇均值。通常，您可以通过将每条记录随机分配给 $K$ 个簇中的一个，然后找到这些簇的均值来实现。

由于该算法不保证能找到最佳解决方案，因此建议使用不同的随机样本来初始化算法，并多次运行。当使用多组迭代时，K-均值的结果由簇内平方和最低的那次迭代给出。

R 函数 kmeans 的 nstart 参数允许您指定要尝试的随机起始点数量。例如，以下代码运行 K-均值以寻找5个簇，使用了10个不同的起始簇均值：

syms <- c( 'AAPL', 'MSFT', 'CSCO', 'INTC', 'CVX', 'XOM', 'SLB', 'COP',
'JPM', 'WFC', 'USB', 'AXP', 'WMT', 'TGT', 'HD', 'COST')
df <- sp500_px[row.names(sp500_px) >= '2011-01-01', syms]
km <- kmeans(df, centers=5, nstart=10)

该函数会自动返回10个不同起始点中的最佳解决方案。您可以使用 iter.max 参数来设置算法每次随机开始所允许的最大迭代次数。

scikit-learn 算法默认重复10次（n_init）。参数 max_iter（默认300）可用于控制迭代次数：

syms = sorted(['AAPL', 'MSFT', 'CSCO', 'INTC', 'CVX', 'XOM', 'SLB', 'COP',
'JPM', 'WFC', 'USB', 'AXP', 'WMT', 'TGT', 'HD', 'COST'])
top_sp = sp500_px.loc[sp500_px.index >= '2011-01-01', syms]
kmeans = KMeans(n_clusters=5).fit(top_sp)

解释簇

Interpreting the Clusters

簇分析的一个重要部分可能涉及簇的解释。来自 kmeans 的两个最重要的输出是簇的大小和簇均值。对于前一小节中的例子，所得簇的大小由这个 R 命令给出：

km$size

1	[1] 106 186 285 288 266

在 Python 中，我们可以使用标准库中的 collections.Counter 类来获取此信息。由于实现上的差异和算法固有的随机性，结果会有所不同：

1 2	from collections import Counter Counter(kmeans.labels_)

1	Counter({4: 302, 2: 272, 0: 288, 3: 158, 1: 111})

簇的大小相对均衡。不平衡的簇可能是由遥远的异常值或与数据其余部分截然不同的记录组造成的——这两种情况都可能需要进一步检查。

您可以使用 gather 函数结合 ggplot 绘制簇的中心：

centers <- as.data.frame(t(centers))
names(centers) <- paste("Cluster", 1:5)
centers$Symbol <- row.names(centers)
centers <- gather(centers, 'Cluster', 'Mean',
-Symbol)
centers$Color = centers$Mean > 0
ggplot(centers, aes(x=Symbol, y=Mean, fill=Color)) +
geom_bar(stat='identity', position='identity', width=.75) +
facet_grid(Cluster ~
., scales='free_y')

在 Python 中创建这个可视化图的代码与我们用于 PCA 的代码类似：

centers = pd.DataFrame(kmeans.cluster_centers_, columns=syms)
f, axes = plt.subplots(5, 1, figsize=(5, 5), sharex=True)
for i, ax in enumerate(axes):
center = centers.loc[i, :]
maxPC = 1.01 * np.max(np.max(np.abs(center)))
colors = ['C0' if l > 0 else 'C1' for l in center]
ax.axhline(color='#888888')
center.plot.bar(ax=ax, color=colors)
ax.set_ylabel(f'Cluster {i + 1}')
ax.set_ylim(-maxPC, maxPC)

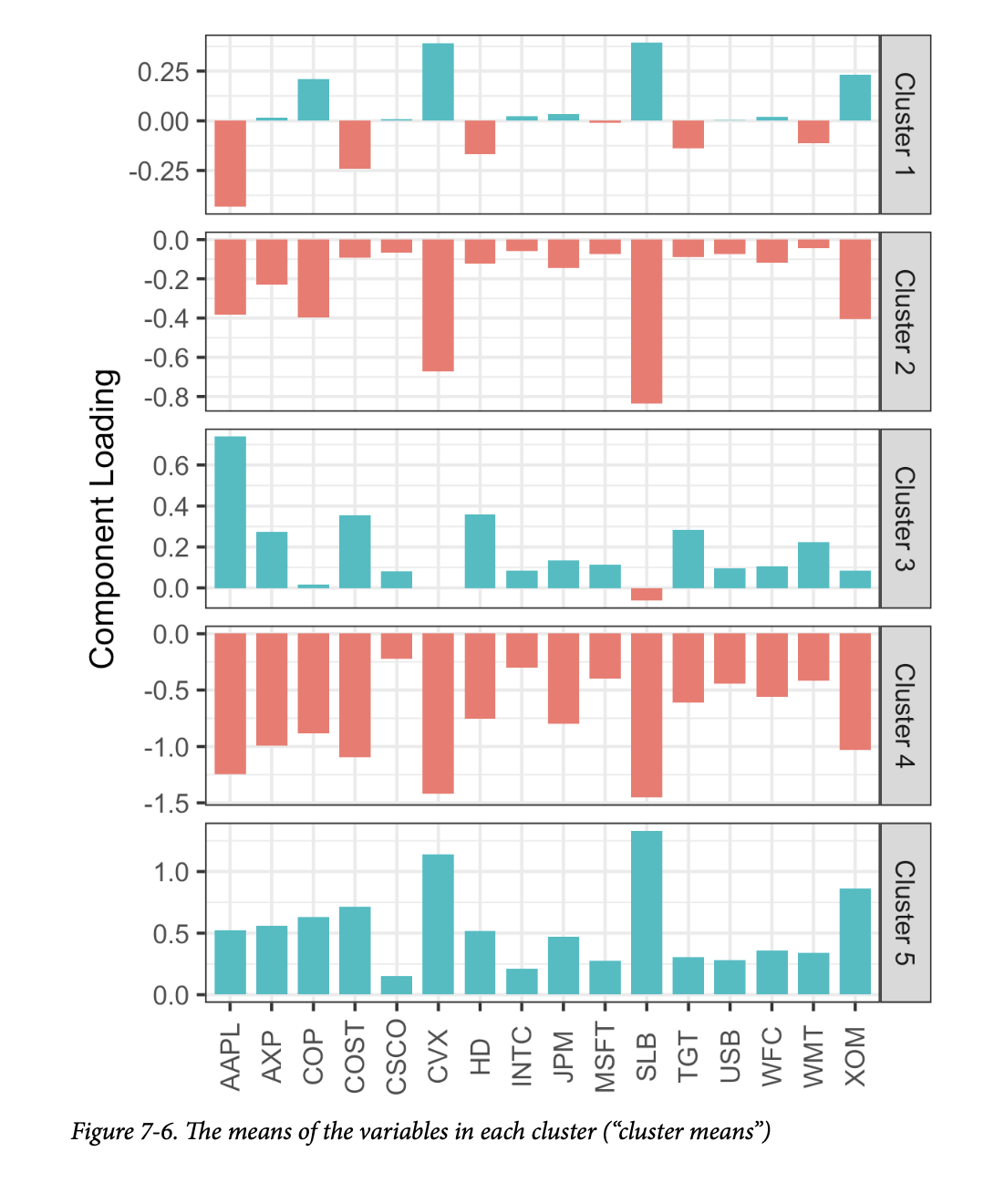
生成的图（如图7-6所示）揭示了每个簇的性质。例如，簇4和簇5分别对应于市场下行和上行的日子。簇2和簇3的特点分别是消费股市场上行和能源股市场下行的日子。最后，簇1捕捉了能源股上涨而消费股下跌的日子。

F7.6

通用注解：簇分析对比 PCA Cluster Analysis Versus PCA

簇均值的图在精神上类似于观察主成分分析 (PCA) 的载荷；参见第289页的“解释主成分”。一个主要区别是，与 PCA 不同，簇均值的符号是有意义的。PCA 识别变异的主要方向，而簇分析则寻找彼此邻近的记录组。

选择簇的数量

Selecting the Number of Clusters

K-均值算法要求您指定簇的数量 $K$。有时，簇的数量是由应用本身决定的。例如，一家管理销售团队的公司可能希望将客户聚类为不同的“人物画像”，以集中和指导销售拜访。在这种情况下，管理层面的考虑将决定所需客户细分的数量——例如，两个可能无法提供有用的客户区分，而八个可能又太多而难以管理。

在没有实际或管理考虑来决定簇数量的情况下，可以使用统计方法。目前没有一个单一的标准方法来找到“最佳”的簇数量。

一种常见的方法，称为“手肘法”（elbow method），是识别一组簇何时能解释数据中的“大部分”方差。在此集合之外添加新簇对解释方差的贡献相对较小。手肘是解释方差的累积曲线在急剧上升后趋于平缓的点，因此得名。

F7.7

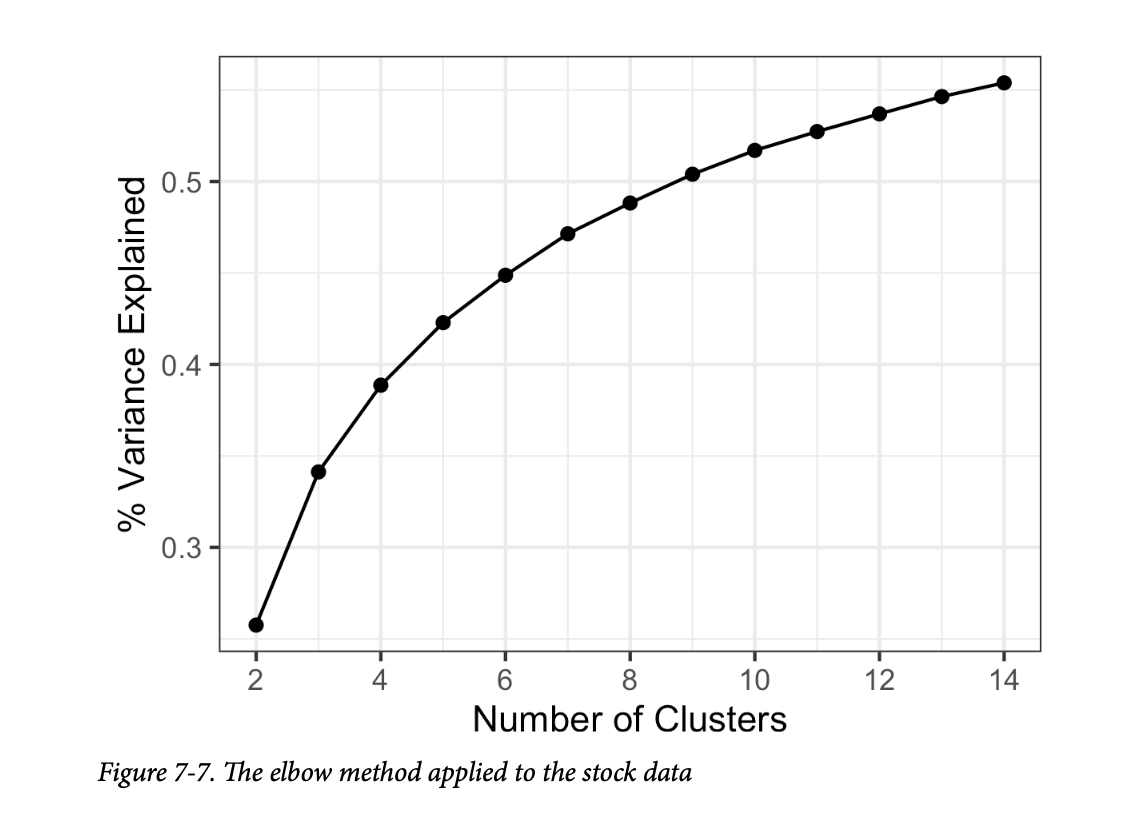
图7-7显示了贷款数据的累计方差解释百分比，簇的数量从2到15不等。在这个例子中，手肘在哪里？没有一个明显的候选点，因为解释方差的增量增加是逐渐下降的。这在没有明确界定簇的数据中是相当典型的。这也许是手肘法的一个缺点，但它确实揭示了数据的性质。

在 R 中，kmeans 函数没有提供应用手肘法的单一命令，但可以很容易地从 kmeans 的输出中应用，如下所示：

pct_var <- data.frame(pct_var = 0,
num_clusters = 2:14)
totalss <- kmeans(df, centers=14, nstart=50, iter.max=100)$totss
for (i in 2:14) {
kmCluster <- kmeans(df, centers=i, nstart=50, iter.max=100)
pct_var[i-1, 'pct_var'] <- kmCluster$betweenss / totalss
}

对于 KMeans 的结果，我们从 inertia_ 属性中获取此信息。转换为 pandas 数据框后，我们可以使用其 plot 方法来创建图表：

inertia = []
for n_clusters in range(2, 14):
kmeans = KMeans(n_clusters=n_clusters, random_state=0).fit(top_sp)
inertia.append(kmeans.inertia_ / n_clusters)
inertias = pd.DataFrame({'n_clusters': range(2, 14), 'inertia': inertia})
ax = inertias.plot(x='n_clusters', y='inertia')
plt.xlabel('Number of clusters(k)')
plt.ylabel('Average Within-Cluster Squared Distances')
plt.ylim((0, 1.1 * inertias.inertia.max()))
ax.legend().set_visible(False)

在评估要保留多少个簇时，也许最重要的检验是：这些簇在新数据上复制的可能性有多大？这些簇是否可解释，并且与数据的总体特征相关，还是仅仅反映了一个特定的实例？您可以通过使用交叉验证来部分评估这一点；参见第155页的“交叉验证”。

总的来说，没有一个单一的规则可以可靠地指导应该产生多少个簇。

通用注解：

有几种更正式的方法可以根据统计学或信息论来确定簇的数量。例如，Robert Tibshirani、Guenther Walther 和 Trevor Hastie 提出了一种基于统计理论的“间隙（gap）”统计量来识别手肘。对于大多数应用来说，理论方法可能不是必需的，甚至不一定是合适的。

关键思想

所需的簇数量 $K$ 由用户选择。
算法通过迭代地将记录分配给最近的簇均值来发展簇，直到簇分配不再改变为止。
通常，实际考虑主导 $K$ 的选择；不存在一个由统计学决定的最佳簇数量。

层次聚类

Hierarchical Clustering

层次聚类（Hierarchical clustering）是 K-均值的一种替代方案，它可以产生截然不同的簇。层次聚类允许用户可视化指定不同数量簇的效果。它在发现异常或离群的群体或记录方面更为敏感。层次聚类还适合于直观的图形显示，从而更容易解释簇。

层次聚类的关键术语

树状图（Dendrogram） 记录及其所属簇层次结构的视觉表示。
距离（Distance） 衡量一条记录与另一条记录有多近的度量。
相异度（Dissimilarity） 衡量一个簇与另一个簇有多近的度量。

层次聚类的灵活性是有代价的，它不能很好地扩展到拥有数百万条记录的大型数据集。即使对于只有数万条记录的适度大小的数据，层次聚类也可能需要密集的计算资源。事实上，层次聚类的大多数应用都集中在相对较小的数据集上。

一个简单的例子

层次聚类处理包含 $n$ 条记录和 $p$ 个变量的数据集，并基于两个基本构建块：

一个距离度量 $d_{i,j}$，用于衡量两条记录 $i$ 和 $j$ 之间的距离。
一个相异度度量 $D_{A,B}$，用于根据每个簇成员之间的距离 $d_{i,j}$ 来衡量两个簇 $A$ 和 $B$ 之间的差异。

对于涉及数值数据的应用，最重要的选择是相异度度量。层次聚类首先将每条记录设置为一个单独的簇，然后迭代地将最不相似的簇合并。

在 R 中，hclust 函数可用于执行层次聚类。hclust 与 kmeans 的一个巨大区别是，它作用于成对距离 $d_{i,j}$，而不是数据本身。您可以使用 dist 函数来计算这些距离。例如，以下代码对一组公司的股票回报应用层次聚类：

syms1 <- c('GOOGL', 'AMZN', 'AAPL', 'MSFT', 'CSCO', 'INTC', 'CVX', 'XOM', 'SLB',
'COP', 'JPM', 'WFC', 'USB', 'AXP', 'WMT', 'TGT', 'HD', 'COST')
# take transpose: to cluster companies, we need the stocks along the rows
df <- t(sp500_px[row.names(sp500_px) >= '2011-01-01', syms1])
d <- dist(df)
hcl <- hclust(d)

聚类算法将对数据框的记录（行）进行聚类。因为我们想对公司进行聚类，所以我们需要转置（t）数据框，将股票放在行中，日期放在列中。

scipy 包在 scipy.cluster.hierarchy 模块中提供了许多不同的层次聚类方法。这里我们使用 linkage 函数和“complete”（完全）方法：

syms1 = ['AAPL', 'AMZN', 'AXP', 'COP', 'COST', 'CSCO', 'CVX', 'GOOGL', 'HD',
'INTC', 'JPM', 'MSFT', 'SLB', 'TGT', 'USB', 'WFC', 'WMT', 'XOM']
df = sp500_px.loc[sp500_px.index >= '2011-01-01', syms1].transpose()
Z = linkage(df, method='complete')

树状图

The Dendrogram

层次聚类可以自然地以树的形式进行图形化展示，这被称为树状图（dendrogram）。这个名字来源于希腊词根 dendro（树）和 gramma（图画）。在 R 中，您可以使用 plot 命令轻松生成它：

plot(hcl)

在 Python 中，我们可以使用 dendrogram 方法来绘制 linkage 函数的结果：

fig, ax = plt.subplots(figsize=(5, 5))
dendrogram(Z, labels=df.index, ax=ax, color_threshold=0)
plt.xticks(rotation=90)
ax.set_ylabel('distance')

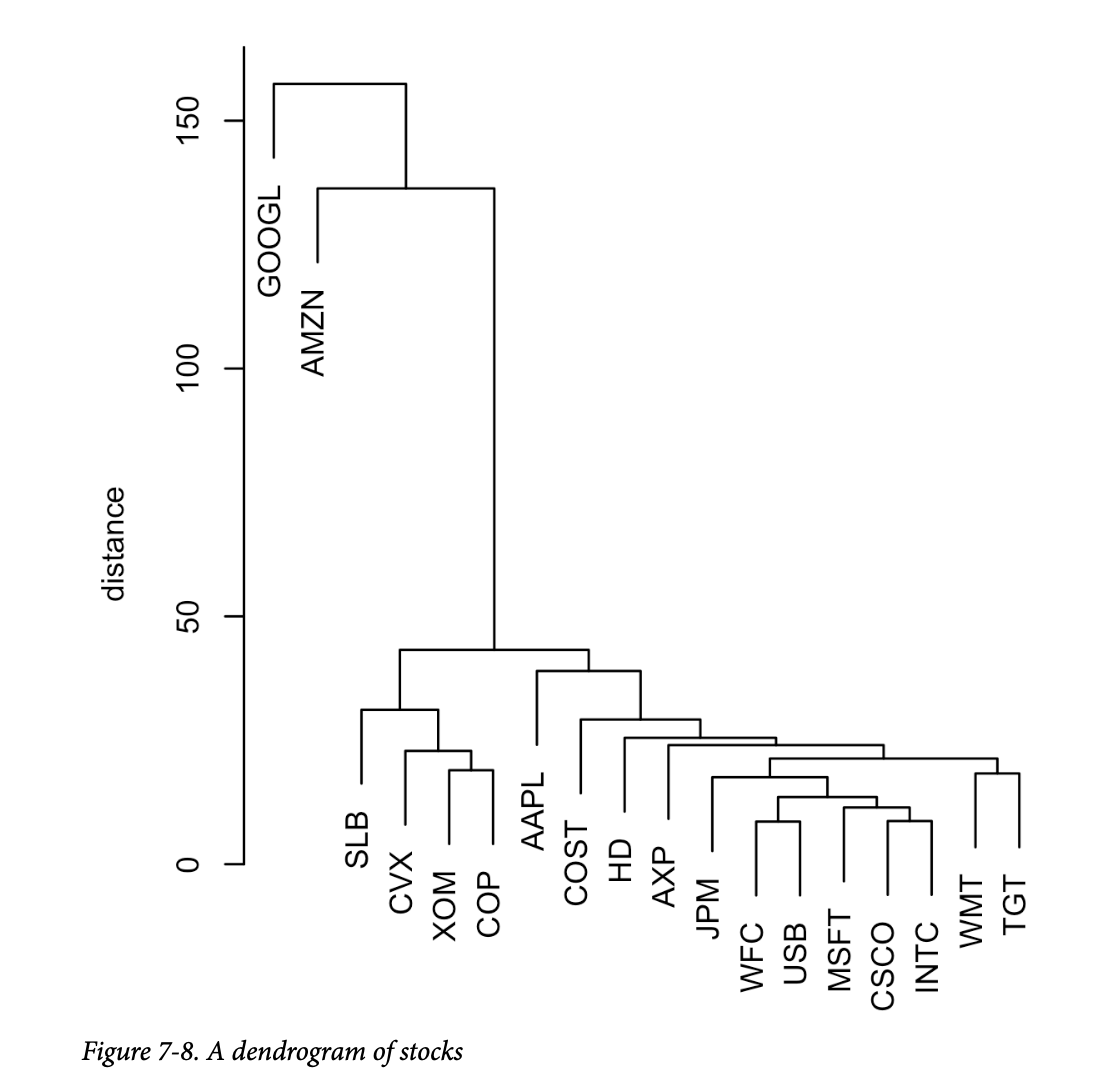
结果如图7-8所示（请注意，我们现在绘制的是相互相似的公司，而不是日期）。树的叶子对应于记录。树枝的长度表示相应簇之间的相异程度。Google 和 Amazon 的回报彼此之间以及与其他股票的回报都非常不相似。石油股（SLB, CVX, XOM, COP）在自己的簇中，苹果（AAPL）单独成簇，其余的彼此相似。

F7.8

与 K-均值不同，不必预先指定簇的数量。在图形上，您可以通过一条上下滑动的水平线来识别不同数量的簇；簇被定义为水平线与垂直线相交的地方。要提取特定数量的簇，您可以使用 cutree 函数：

1	cutree(hcl, k=4)

GOOGL AMZN AAPL MSFT CSCO INTC CVX XOM SLB COP JPM WFC 
   1    2    3    3    3    3    4    4    4    4    3    3 
 USB  AXP  WMT  TGT   HD COST 
   3    3    3    3    3    3

在 Python 中，您可以使用 fcluster 方法实现相同的功能：

memb = fcluster(Z, 4, criterion='maxclust')
memb = pd.Series(memb, index=df.index)
for key, item in memb.groupby(memb):
print(f"{key} : {', '.join(item.index)}")

提取的簇数量被设置为4，您可以看到 Google 和 Amazon 各自属于自己的簇。石油股都属于另一个簇。其余的股票都在第四个簇中。

聚类算法

The Agglomerative Algorithm

层次聚类的主要算法是聚类算法，它迭代地合并相似的簇。聚类算法从每条记录构成其自身的单个记录簇开始，然后逐步建立越来越大的簇。第一步是计算所有记录对之间的距离。

对于每对记录 $x_1, x_2, \dots, x_p$ 和 $y_1, y_2, \dots, y_p$，我们使用距离度量（参见第241页的“距离度量”）来衡量两条记录之间的距离 $d_{x,y}$。例如，我们可以使用欧几里得距离：

\[ d_{x,y} = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \dots + (x_p - y_p)^2} \] 现在我们转向簇间距离。考虑两个簇 $A$ 和 $B$，每个簇都有一组独特的记录，$A=\{a_1, a_2, \dots, a_m\}$ 和 $B=\{b_1, b_2, \dots, b_q\}$。我们可以通过使用 $A$ 的成员和 $B$ 的成员之间的距离来衡量簇之间的相异度 $D_{A,B}$。

一种相异度度量是完全链接法（complete-linkage method），它是 $A$ 和 $B$ 之间所有记录对的最大距离：

\[ D_{A,B} = \max d_{a_i, b_j} \text{ for all pairs } i, j \] 这一定义将相异度定义为所有成对差异中最大的那个。

聚类算法的主要步骤是：

创建一个初始簇集，其中每个簇由数据中的一条单一记录构成。
计算所有簇对 $C_k, C_l$ 之间的相异度 $D_{C_k, C_l}$。
合并根据 $D_{C_k, C_l}$ 测得的最不相似的两个簇 $C_k$ 和 $C_l$。
如果剩余的簇多于一个，则返回步骤2。否则，完成。

相异度度量

Measures of Dissimilarity

有四种常见的相异度度量：完全链接（complete linkage）、单链接（single linkage）、平均链接（average linkage）和最小方差（minimum variance）。这些（以及其他度量）都受到大多数层次聚类软件的支持，包括 hclust 和 linkage。

前面定义的完全链接法倾向于产生成员彼此相似的簇。
单链接法是两个簇中记录之间的最小距离： \[D_{A,B} = \min d_{a_i, b_j} \text{ for all pairs } i, j\] 这是一种“贪婪”方法，产生的簇可能包含相当不一致的元素。
平均链接法是所有距离对的平均值，代表了单链接和完全链接方法之间的一种折中。
最后，最小方差法，也称为沃德法（Ward's method），类似于 K-均值，因为它最小化簇内平方和（参见第294页的“K-均值聚类”）。

图7-9对埃克森美孚和雪佛龙的股票回报应用了使用这四种度量的层次聚类。对于每种度量，都保留了四个簇。

F7.9

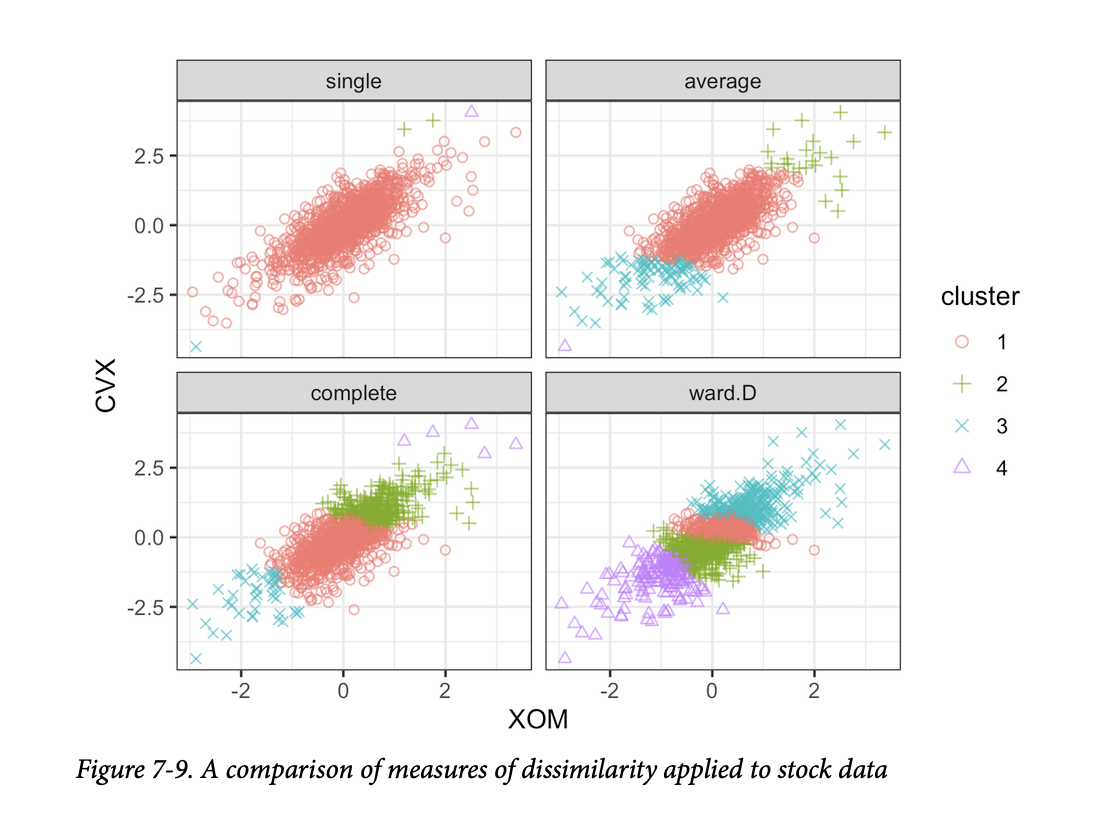
结果截然不同：单链接度量将几乎所有的点都分配给一个单独的簇。除了最小方差法（R：Ward.D；Python：ward）之外，所有度量最终都至少有一个簇只包含几个离群点。最小方差法与 K-均值聚类最相似；请与图7-5进行比较。

关键思想

层次聚类从每条记录都在其自己的簇中开始。
簇逐步与邻近的簇合并，直到所有记录都属于一个单一的簇（聚类算法）。
聚类历史被保留并绘制出来，用户可以在不预先指定簇数量的情况下，在不同阶段可视化簇的数量和结构。
簇间距离以不同的方式计算，所有这些方式都依赖于所有记录间距离的集合。

基于模型的聚类

Model-Based Clustering

像层次聚类和 K-均值这样的聚类方法是基于启发式的，主要依赖于寻找其成员彼此接近的簇，这是通过直接用数据来衡量的（不涉及概率模型）。在过去的20年里，人们投入了大量精力来开发基于模型的聚类方法。华盛顿大学的 Adrian Raftery 和其他研究人员对基于模型的聚类做出了重要贡献，包括理论和软件。这些技术以统计理论为基础，并提供了更严谨的方法来确定簇的性质和数量。例如，它们可以用于以下情况：可能有一组记录彼此相似但不一定彼此接近（例如，回报方差高的科技股），而另一组记录既相似又接近（例如，方差低的公用事业股）。

多元正态分布

Multivariate Normal Distribution

最广泛使用的基于模型的聚类方法都依赖于多元正态分布。多元正态分布是正态分布向一组 $p$ 个变量 $X_1, X_2, \dots, X_p$ 的推广。该分布由一组均值 $\mu = (\mu_1, \mu_2, \dots, \mu_p)$ 和一个协方差矩阵 $\Sigma$ 定义。协方差矩阵是衡量变量之间如何关联的度量（有关协方差的详细信息，请参见第202页的“协方差矩阵”）。协方差矩阵 $\Sigma$ 由 $p$ 个方差 $\sigma_1^2, \sigma_2^2, \dots, \sigma_p^2$ 和所有变量对 $i \neq j$ 的协方差 $\sigma_{i,j}$ 组成。将变量放在行和列中，矩阵如下所示：

\[ \Sigma = \begin{pmatrix} \sigma_1^2 & \sigma_{1,2} & \cdots & \sigma_{1,p} \\ \sigma_{2,1} & \sigma_2^2 & \cdots & \sigma_{2,p} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{p,1} & \sigma_{p,2} & \cdots & \sigma_p^2 \end{pmatrix} \]

请注意，协方差矩阵关于从左上到右下的对角线是对称的。由于 $\sigma_{i,j} = \sigma_{j,i}$，所以只有 $p(p-1)/2$ 个协方差项。总的来说，协方差矩阵有 $p(p-1)/2 + p$ 个参数。该分布表示为：

\[ (X_1, X_2, \dots, X_p) \sim N_p(\mu, \Sigma) \]

这是一种符号表示，意思是所有变量都呈正态分布，并且整体分布由变量均值向量和协方差矩阵完全描述。

F7.10

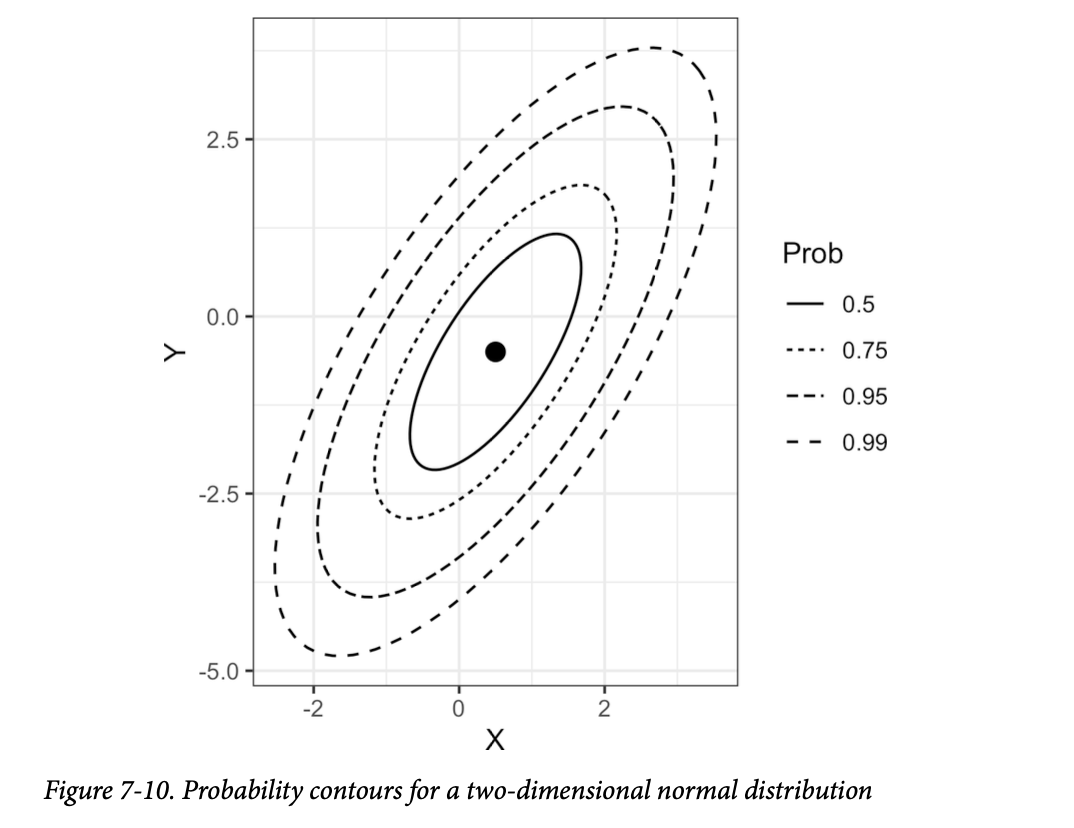
图7-10显示了两个变量 $X$ 和 $Y$ 的多元正态分布的概率等高线（例如，0.5概率等高线包含50%的分布）。

个人注：概率等高线（probability contours) 这些等高线连接着具有相同概率密度的点，就像地形图上的等高线连接着具有相同海拔的点一样。

均值为 $\mu_x = 0.5$ 和 $\mu_y = -0.5$，协方差矩阵为：

\[ \Sigma = \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix} \]

由于协方差 $\sigma_{xy}$ 是正的，因此 $X$ 和 $Y$ 正相关。

正态分布混合

Mixtures of Normals

基于模型的聚类背后的关键思想是，每条记录被假定为服从 $K$ 个多元正态分布中的一个，其中 $K$ 是簇的数量。每个分布都有不同的均值 $\mu$ 和协方差矩阵 $\Sigma$。例如，如果您有两个变量 $X$ 和 $Y$，那么每行 $(X_i, Y_i)$ 被建模为从 $K$ 个多元正态分布中的一个进行采样：$N(\mu_1, \Sigma_1), N(\mu_2, \Sigma_2), \dots, N(\mu_K, \Sigma_K)$。

R 有一个非常丰富的基于模型聚类的包，名为 mclust，最初由 Chris Fraley 和 Adrian Raftery 开发。使用这个包，我们可以对之前用 K-均值和层次聚类分析过的股票回报数据应用基于模型的聚类：

> library(mclust)
> df <- sp500_px[row.names(sp500_px) >= '2011-01-01', c('XOM', 'CVX')]
> mcl <- Mclust(df)
> summary(mcl)

Mclust VEE (ellipsoidal, equal shape and orientation) model with 2 components:
log.likelihood n df BIC ICL
-2255.134 1131 9 -4573.546 -5076.856
Clustering table:
1 2
963 168

scikit-learn 有 sklearn.mixture.GaussianMixture 类用于基于模型的聚类：

1
2
3

df = sp500_px.loc[sp500_px.index >= '2011-01-01', ['XOM', 'CVX']]
mclust = GaussianMixture(n_components=2).fit(df)
mclust.bic(df)

如果您执行此代码，会注意到计算时间比其他过程长得多。使用 predict 函数提取簇分配，我们可以对簇进行可视化：

1
2
3

cluster <- factor(predict(mcl)$classification)
ggplot(data=df, aes(x=XOM, y=CVX, color=cluster, shape=cluster)) +
geom_point(alpha=.8)

以下是创建类似图形的 Python 代码：

fig, ax = plt.subplots(figsize=(4, 4))
colors = [f'C{c}' for c in mclust.predict(df)]
df.plot.scatter(x='XOM', y='CVX', c=colors, alpha=0.5, ax=ax)
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)

结果如图7-11所示。存在两个簇：一个簇在数据的中间，另一个簇在数据的外缘。这与使用 K-均值（图7-5）和层次聚类（图7-9）获得的簇非常不同，后者找到的是紧凑的簇。

F7.11

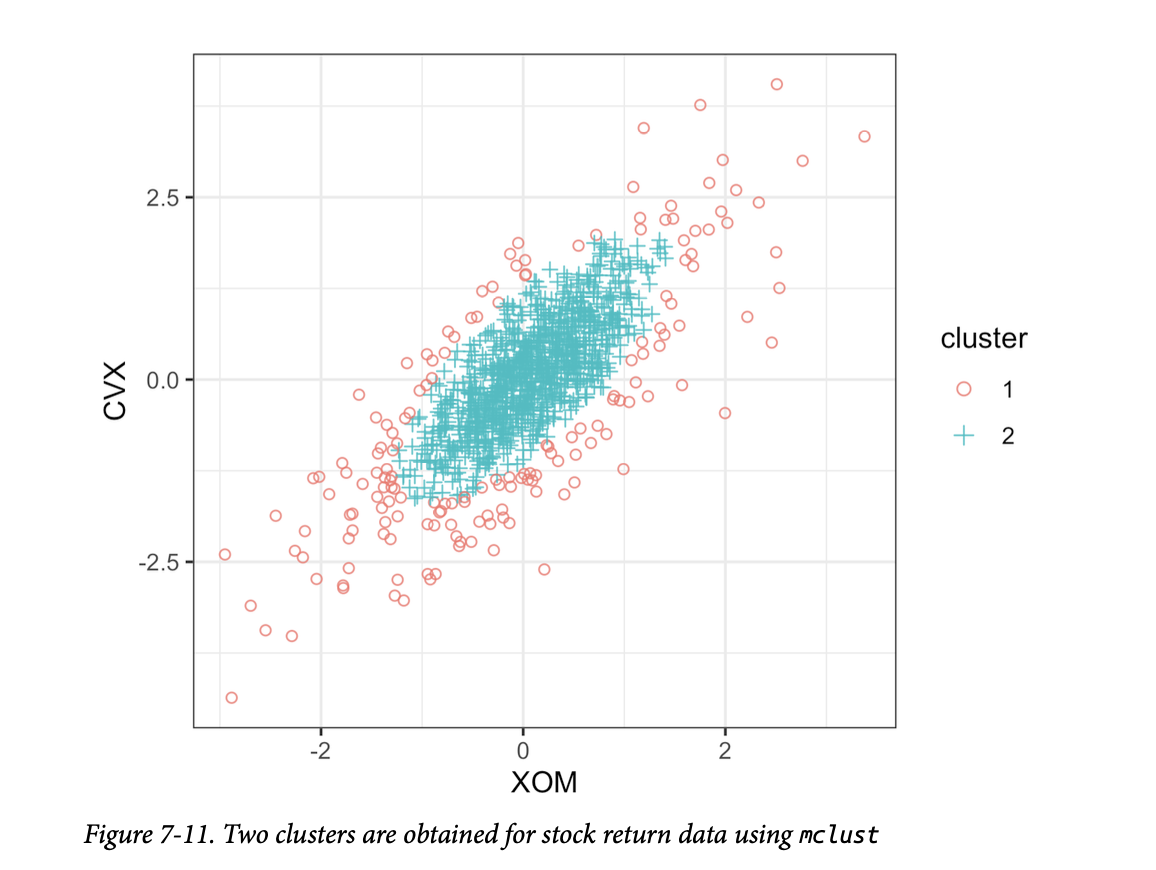
您可以使用 summary 函数提取正态分布的参数：

1	> summary(mcl, parameters=TRUE)$mean

1
2
3

          [,1]       [,2]
XOM 0.05783847 -0.04374944
CVX 0.07363239 -0.21175715

1	> summary(mcl, parameters=TRUE)$variance

, , 1

          XOM       CVX
XOM 0.3002049 0.3060989
CVX 0.3060989 0.5496727

, , 2

         XOM      CVX
XOM 1.046318 1.066860
CVX 1.066860 1.915799

在 Python 中，您可以从结果的 means_ 和 covariances_ 属性中获取此信息：

print('Mean')
print(mclust.means_)
print('Covariances')
print(mclust.covariances_)

这两个分布有相似的均值和相关性，但第二个分布有大得多的方差和协方差。由于算法的随机性，不同运行的结果可能会略有差异。

mclust 产生的簇可能看起来令人惊讶，但事实上，它们说明了该方法的统计性质。基于模型的聚类的目标是找到最能拟合的多元正态分布集。股票数据似乎具有类似正态的形状：参见图7-10的等高线。然而，实际上，股票回报的分布比正态分布具有更长的尾部。为了解决这个问题，mclust 将一个分布拟合到大部分数据上，然后拟合第二个具有更大方差的分布。

选择簇的数量

Selecting the Number of Clusters

与 K-均值和层次聚类不同，mclust 在 R 中自动选择簇的数量（在本例中为两个）。它通过选择贝叶斯信息准则（BIC）具有最大值的簇数量来实现（BIC类似于AIC；参见第156页的“模型选择和逐步回归”）。BIC 通过选择拟合最佳的模型来工作，同时对模型中的参数数量进行惩罚。在基于模型的聚类中，添加更多的簇总是会改善拟合，但代价是引入额外的模型参数。

警告：

请注意，在大多数情况下，BIC通常是最小化的。mclust 包的作者决定定义 BIC 为相反的符号，以便更容易解释绘图。

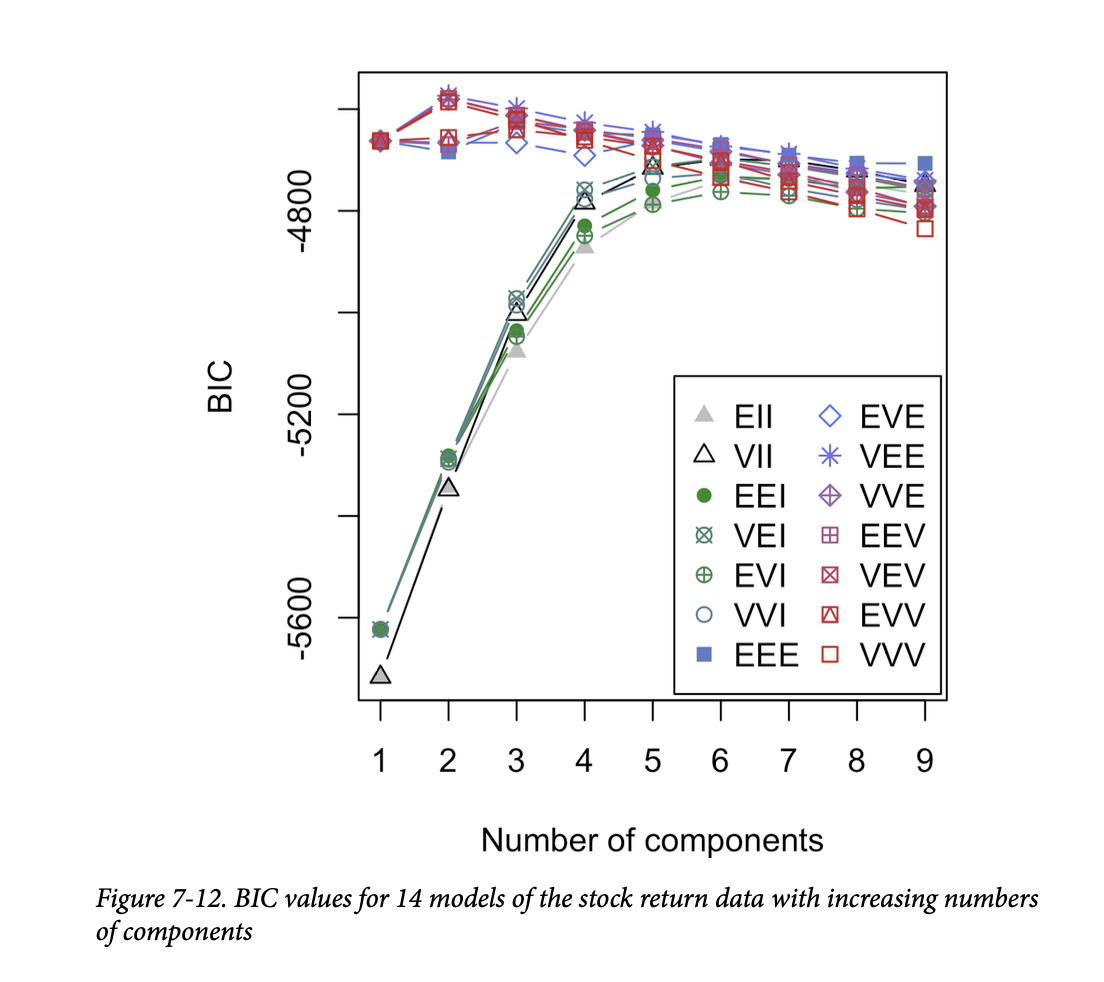
mclust 拟合14个不同模型，并随着组件数量的增加而自动选择最佳模型。您可以使用 mclust 中的函数绘制这些模型的 BIC 值：

1	plot(mcl, what='BIC', ask=FALSE)

簇的数量（或者说不同多元正态模型（组件）的数量）显示在 x 轴上（参见图7-12）。

F7.12

另一方面，GaussianMixture 的实现不会尝试各种组合。如下所示，使用 Python 运行多种组合是直截了当的。这个实现按惯例定义 BIC，因此计算出的 BIC 值为正，我们需要将其最小化。

results = []
covariance_types = ['full', 'tied', 'diag', 'spherical']
for n_components in range(1, 9):
    for covariance_type in covariance_types:
        mclust = GaussianMixture(n_components=n_components, warm_start=True,
                                 covariance_type=covariance_type)
        mclust.fit(df)
        results.append({
            'bic': mclust.bic(df),
            'n_components': n_components,
            'covariance_type': covariance_type,
        })

results = pd.DataFrame(results)
colors = ['C0', 'C1', 'C2', 'C3']
styles = ['C0-','C1:','C0-.', 'C1--']
fig, ax = plt.subplots(figsize=(4, 4))
for i, covariance_type in enumerate(covariance_types):
    subset = results.loc[results.covariance_type == covariance_type, :]
    subset.plot(x='n_components', y='bic', ax=ax, label=covariance_type,
                kind='line', style=styles[i])

使用 warm_start 参数，计算将重用上一次拟合的信息。这将加快后续计算的收敛速度。

这个图与用于确定 K-均值簇数量的手肘图相似，不同之处在于绘制的值是BIC而不是解释方差的百分比（参见图7-7）。一个很大的区别是，mclust 没有显示一条线，而是显示14条不同的线！这是因为 mclust 实际上为每种簇大小拟合了14个不同的模型，并最终选择了最拟合的模型。GaussianMixture 实现的方法较少，因此线条数量只有四条。

为什么 mclust 要拟合这么多模型来确定最佳多元正态集呢？这是因为有不同的方法来参数化协方差矩阵 $\Sigma$ 以进行模型拟合。在大多数情况下，您不需要担心模型的细节，只需使用 mclust 选择的模型即可。在本例中，根据 BIC，三个不同的模型（称为 VEE、VEV 和 VVE）使用两个组件提供了最佳拟合。

通用注解：

基于模型的聚类是一个丰富且快速发展的研究领域，本书的涵盖范围只占该领域的一小部分。事实上，mclust 的帮助文件目前长达154页。对于数据科学家遇到的大多数问题来说，深入研究基于模型的聚类的细微差别可能超出了需要。

基于模型的聚类技术确实存在一些局限性。这些方法需要一个潜在的数据模型假设，而聚类结果非常依赖于这个假设。其计算要求甚至高于层次聚类，这使得它难以扩展到大数据。最后，该算法比其他方法更复杂，更难理解。

关键思想

假设簇源自不同的数据生成过程，具有不同的概率分布。
拟合不同的模型，假设有不同数量的（通常为正态）分布。
该方法选择拟合数据良好且不使用过多参数（即，不过拟合）的模型（以及相关的簇数量）。

缩放和分类变量

Scaling and Categorical Variables

无监督学习技术通常要求数据经过适当的缩放。这与许多回归和分类技术不同，在这些技术中缩放并不重要（一个例外是 K-近邻；参见第238页的“K-近邻”）。

数据缩放的关键术语

缩放（Scaling） 压缩或扩展数据，通常是为了将多个变量带到相同的尺度。
归一化（Normalization） 一种缩放方法——减去均值并除以标准差。同义词：标准化（Standardization）
Gower's distance 一种应用于混合数值和分类数据的缩放算法，将所有变量带到0-1的范围。

例如，对于个人贷款数据，变量具有截然不同的单位和量级。有些变量的值相对较小（例如，工作年限），而另一些变量的值则非常大（例如，以美元计的贷款金额）。如果数据没有经过缩放，那么 PCA、K-均值和其他聚类方法将被大值的变量主导，而忽略小值的变量。

对于某些聚类过程，分类数据可能会带来特殊问题。与 K-近邻一样，无序因子变量通常使用独热编码（one hot encoding）转换为一组二元（0/1）变量（参见第242页的“独热编码”）。二元变量不仅可能与其他数据处于不同的尺度，而且二元变量只有两个值这一事实，对于 PCA 和 K-均值等技术来说也可能存在问题。

变量缩放

Scaling the Variables

在应用聚类过程之前，需要对具有截然不同尺度和单位的变量进行适当的归一化。例如，让我们在不进行归一化的情况下，将 kmeans 应用于一组贷款违约数据：

defaults <- loan_data[loan_data$outcome=='default',]
df <- defaults[, c('loan_amnt', 'annual_inc', 'revol_bal', 'open_acc',
'dti', 'revol_util')]
km <- kmeans(df, centers=4, nstart=10)
centers <- data.frame(size=km$size, km$centers)
round(centers, digits=2)

   size loan_amnt annual_inc revol_bal open_acc  dti revol_util
1    52  22570.19  489783.40  85161.35    13.33 6.91      59.65
2  1192  21856.38  165473.54  38935.88    12.61 13.48      63.67
3 13902  10606.48   42500.30  10280.52     9.59 17.71      58.11
4  7525  18282.25   83458.11  19653.82    11.66 16.77      62.27

以下是相应的 Python 代码：

defaults = loan_data.loc[loan_data['outcome'] == 'default',]
columns = ['loan_amnt', 'annual_inc', 'revol_bal', 'open_acc',
'dti', 'revol_util']
df = defaults[columns]
kmeans = KMeans(n_clusters=4, random_state=1).fit(df)
counts = Counter(kmeans.labels_)
centers = pd.DataFrame(kmeans.cluster_centers_, columns=columns)
centers['size'] = [counts[i] for i in range(4)]
centers

变量 annual_inc 和 revol_bal 主导了簇，并且簇的大小差异很大。簇1只有52个成员，其收入和循环信贷余额相对较高。

一种常见的变量缩放方法是将它们转换为z-分数，即减去均值并除以标准差。这被称为标准化或归一化（关于使用 z-分数的更多讨论，请参见第243页的“标准化（归一化，z-分数）”）：

\[ z = \frac{x-\bar{x}}{s} \]

让我们看看将 kmeans 应用于归一化数据后簇发生了什么：

df0 <- scale(df)
km0 <- kmeans(df0, centers=4, nstart=10)
centers0 <- scale(km0$centers, center=FALSE,
scale=1 / attr(df0, 'scaled:scale'))
centers0 <- scale(centers0, center=-attr(df0, 'scaled:center'), scale=FALSE)
centers0 <- data.frame(size=km0$size, centers0)
round(centers0, digits=2)

   size loan_amnt annual_inc revol_bal open_acc  dti revol_util
1  7355  10467.65   51134.87  11523.31     7.48 15.78      77.73
2  5309  10363.43   53523.09   6038.26     8.68 11.32      30.70
3  3713  25894.07  116185.91  32797.67    12.41 16.22      66.14
4  6294  13361.61   55596.65  16375.27    14.25 24.23      59.61

在 Python 中，我们可以使用 scikit-learn 的 StandardScaler。inverse_transform 方法允许将簇中心转换回原始尺度：

scaler = preprocessing.StandardScaler()
df0 = scaler.fit_transform(df * 1.0)
kmeans = KMeans(n_clusters=4, random_state=1).fit(df0)
counts = Counter(kmeans.labels_)
centers = pd.DataFrame(scaler.inverse_transform(kmeans.cluster_centers_),
columns=columns)
centers['size'] = [counts[i] for i in range(4)]
centers

簇的大小更加均衡，并且簇不再被 annual_inc 和 revol_bal 主导，从而揭示了数据中更有趣的结构。请注意，在上述代码中，中心被重新缩放回原始单位。如果我们没有对它们进行缩放，得到的值将是 z-分数，因此可解释性会降低。

通用注解：

缩放对于 PCA 也非常重要。使用 z-分数等同于在计算主成分时使用相关矩阵（参见第30页的“相关性”），而不是协方差矩阵。计算 PCA 的软件通常都有一个使用相关矩阵的选项（在 R 中，princomp 函数有一个 cor 参数）。

主导变量

Dominant Variables

即使变量以相同的尺度测量并准确反映相对重要性（例如，对股票价格的走势），有时重新缩放变量仍然是有用的。

假设我们在第289页的“解释主成分”中添加了 Google (GOOGL) 和 Amazon (AMZN) 到分析中。下面我们来看看如何在 R 中完成：

syms <- c('GOOGL', 'AMZN', 'AAPL', 'MSFT', 'CSCO', 'INTC', 'CVX', 'XOM',
'SLB', 'COP', 'JPM', 'WFC', 'USB', 'AXP', 'WMT', 'TGT', 'HD', 'COST')
top_sp1 <- sp500_px[row.names(sp500_px) >= '2005-01-01', syms]
sp_pca1 <- princomp(top_sp1)
screeplot(sp_pca1)

在 Python 中，我们按如下方式获取碎石图：

syms = ['GOOGL', 'AMZN', 'AAPL', 'MSFT', 'CSCO', 'INTC', 'CVX', 'XOM',
'SLB', 'COP', 'JPM', 'WFC', 'USB', 'AXP', 'WMT', 'TGT', 'HD', 'COST']
top_sp1 = sp500_px.loc[sp500_px.index >= '2005-01-01', syms]
sp_pca1 = PCA()
sp_pca1.fit(top_sp1)
explained_variance = pd.DataFrame(sp_pca1.explained_variance_)
ax = explained_variance.head(10).plot.bar(legend=False, figsize=(4, 4))
ax.set_xlabel('Component')

F7.13

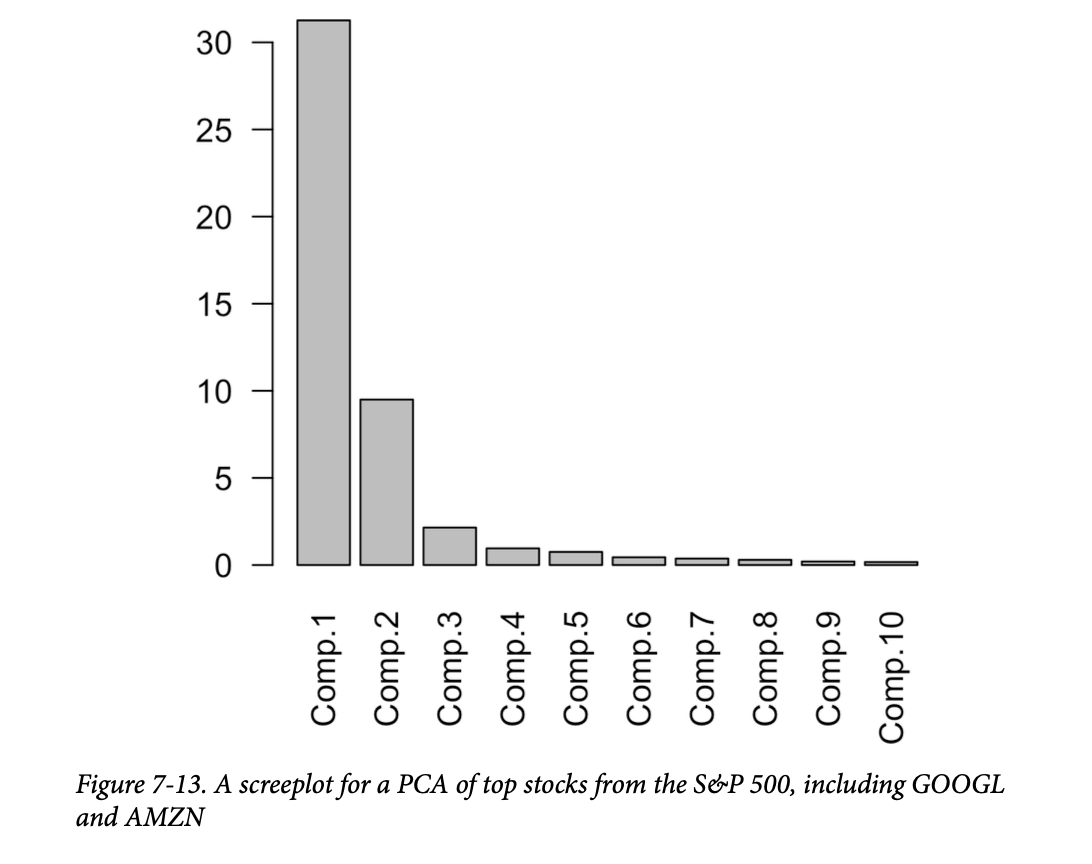
碎石图显示了前几个主成分的方差。在本例中，图7-13中的碎石图显示第一和第二成分的方差比其他成分大得多。这通常表明一个或两个变量主导了载荷。在这个例子中，情况确实如此：

1	round(sp_pca1$loadings[,1:2], 3)

       Comp.1 Comp.2
GOOGL   0.781  0.609
AMZN    0.593 -0.792
AAPL    0.078  0.004
MSFT    0.029  0.002
CSCO    0.017 -0.001
INTC    0.020 -0.001
CVX     0.068 -0.021
XOM     0.053 -0.005
...

在 Python 中，我们使用以下代码：

1 2	loadings = pd.DataFrame(sp_pca1.components_[0:2, :], columns=top_sp1.columns) loadings.transpose()

前两个主成分几乎完全由 GOOGL 和 AMZN 主导。这是因为 GOOGL 和 AMZN 的股价波动主导了变异性。

为了处理这种情况，您可以保持现状、重新缩放变量（参见第319页的“变量缩放”），或者将主导变量从分析中排除并单独处理。没有“正确”的方法，处理方式取决于具体的应用。

分类数据和 Gower's 距离

Categorical Data and Gower’s Distance

对于分类数据，您必须将其转换为数值数据，可以通过排序（对于有序因子）或编码为一组二元（虚拟）变量来完成。如果数据由混合的连续和二元变量组成，您通常会希望缩放变量，使其范围相似；参见第319页的“变量缩放”。一种流行的方法是使用 Gower's 距离。

Gower's 距离的基本思想是根据数据的类型对每个变量应用不同的距离度量：

对于数值变量和有序因子，距离被计算为两条记录之间差值的绝对值（曼哈顿距离）。
对于分类变量，如果两条记录的类别不同，距离为1；如果类别相同，距离为0。

Gower's 距离的计算过程如下：

计算每条记录所有变量对 $i$ 和 $j$ 的距离 $d_{i,j}$。
将每对距离 $d_{i,j}$ 进行缩放，使其最小值为0，最大值为1。
使用简单或加权平均值，将变量之间的成对缩放距离相加，以创建距离矩阵。

为了说明 Gower's 距离，我们从 R 中的贷款数据中提取几行：

> x <- loan_data[1:5, c('dti', 'payment_inc_ratio', 'home_', 'purpose_')]
> x
# A tibble: 5 × 4
    dti payment_inc_ratio home_     purpose_
  <dbl>             <dbl> <fct>     <fct>
1  1.00             2.97  OWN       credit_card
2  5.55             3.83  RENT      debt_consolidation
3 18.08             7.69  MORTGAGE  debt_consolidation
4 10.08             5.58  RENT      home_improvement
5  6.56             2.92  MORTGAGE  major_purchase

R 的 cluster 包中的 daisy 函数可用于计算 Gower's 距离：

1 2	library(cluster) daisy(x, metric='gower')

Dissimilarities :
          1         2         3         4
2 0.6220479                              
3 0.6863877 0.8143398                    
4 0.6329040 0.7608561 0.4307083          
5 0.3772789 0.5389727 0.3091088 0.5056250

Metric :  mixed ; Types = I, I, N, N 
Number of objects : 5

截至撰写本文时，Gower's 距离在任何流行的 Python 包中都不可用。然而，正在进行将其包含在 scikit-learn 中的活动。一旦实现发布，我们将更新随附的源代码。

所有距离都在0到1之间。距离最大的记录对是2和3：它们的 home 和 purpose 值都不同，并且 dti（债务收入比）和 payment_inc_ratio 的水平也大相径庭。记录3和5的距离最小，因为它们的 home 和 purpose 值相同。

您可以将从 daisy 计算出的 Gower's 距离矩阵传递给 hclust 进行层次聚类（参见第304页的“层次聚类”）：

df <- defaults[sample(nrow(defaults), 250),
c('dti', 'payment_inc_ratio', 'home', 'purpose')]
d = daisy(df, metric='gower')
hcl <- hclust(d)
dnd <- as.dendrogram(hcl)
plot(dnd, leaflab='none')

F7.14

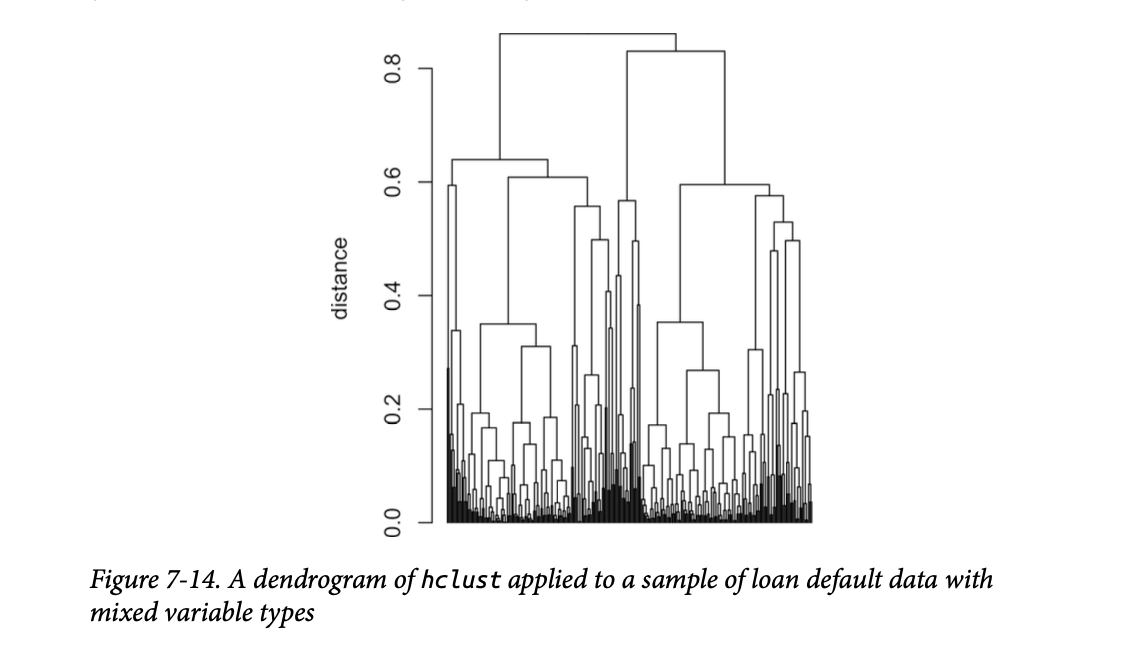
生成的树状图如图7-14所示。单个记录在 x 轴上无法区分，但我们可以将树状图在0.5处水平切割，并使用此代码检查其中一个子树中的记录：

1 2	dnd_cut <- cut(dnd, h=0.5) df[labels(dnd_cut$lower[[1]]),]

      dti payment_inc_ratio home_          purpose_
44532 21.22          8.37694   OWN debt_consolidation
39826 22.59          6.22827   OWN debt_consolidation
13282 31.00          9.64200   OWN debt_consolidation
31510 26.21         11.94380   OWN debt_consolidation
6693  26.96          9.45600   OWN debt_consolidation
7356  25.81          9.39257   OWN debt_consolidation
9278  21.00         14.71850   OWN debt_consolidation
13520 29.00         18.86670   OWN debt_consolidation
14668 25.75         17.53440   OWN debt_consolidation
19975 22.70         17.12170   OWN debt_consolidation
23492 22.68         18.50250   OWN debt_consolidation

这个子树完全由拥有房产且贷款目的标记为“债务合并”的记录组成。虽然并非所有子树都存在严格的分离，但这表明分类变量倾向于在簇中被分组在一起。

混合数据的聚类问题

Problems with Clustering Mixed Data

K-均值和 PCA 最适合连续变量。对于较小的数据集，最好使用带有 Gower's 距离的层次聚类。原则上，K-均值也可以应用于二元或分类数据。通常会使用“独热编码”表示法（参见第242页的“独热编码”）将分类数据转换为数值。然而，在实践中，将 K-均值和 PCA 与二元数据一起使用可能会很困难。

如果使用标准的 z-分数，二元变量将主导簇的定义。这是因为 0/1 变量只取两个值，而 K-均值可以通过将所有值为0或1的记录分配给单个簇来获得较小的簇内平方和。例如，将 kmeans 应用于包含因子变量 home 和 pub_rec_zero 的贷款违约数据，如R中所示：

df <- model.matrix(~ -1 + dti + payment_inc_ratio + home_ + pub_rec_zero,
data=defaults)
df0 <- scale(df)
km0 <- kmeans(df0, centers=4, nstart=10)
centers0 <- scale(km0$centers, center=FALSE,
scale=1/attr(df0, 'scaled:scale'))
round(scale(centers0, center=-attr(df0, 'scaled:center'), scale=FALSE), 2)

   dti payment_inc_ratio home_MORTGAGE home_OWN home_RENT pub_rec_zero
1 17.20              9.27          0.00     1.00      0.00         0.92
2 16.99              9.11          0.00     0.00      1.00         1.00
3 16.50              8.06          0.52     0.00      0.48         1.00
4 17.46              8.42          1.00     0.00      0.00         0.00

在 Python 中：

columns = ['dti', 'payment_inc_ratio', 'home_', 'pub_rec_zero']
df = pd.get_dummies(defaults[columns])
scaler = preprocessing.StandardScaler()
df0 = scaler.fit_transform(df * 1.0)
kmeans = KMeans(n_clusters=4, random_state=1).fit(df0)
centers = pd.DataFrame(scaler.inverse_transform(kmeans.cluster_centers_),
columns=df.columns)
centers

前四个簇本质上是因子变量不同水平的代理。为了避免这种行为，您可以将二元变量缩放，使其方差小于其他变量。另外，对于非常大的数据集，您可以将聚类应用于具有特定分类值的不同数据子集。例如，您可以将聚类分别应用于那些有房贷的人、拥有房产的人或租房的人所获得的贷款。

关键思想

以不同尺度测量的变量需要转换为相似的尺度，以确保它们对算法的影响不主要由其尺度决定。
一种常见的缩放方法是归一化（标准化）——减去均值并除以标准差。
另一种方法是 Gower's 距离，它将所有变量缩放到0-1的范围（常用于混合数值和分类数据）。

总结

对于数值数据的降维，主要工具是主成分分析或 K-均值聚类。两者都需要注意数据的正确缩放，以确保有意义的数据缩减。

对于高度结构化且簇分隔良好的数据进行聚类时，所有方法可能都会产生相似的结果。每种方法都有其自身的优势。K-均值可以扩展到非常大的数据，且易于理解。层次聚类可以应用于混合数据类型——数值和分类——并易于进行直观的显示（树状图）。基于模型的聚类建立在统计理论基础上，提供了一种比启发式方法更严谨的方法。然而，对于非常大的数据，K-均值是主要使用的方法。

对于像贷款和股票数据这样的嘈杂数据（以及数据科学家将面临的大部分数据），选择就更加严峻了。K-均值、层次聚类，尤其是基于模型的聚类，都会产生截然不同的解决方案。数据科学家应该如何进行？不幸的是，没有简单的经验法则来指导选择。最终，使用的方法将取决于数据大小和应用的目标。

第7章 无监督学习

主成分分析

一个简单的例子

计算主成分

解释主成分

对应分析

K-均值聚类

一个简单的例子

K-均值算法

解释簇

选择簇的数量

层次聚类

一个简单的例子

树状图

聚类算法

相异度度量

基于模型的聚类

多元正态分布

正态分布混合

选择簇的数量

缩放和分类变量

变量缩放

主导变量

分类数据和 Gower's 距离

混合数据的聚类问题

总结

第7章无监督学习