第6章 统计机器学习

发表于 分类于

《Practical Statistics for Data Scientists》书籍英文版
《面向数据科学家的实用统计学》中文版书籍

第6章 统计机器学习

Statistical Machine Learning

统计学在近期发展中，致力于开发更强大、更自动化的预测建模技术，涵盖了回归和分类。这些方法与上一章讨论的方法一样，都是有监督学习——它们通过在已知结果的数据上进行训练，来学习如何预测新数据的结果。它们属于统计机器学习的范畴，与经典统计方法不同之处在于，它们是数据驱动的，并且不试图对数据强加线性的或其他整体结构。例如，K-最近邻(K-Nearest Neighbors)方法非常简单：根据相似记录的分类方式来对一条记录进行分类。最成功和应用最广泛的技术是基于集成学习(ensemble learning)并应用于决策树(decision trees.)的方法。集成学习的基本思想是使用多个模型来形成预测，而不是仅仅使用一个单一模型。决策树是一种灵活且自动化的技术，用于学习预测变量和结果变量之间关系的规则。事实证明，将集成学习与决策树相结合，可以产生一些性能最佳的现成预测建模技术。

许多统计机器学习技术的发展，可以追溯到加州大学伯克利分校的统计学家 Leo Breiman（参见图6-1）和斯坦福大学的 Jerry Friedman。 他们的工作，以及伯克利和斯坦福其他研究人员的工作，始于1984年对树模型的开发。随后在20世纪90年代开发的装袋法（bagging）和提升法（boosting）等集成方法，奠定了统计机器学习的基础。

F6.1

通用注解：

机器学习与统计学（Machine Learning Versus Statistics）

在预测建模的背景下，机器学习和统计学有什么区别？这两个学科之间没有明确的界限。机器学习更倾向于开发高效算法，以处理大规模数据来优化预测模型。而统计学通常更关注概率理论和模型的底层结构。装袋法和随机森林（参见第259页的“装袋法与随机森林”）稳固地属于统计学阵营。另一方面，提升法（参见第270页的“提升法”）在这两个学科中都有发展，但在机器学习方面获得了更多关注。不管历史如何，提升法所展现的潜力确保了它将在统计学和机器学习中都蓬勃发展。

K-最近邻

K-Nearest Neighbors

K-最近邻（KNN）背后的思想非常简单。对于每一条待分类或预测的记录：

  1. 找到K个特征相似（即，预测变量值相似）的记录。
  2. 对于分类，找出这些相似记录中哪一类是多数，并将该类别分配给新记录。
  3. 对于预测（也称作 KNN 回归），求出这些相似记录的平均值，并用该平均值作为新记录的预测值。

K-最近邻的关键术语

  • 邻居（Neighbor） 与另一条记录有相似预测变量值的记录。

  • 距离度量（Distance metrics） 用一个单一数值来衡量一条记录与另一条记录相距多远。

  • 标准化（Standardization） 减去均值并除以标准差。 同义词：归一化（Normalization）

  • z分数（z-score） 标准化后得到的值。

  • K 在最近邻计算中考虑的邻居数量。

KNN 是最简单的预测/分类技术之一：它不需要拟合模型（如回归中那样）。但这并不意味着使用 KNN 是一个自动化的过程。预测结果取决于特征如何缩放、如何衡量相似性以及K设置得有多大。此外，所有预测变量都必须是数值形式。我们将通过一个分类示例来演示如何使用 KNN 方法。

一个小例子：预测贷款违约

表6-1显示了来自 LendingClub 的一些个人贷款数据记录。LendingClub 是P2P借贷领域的领导者，投资者群体向个人提供贷款。分析的目标是预测一笔新的潜在贷款的结果：已还清还是违约。

T6.1

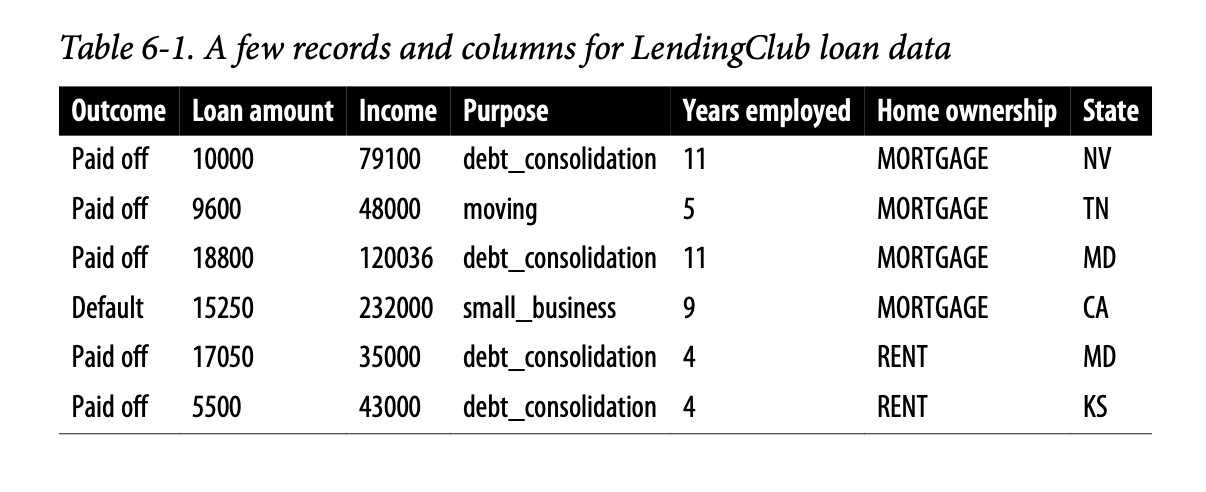
考虑一个非常简单的模型，只有两个预测变量：dti，即债务支付（不包括抵押贷款）与收入的比率；以及 payment_inc_ratio，即贷款还款额与收入的比率。两个比率都乘以100。

使用一个包含200笔贷款的小数据集 loan200，其中包含已知的二元结果（违约或未违约，在预测变量 outcome200 中指定），并将 K 设置为20。对于一笔待预测的新贷款 newloan，其 dti=22.5，payment_inc_ratio=9，KNN 估计值在 R 中可计算如下：

1
2
3
4
newloan <- loan200[1, 2:3, drop=FALSE]
knn_pred <- knn(train=loan200[-1, 2:3], test=newloan, cl=loan200[-1, 1], k=20)
knn_pred == 'paid off'
[1] TRUE

KNN 的预测结果是该贷款将会违约。

虽然 R 有一个原生的 knn 函数，但贡献的 R 包 FNN（意为 Fast Nearest Neighbor，快速最近邻）能更有效地扩展到大数据，并提供更大的灵活性。

scikit-learn 包在 Python 中提供了 KNN 的快速高效实现：

1
2
3
4
5
6
7
8
predictors = ['payment_inc_ratio', 'dti']
outcome = 'outcome'
newloan = loan200.loc[0:0, predictors]
X = loan200.loc[1:, predictors]
y = loan200.loc[1:, outcome]
knn = KNeighborsClassifier(n_neighbors=20)
knn.fit(X, y)
knn.predict(newloan)

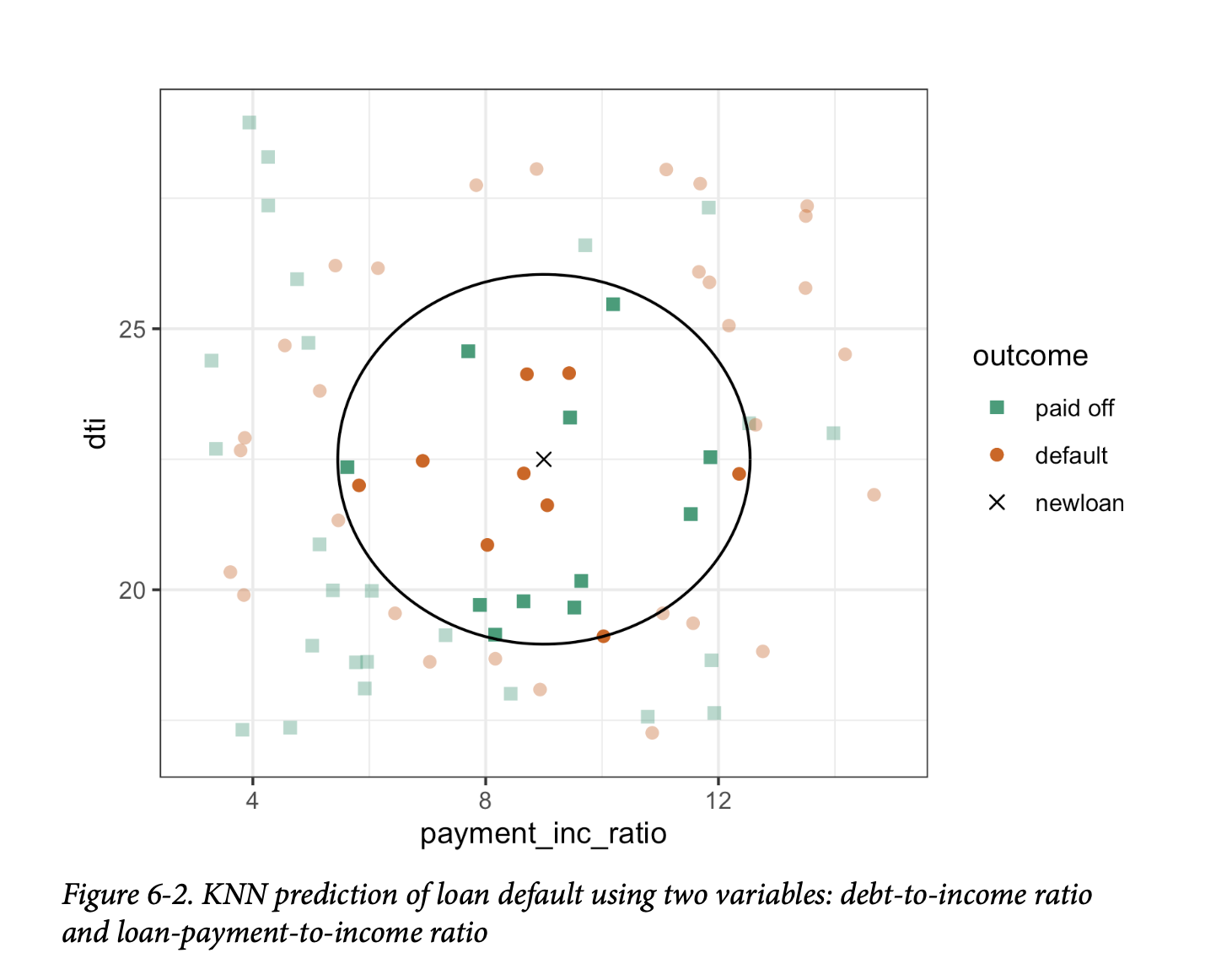
图6-2给出了这个例子的可视化展示。 . 中间的十字是待预测的新贷款。方块（已还清）和圆圈（违约）是训练数据。大黑圈显示了最近20个点的边界。在这个例子中，圆圈内有9笔违约贷款和11笔已还清贷款。因此，预测的贷款结果是已还清。注意，如果我们只考虑3个最近邻，预测结果将是贷款违约。

F6.2

通用注解：

KNN 分类的输出通常是一个二元决策，例如贷款数据中的违约或已还清，但KNN程序通常也提供输出一个介于0到1之间的概率（倾向性）。这个概率是基于K个最近邻居中某一类别所占的比例。在前面的例子中，违约的概率估计为\({9}/{20}\)，即0.45。

使用概率得分可以让您使用不同于简单多数投票（概率0.5）的分类规则。这在处理不平衡类别问题时尤为重要；参见第230页的“不平衡数据的策略”。例如，如果目标是识别一个罕见类别的成员，截止点通常会设置在50%以下。一种常见的方法是将截止点设置为罕见事件的发生概率。

距离度量

Distance Metrics

相似性（接近度）是使用距离度量来确定的，距离度量是一个函数，它测量两条记录 \((x_1, x_2, \dots, x_p)\) 和 \((u_1, u_2, \dots, u_p)\) 之间的距离。

两个向量之间最流行的距离度量是欧几里得距离（Euclidean distance）。要测量两个向量之间的欧几里得距离，需要将一个向量的对应分量减去另一个向量的对应分量，将差值平方，然后求和，最后取平方根：

\[ \sqrt{(x_1 - u_1)^2 + (x_2 - u_2)^2 + \cdots + (x_p - u_p)^2} \] 另一种用于数值数据的常见距离度量是曼哈顿距离（Manhattan distance）：

\[ |x_1 - u_1| + |x_2 - u_2| + \cdots + |x_p - u_p| \] 欧几里得距离对应于两点之间的直线距离（例如，像乌鸦飞行的距离）。曼哈顿距离是沿着单一方向一次移动一段距离来遍历两点之间的距离（例如，沿着矩形城市街区行进）。因此，如果相似性被定义为点到点的旅行时间，曼哈顿距离是一个有用的近似值。

在测量两个向量之间的距离时，测量尺度相对较大的变量（特征）将主导整个度量。例如，对于贷款数据，距离几乎完全取决于以成千上万计的收入和贷款金额变量。相比之下，比率变量的作用几乎可以忽略不计。我们通过标准化数据来解决这个问题；参见第243页的“标准化（归一化、z-分数）”。

通用注解：

其他距离度量（Other Distance Metrics）

有许多其他的度量方法可以用来测量向量之间的距离。对于数值数据，马氏距离（Mahalanobis distance）很有吸引力，因为它考虑了两个变量之间的相关性。这一点很有用，因为如果两个变量高度相关，马氏距离在计算时会本质上将它们视为一个单一变量。而欧几里得距离和曼哈顿距离不考虑相关性，实际上会更多地加权那些作为特征基础的属性。马氏距离是主成分（参见第284页的“主成分分析”）之间的欧几里得距离。使用马氏距离的缺点是增加了计算量和复杂性；它需要使用协方差矩阵进行计算（参见第202页的“协方差矩阵”）。

独热编码

One Hot Encoder

表6-1中的贷款数据包含几个因子（字符串）变量。大多数统计和机器学习模型要求将这类变量转换为一系列传达相同信息的二元虚拟变量，如表6-2所示。

T6.2

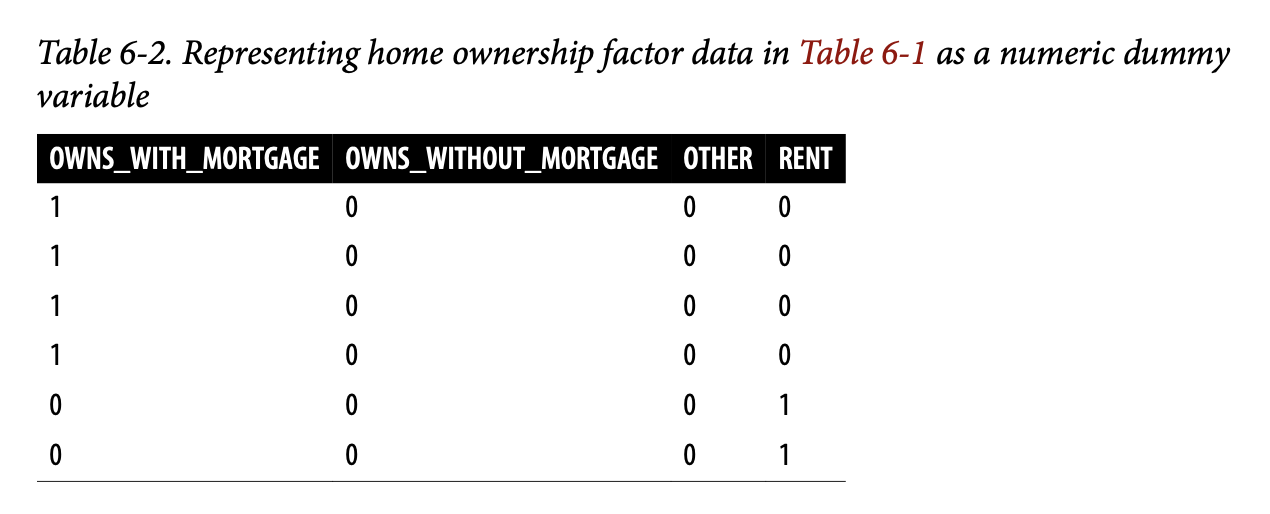
原本一个表示房产居住状态的单一变量，可以是“有抵押贷款自有房”、“无抵押贷款自有房”、“租房”或“其他”，现在我们得到了四个二元变量。第一个将是“有抵押贷款自有房 - 是/否”，第二个将是“无抵押贷款自有房 - 是/否”，以此类推。因此，这个名为“房产居住状态”的预测变量会产生一个包含一个1和三个0的向量，可用于统计和机器学习算法。独热编码（one hot encoding）这个短语源于数字电路术语，它描述的是一种电路设置，其中只有一个位被允许为正值（热）。

通用注解：

在线性回归和逻辑回归中，独热编码会引起多重共线性问题；参见第172页的“多重共线性”。在这种情况下，一个虚拟变量会被省略（它的值可以从其他变量推断出来）。但在KNN和本书讨论的其他方法中，这不是一个问题。

标准化（归一化，z-分数）

Standardization (Normalization, z-Scores)

在测量中，我们通常不那么关心“有多少”，而更关心“与平均值有多大差异”。标准化（Standardization），也称为归一化（Normalization），通过减去均值并除以标准差，将所有变量置于相似的尺度上；这样，我们确保一个变量不会仅仅因为其原始测量的尺度而过度影响模型：

\[ z = \frac{x - \bar{x}}{s} \] 这种转换的结果通常被称为 z-分数。测量值随后以“偏离均值的标准差”来表示。

警告：

在这种统计背景下的“归一化”不应与数据库归一化相混淆，后者是移除冗余数据和验证数据依赖关系的过程。

对于KNN和一些其他程序（例如主成分分析和聚类），在应用程序之前对数据进行标准化至关重要。为了说明这个想法，我们使用 dti 和 payment_inc_ratio（参见第239页的“一个小例子：预测贷款违约”）以及另外两个变量来对贷款数据应用KNN：revol_bal，申请人可用的总循环信贷余额（以美元计），以及 revol_util，已使用的信贷百分比。待预测的新记录如下所示：

1
2
3
newloan
payment_inc_ratio dti revol_bal revol_util
1 2.3932 1 1687 9.4

在revol_bal这个以美元计量的变量上，其量级远大于其他变量。knn函数返回最近邻居的索引作为一个属性nn.index，我们可以用它来展示loan_df中五个最接近的行：

1
2
3
4
5
6
7
loan_df <- model.matrix(~ -1 + payment_inc_ratio + dti + revol_bal +
revol_util, data=loan_data)
newloan <- loan_df[1, , drop=FALSE]
loan_df <- loan_df[-1,]
outcome <- loan_data[-1, 1]
knn_pred <- knn(train=loan_df, test=newloan, cl=outcome, k=5)
loan_df[attr(knn_pred, "nn.index"),]
1
2
3
4
5
6
   payment_inc_ratio   dti   revol_bal   revol_util
35537          1.47212  1.46        1686       10.0
33652          3.38178  6.37        1688        8.4
25864          2.36303  1.39        1691        3.5
42954          1.28160  7.14        1684        3.9
43600          4.12244  8.98        1684        7.2

在模型拟合后，我们可以使用scikit-learn的kneighbors方法来识别训练集中五个最接近的行：

1
2
3
4
5
6
7
8
9
predictors = ['payment_inc_ratio', 'dti', 'revol_bal', 'revol_util']
outcome = 'outcome'
newloan = loan_data.loc[0:0, predictors]
X = loan_data.loc[1:, predictors]
y = loan_data.loc[1:, outcome]
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X, y)
nbrs = knn.kneighbors(newloan)
X.iloc[nbrs[1][0], :]

在这些邻居中，revol_bal的值与新记录中的值非常接近，但其他预测变量的值则完全不相干，基本上没有在确定邻居的过程中起到任何作用。

现在，我们比较一下将KNN应用于标准化后的数据，使用R的scale函数，该函数计算每个变量的z-分数：

1
2
3
4
5
6
7
8
9
loan_df <- model.matrix(~ -1 + payment_inc_ratio + dti + revol_bal +
revol_util, data=loan_data)
loan_std <- scale(loan_df)
newloan_std <- loan_std[1, , drop=FALSE]
loan_std <- loan_std[-1,]
loan_df <- loan_df[-1,]
outcome <- loan_data[-1, 1]
knn_pred <- knn(train=loan_std, test=newloan_std, cl=outcome, k=5)
loan_df[attr(knn_pred, "nn.index"),]
1
2
3
4
5
6
   payment_inc_ratio    dti    revol_bal   revol_util
2081          2.61091   1.03         1218        9.7
1439          2.34343   0.51          278        9.9
30216         2.71200   1.34         1075        8.5
28543         2.39760   0.74         2917        7.4
44738         2.34309   1.37          488        7.2

我们还需要移除loan_df的第一行，以使行号相互对应。

sklearn.preprocessing.StandardScaler方法首先使用预测变量进行训练，然后用于在训练KNN模型之前转换数据集：

1
2
3
4
5
6
7
8
9
10
11
newloan = loan_data.loc[0:0, predictors]
X = loan_data.loc[1:, predictors]
y = loan_data.loc[1:, outcome]
scaler = preprocessing.StandardScaler()
scaler.fit(X * 1.0)
X_std = scaler.transform(X * 1.0)
newloan_std = scaler.transform(newloan * 1.0)
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_std, y)
nbrs = knn.kneighbors(newloan_std)
X.iloc[nbrs[1][0], :]

五个最近的邻居在所有变量上都更加相似，这提供了一个更合理的结果。请注意，结果是以原始尺度显示的，但KNN是应用于缩放后的数据和待预测的新贷款的。

知识点：

使用z-分数只是重新缩放变量的一种方式。除了均值，我们还可以使用更稳健的位置估计量，例如中位数。同样，可以使用四分位距等不同的尺度估计量来代替标准差。有时，变量会被“压扁”到0-1的范围内。同样重要的是要意识到，将每个变量缩放到具有单位方差在某种程度上是武断的。这暗示着每个变量在预测能力上被认为具有相同的重要性。如果你主观上知道某些变量比其他变量更重要，那么可以对这些变量进行放大。例如，对于贷款数据，可以合理地预期还款与收入的比率非常重要。

通用注解：

标准化（归一化）并不会改变数据的分布形状；如果数据本身不呈正态分布，标准化也不会使其变为正态分布（参见第69页的“正态分布”）。

K的选择

Choosing K

K的选择对于KNN的性能非常重要。最简单的选择是设置K = 1，这被称为1-最近邻分类器。它的预测很直观：基于在训练集中找到与待预测新记录最相似的数据记录。但是，将K设置为1很少是最佳选择；通常情况下，使用K>1的最近邻居会获得更好的性能。

一般来说，如果K过低，我们可能会过拟合：包含了数据中的噪声。较高的K值提供了平滑效果，可以降低训练数据过拟合的风险。另一方面，如果K过高，我们可能会过度平滑数据，并错过KNN捕捉数据局部结构的能力，而这正是其主要优势之一。

在过拟合和过度平滑之间取得最佳平衡的K值通常通过准确率指标来确定，特别是使用保留（holdout）或验证数据时的准确率。关于最佳K值没有普适的规则——它很大程度上取决于数据的性质。对于结构高度清晰且噪声较小的数据，较小的K值效果最好。借用信号处理领域的一个术语，这类数据有时被称为具有高信噪比（SNR）。手写和语音识别数据集就是通常具有高信噪比的例子。对于噪声大且结构较少的数据（低信噪比数据），例如贷款数据，较大的K值更合适。通常，K值在1到20之间。为了避免平局，通常会选择一个奇数。

通用注解：

偏差-方差权衡（Bias-Variance Trade-off）

过度平滑与过拟合之间的矛盾是偏差-方差权衡的一个例子，这是统计模型拟合中一个普遍存在的问题。

  • 方差指的是由于选择训练数据而产生的建模误差；也就是说，如果你选择一组不同的训练数据，得到的模型也会不同。
  • 偏差指的是由于你没有正确识别底层的真实世界情景而产生的建模误差；即使你简单地增加更多的训练数据，这种误差也不会消失。

当一个灵活的模型过拟合时，方差会增加。你可以通过使用一个更简单的模型来减少方差，但由于模型在模拟真实底层情况时失去了灵活性，偏差可能会增加。处理这种权衡的一种通用方法是交叉验证。有关更多细节，请参见第155页的“交叉验证”。

KNN作为特征引擎

KNN as a Feature Engine

KNN因其简单和直观的特性而受到欢迎。但在性能方面，KNN本身通常无法与更复杂的分类技术竞争。然而，在实际模型拟合中，可以通过分阶段的过程将KNN与其他分类技术结合，以添加“局部知识”：

  1. 对数据运行KNN，为每条记录得出一个分类（或一个类别的准概率）。
  2. 将这个结果作为一个新特征添加到记录中，然后用另一种分类方法对数据进行处理。这样，原始的预测变量就被使用了两次。

你可能首先会想，这个过程是否会因为某些预测变量被使用两次而导致多重共线性问题（参见第172页的“多重共线性”）。这不是一个问题，因为被纳入第二阶段模型的信息是高度局部的，它只来自少数几条附近的记录，因此是附加信息而非冗余信息。

通用注解：

你可以将这种分阶段使用KNN的方式看作是集成学习的一种形式，其中多个预测建模方法被结合在一起使用。它也可以被认为是特征工程的一种形式，其目的是推导出具有预测能力的特征（预测变量）。这通常需要手动审查数据；而KNN提供了一种相当自动化的方法来完成此任务。

例如，考虑金县（King County）的住房数据。在为待售房屋定价时，房地产经纪人会根据最近售出的类似房屋的价格来定价，这被称为“comps”（可比房屋）。从本质上讲，房地产经纪人正在进行手动版本的KNN：通过查看类似房屋的销售价格，他们可以估算出某一套房屋的售价。我们可以通过对最近的销售数据应用KNN，来为统计模型创建一个新特征，以模仿房地产专业人士的做法。预测值是销售价格，现有的预测变量可以包括位置、总平方英尺、结构类型、地块大小以及卧室和浴室的数量。我们通过KNN添加的新预测变量（特征）是每条记录的KNN预测值（类似于房地产经纪人的“comps”）。由于我们正在预测一个数值，这里使用的是K-最近邻的平均值而不是多数投票（这被称为KNN回归）。

类似地，对于贷款数据，我们可以创建代表贷款流程不同方面的新特征。例如，以下R代码将构建一个代表借款人信用度的特征：

1
2
3
4
5
6
7
borrow_df <- model.matrix(~ -1 + dti + revol_bal + revol_util + open_acc +
delinq_2yrs_zero + pub_rec_zero, data=loan_data)
borrow_knn <- knn(borrow_df, test=borrow_df, cl=loan_data[, 'outcome'],
prob=TRUE, k=20)
prob <- attr(borrow_knn, "prob")
borrow_feature <- ifelse(borrow_knn == 'default', prob, 1 - prob)
summary(borrow_feature)
1
2
   Min. 1st Qu. Median Mean 3rd Qu. Max.
0.000  0.400  0.500 0.501  0.600  0.950

使用 scikit-learn，我们使用训练模型的predict_proba方法来获取概率：

1
2
3
4
5
6
7
8
9
predictors = ['dti', 'revol_bal', 'revol_util', 'open_acc',
'delinq_2yrs_zero', 'pub_rec_zero']
outcome = 'outcome'
X = loan_data[predictors]
y = loan_data[outcome]
knn = KNeighborsClassifier(n_neighbors=20)
knn.fit(X, y)
loan_data['borrower_score'] = knn.predict_proba(X)[:, 1]
loan_data['borrower_score'].describe()

其结果是一个新特征，它根据借款人的信用历史来预测其违约的可能性。

关键思想

  • K-最近邻（KNN）通过将一条记录分配给与其相似的记录所属的类别来进行分类。
  • 相似性（距离）是通过欧几里得距离或其他相关度量来确定的。
  • 用于比较记录的最近邻居数量 K，是通过使用不同的K值来衡量算法在训练数据上的表现来确定的。
  • 通常，预测变量会进行标准化，以确保尺度较大的变量不会主导距离度量。
  • KNN常被用作预测建模的第一阶段，其预测值作为第二阶段（非KNN）建模的预测变量重新添加到数据中。

树模型

Tree Models

树模型，也称为分类与回归树（CART）、决策树，或简称树，是由 Leo Breiman 等人在1984年首次开发的一种有效且流行的分类（和回归）方法。树模型及其更强大的后代——随机森林和提升树（参见第259页的“装袋法与随机森林”和第270页的“提升法”）——构成了数据科学中最广泛使用和最强大的回归与分类预测建模工具的基础。

树的关键术语

  • 递归划分（Recursive partitioning） 反复地将数据进行划分和再划分，目的是使每个最终子划分中的结果尽可能同质（homogeneous）。

  • 分割值（Split value） 一个预测变量的值，它将记录分为两组：一组是该预测变量的值小于分割值的记录，另一组是大于分割值的记录。

  • 节点（Node） 在决策树或相应的分支规则集中，节点是分割值的图形或规则表示。

  • 叶子（Leaf） 一组if-then规则或树的分支的末端——将你带到该叶子的规则为树中的任何记录提供了一条分类规则。

  • 损失（Loss） 在分割过程的某个阶段中，错误分类的数量；损失越多，不纯度（impurity）越高。

  • 不纯度（Impurity） 数据子分区中各类别的混合程度（混合程度越高，不纯度越高）。 同义词：异质性（Heterogeneity） 反义词：同质性（Homogeneity）、纯度（purity）

  • 剪枝（Pruning） 对一棵完全生长的树进行逐步修剪其分支的过程，以减少过拟合。

树模型是一组“如果-那么-否则”的规则，易于理解和实现。与线性和逻辑回归相比，树模型能够发现数据中对应于复杂交互的隐藏模式。然而，与KNN或朴素贝叶斯不同的是，简单的树模型可以用易于解释的预测变量关系来表达。

警告：

运筹学中的决策树（Decision Trees in Operations Research）

在决策科学和运筹学中，“决策树”这个术语有一个不同（且更古老）的含义，它指的是一种人类决策分析过程。在这个含义下，决策点、可能的结果及其估计概率被呈现在一个分支图中，并选择具有最大预期价值的决策路径。

一个简单示例

A Simple Example

在 R 中拟合树模型主要有两个包：rpart 和 tree。使用 rpart 包，我们可以对3000条贷款数据记录的样本进行模型拟合，使用 payment_inc_ratio 和 borrower_score 变量（数据描述参见第238页的“K-最近邻”）：

1
2
3
4
5
library(rpart)
loan_tree <- rpart(outcome ~ borrower_score + payment_inc_ratio,
data=loan3000, control=rpart.control(cp=0.005))
plot(loan_tree, uniform=TRUE, margin=0.05)
text(loan_tree)

sklearn.tree.DecisionTreeClassifier 提供了决策树的实现。dmba 包提供了一个方便的函数，用于在Jupyter Notebook中创建可视化：

1
2
3
4
5
6
7
8
9
predictors = ['borrower_score', 'payment_inc_ratio']
outcome = 'outcome'
X = loan3000[predictors]
y = loan3000[outcome]
loan_tree = DecisionTreeClassifier(random_state=1, criterion='entropy',
min_impurity_decrease=0.003)
loan_tree.fit(X, y)
plotDecisionTree(loan_tree, feature_names=predictors,
class_names=loan_tree.classes_)

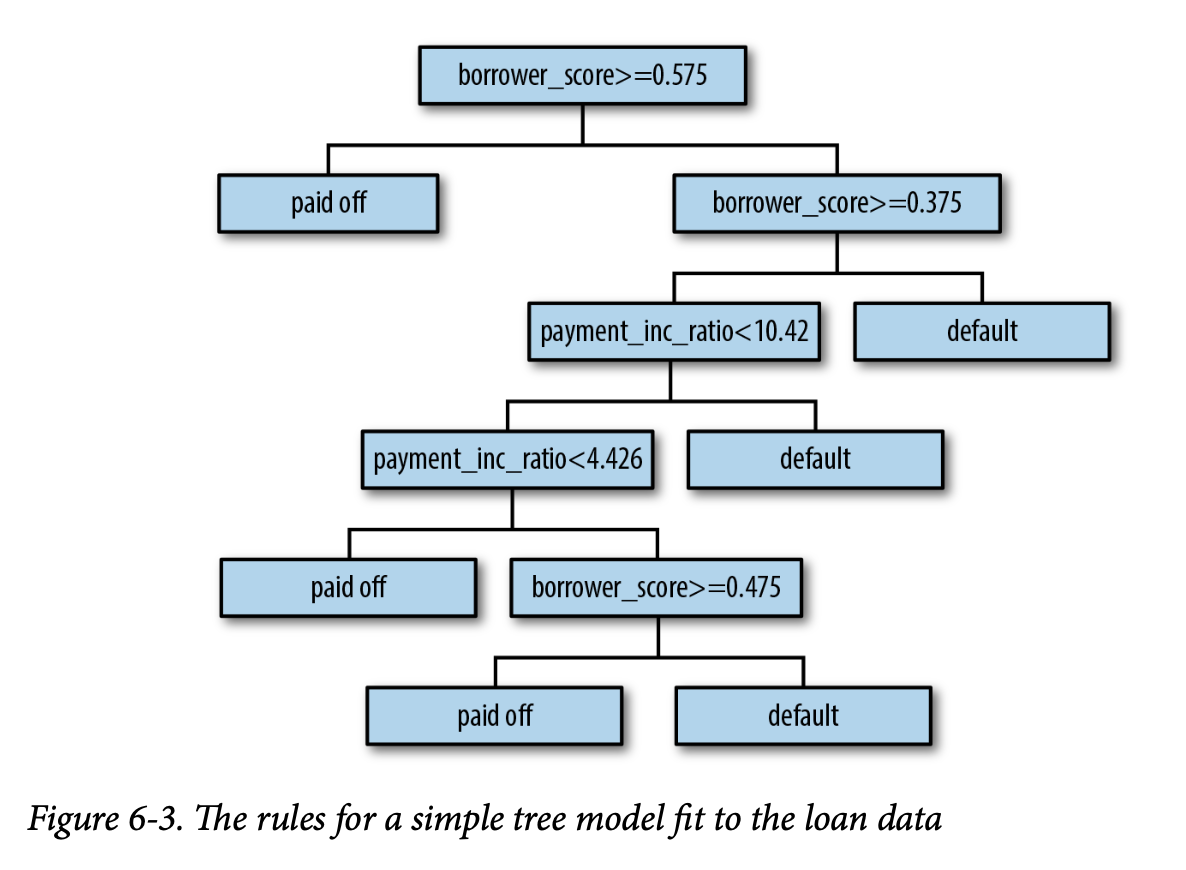
生成的树如图6-3所示。由于实现方式不同，你会发现 R 和 Python 的结果不完全相同；这是正常的。 . 这些分类规则是通过遍历一棵分层树来确定的，从根节点开始，如果节点条件为真则向左移动，否则向右移动，直到到达叶子节点。通常，树是倒置绘制的，根节点在顶部，叶子节点在底部。例如，如果一笔贷款的 borrower_score 为0.6，payment_inc_ratio 为8.0，我们最终会到达最左边的叶子节点，并预测该贷款将已还清。

F6.3

在 R 中也可以轻松生成一个格式优美的树文本版本：

1
loan_tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
n= 3000

node), split, n, loss, yval, (yprob)
      * denotes terminal node
1) root 3000 1445 paid off (0.5183333 0.4816667)
2) borrower_score>=0.575 878 261 paid off (0.7027335 0.2972665) *
3) borrower_score< 0.575 2122 938 default (0.4420358 0.5579642)
6) borrower_score>=0.375 1639 802 default (0.4893228 0.5106772)
12) payment_inc_ratio< 10.42265 1157 547 paid off (0.5272256 0.4727744)
24) payment_inc_ratio< 4.42601 334 139 paid off (0.5838323 0.4161677) *
25) payment_inc_ratio>=4.42601 823 408 paid off (0.5042527 0.4957473)
50) borrower_score>=0.475 418 190 paid off (0.5454545 0.4545455) *
51) borrower_score< 0.475 405 187 default (0.4617284 0.5382716) *
13) payment_inc_ratio>=10.42265 482 192 default (0.3983402 0.6016598) *
7) borrower_score< 0.375 483 136 default (0.2815735 0.7184265) *

树的深度由缩进表示。每个节点对应于由该分区中主要结果决定的临时分类。“损失”（loss）是在一个分区中，由该临时分类产生的错误分类数量。例如，在节点2中，总共878条记录中有261条是错误分类的。括号中的值分别对应于已还清贷款和违约贷款的比例。例如，在预测为违约的节点13中，超过60%的记录是违约贷款。

scikit-learn 文档描述了如何创建决策树模型的文本表示。我们在 dmba 包中包含了一个方便的函数：

1
print(textDecisionTree(loan_tree))
1
2
3
4
5
6
7
8
9
10
11
12
--
node=0 test node: go to node 1 if 0 <= 0.5750000178813934 else to node 6
node=1 test node: go to node 2 if 0 <= 0.32500000298023224 else to node 3
node=2 leaf node: [[0.785, 0.215]]
node=3 test node: go to node 4 if 1 <= 10.42264986038208 else to node 5
node=4 leaf node: [[0.488, 0.512]]
node=5 leaf node: [[0.613, 0.387]]
node=6 test node: go to node 7 if 1 <= 9.19082498550415 else to node 10
node=7 test node: go to node 8 if 0 <= 0.7249999940395355 else to node 9
node=8 leaf node: [[0.247, 0.753]]
node=9 leaf node: [[0.073, 0.927]]
node=10 leaf node: [[0.457, 0.543]]

递归划分算法

The Recursive Partitioning Algorithm

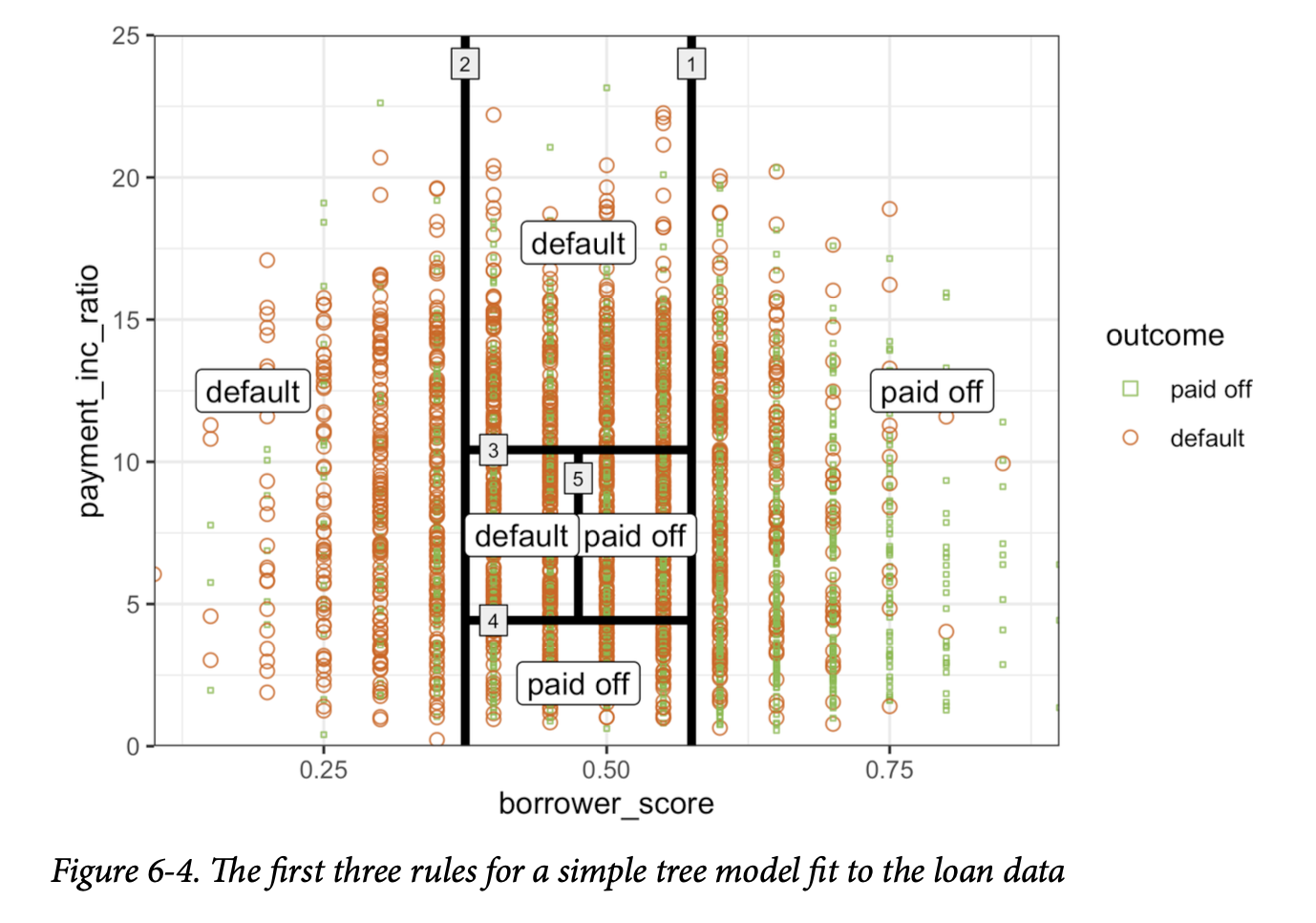
用于构建决策树的算法，称为递归划分，简单直观。该算法反复使用最能将数据划分为相对同质分区的预测变量值来对数据进行划分。图6-4展示了图6-3中树创建的分区。第一个规则（用规则1表示）是 borrower_score >= 0.575，它将图的右侧部分分割出来。第二个规则是 borrower_score < 0.375，它将左侧部分分割出来。

F6.4

假设我们有一个响应变量 \(Y\) 和一组 \(P\) 个预测变量 \(X_j\) (其中 \(j=1, \dots, P\))。对于一个记录分区 \(A\)，递归划分会找到最佳方式将其划分为两个子分区：

  1. 对于每个预测变量 \(X_j\)：
    1. 对于 \(X_j\) 的每个值 \(s_j\)：
      1. 将分区 \(A\) 中 \(X_j\) 值小于 \(s_j\) 的记录作为一个分区，其余 \(X_j\) 值大于或等于 \(s_j\) 的记录作为另一个分区。
      2. 测量 \(A\) 的每个子分区内类别的同质性。
    2. 选择能产生最大分区内类别同质性的 \(s_j\) 值。
  2. 选择能产生最大分区内类别同质性的变量 \(X_j\) 和分割值 \(s_j\)。

现在是递归部分： 1. 用整个数据集初始化 \(A\)。 2. 应用划分算法将 \(A\) 划分为两个子分区 \(A_1\) 和 \(A_2\)。 3. 对子分区 \(A_1\) 和 \(A_2\) 重复步骤2。 4. 当无法再进行能够充分改善分区同质性的划分时，算法终止。

最终结果是对数据的划分，如在\(P\)维空间中的图6-4所示，每个分区根据该分区中响应变量的多数投票来预测结果为0或1。

通用注解：

除了二元0/1预测，树模型还可以根据分区中0和1的数量来产生概率估计。该估计值就是分区中1的数量除以该分区中的观察记录总数： \[ P(Y=1) = \frac{分区中1的数量}{分区的大小} \] 然后，估计的 \(P(Y=1)\) 可以转换为二元决策；例如，如果 \(P(Y=1) > 0.5\)，则将估计值设为1。

测量同质性或不纯度

Measuring Homogeneity or Impurity

树模型会递归地创建分区（记录集）\(A\)，并预测结果 \(Y=0\) 或 \(Y=1\)。从前面的算法中可以看出，我们需要一种方法来测量分区内的同质性，也称为类别纯度。或者等价地，我们需要测量分区中的不纯度。预测的准确率是该分区内被错误分类的记录比例 \(p\)，其范围从0（完美）到0.5（纯随机猜测）。

事实证明，准确率不是一个好的不纯度度量。相反，两个常见的不纯度度量是 Gini不纯度（Gini impurity）和信息熵（entropy of information）。虽然这些（以及其他）不纯度度量也适用于具有两个以上类别的分类问题，但我们这里重点关注二元情况。

一个记录集 \(A\) 的 Gini不纯度是：

\[ I_G(A) = p(1 - p) \]

熵度量由下式给出：

\[ I_E(A) = -p \log_2 p - (1-p) \log_2 (1-p) \]

图6-5显示，基尼不纯度（重新缩放后）和熵度量是相似的，但熵对于中等到高准确率会给出更高的不纯度分数。

F6.5

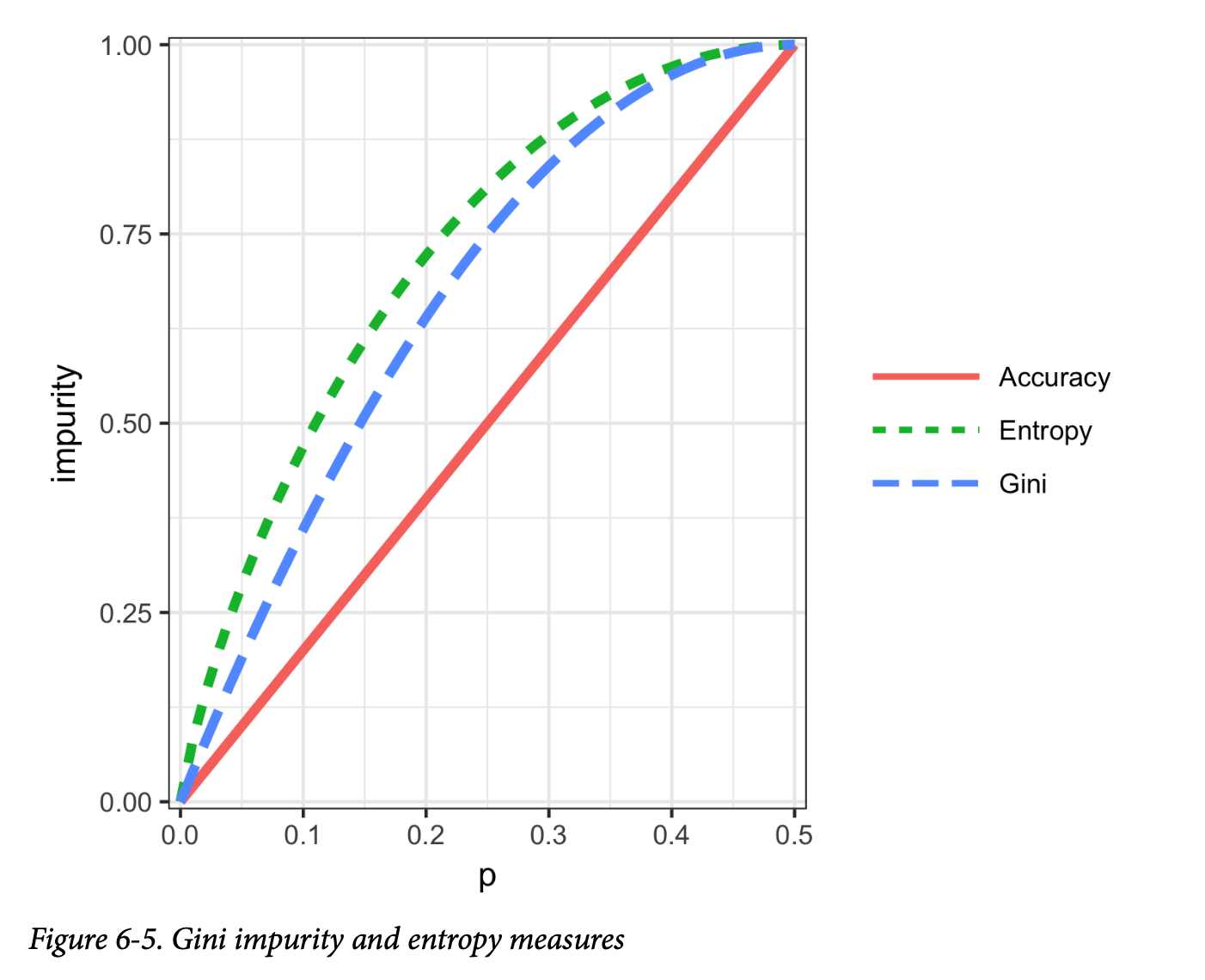
警告：

Gini系数

Gini不纯度不应与Gini系数相混淆。它们代表相似的概念，但Gini系数仅限于二元分类问题，并且与AUC指标相关（参见第226页的“AUC”）。

不纯度度量被用于前面描述的分割算法中。对于数据的每一个提议分区，都会测量由该分割所产生的每个分区的不纯度。然后计算一个加权平均值，并在每个阶段选择产生最低加权平均值的分区。

阻止树继续生长

Stopping the Tree from Growing

随着树变得越来越大，其分割规则也变得越来越详细，树会逐渐从识别数据中真实可靠的“大”规则，转变为反映噪声的“微小”规则。一棵完全生长的树会导致完全纯净的叶子，因此在分类其所训练的数据时会达到100%的准确率。当然，这种准确率是虚幻的——我们过拟合了数据（参见第247页的“偏差-方差权衡”），拟合的是训练数据中的噪声，而不是我们想要在新数据中识别的信号。

我们需要某种方法来决定何时停止树的生长，使其处于一个能够泛化到新数据的阶段。在R和Python中有多种方法可以阻止分割：

  • 如果生成的子分区太小，或终端叶子太小，就避免进行分割。 在 rpart (R) 中，这些约束分别由参数 minsplit 和 minbucket 控制，默认值分别为20和7。在 Python 的 DecisionTreeClassifier 中，我们可以使用参数 min_samples_split (默认2) 和 min_samples_leaf (默认1) 来控制。
  • 如果新的分区不能“显著”减少不纯度，则不进行分割。 在 rpart 中，这由复杂度参数 cp 控制，cp 是衡量树复杂度的指标——复杂度越高，cp 值越大。实际上，cp 被用来通过对树中额外的复杂度（分割）施加惩罚来限制树的生长。DecisionTreeClassifier (Python) 有一个参数 min_impurity_decrease，它根据加权不纯度减少值来限制分割。在这个参数中，较小的值将导致更复杂的树。

这些方法涉及主观规则，可以用于探索性工作，但我们不容易确定其最佳值（即，能最大化在新数据上的预测准确率的值）。我们需要将交叉验证与系统性地改变模型参数或通过剪枝来修改树的方法相结合。

在 R 中控制树的复杂度

利用复杂度参数 cp，我们可以估计出哪种大小的树在新数据上表现最佳。如果 cp 太小，树就会过拟合数据，拟合了噪声而非信号。另一方面，如果 cp 太大，树就会太小，预测能力也会很弱。rpart 的默认值为0.01，不过对于大型数据集来说，这个值可能太大。在前面的例子中，我们将 cp 设置为0.005，因为默认值导致了只有一个分割的树。在探索性分析中，简单地尝试几个值就足够了。

确定最佳 cp 值是偏差-方差权衡的一个例子。估算一个好的 cp 值的最常用方法是通过交叉验证（参见第155页的“交叉验证”）： 1. 将数据划分为训练集和验证集（保留集）。 2. 用训练数据生长树。 3. 逐步修剪它，在每一步记录 cp 值（使用训练数据）。 4. 记录对应于验证数据上最小误差（损失）的 cp 值。 5. 重新将数据划分为训练集和验证集，并重复树的生长、修剪和 cp 值记录过程。 6. 反复执行此操作，并对每棵树反映最小误差的 cp 值取平均。 7. 回到原始数据或未来的数据上，生长一棵树，并在最佳 cp 值处停止。

在 rpart 中，您可以使用参数 cptable 生成一个包含 cp 值及其相关交叉验证误差（在 R 中为 xerror）的表格，您可以从中确定具有最低交叉验证误差的 cp 值。

在 Python 中控制树的复杂度

在 scikit-learn 的决策树实现中，既没有复杂度参数，也没有剪枝功能。解决方案是使用网格搜索来组合不同的参数值。例如，我们可以将 max_depth 的范围设为5到30，min_samples_split 在20到100之间变化。scikit-learn 中的 GridSearchCV 方法是一种方便的方式，可以将穷尽搜索所有组合与交叉验证结合起来。然后，根据交叉验证的模型性能选择最优参数集。

预测连续值

Predicting a Continuous Value

用树模型预测连续值（也称为回归）遵循同样的逻辑和程序，只是不纯度的测量方式不同。在每个子分区中，不纯度是通过与均值的平方偏差（平方误差）来测量的，并且预测性能是根据每个分区中均方根误差（RMSE）的平方根来评估的（参见第153页的“评估模型”）。

scikit-learn 提供了 sklearn.tree.DecisionTreeRegressor 方法来训练决策树回归模型。

树模型的应用方式

How Trees Are Used

组织中预测建模人员面临的一大障碍是，他们所使用的方法被认为是“黑箱”，这会引起组织内其他部门的反对。在这方面，树模型有两个吸引人的优点：

  • 树模型提供了一个可视化工具来探索数据，从而了解哪些变量是重要的，以及它们之间是如何相互关联的。树可以捕捉预测变量之间的非线性关系。
  • 树模型提供了一套规则，可以有效地传达给非专业人士，以便进行实施或“推销”数据挖掘项目。

然而，在预测方面，利用多个树的结果通常比只使用单个树更强大。特别是，随机森林和提升树算法几乎总是提供卓越的预测准确性和性能（参见第259页的“装袋法与随机森林”和第270页的“提升法”），但单个树的上述优点也随之丧失了。

关键思想

  • 决策树生成一系列规则，用于分类或预测结果。
  • 这些规则对应于对数据进行连续的分区。
  • 每个分区或分割都引用一个特定的预测变量值，并将数据分为该预测变量值高于或低于该分割值的记录。
  • 在每个阶段，树算法选择能够最小化每个子分区内结果不纯度的分割点。
  • 当无法再进行分割时，树就完全生长了，每个终端节点或叶子节点都只包含单一类别的记录；遵循该规则（分割）路径的新案例将被分配到该类别。
  • 一棵完全生长的树会过拟合数据，必须进行剪枝，以使其捕捉信号而非噪声。
  • 多树算法，如随机森林和提升树，能提供更好的预测性能，但它们失去了单棵树基于规则的可沟通能力。

装袋法与随机森林

Bagging and the Random Forest

1906年，统计学家弗朗西斯·高尔顿爵士参观英格兰的一个乡村集市，那里正在举行一场猜测展览公牛净重的比赛。共有800个猜测，尽管单个猜测差异很大，但其平均值和中位数与公牛的真实重量相差不到1%。詹姆斯·苏洛维基在他的著作《群体的智慧》（The Wisdom of Crowds, Doubleday, 2004）中探讨了这一现象。这一原理也适用于预测模型：对多个模型进行平均（或多数投票）——即模型集成——结果证明比仅选择一个模型更为准确。

装袋法与随机森林的关键术语

  • 集成（Ensemble） 通过使用一组模型来形成预测。 同义词：模型平均（Model averaging）

  • 装袋法（Bagging） 一种通过对数据进行自举来形成一组模型的通用技术。 同义词：自举聚合（Bootstrap aggregation）

  • 随机森林（Random forest） 一种基于决策树模型的装袋估计方法。 同义词：装袋决策树（Bagged decision trees）

  • 变量重要性（Variable importance） 衡量预测变量在模型性能中的重要性的指标。

集成方法已被应用于许多不同的建模方法，最著名的例子是Netflix Prize，Netflix曾悬赏100万美元，奖励任何能够将预测顾客对电影评分的准确性提高10%的参赛者。集成的简单版本如下： 1. 开发一个预测模型，并记录给定数据集的预测结果。 2. 在相同数据上为多个模型重复此步骤。 3. 对于每条待预测的记录，对其预测结果取平均值（或加权平均值，或多数投票）。

集成方法最系统且最有效地应用于决策树。集成树模型非常强大，可以帮助我们以相对较少的努力构建出优秀的预测模型。

除了简单的集成算法，集成模型还有两个主要变体：装袋法和提升法。在集成树模型中，它们分别被称为随机森林模型和提升树模型。本节重点介绍装袋法；提升法将在第270页的“提升法”中进行讨论。

Bagging 方法

Bagging，是“bootstrap aggregating”（自助聚合）的缩写，由 Leo Breiman 于1994年提出。假设我们有一个响应变量 \(Y\) 和 \(P\) 个预测变量 \(\mathbf{X} = (X_1, X_2, \dots, X_P)\)，以及 \(N\) 条记录。

Bagging 类似于集成学习的基本算法，不同之处在于，不是将不同的模型拟合到相同的数据上，而是将每个新模型拟合到一个自助（bootstrap）重采样的数据上。这里更正式地介绍该算法： 1. 初始化要拟合的模型数量 \(M\) 和要选择的记录数量 \(n\)（\(n < N\)）。设置迭代计数器 \(m=1\)。 2. 从训练数据中有放回地抽取 \(n\) 条记录，形成一个子样本 \(Y_m\) 和 \(\mathbf{X}_m\)（即“包”）。 3. 使用 \(Y_m\) 和 \(\mathbf{X}_m\) 训练一个模型，以创建一组决策规则 \(\hat f_m(\mathbf{X})\)。 4. 增加模型计数器 \(m = m + 1\)。如果 \(m \le M\)，返回步骤2。

在 \(\hat f_m\) 预测 \(Y=1\) 的概率的情况下，bagging 估计量由下式给出：

\[ \hat f(\mathbf{X}) = \frac{1}{M} (\hat f_1(\mathbf{X}) + \hat f_2(\mathbf{X}) + \dots + \hat f_M(\mathbf{X})) \]

随机森林

Random Forest

随机森林是在决策树上应用装袋法的一种重要扩展：除了对记录进行抽样，该算法也对变量进行抽样。在传统的决策树中，为了确定如何创建一个子分区 \(A\)，算法会通过最小化Gini不纯度等标准来选择变量和分割点（参见第254页的“测量同质性或不纯度”）。而在随机森林中，在算法的每个阶段，变量的选择被限制在一个随机的变量子集中。

与基本的树算法（参见第252页的“递归划分算法”）相比，随机森林算法增加了两个步骤：前面讨论过的装袋法（参见第259页的“装袋法与随机森林”），以及在每次分割时对变量进行的自举抽样：

  1. 从记录中进行自举（有放回）抽样。
  2. 对于第一次分割，无放回地随机抽取 \(p < P\) 个变量。
  3. 对于每个抽样的变量 \(X_{j_1}, X_{j_2}, \dots, X_{j_p}\)，应用分割算法：
    1. 对于每个 \(X_{j_k}\) 的值 \(s_{j_k}\)：
    2. 将分区 \(A\) 中 \(X_{j_k}\) 值小于 \(s_{j_k}\) 的记录划分为一个分区，其余 \(X_{j_k}\) 值大于或等于 \(s_{j_k}\) 的记录作为另一个分区。
    1. 测量 \(A\) 的每个子分区内的类别同质性。
    1. 选择能产生最大分区内类别同质性的 \(s_{j_k}\) 值。
  4. 选择能产生最大分区内类别同质性的变量 \(X_{j_k}\) 和分割值 \(s_{j_k}\)。
  5. 继续进行下一次分割，从步骤2开始重复之前的步骤。
  6. 继续进行额外的分割，遵循相同的程序，直到树完全生长。
  7. 回到步骤1，进行另一次自举子抽样，并重新开始整个过程。

在每一步中要抽取多少变量？经验法则是选择 \(\sqrt{P}\)，其中 \(P\) 是预测变量的数量。randomForest 包在 R 中实现了随机森林。以下代码将此包应用于贷款数据（数据描述参见第238页的“K-最近邻”）：

1
2
3
rf <- randomForest(outcome ~ borrower_score + payment_inc_ratio,
data=loan3000)
rf
1
2
3
4
5
6
7
8
9
10
11
12
Call:
 randomForest(formula = outcome ~ borrower_score + payment_inc_ratio,
 data = loan3000)
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 1

        OOB estimate of  error rate: 39.17%
Confusion matrix:
         default paid off class.error
default      873      572   0.39584775
paid off     603      952   0.38778135

在 Python 中，我们使用 sklearn.ensemble.RandomForestClassifier 方法：

1
2
3
4
5
6
predictors = ['borrower_score', 'payment_inc_ratio']
outcome = 'outcome'
X = loan3000[predictors]
y = loan3000[outcome]
rf = RandomForestClassifier(n_estimators=500, random_state=1, oob_score=True)
rf.fit(X, y)

默认情况下，会训练500棵树。由于预测变量集中只有两个变量，算法在每个阶段随机选择一个变量进行分割（即，大小为1的自举子样本）。

袋外误差（Out-of-bag, OOB） 是指训练好的模型应用于未被用于该树训练的数据时的误差率。利用模型的输出，可以在 R 中绘制OOB误差与随机森林中树的数量之间的关系图：

1
2
3
4
error_df = data.frame(error_rate=rf$err.rate[,'OOB'],
num_trees=1:rf$ntree)
ggplot(error_df, aes(x=num_trees, y=error_rate)) +
geom_line()

RandomForestClassifier 的实现没有简单的方法来获取作为随机森林中树数量函数的袋外估计。我们可以训练一系列树数量递增的分类器，并跟踪 oob_score_ 值。然而，这种方法效率不高：

1
2
3
4
5
6
7
8
9
n_estimator = list(range(20, 510, 5))
oobScores = []
for n in n_estimator:
rf = RandomForestClassifier(n_estimators=n, criterion='entropy',
max_depth=5, random_state=1, oob_score=True)
rf.fit(X, y)
oobScores.append(rf.oob_score_)
df = pd.DataFrame({ 'n': n_estimator, 'oobScore': oobScores })
df.plot(x='n', y='oobScore')

F6.6

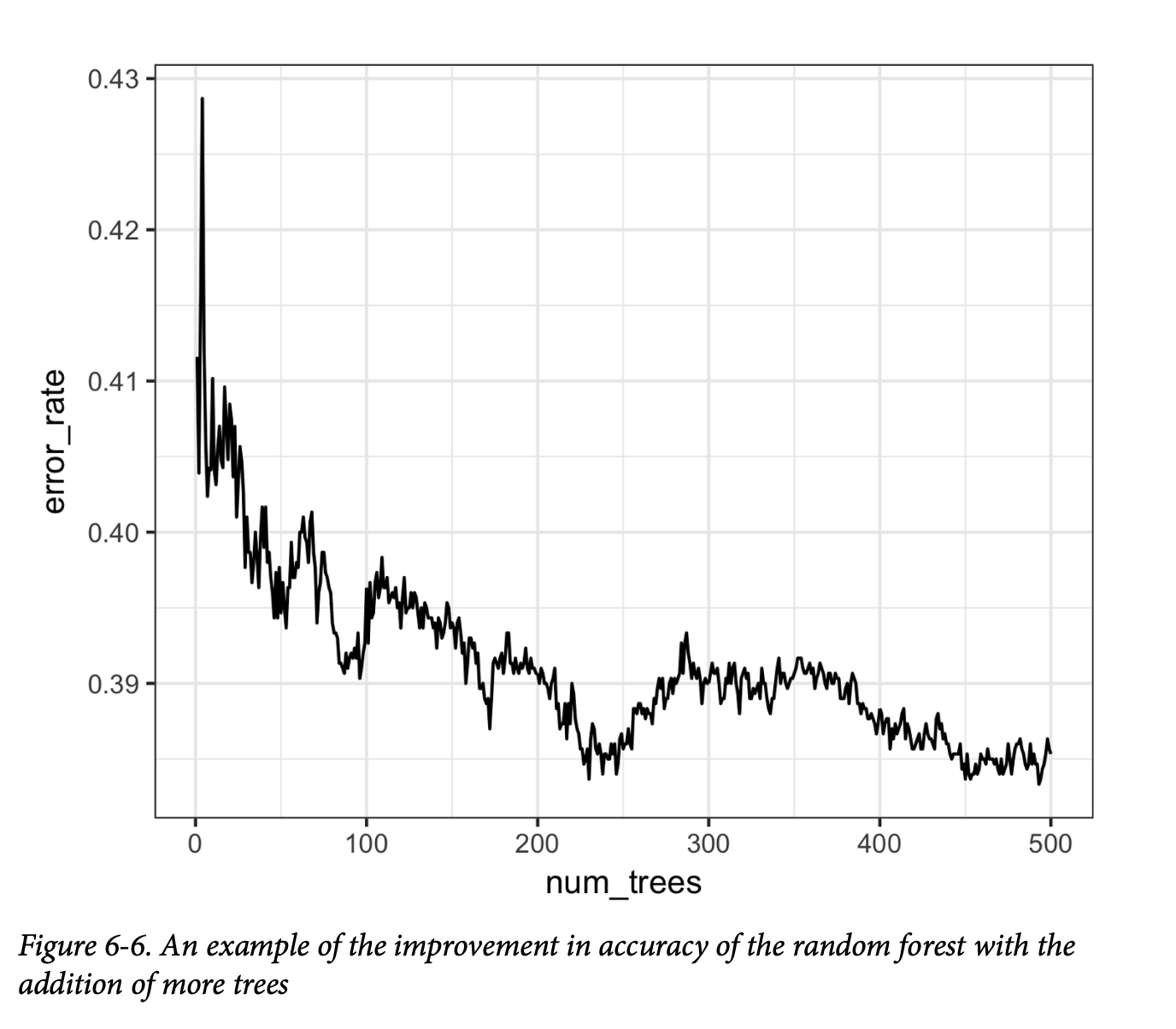
结果如图6-6所示。 误差率从超过0.44迅速下降，随后稳定在0.385左右。预测值可以通过 predict 函数获得，并在 R 中绘制如下：

1
2
3
4
5
6
7
8
pred <- predict(rf, prob=TRUE)
rf_df <- cbind(loan3000, pred = pred)
ggplot(data=rf_df, aes(x=borrower_score, y=payment_inc_ratio,
shape=pred, color=pred, size=pred)) +
geom_point(alpha=.8) +
scale_color_manual(values = c('paid off'='#b8e186', 'default'='#d95f02')) +
scale_shape_manual(values = c('paid off'=0, 'default'=1)) +
scale_size_manual(values = c('paid off'=0.5, 'default'=2))

在 Python 中，我们可以创建类似的图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
predictions = X.copy()
predictions['prediction'] = rf.predict(X)
predictions.head()
fig, ax = plt.subplots(figsize=(4, 4))
predictions.loc[predictions.prediction=='paid off'].plot(
x='borrower_score', y='payment_inc_ratio', style='.',
markerfacecolor='none', markeredgecolor='C1', ax=ax)
predictions.loc[predictions.prediction=='default'].plot(
x='borrower_score', y='payment_inc_ratio', style='o',
markerfacecolor='none', markeredgecolor='C0', ax=ax)
ax.legend(['paid off', 'default']);
ax.set_xlim(0, 1)
ax.set_ylim(0, 25)
ax.set_xlabel('borrower_score')
ax.set_ylabel('payment_inc_ratio')

该图（如图6-7所示）很好地揭示了随机森林的本质。

F6.7

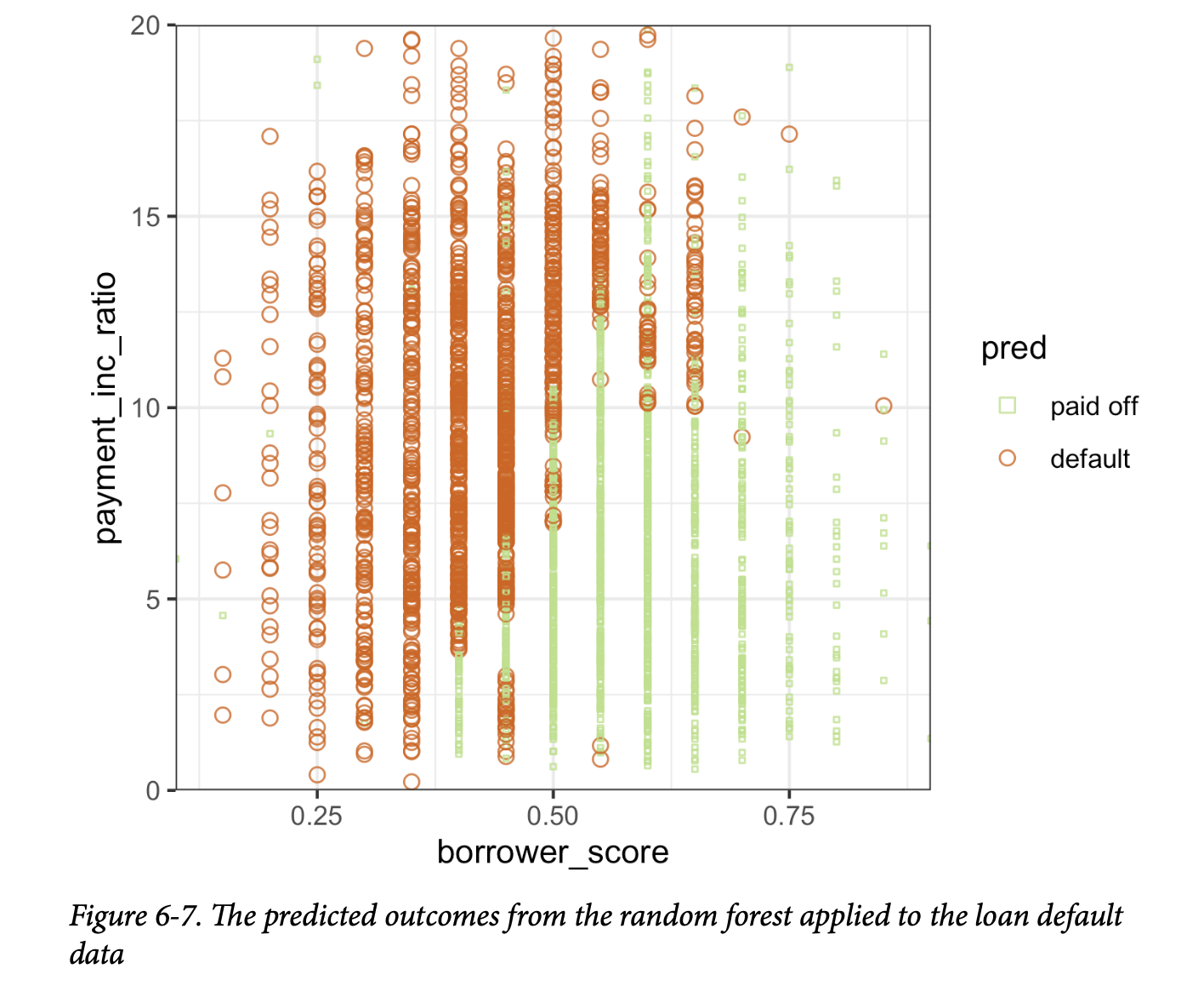
随机森林方法是一种“黑箱”方法。它比单个树产生更准确的预测，但单个树直观的决策规则却丢失了。随机森林的预测也有些噪声：请注意，一些借款人得分非常高（表明信用度高）的贷款，最终仍被预测为违约。这是数据中一些不寻常记录的结果，也展示了随机森林过拟合的危险（参见第247页的“偏差-方差权衡”）。

变量重要性

Variable Importance

当您为具有许多特征和记录的数据构建预测模型时，随机森林算法的强大之处就显现出来了。它能够自动确定哪些预测变量是重要的，并发现与交互项相对应的预测变量之间的复杂关系（参见第174页的“交互项与主效应”）。例如，使用所有列对贷款违约数据进行模型拟合。以下代码在 R 中展示了这一点：

1
2
3
rf_all <- randomForest(outcome ~
., data=loan_data, importance=TRUE)
rf_all
1
2
3
4
5
6
7
8
9
10
11
12
Call:
 randomForest(formula = outcome ~
., data = loan_data, importance = TRUE)
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 4

        OOB estimate of  error rate: 33.79%
Confusion matrix:
         paid off default class.error
paid off    14676    7995  0.3526532
default      7325   15346  0.3231000

在 Python 中：

1
2
3
4
5
6
7
8
9
predictors = ['loan_amnt', 'term', 'annual_inc', 'dti', 'payment_inc_ratio',
'revol_bal', 'revol_util', 'purpose', 'delinq_2yrs_zero',
'pub_rec_zero', 'open_acc', 'grade', 'emp_length', 'purpose_',
'home_', 'emp_len_', 'borrower_score']
outcome = 'outcome'
X = pd.get_dummies(loan_data[predictors], drop_first=True)
y = loan_data[outcome]
rf_all = RandomForestClassifier(n_estimators=500, random_state=1)
rf_all.fit(X, y)

importance=TRUE 参数要求 randomForest 存储关于不同变量重要性的额外信息。varImpPlot 函数将绘制变量的相对性能（相对于排列该变量）：

1
varImpPlot(rf_all, type=1)

mean decrease in accuracy

1
varImpPlot(rf_all, type=2)

mean decrease in node impurity

在 Python 中，RandomForestClassifier 在训练期间会收集特征重要性的信息，并通过 feature_importances_ 字段使其可用：

1
importances = rf_all.feature_importances_

分类器的 feature_importance_ 属性提供了“Gini 减少量”（Gini decrease）。然而，Python 中“准确率减少量”（Accuracy decrease）并非开箱即用。我们可以使用以下代码来计算它：

1
2
3
4
5
6
7
8
9
10
11
12
rf = RandomForestClassifier(n_estimators=500)
scores = defaultdict(list)
# cross-validate the scores on a number of different random splits of the data
for
_
in range(3):
train_X, valid_X, train_y, valid_y = train_test_split(X, y, test_size=0.3)
rf.fit(train_X, train_y)
acc = metrics.accuracy_score(valid_y, rf.predict(valid_X))
for column in X.columns:
X_t = valid_X.copy()
X_t[column] = np.random.permutation(X_t[column].values)

F6.8

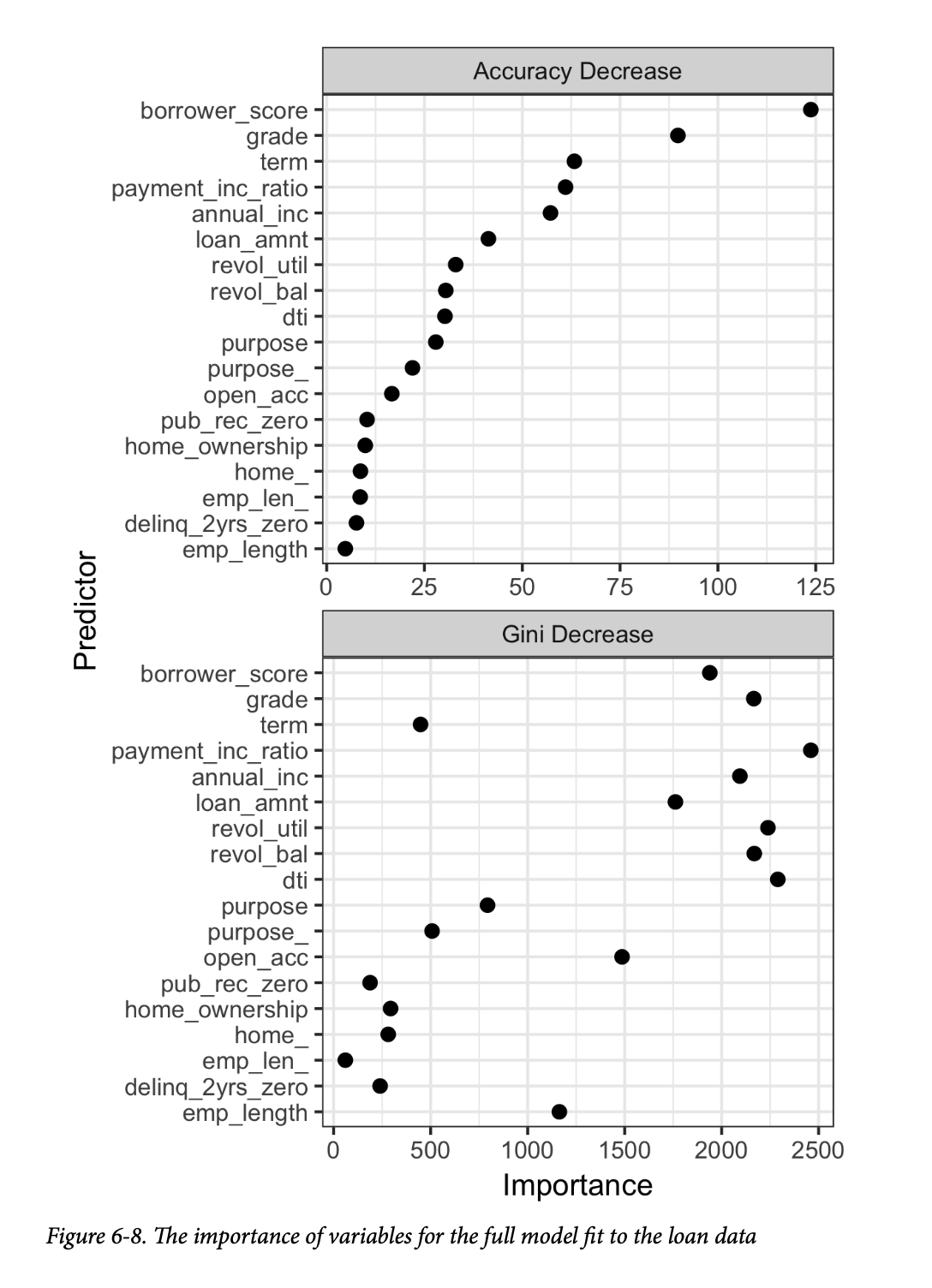
结果如图6-8所示。 类似的图表可以使用这段Python代码创建：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
df = pd.DataFrame({
'feature': X.columns,
'Accuracy decrease': [np.mean(scores[column]) for column in X.columns],
'Gini decrease': rf_all.feature_importances_,
})
df = df.sort_values('Accuracy decrease')
fig, axes = plt.subplots(ncols=2, figsize=(8, 4.5))
ax = df.plot(kind='barh', x='feature', y='Accuracy decrease',
legend=False, ax=axes[0])
ax.set_ylabel('')
ax = df.plot(kind='barh', x='feature', y='Gini decrease',
legend=False, ax=axes[1])
ax.set_ylabel('')
ax.get_yaxis().set_visible(False)

有两种方法来衡量变量重要性：

  • 通过模型准确率的减少量来衡量（type=1），当一个变量的值被随机排列时。随机排列这些值的作用是消除该变量的所有预测能力。准确率是从袋外数据（out-of-bag data）计算得出的（因此这个度量实际上是一个交叉验证估计）。
  • 通过所有节点 Gini不纯度评分的平均减少量来衡量（type=2），这些节点都曾根据该变量进行分割（参见第254页的“测量同质性或不纯度”）。这衡量了包含该变量能在多大程度上提高节点纯度。这个度量是基于训练集的，因此比在袋外数据上计算的度量更不可靠。

图6-8的顶部和底部面板分别显示了根据准确率减少量和Gini不纯度减少量计算出的变量重要性。两个面板中的变量都按准确率减少量进行了排名。这两种方法产生的变量重要性得分差异很大。

既然准确率减少量是一个更可靠的指标，为什么我们还要使用 Gini不纯度减少量呢？默认情况下，randomForest 只计算 Gini不纯度：Gini不纯度是算法的副产品，而按变量计算的模型准确率需要额外的计算（随机排列数据并对这些数据进行预测）。在计算复杂度很重要的场景中，例如在生产环境中需要拟合数千个模型时，额外的计算工作可能不值得。此外，Gini减少量能揭示随机森林使用了哪些变量来制定其分割规则（回想一下，这些信息在单棵树中很容易看到，但在随机森林中实际上丢失了）。

超参数

Hyperparameters

随机森林与许多统计机器学习算法一样，可以被视为一个“黑箱算法”，其内部有一些可调整的“旋钮”。这些“旋钮”被称为超参数（hyperparameters），它们是您在拟合模型之前需要设定的参数；它们不作为训练过程的一部分进行优化。虽然传统的统计模型也需要选择（例如，在回归模型中选择要使用的预测变量），但随机森林的超参数更为关键，尤其是在避免过拟合方面。特别是，随机森林的两个最重要的超参数是：

  • nodesize/min_samples_leaf 终端节点（树中的叶子）的最小大小。在 R 中，分类的默认值为1，回归的默认值为5。Python 的 scikit-learn 实现中，两者默认值均为1。

  • maxnodes/max_leaf_nodes 每个决策树中的最大节点数。默认情况下没有限制，将在 nodesize 约束下拟合最大尺寸的树。请注意，在 Python 中，您指定的是最大终端节点数。这两个参数之间存在关系：

    maxnodes = 2 * max_leaf_nodes - 1

您可能会很想忽略这些参数，直接使用默认值。然而，当您将随机森林应用于噪声数据时，使用默认值可能导致过拟合。当您增加 nodesize/min_samples_leaf 或设置 maxnodes/max_leaf_nodes 时，算法会拟合较小的树，从而更不容易创建虚假的预测规则。可以使用交叉验证（参见第155页的“交叉验证”）来测试设置不同超参数值所带来的影响。

关键思想

  • 集成模型通过结合多个模型的结果来提高模型准确率。
  • 装袋法是一种特殊的集成模型，它基于对数据的自举样本拟合多个模型并进行平均。
  • 随机森林是应用于决策树的一种特殊类型的装袋法。除了对数据进行重采样外，随机森林算法在分割树时还会对预测变量进行抽样。
  • 随机森林的一个有用输出是变量重要性的度量，它根据预测变量对模型准确率的贡献进行排名。
  • 随机森林有一组超参数，应使用交叉验证进行调优以避免过拟合。

提升法

Boosting

集成模型已成为预测建模的标准工具。提升法（Boosting）是一种创建模型集成的通用技术。它与装袋法（bagging）差不多是同时开发的（参见第259页的“装袋法与随机森林”）。与装袋法一样，提升法最常用于决策树。尽管它们有相似之处，但提升法采取了截然不同的方法——这种方法带有更多的“花哨功能”。因此，装袋法只需相对较少的调优即可完成，而提升法在其应用中需要更多的关注。如果将这两种方法比作汽车，装袋法可以被看作是本田雅阁（可靠且稳定），而提升法则可以被看作是保时捷（强大但需要更细心的呵护）。

在线性回归模型中，通常会检查残差以看是否可以改进拟合（参见第185页的“偏残差图和非线性”）。提升法将这个概念推向了更远，它拟合了一系列模型，其中每个后续模型都试图最小化前一个模型的误差。通常使用该算法的几个变体：Adaboost、梯度提升（gradient boosting）和随机梯度提升（stochastic gradient boosting）。后者，即随机梯度提升，是最通用和应用最广泛的。事实上，通过正确的参数选择，该算法可以模拟随机森林。

提升法的关键术语

  • 集成（Ensemble） 通过使用一系列模型来形成预测。 同义词：模型平均（Model averaging）

  • 提升法（Boosting） 一种通用技术，通过在每个连续轮次中对具有较大残差的记录赋予更多权重来拟合一系列模型。

  • Adaboost 提升法的早期版本，根据残差对数据进行重新加权。

  • 梯度提升（Gradient boosting） 一种更通用的提升形式，被定义为最小化成本函数。

  • 随机梯度提升（Stochastic gradient boosting） 最通用的提升算法，在每一轮中都包含了记录和列的重采样。

  • 正则化（Regularization） 一种通过在成本函数中添加惩罚项以避免模型过拟合的技术，该惩罚项与模型中的参数数量相关。

  • 超参数（Hyperparameters） 在拟合算法之前需要设定的参数。

提升算法

The Boosting Algorithm

提升算法有多种，但它们的基本思想本质上是相同的。最容易理解的是 Adaboost，它的过程如下：

  1. 初始化最大拟合模型数 \(M\)，并设置迭代计数器 \(m = 1\)。初始化观测权重 \(w_i = 1/N\)（对于 \(i=1, 2, \dots, N\)）。初始化集成模型 \(F_0 = 0\)。
  2. 使用观测权重 \(w_1, w_2, \dots, w_N\) 训练模型 \(\hat f_m\)，使其最小化加权误差 \(e_m\)，该误差由错误分类观测的权重总和定义。
  3. 将模型添加到集成中：\(\hat F_m = \hat F_{m-1} + \alpha_m \hat f_m\)，其中 \(\alpha_m = \log\frac{1 - e_m}{e_m}\)。
  4. 更新权重 \(w_1, w_2, \dots, w_N\)，以便增加被错误分类的观测的权重。增加的幅度取决于 \(\alpha_m\)，\(\alpha_m\) 的值越大，权重增加得越多。
  5. 递增模型计数器 \(m = m + 1\)。如果 \(m \le M\)，则返回步骤2。

提升后的估计值由下式给出：

\[ \hat F = \alpha_1 \hat f_1 + \alpha_2 \hat f_2 + \cdots + \alpha_M \hat f_M \] 通过增加被错误分类的观测的权重，该算法迫使模型更侧重于对其表现不佳的数据进行训练。因子 \(\alpha_m\) 确保误差较低的模型拥有更大的权重。

梯度提升与 Adaboost 类似，但它将问题视为成本函数的优化。梯度提升不是调整权重，而是拟合模型以适应伪残差，这起到了更侧重于较大残差进行训练的作用。

本着随机森林的精神，随机梯度提升通过在每个阶段对观测和预测变量进行抽样，为算法增加了随机性。

XGBoost

XGBoost

最广泛使用的用于提升法的开源软件是 XGBoost，它是由华盛顿大学的陈天奇和Carlos Guestrin最初开发的随机梯度提升的一种实现。它是一个计算高效且具有许多选项的实现，作为软件包可用于大多数主要的数据科学编程语言。在 R 中，XGBoost 可作为 xgboost 包使用，在 Python 中也使用相同的名称。

xgboost 方法有许多可以且应该调整的参数（参见第279页的“超参数与交叉验证”）。两个非常重要的参数是 subsample，它控制在每次迭代中应该采样的观测记录比例；以及 eta，一个应用于提升算法中 \(\alpha_m\) 的收缩因子（参见第271页的“提升算法”）。

使用 subsample 会让提升法的行为类似于随机森林，只是采样是无放回的。收缩参数 eta 有助于通过减少权重的变化来防止过拟合（权重的变化越小，算法就越不容易过拟合训练集）。

以下代码在 R 中将 xgboost 应用于只有两个预测变量的贷款数据：

1
2
3
4
predictors <- data.matrix(loan3000[, c('borrower_score', 'payment_inc_ratio')])
label <- as.numeric(loan3000[,'outcome']) - 1
xgb <- xgboost(data=predictors, label=label, objective="binary:logistic",
params=list(subsample=0.63, eta=0.1), nrounds=100)
1
2
3
4
5
6
[1] train-error:0.358333
[2] train-error:0.346333
[3] train-error:0.347333
...
[99] train-error:0.239333
[100] train-error:0.241000

请注意，xgboost 不支持公式语法，因此预测变量需要转换为 data.matrix，响应变量需要转换为0/1变量。objective 参数告诉 xgboost 这是哪种类型的问题；基于此，xgboost 会选择一个要优化的指标。

在 Python 中，xgboost 有两种不同的接口：scikit-learn API 和一个更像 R 的函数式接口。为了与其他 scikit-learn 方法保持一致，一些参数被重新命名了。例如，eta 被重命名为 learning_rate；使用 eta 虽然不会导致失败，但也不会产生预期的效果：

1
2
3
4
5
6
predictors = ['borrower_score', 'payment_inc_ratio']
outcome = 'outcome'
X = loan3000[predictors]
y = loan3000[outcome]
xgb = XGBClassifier(objective='binary:logistic', subsample=0.63)
xgb.fit(X, y)
1
2
3
4
5
6
7
--
XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bynode=1, colsample_bytree=1, gamma=0, learning_rate=0.1,
max_delta_step=0, max_depth=3, min_child_weight=1, missing=None,
n_estimators=100, n_jobs=1, nthread=None, objective='binary:logistic',
random_state=0, reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
silent=None, subsample=0.63, verbosity=1)

预测值可以从 R 中的 predict 函数获得，并且因为只有两个变量，可以针对预测变量进行绘制：

1
2
3
4
5
6
7
8
pred <- predict(xgb, newdata=predictors)
xgb_df <- cbind(loan3000, pred_default = pred > 0.5, prob_default = pred)
ggplot(data=xgb_df, aes(x=borrower_score, y=payment_inc_ratio,
color=pred_default, shape=pred_default, size=pred_default)) +
geom_point(alpha=.8) +
scale_color_manual(values = c('FALSE'='#b8e186', 'TRUE'='#d95f02')) +
scale_shape_manual(values = c('FALSE'=0, 'TRUE'=1)) +
scale_size_manual(values = c('FALSE'=0.5, 'TRUE'=2))

使用以下代码可以在 Python 中创建相同的图：

1
2
3
4
5
6
7
8
9
10
11
12
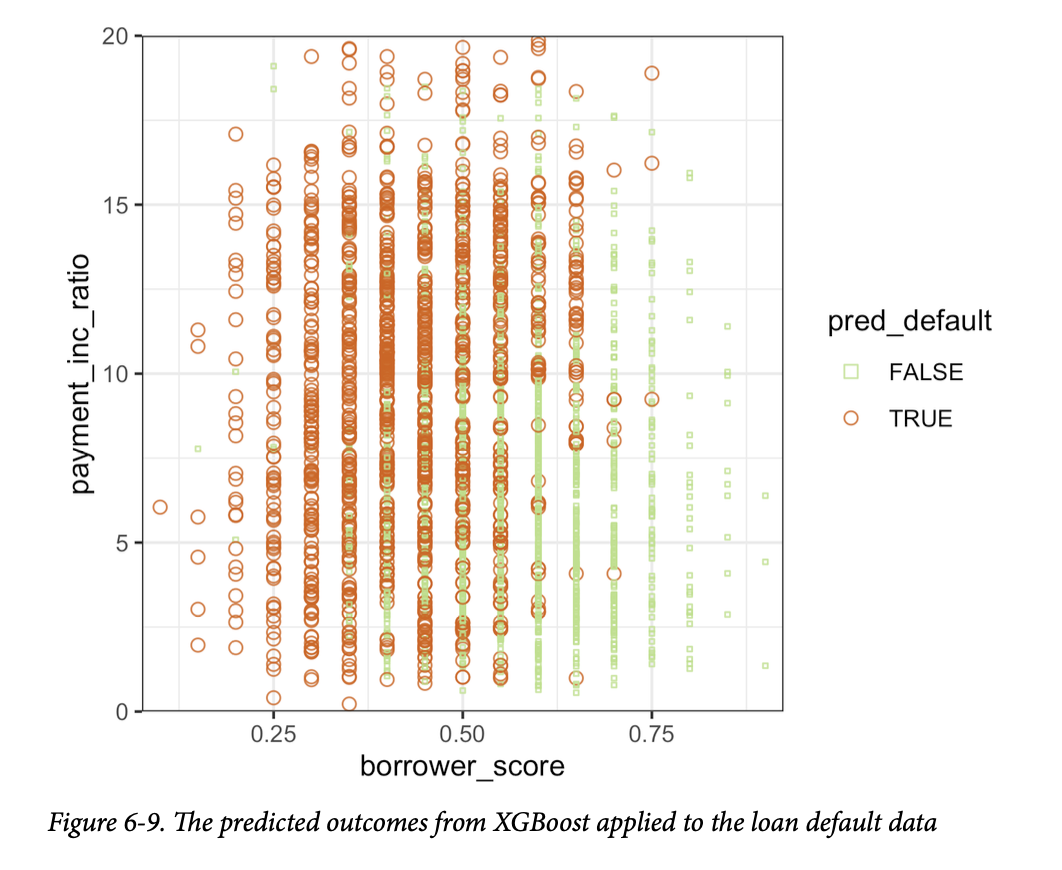
13
fig, ax = plt.subplots(figsize=(6, 4))
xgb_df.loc[xgb_df.prediction=='paid off'].plot(
x='borrower_score', y='payment_inc_ratio', style='.',
markerfacecolor='none', markeredgecolor='C1', ax=ax)

xgb_df.loc[xgb_df.prediction=='default'].plot(
x='borrower_score', y='payment_inc_ratio', style='o',
markerfacecolor='none', markeredgecolor='C0', ax=ax)
ax.legend(['paid off', 'default']);
ax.set_xlim(0, 1)
ax.set_ylim(0, 25)
ax.set_xlabel('borrower_score')
ax.set_ylabel('payment_inc_ratio')

结果如图6-9所示。 从定性上看，这与随机森林的预测结果相似；参见图6-7。预测结果有些噪声，因为一些借款人得分非常高（表明信用度高）的贷款，最终仍被预测为违约。

F6.9

正则化：避免过拟合

Regularization: Avoiding Overfitting

盲目应用 xgboost 可能会因过拟合训练数据而导致模型不稳定。过拟合问题是双重的：

  • 模型在不属于训练集的新数据上的准确率会降低。
  • 模型的预测高度可变，导致结果不稳定。

任何建模技术都可能容易过拟合。例如，如果回归方程中包含过多变量，模型最终可能会产生虚假预测。然而，对于大多数统计技术，通过明智地选择预测变量可以避免过拟合。即使是随机森林，通常在不调整参数的情况下也能产生一个合理的模型。

但是，xgboost 的情况并非如此。使用模型中包含的所有变量来拟合训练集上的贷款数据。在 R 中，您可以这样做：

1
2
3
4
5
6
7
8
9
10
11
seed <- 400820
predictors <- data.matrix(loan_data[, -which(names(loan_data) %in%
'outcome')])
label <- as.numeric(loan_data$outcome) - 1
test_idx <- sample(nrow(loan_data), 10000)
xgb_default <- xgboost(data=predictors[-test_idx,], label=label[-test_idx],
objective='binary:logistic', nrounds=250, verbose=0)
pred_default <- predict(xgb_default, predictors[test_idx,])
error_default <- abs(label[test_idx] - pred_default) > 0.5
xgb_default$evaluation_log[250,]
mean(error_default)
1
2
3
4
-
iter train_error
1: 250 0.133043
[1] 0.3529

我们使用 Python 中的 train_test_split 函数将数据集分为训练集和测试集：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
predictors = ['loan_amnt', 'term', 'annual_inc', 'dti', 'payment_inc_ratio',
'revol_bal', 'revol_util', 'purpose', 'delinq_2yrs_zero',
'pub_rec_zero', 'open_acc', 'grade', 'emp_length', 'purpose_',
'home_', 'emp_len_', 'borrower_score']
outcome = 'outcome'
X = pd.get_dummies(loan_data[predictors], drop_first=True)
y = pd.Series([1 if o == 'default' else 0 for o in loan_data[outcome]])
train_X, valid_X, train_y, valid_y = train_test_split(X, y, test_size=10000)
xgb_default = XGBClassifier(objective='binary:logistic', n_estimators=250,
max_depth=6, reg_lambda=0, learning_rate=0.3,
subsample=1)
xgb_default.fit(train_X, train_y)
pred_default = xgb_default.predict_proba(valid_X)[:, 1]

error_default = abs(valid_y - pred_default) > 0.5
print('default: ', np.mean(error_default))

测试集由从完整数据中随机抽样的10,000条记录组成，训练集则由剩余的记录组成。提升法在训练集上的错误率仅为13.3%。然而，测试集的错误率高达35.3%。这是过拟合的结果：虽然提升法可以很好地解释训练集中的可变性，但其预测规则不适用于新数据。

提升法提供了几个参数来避免过拟合，包括 eta (或 learning_rate) 和 subsample (参见第272页的“XGBoost”)。另一种方法是正则化，该技术通过添加一个惩罚模型复杂度的惩罚项来修改成本函数。决策树通过最小化 Gini不纯度评分等成本标准来进行拟合（参见第254页的“测量同质性或不纯度”）。在 xgboost 中，可以通过添加一个衡量模型复杂度的项来修改成本函数。

xgboost 中有两个用于正则化模型的参数：alpha 和 lambda，它们分别对应于曼哈顿距离（L1-正则化）和欧几里得距离平方（L2-正则化）（参见第241页的“距离度量”）。增加这些参数会惩罚更复杂的模型并减小拟合树的大小。例如，看看我们在 R 中将 lambda 设置为1000时会发生什么：

1
2
3
4
5
6
7
xgb_penalty <- xgboost(data=predictors[-test_idx,], label=label[-test_idx],
params=list(eta=.1, subsample=.63, lambda=1000),
objective='binary:logistic', nrounds=250, verbose=0)
pred_penalty <- predict(xgb_penalty, predictors[test_idx,])
error_penalty <- abs(label[test_idx] - pred_penalty) > 0.5
xgb_penalty$evaluation_log[250,]
mean(error_penalty)
1
2
3
4
-
iter train_error
1: 250 0.30966
[1] 0.3286

在 scikit-learn API 中，参数被称为 reg_alpha 和 reg_lambda：

1
2
3
4
5
6
7
xgb_penalty = XGBClassifier(objective='binary:logistic', n_estimators=250,
max_depth=6, reg_lambda=1000, learning_rate=0.1,
subsample=0.63)
xgb_penalty.fit(train_X, train_y)
pred_penalty = xgb_penalty.predict_proba(valid_X)[:, 1]
error_penalty = abs(valid_y - pred_penalty) > 0.5
print('penalty: ', np.mean(error_penalty))

现在，训练误差仅略低于测试集上的误差。

在 R 中，predict 方法提供了一个方便的参数 ntreelimit，它强制仅使用前 \(i\) 棵树进行预测。这使我们能够随着模型的增加，直接比较样本内（in-sample）和样本外（out-of-sample）的错误率：

1
2
3
4
5
6
7
8
error_default <- rep(0, 250)
error_penalty <- rep(0, 250)
for(i in 1:250){
pred_def <- predict(xgb_default, predictors[test_idx,], ntreelimit=i)
error_default[i] <- mean(abs(label[test_idx] - pred_def) >= 0.5)
pred_pen <- predict(xgb_penalty, predictors[test_idx,], ntreelimit=i)
error_penalty[i] <- mean(abs(label[test_idx] - pred_pen) >= 0.5)
}

在 Python 中，我们可以用 ntree_limit 参数调用 predict_proba 方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
results = []
for i in range(1, 250):
train_default = xgb_default.predict_proba(train_X, ntree_limit=i)[:, 1]
train_penalty = xgb_penalty.predict_proba(train_X, ntree_limit=i)[:, 1]
pred_default = xgb_default.predict_proba(valid_X, ntree_limit=i)[:, 1]
pred_penalty = xgb_penalty.predict_proba(valid_X, ntree_limit=i)[:, 1]
results.append({
'iterations': i,
'default train': np.mean(abs(train_y - train_default) > 0.5),
'penalty train': np.mean(abs(train_y - train_penalty) > 0.5),
'default test': np.mean(abs(valid_y - pred_default) > 0.5),
'penalty test': np.mean(abs(valid_y - pred_penalty) > 0.5),
})
results = pd.DataFrame(results)
results.head()

模型的输出将训练集的误差返回到 xgb_default$evaluation_log 组件中。通过将其与样本外误差结合，我们可以绘制误差与迭代次数的关系图：

1
2
3
4
5
6
7
8
errors <- rbind(xgb_default$evaluation_log,
xgb_penalty$evaluation_log,
ata.frame(iter=1:250, train_error=error_default),
data.frame(iter=1:250, train_error=error_penalty))
errors$type <- rep(c('default train', 'penalty train',
'default test', 'penalty test'), rep(250, 4))
ggplot(errors, aes(x=iter, y=train_error, group=type)) +
geom_line(aes(linetype=type, color=type))

我们可以使用 pandas 的 plot 方法创建折线图。从第一个图返回的坐标轴允许我们在同一个图上叠加额外的线条。这是许多 Python 图形包支持的模式：

1
2
3
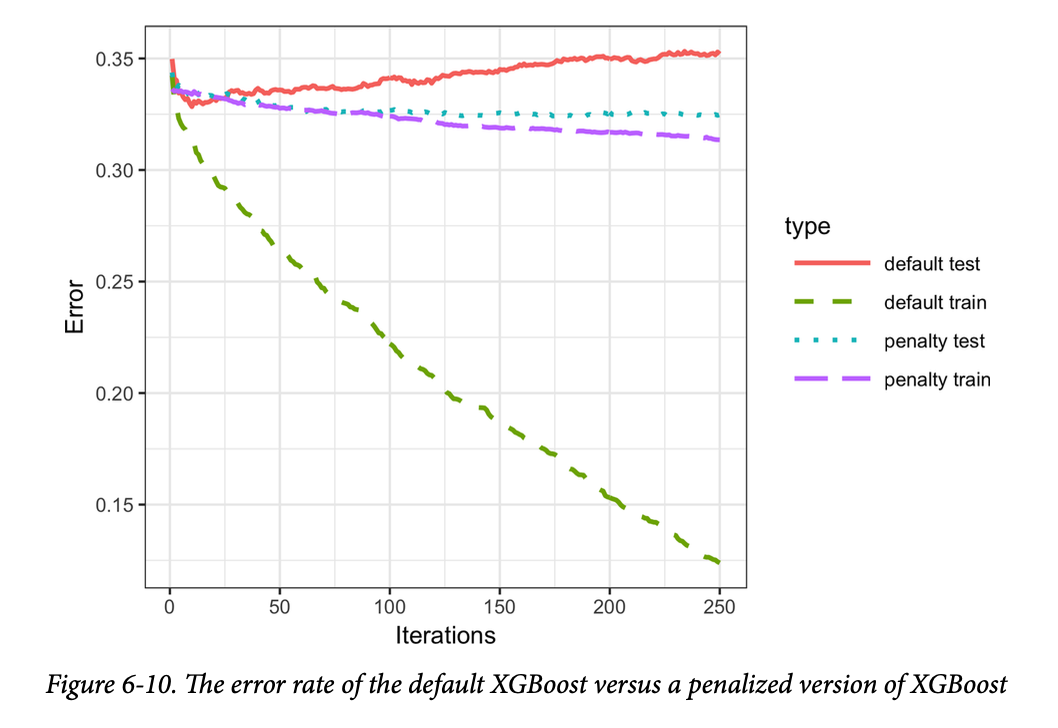
4
ax = results.plot(x='iterations', y='default test')
results.plot(x='iterations', y='penalty test', ax=ax)
results.plot(x='iterations', y='default train', ax=ax)
results.plot(x='iterations', y='penalty train', ax=ax)

结果如图6-10所示。 这表明默认模型在训练集上的准确率稳步提高，但在测试集上的表现实际上却变差了。而正则化后的模型没有表现出这种行为。

F6.10

岭回归和Lasso

通过对模型的复杂度施加惩罚来帮助避免过拟合的技术可以追溯到20世纪70年代。最小二乘回归最小化残差平方和（RSS）；参见第148页的“最小二乘”。岭回归（Ridge regression）最小化残差平方和加上一个惩罚项，该惩罚项是系数数量和大小的函数：

\[ \sum_{i=1}^{n} (Y_i - b_0 - b_1X_1 - \dots - b_pX_p)^2 + \lambda \sum_{j=1}^{p} b_j^2 \] \(\lambda\) 的值决定了对系数的惩罚程度；值越大，产生的模型就越不容易过拟合数据。Lasso 与此类似，不同之处在于它使用曼哈顿距离而不是欧几里得距离作为惩罚项：

\[ \sum_{i=1}^{n} (Y_i - b_0 - b_1X_1 - \dots - b_pX_p)^2 + \alpha \sum_{j=1}^{p} |b_j| \] 使用欧几里得距离也称为 L2 正则化，使用曼哈顿距离则称为 L1 正则化。xgboost 的参数 lambda (reg_lambda) 和 alpha (reg_alpha) 的作用与此类似。

超参数和交叉验证

Hyperparameters and Cross-Validation

xgboost 具有一系列令人望而生畏的超参数；关于讨论，请参见第281页的“XGBoost超参数”。正如在第274页的“正则化：避免过拟合”中所看到的，具体的选择可以显著改变模型拟合。面对如此多的超参数组合可供选择，我们应该如何做出指导性选择呢？解决这个问题的标准方案是使用交叉验证；参见第155页的“交叉验证”。

交叉验证将数据随机分成 \(K\) 个不同的组，也称为折叠（folds）。对于每个折叠，模型在不包含该折叠数据的其余数据上进行训练，然后在该折叠的数据上进行评估。这能得到一个模型在样本外数据上的准确率度量。最佳的超参数集由通过对每个折叠的误差取平均计算出的总体误差最低的模型所决定。

为了说明这项技术，我们将其应用于 xgboost 的参数选择。在这个例子中，我们探讨了两个参数：收缩参数 eta (learning_rate)（参见第272页的“XGBoost”）和树的最大深度 max_depth。参数 max_depth 是从叶子节点到树根的最大深度，默认值为6。这给了我们另一种控制过拟合的方法：深层树往往更复杂，可能导致数据过拟合。

首先，我们设置折叠和参数列表。在 R 中，操作如下：

1
2
3
4
N <- nrow(loan_data)
fold_number <- sample(1:5, N, replace=TRUE)
params <- data.frame(eta = rep(c(.1, .5, .9), 3),
max_depth = rep(c(3, 6, 12), rep(3,3)))

现在，我们使用五个折叠，应用前面描述的算法来计算每个模型和每个折叠的误差：

1
2
3
4
5
6
7
8
9
10
11
12
13
error <- matrix(0, nrow=9, ncol=5)
for(i in 1:nrow(params)){
for(k in 1:5){
fold_idx <- (1:N)[fold_number == k]
xgb <- xgboost(data=predictors[-fold_idx,], label=label[-fold_idx],
params=list(eta=params[i, 'eta'],
max_depth=params[i, 'max_depth']),
objective='binary:logistic', nrounds=100, verbose=0)
pred <- predict(xgb, predictors[fold_idx,])
error[i, k] <- mean(abs(label[fold_idx] - pred) >= 0.5)

}
}

在下面的 Python 代码中，我们创建了所有可能的超参数组合，并使用每种组合来拟合和评估模型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
idx = np.random.choice(range(5), size=len(X), replace=True)
error = []
for eta, max_depth in product([0.1, 0.5, 0.9], [3, 6, 9]):
xgb = XGBClassifier(objective='binary:logistic', n_estimators=250,
max_depth=max_depth, learning_rate=eta)
cv_error = []
for k in range(5):
fold_idx = idx == k
train_X = X.loc[~fold_idx]; train_y = y[~fold_idx]
valid_X = X.loc[fold_idx]; valid_y = y[fold_idx]
xgb.fit(train_X, train_y)
pred = xgb.predict_proba(valid_X)[:, 1]
cv_error.append(np.mean(abs(valid_y - pred) > 0.5))
error.append({
'eta': eta,
'max_depth': max_depth,
'avg_error': np.mean(cv_error)
})
print(error[-1])
errors = pd.DataFrame(error)

我们使用 Python 标准库中的 itertools.product 函数来创建这两个超参数的所有可能组合。

由于我们总共要拟合45个模型，这可能需要一些时间。误差以矩阵形式存储，行代表模型，列代表折叠。使用 rowMeans 函数，我们可以比较不同参数集的误差率：

1
2
avg_error <- 100 * round(rowMeans(error), 4)
cbind(params, avg_error)
1
2
3
4
5
6
7
8
9
10
eta max_depth avg_error
1 0.1 3 32.90
2 0.5 3 33.43
3 0.9 3 34.36
4 0.1 6 33.08
5 0.5 6 35.60
6 0.9 6 37.82
7 0.1 12 34.56
8 0.5 12 36.83
9 0.9 12 38.18

交叉验证表明，使用较浅的树和较小的 eta/learning_rate 值可以得到更准确的结果。由于这些模型也更稳定，因此最佳参数是 eta=0.1 和 max_depth=3（或者可能是 max_depth=6）。

XGBoost 超参数

xgboost 的超参数主要用于在准确率、计算复杂度与过拟合之间取得平衡。有关参数的完整讨论，请参阅 xgboost 文档。

  • eta/learning_rate 应用于提升算法中 \(\alpha\) 的收缩因子，取值范围在0到1之间。默认值为0.3，但对于噪声数据，建议使用较小的值（例如0.1）。在 Python 中，默认值为0.1。

  • nrounds/n_estimators 提升轮数。如果 eta 被设置为一个较小的值，增加轮数很重要，因为算法学习得更慢了。只要包含了一些参数来防止过拟合，更多的轮次并不会带来坏处。

  • max_depth 树的最大深度（默认值为6）。与拟合非常深的树的随机森林相反，提升法通常拟合较浅的树。这有一个好处，即可以避免因噪声数据而在模型中产生虚假复杂的交互作用。在 Python 中，默认值为3。

  • subsample 和 colsample_bytree 无放回抽样的记录比例和用于拟合树的预测变量抽样比例。这些参数类似于随机森林中的参数，有助于避免过拟合。默认值为1.0。

  • lambda/reg_lambda 和 alpha/reg_alpha 用于帮助控制过拟合的正则化参数（参见第274页的“正则化：避免过拟合”）。Python 的默认值为 reg_lambda=1 和 reg_alpha=0。在 R 中，这两个值的默认值均为0。

关键思想

  • 提升法是一类集成模型，它基于拟合一系列模型，并在连续轮次中对具有较大误差的记录赋予更多的权重。
  • 随机梯度提升是最通用的提升类型，并提供最佳性能。最常见的随机梯度提升形式使用树模型。
  • XGBoost 是一种流行且计算高效的随机梯度提升软件包；它可用于数据科学中所有常用语言。
  • 提升法容易过拟合数据，因此需要调优超参数以避免这种情况。
  • 正则化是一种避免过拟合的方法，它通过在模型的参数数量（例如，树的大小）上包含一个惩罚项来实现。
  • 由于需要设置大量的超参数，交叉验证对于提升法尤其重要。

小结

本章描述了两种分类和预测方法，它们灵活且局部地从数据中“学习”，而不是像线性回归那样，从一个对整个数据集进行拟合的结构化模型开始。K-近邻是一种简单的过程，它通过查看周围相似的记录，并将它们的多数类别（或平均值）分配给被预测的记录。树模型则通过尝试各种预测变量的截止（分割）值，迭代地将数据划分为越来越同质的区域和子区域。最有效的分割值形成一条路径，也形成一条通往分类或预测的“规则”。树模型是一种非常强大且流行的预测工具，通常优于其他方法。它们催生了各种集成方法（随机森林、提升法、装袋法），这些方法增强了树的预测能力。