第5章 分类

发表于 分类于

个人注：以下使用gemini翻译 20250916

《Practical Statistics for Data Scientists》书籍英文版
《面向数据科学家的实用统计学》中文版书籍

第5章 分类

数据科学家经常需要为商业问题提供自动化决策。一封电子邮件是钓鱼邮件吗？一个客户是否可能流失？一个网络用户是否可能点击广告？这些都是分类问题，一种监督学习形式。我们首先在已知结果的数据上训练一个模型，然后将该模型应用于结果未知的数据。分类也许是预测最重要的形式：其目标是预测一条记录是1还是0（例如，钓鱼/非钓鱼、点击/不点击、流失/不流失），或者在某些情况下，预测它属于几个类别中的一个（例如，Gmail 将你的收件箱过滤为“主要”、“社交”、“推广”或“论坛”）。

很多时候，我们需要的不仅仅是一个简单的二元分类，我们还想知道一个案例属于某个类别的预测概率。大多数算法都可以返回一个属于目标类别的概率分数（probability score）（倾向性）（propensity），而不仅仅是简单地分配一个二元分类。事实上，对于逻辑回归，R 的默认输出是对数几率（log-odds）尺度，这必须被转换为倾向性。在 Python 的 scikit-learn 中，逻辑回归与大多数分类方法一样，提供了两种预测方法：predict（返回类别）和 predict_proba（返回每个类别的概率）。然后，可以使用一个滑动截止点（ sliding cutoff）将倾向性分数转换为决策。一般方法如下：

  1. 设定一个截止概率：为目标类别设定一个截止概率，如果记录的概率高于这个截止点，我们就认为它属于该类别。
  2. 估算概率：使用任何模型估算一条记录属于目标类别的概率。
  3. 做出决策：如果这个概率高于截止概率，则将新记录分配给目标类别。

截止点越高，被预测为1的记录就越少；截止点越低，被预测为1的记录就越多。

本章将介绍几种用于分类和估算倾向性的关键技术；下一章将描述既可用于分类也可用于数值预测的其他方法。

多于两个类别的情况：

绝大多数问题涉及二元响应。然而，一些分类问题涉及的响应变量可能有多个可能的结果。例如，在客户订阅合同的周年纪念日，可能会有三种结果：客户流失（Y=2）、转为按月合同（Y=1），或签订新的长期合同（Y=0）。目标是预测 \(j=0, 1, 2\) 中的 \(Y=j\)。本章中的大多数分类方法都可以直接或经过简单调整后应用于具有多于两个结果的响应变量。

即使在结果多于两个的情况下，问题通常也可以通过使用条件概率重新定义为一系列二元问题。例如，为了预测合同结果，你可以解决两个二元预测问题：

  • 预测 \(Y=0\) 还是 \(Y>0\)。
  • 在给定 \(Y>0\) 的条件下，预测 \(Y=1\) 还是 \(Y=2\)。

在这种情况下，将问题分解为两个案例是有意义的：（1）客户是否流失；（2）如果他们不流失，他们会选择哪种类型的合同。从模型拟合的角度来看，将多类别问题转换为一系列二元问题通常是有利的，当某个类别比其他类别常见得多时，这种方法尤其有效。

朴素贝叶斯

Naive Bayes

朴素贝叶斯算法利用在给定结果下观察到预测变量的概率，来估计我们真正感兴趣的：在给定一组预测变量值下，观察到结果 \(Y=i\) 的概率。

朴素贝叶斯的关键术语

  • 条件概率（Conditional probability） 在给定某个其他事件（例如，\(Y=i\)）的情况下，观察到某个事件（例如，\(X=i\)）的概率，写作 \(P(X_i | Y_i)\)。

  • 后验概率（Posterior probability） 在结合了预测变量信息之后，某个结果出现的概率（与不考虑预测变量信息的先验概率（prior probability）相反）。

为了理解朴素贝叶斯分类，我们可以从想象完整或精确的贝叶斯分类开始。对于每一条要分类的记录：

  1. 找到所有具有相同预测变量配置文件（即，预测变量值完全相同）的其他记录。
  2. 确定这些记录属于哪些类别，并找出最普遍（即概率最高）的类别。
  3. 将该类别分配给新记录。

上述方法相当于在样本中找到所有与待分类的新记录完全相似的记录，其所有预测变量值都相同。

通用注解：

在标准的朴素贝叶斯算法中，预测变量必须是分类（因子）变量。对于如何使用连续变量，请参阅第200页的“数值预测变量”中的两种变通方法。

为什么精确贝叶斯分类不切实际

Why Exact Bayesian Classification Is Impractical

当预测变量的数量超过少数几个时，许多待分类的记录将找不到精确匹配。考虑一个基于人口统计变量来预测投票的模型。即使是一个相当大的样本，也可能找不到一个完全匹配的新记录，例如：一个来自美国中西部的、高收入的、男性、西班牙裔，在上次选举中投了票，但在上上次选举中没有投票，有三个女儿和一个儿子，并且离了婚。这还只有八个变量，对于大多数分类问题来说，这数量非常小。如果只增加一个有五个同样频繁的类别的新变量，匹配的概率就会降低五倍。

朴素解法

The Naive Solution

在朴素贝叶斯解法中，我们不再将概率计算局限于与待分类记录完全匹配的记录。相反，我们使用整个数据集。朴素贝叶斯算法的步骤如下：

  1. 对于一个二元响应 \(Y=i\)（\(i=0\) 或 \(1\)），估计每个预测变量的个体条件概率 \(P(X_j | Y=i)\)；这些是在观察到 \(Y=i\) 时，预测变量值出现在记录中的概率。该概率通过训练集中属于 \(Y=i\) 记录的 \(X_j\) 值的比例来估计。

  2. 将这些概率相乘，然后乘以属于 \(Y=i\) 的记录比例。

  3. 为所有类别重复步骤1和2。

  4. 通过将步骤2为类别 \(i\) 计算出的值除以所有类别此类值的总和，来估计类别 \(i\) 的概率。

  5. 将该记录分配给在此组预测变量值下具有最高概率的类别。

这个朴素贝叶斯算法也可以用方程来表示，用于计算在给定一组预测变量 \(X_1, \dots, X_p\) 时，观察到结果 \(Y=i\) 的概率：

\[ P(Y=i | X_1, X_2, \dots, X_p) \] 以下是使用精确贝叶斯分类计算类别概率的完整公式：

\[ P(Y=i | X_1, X_2, \dots, X_p) = \frac{P(Y=i)P(X_1, \dots, X_p | Y=i)}{P(Y=0)P(X_1, \dots, X_p | Y=0) + P(Y=1)P(X_1, \dots, X_p | Y=1)} \]

在朴素贝叶斯条件独立性的假设下，这个方程变为：

\[ P(Y=i | X_1, X_2, \dots, X_p) = \frac{P(Y=i)P(X_1 | Y=i) \dots P(X_p | Y=i)}{P(Y=0)P(X_1 | Y=0) \dots P(X_p | Y=0) + P(Y=1)P(X_1 | Y=1) \dots P(X_p | Y=1)} \]

为什么这个公式被称为“朴素”？我们做了一个简化的假设：在观察到某个结果时，预测变量向量的精确条件概率，可以由个体条件概率的乘积来很好地估计。换句话说，在估计 \(P(X_j | Y=i)\) 而不是 \(P(X_1, X_2, \dots, X_p | Y=i)\) 时，我们假设 \(X_j\) 独立于所有其他预测变量 \(X_k\)（\(k \neq j\)）。

在 R 语言中，可以使用几个包来估计朴素贝叶斯模型。以下代码使用 klaR 包对贷款支付数据进行模型拟合：

1
2
3
4
library(klaR)
naive_model <- NaiveBayes(outcome ~ purpose_ + home_ + emp_len_,
data = na.omit(loan_data))
naive_model$table

模型的输出是条件概率 \(P(X_j | Y=i)\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
$purpose_
var
grouping credit_card debt_consolidation home_improvement major_purchase
paid off 0.18759649 0.55215915 0.07150104 0.05359270
default 0.15151515 0.57571347 0.05981209 0.03727229
var
grouping medical other small_business
paid off 0.01424728 0.09990737 0.02099599
default 0.01433549 0.11561025 0.04574126
$home_
var
grouping MORTGAGE OWN RENT
paid off 0.4894800 0.0808963 0.4296237
default 0.4313440 0.0832782 0.4853778
$emp_len_
var
grouping < 1 Year > 1 Year
paid off 0.03105289 0.96894711
default 0.04728508 0.95271492

在 Python 中，我们可以使用 scikit-learn 中的 sklearn.naive_bayes.MultinomialNB。在拟合模型之前，我们需要将分类特征转换为虚拟变量：

1
2
3
4
5
6
7
8
predictors = ['purpose_', 'home_', 'emp_len_']
outcome = 'outcome'
X = pd.get_dummies(loan_data[predictors], prefix=
y = loan_data[outcome]
''
'')
naive_model = MultinomialNB(alpha=0.01, fit_prior=True)
naive_model.fit(X, y)

可以通过 feature_log_prob_ 属性从拟合模型中获得条件概率。

该模型可用于预测一笔新贷款的结果。我们使用数据集的最后一条记录进行测试：

1
2
3
new_loan <- loan_data[147, c('purpose_', 'home_', 'emp_len_')]
row.names(new_loan) <- NULL
new_loan
1
2
purpose_ home_ emp_len_
1 small_business MORTGAGE > 1 Year

在 Python 中，我们按如下方式获取此值：

1
new_loan = X.loc[146:146, :]

在这种情况下，模型预测为违约（R）：

1
predict(naive_model, new_loan)
1
2
3
4
5
6
$class
[1] default
Levels: paid off default
$posterior
paid off default
[1,] 0.3463013 0.6536987

正如我们所讨论的，scikit-learn 的分类模型有两个方法：predict，返回预测的类别；以及 predict_proba，返回类别概率：

1
2
3
4
print('predicted class: ', naive_model.predict(new_loan)[0])
probabilities = pd.DataFrame(naive_model.predict_proba(new_loan),
columns=loan_data[outcome].cat.categories)
print('predicted probabilities', probabilities)
1
2
3
4
predicted class: default
predicted probabilities
   default  paid off
0  0.653696  0.346304

预测还返回了违约概率的后验估计。众所周知，朴素贝叶斯分类器会产生有偏的估计（biased estimates.）。然而，当目标是根据 \(Y=1\) 的概率对记录进行排序时，不需要无偏的概率估计，并且朴素贝叶斯会产生良好的结果。

数值预测变量

Numeric Predictor Variables

贝叶斯分类器只适用于分类（因子）预测变量，例如在垃圾邮件分类中，预测任务的核心在于单词、短语、字符等的出现与否。如果想将朴素贝叶斯应用于数值预测变量，必须采取以下两种方法之一：

  • 分箱和转换：将数值预测变量分箱并转换为分类预测变量，然后应用上一节介绍的算法。
  • 使用概率模型：例如，使用正态分布（参见第69页的“正态分布”）来估计条件概率 \(P(X_j | Y=i)\)。

警告：

当训练数据中某个预测变量类别不存在时，算法会将新数据中相应结果变量的概率赋值为零，而不是像其他方法那样简单地忽略此变量并利用其他变量的信息。大多数朴素贝叶斯的实现都使用一个平滑参数（拉普拉斯平滑）来防止这种情况发生。

关键思想

  • 适用范围：朴素贝叶斯适用于分类（因子）预测变量和结果。
  • 核心问题：它会问，“在每个结果类别中，哪个预测变量类别最有可能出现？”
  • 反向推断：然后，该信息被反向用于估计在给定预测变量值的情况下，结果类别的概率。

判别分析

Discriminant Analysis

判别分析是最早出现的统计分类器，由R. A. Fisher于1936年在《优生学年鉴》杂志上发表的一篇文章中提出。

判别分析的关键术语

  • 协方差 (Covariance) 衡量一个变量与另一个变量共同变化的程度（即，相似的大小和方向）。

  • 判别函数 (Discriminant function) 应用于预测变量时，能最大化类别间分离度的函数。

  • 判别权重 (Discriminant weights) 应用判别函数后得到的分数，用于估计记录属于某个类别的概率。

尽管判别分析涵盖了多种技术，但最常用的是线性判别分析（Linear Discriminant Analysis, LDA）。Fisher最初提出的方法与今天的LDA略有不同，但其机制基本相同。随着树模型和逻辑回归等更复杂技术的出现，LDA的应用现在已不如从前广泛。

然而，在某些应用中你仍然可能遇到LDA，而且它与其他更广泛使用的方法（如主成分分析；参见第284页的“主成分分析”）存在联系。

警告：

线性判别分析（LDA）不应与潜在狄利克雷分配（Latent Dirichlet Allocation, LDA）混淆。后者用于文本和自然语言处理，与线性判别分析无关。

协方差矩阵

Covariance Matrix

要理解判别分析，首先有必要引入两个或多个变量之间的协方差概念。协方差衡量了两个变量 x 和 z 之间的关系。用 \(\bar{x}\) 和 \(\bar{z}\) 表示每个变量的均值（参见第9页的“均值”）。\(x\) 和 \(z\) 之间的协方差 \(s_{x, z}\) 由以下公式给出：

\[ s_{x, z} = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(z_i - \bar{z})}{n - 1} \]

其中，\(n\) 是记录的数量（注意我们用 \(n-1\) 而不是 \(n\) 来除；参见第15页的“自由度，以及 \(n\) 还是 \(n-1\)？”）。

与相关系数（参见第30页的“相关性”）一样，正值表示正向关系，负值表示负向关系。然而，相关系数被限制在-1和1之间，而协方差的尺度取决于变量 \(x\) 和 \(z\) 的尺度。由 \(x\) 和 \(z\) 组成的协方差矩阵 \(\Sigma\) 的对角线上（行和列是同一变量）是各个变量的方差 \(s_x^2\) 和 \(s_z^2\)，非对角线上是变量对之间的协方差：

\[ \Sigma = \begin{pmatrix} s_x^2 & s_{x,z} \\ s_{z,x} & s_z^2 \end{pmatrix} \]

通用注解：

回想一下，标准差用于将一个变量标准化为z分数；协方差矩阵则用于这种标准化过程的多元扩展。这被称为马哈拉诺比斯距离（Mahalanobis distance）（参见第242页的“其他距离度量”），并与 LDA 函数相关。

费舍尔线性判别

Fisher’s Linear Discriminant

为了简化，我们关注一个分类问题：使用两个连续数值变量 \(x\) 和 \(z\) 来预测一个二元结果 \(y\)。从技术上讲，判别分析假定预测变量是正态分布的连续变量，但实际上，即使在非极端的非正态性或二元预测变量情况下，该方法也表现良好。费舍尔线性判别将组间变异与组内变异区分开来。具体来说，为了将记录分为两组，线性判别分析（LDA）侧重于最大化“组间”平方和 \(SS_{between}\)（衡量两组之间的变异）相对于“组内”平方和 \(SS_{within}\)（衡量组内变异）的比率。在这里，这两组对应于 \(y=0\) 的记录（\(x_0, z_0\)）和 \(y=1\) 的记录（\(x_1, z_1\)）。

该方法找到能够最大化平方和比率的线性组合 \(w_x x + w_z z\)：

\[ \frac{SS_{between}}{SS_{within}} \]

组间平方和是两个组均值之间的平方距离，而组内平方和是每组内部围绕均值的扩散程度，并由协方差矩阵加权。直观地，通过最大化组间平方和并最小化组内平方和，该方法实现了两组之间最大的分离度。

一个简单的例子

与书籍《Modern Applied Statistics with S》（作者：W. N. Venables 和 B. D. Ripley，1994年，Springer出版社）相关的 MASS 包提供了在 R 中进行 LDA 的函数。以下代码将该函数应用于一个贷款样本数据，使用了两个预测变量 borrower_score 和 payment_inc_ratio，并打印出估计的线性判别权重：

1
2
3
4
library(MASS)
loan_lda <- lda(outcome ~ borrower_score + payment_inc_ratio,
data=loan3000)
loan_lda$scaling
1
2
3
LD1
borrower_score     7.17583880
payment_inc_ratio -0.09967559

在 Python 中，我们可以使用 sklearn.discriminant_analysis 中的 LinearDiscriminantAnalysis。scalings_ 属性给出了估计的权重：

1
2
3
4
5
6
7
8
loan3000.outcome = loan3000.outcome.astype('category')
predictors = ['borrower_score', 'payment_inc_ratio']
outcome = 'outcome'
X = loan3000[predictors]
y = loan3000[outcome]
loan_lda = LinearDiscriminantAnalysis()
loan_lda.fit(X, y)
pd.DataFrame(loan_lda.scalings_, index=X.columns)

通用注解：

使用判别分析进行特征选择：如果在运行 LDA 之前对预测变量进行标准化，那么判别权重可以作为变量重要性的度量，从而提供一种计算高效的特征选择方法。

lda 函数可以预测“违约”与“已还清”的概率：

1
2
pred <- predict(loan_lda)
head(pred$posterior)
1
2
3
4
5
6
7
paid off  default
1 0.4464563 0.5535437
2 0.4410466 0.5589534
3 0.7273038 0.2726962
4 0.4937462 0.5062538
5 0.3900475 0.6099525
6 0.5892594 0.4107406

拟合模型的 predict_proba 方法返回“违约”和“已还清”结果的概率：

1
2
3
pred = pd.DataFrame(loan_lda.predict_proba(loan3000[predictors]),
columns=loan_lda.classes_)
pred.head()

绘制预测结果的图表有助于说明 LDA 的工作原理。使用 predict 函数的输出，可以按如下方式生成违约概率的估计图：

1
2
3
4
5
6
7
8
9
10
center <- 0.5 * (loan_lda$mean[1, ] + loan_lda$mean[2, ])
slope <- -loan_lda$scaling[1] / loan_lda$scaling[2]
intercept <- center[2] - center[1] * slope
ggplot(data=lda_df, aes(x=borrower_score, y=payment_inc_ratio,
color=prob_default)) +
geom_point(alpha=.6) +
scale_color_gradientn(colors=c('#ca0020', '#f7f7f7', '#0571b0')) +
scale_x_continuous(expand=c(0,0)) +
scale_y_continuous(expand=c(0,0), lim=c(0, 20)) +
geom_abline(slope=slope, intercept=intercept, color='darkgreen')

在 Python 中，使用以下代码创建类似的图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Use scalings and center of means to determine decision boundary
center = np.mean(loan_lda.means_, axis=0)
slope = - loan_lda.scalings_[0] / loan_lda.scalings_[1]
intercept = center[1] - center[0] * slope
# payment_inc_ratio for borrower_score of 0 and 20
x_0 = (0 - intercept) / slope
x_20 = (20 - intercept) / slope
lda_df = pd.concat([loan3000, pred['default']], axis=1)
lda_df.head()
fig, ax = plt.subplots(figsize=(4, 4))
g = sns.scatterplot(x='borrower_score', y='payment_inc_ratio',
hue='default', data=lda_df,
palette=sns.diverging_palette(240, 10, n=9, as_cmap=True),
ax=ax, legend=False)
ax.set_ylim(0, 20)
ax.set_xlim(0.15, 0.8)
ax.plot((x_0, x_20), (0, 20), linewidth=3)
ax.plot(*loan_lda.means_.transpose())

由此产生的图表如图5-1所示。对角线左侧的数据点被预测为违约（概率大于0.5）。

F5.1

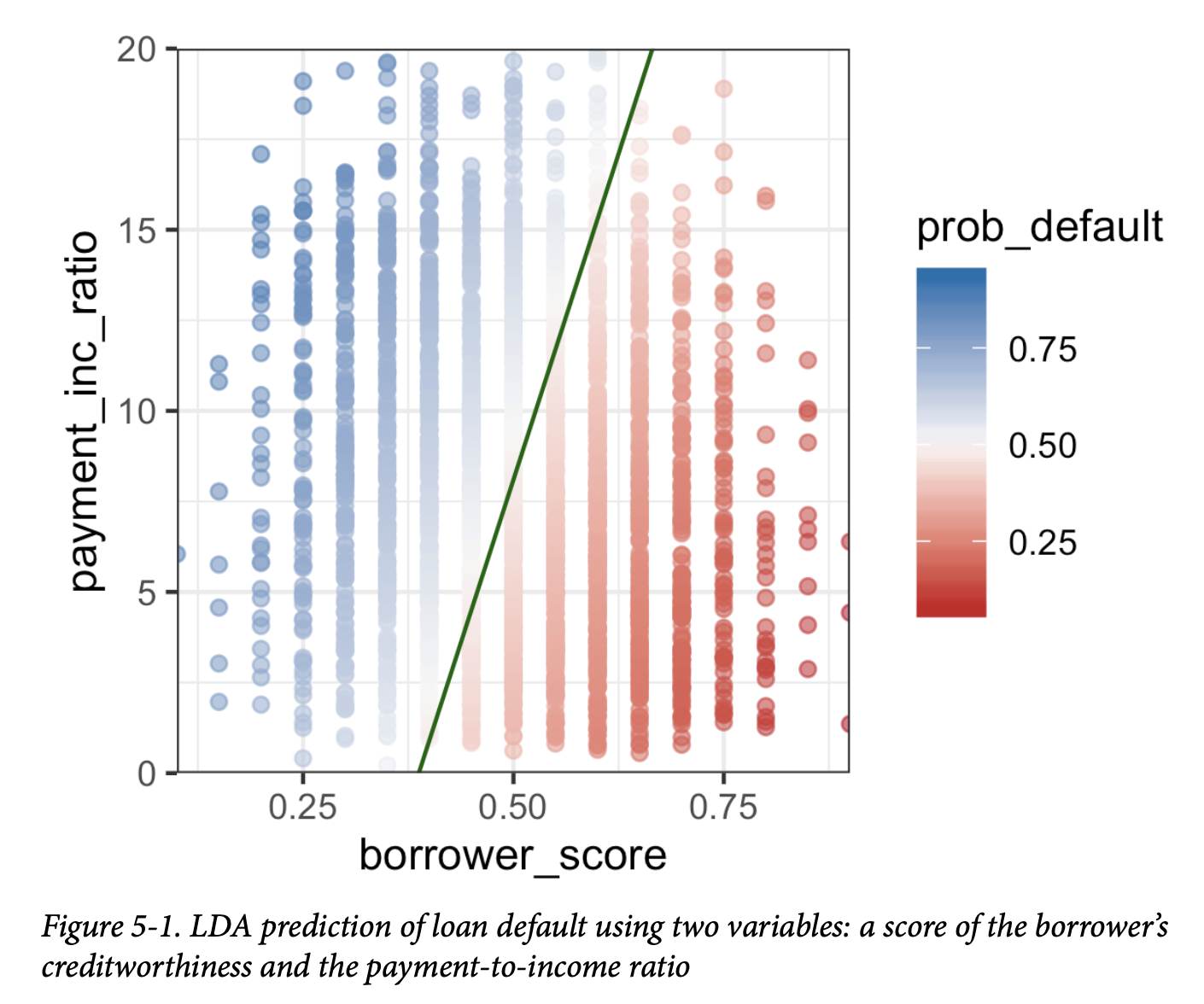
使用判别函数权重，LDA 将预测变量空间分为两个区域，如图中的实线所示。离这条线越远（两个方向上），预测的置信度越高（即，概率越远离0.5）。

通用注解：

判别分析的扩展Extensions of Discriminant Analysis更多预测变量：尽管本节的文字和示例只使用了两个预测变量，但 LDA 对于多于两个预测变量的情况同样有效。唯一的限制因素是记录的数量（估计协方差矩阵需要每个变量有足够的记录，这在数据科学应用中通常不是问题）。

判别分析还有其他变体。其中最著名的是二次判别分析（Quadratic Discriminant Analysis, QDA）。尽管其名称如此，QDA 仍然是一种线性判别函数。主要区别在于，在 LDA 中，我们假定对应于 \(Y=0\) 和 \(Y=1\) 的两组拥有相同的协方差矩阵。而在 QDA 中，允许这两组拥有不同的协方差矩阵。在实践中，这种差异在大多数应用中并不重要。

关键思想

  • 适用范围：判别分析适用于连续或分类预测变量，以及分类结果。
  • 工作原理：它使用协方差矩阵计算一个线性判别函数，该函数用于区分属于一个类别的记录和属于另一个类别的记录。
  • 结果：该函数应用于每条记录，以推导出权重或分数（每个可能的类别一个），从而确定其估计的类别。

逻辑回归

Logistic Regression

逻辑回归与多元线性回归（参见第4章）类似，但其结果是二元的。它采用各种转换方法，将问题转化为一个可以拟合线性模型的形式。与K-最近邻和朴素贝叶斯不同，逻辑回归是一种结构化模型方法（a structured model approach），而非以数据为中心的方法（a data-centric approach）。由于其计算速度快，且输出的模型有助于快速对新数据进行评分，因此它是一种非常流行的方法。

逻辑回归的关键术语

  • Logit（逻辑函数） 将类别成员资格的概率映射到 \(\pm \infty\) 范围（而不是0到1）的函数。 同义词：对数几率（见下文）

  • Odds（几率） “成功”（1）与“不成功”（0）的比率。

  • Log odds（对数几率） 转换后模型中的响应变量（现在是线性的），该值可以被映射回概率。

逻辑响应函数与 Logit

Logistic Response Function and Logit

逻辑回归的关键要素是逻辑响应函数和 logit，通过它们我们将概率（在0-1的尺度上）映射到一个更广的、适合线性建模的尺度。

第一步是将结果变量视为标签为“1”的概率 \(p\)。直观地，我们可能会试图将 \(p\) 建模为预测变量的线性函数：

\[ p = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_qx_q \] 然而，拟合这个模型并不能确保 \(p\) 最终会落在0到1之间，而概率必须如此。

相反，我们通过对预测变量应用逻辑响应或逆 Logit 函数来建模 \(p\)：

\[ p = \frac{1}{1 + e^{-(\beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_qx_q)}} \] 这个转换确保了 \(p\) 始终在0到1之间。

为了摆脱分母中的指数表达式，我们考虑几率（Odds）而非概率。几率是“成功”（1）与“不成功”（0）的比率，这对于任何地方的押注者来说都很熟悉。用概率表示，几率是一个事件发生的概率除以该事件不发生的概率。例如，如果一匹马获胜的概率是0.5，那么“不会获胜”的概率是 (1-0.5)=0.5，几率就是1.0：

\[ \text{Odds}(Y=1) = \frac{p}{1-p} \] 我们可以使用逆几率函数从几率中获得概率：

\[ p = \frac{\text{Odds}}{1 + \text{Odds}} \] 我们将此与前面展示的逻辑响应函数结合起来，得到：

\[ \text{Odds}(Y=1) = e^{\beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_qx_q} \] 最后，对两边取对数，我们得到一个涉及预测变量线性函数的表达式：

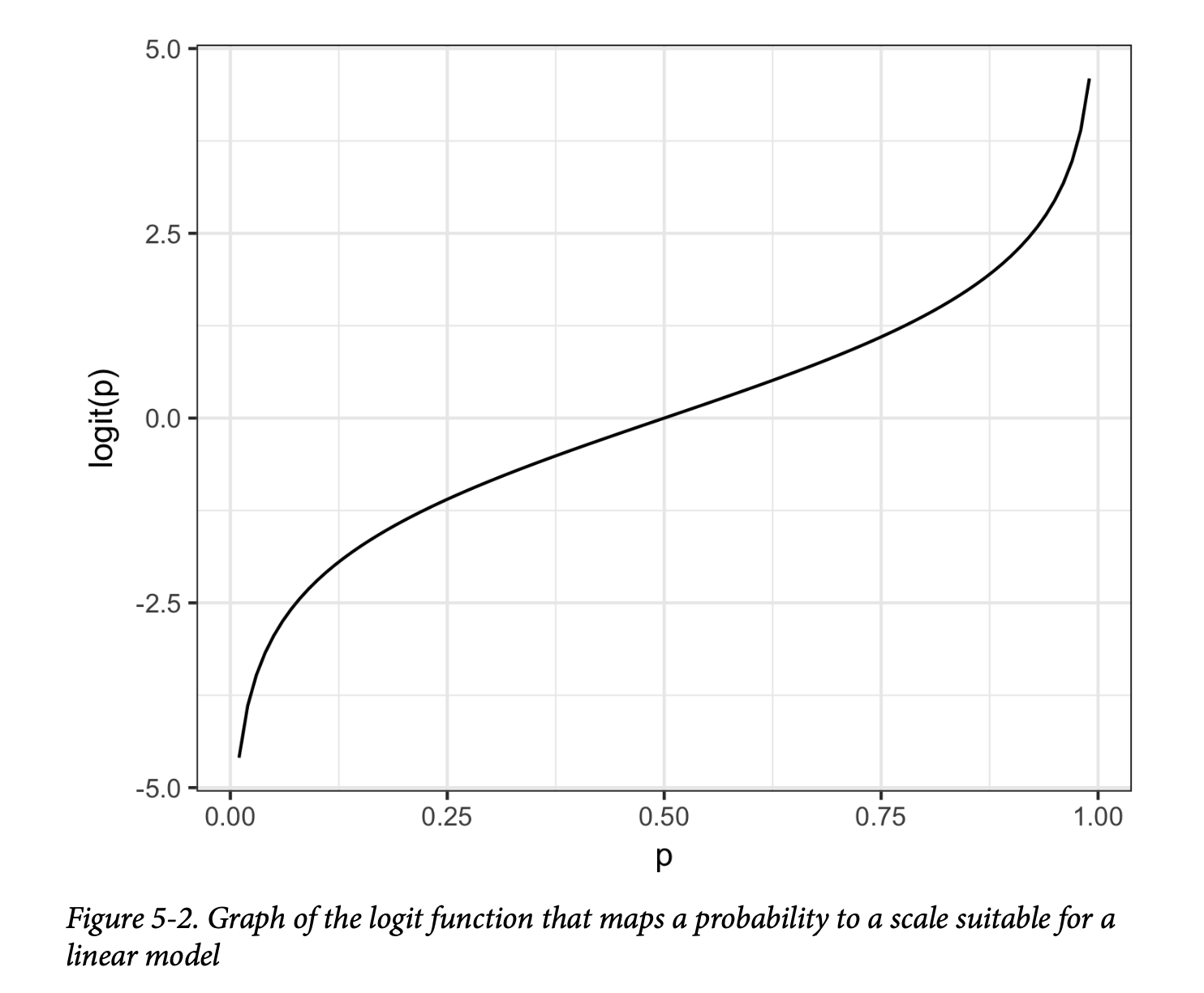
\[ \log(\text{Odds}(Y=1)) = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_qx_q \] 对数几率函数，也称为 logit 函数，将概率 \(p\) 从 [0, 1] 映射到任意值 \([-\infty, +\infty]\)（见图5-2）。转换的循环完成；我们使用一个线性模型来预测一个概率，然后我们可以通过应用一个截止规则，将该概率映射回一个类别标签——任何概率大于截止点的记录都被归类为1。

F5.2

逻辑回归与广义线性模型 (GLM)

Logistic Regression and the GLM

逻辑回归公式中的响应变量是二元结果为1的对数几率。我们只观察到二元结果本身，而不是对数几率，因此需要特殊的统计方法来拟合方程。逻辑回归是广义线性模型（GLM）的一个特例，该模型旨在将线性回归扩展到其他情境。

在 R 中，要拟合逻辑回归，需要使用 glm 函数并将 family 参数设置为 binomial。以下代码使用第238页“K-最近邻”中引入的个人贷款数据来拟合逻辑回归：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
logistic_model <- glm(outcome ~ payment_inc_ratio + purpose_ +
home_ + emp_len_ + borrower_score,
data=loan_data, family='binomial')
logistic_model
Call: glm(formula = outcome ~ payment_inc_ratio + purpose_ + home_ +
emp_len_ + borrower_score, family = "binomial", data = loan_data)

Coefficients:
(Intercept) payment_inc_ratio
1.63809 0.07974
purpose_debt_consolidation purpose_home_improvement
0.24937 0.40774
purpose_major_purchase purpose_medical
0.22963 0.51048
purpose_other purpose_small_business
0.62066 1.21526
home_OWN home_RENT
0.04833 0.15732
emp_len_ > 1 Year borrower_score
-0.35673 -4.61264
Degrees of Freedom: 45341 Total (i.e. Null); 45330 Residual
Null Deviance: 62860
Residual Deviance: 57510 AIC: 57540

响应变量是 outcome，如果贷款已还清则为0，如果违约则为1。purpose_ 和 home_ 是因子变量，分别代表贷款目的和房屋所有权状态。与线性回归一样，一个有 P 个水平的因子变量用 P-1 列来表示。在 R 中，默认使用参考编码，所有水平都与参考水平进行比较（参见第163页的“回归中的因子变量”）。这些因子的参考水平分别是 credit_card 和 MORTGAGE。borrower_score 变量是一个从0到1的分数，代表借款人的信用度（从差到优秀）。这个变量是使用K-最近邻从其他几个变量创建的——参见第247页的“KNN 作为特征工程”。

在 Python 中，我们使用 sklearn.linear_model 中的 LogisticRegression 类。penalty 和 C 参数用于通过 L1 或 L2 正则化防止过拟合。正则化默认是开启的。为了在不进行正则化的情况下拟合，我们将 C 设置为一个非常大的值。solver 参数选择使用的优化器；liblinear 方法是默认的：

1
2
3
4
5
6
7
8
9
10
11
12
predictors = ['payment_inc_ratio', 'purpose_', 'home_', 'emp_len_',
'borrower_score']
outcome = 'outcome'
X = pd.get_dummies(loan_data[predictors], prefix=
''
, prefix_sep=
''
,
drop_first=True)
y = loan_data[outcome]
logit_reg = LogisticRegression(penalty='l2', C=1e42, solver='liblinear')
logit_reg.fit(X, y)

与 R 不同，scikit-learn 从 y 中的唯一值（paid off 和 default）派生出类别。在内部，这些类别按字母顺序排序。由于这与 R 中使用的因子顺序相反，你会发现系数是相反的。predict 方法返回类别标签，而 predict_proba 返回从 logit_reg.classes_ 属性中可用的顺序的概率。

广义线性模型

Generalized Linear Models

广义线性模型（Generalized Linear Models, GLMs）由两个主要部分构成：

  • 一个概率分布或族：在逻辑回归中是二项分布。
  • 一个链接函数：将响应变量映射到预测变量的转换函数，在逻辑回归中是 logit。

逻辑回归是迄今为止最常见的 GLM 形式。数据科学家也会遇到其他类型的 GLM。有时会使用 log 链接函数而不是 logit；在实践中，对于大多数应用，使用 log 链接函数不太可能导致非常不同的结果。泊松分布通常用于建模计数数据（例如，一个用户在特定时间内访问网页的次数）。其他族包括负二项分布和伽马分布，它们常用于建模经过的时间（例如，到故障的时间）。与逻辑回归相比，使用这些模型的 GLM 应用更为细致，需要更谨慎。除非你熟悉并理解这些方法的效用和陷阱，否则最好避免使用它们。

逻辑回归的预测值

Predicted Values from Logistic Regression

逻辑回归的预测值是对数几率：\(\hat{Y }= \log(\text{Odds}(Y=1))\)。预测概率由逻辑响应函数给出：

\[ \hat{p} = \frac{1}{1 + e^{- \hat{Y}}} \] 例如，查看 R 中 logistic_model 的预测：

1
2
pred <- predict(logistic_model)
summary(pred)
1
2
Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.704774 -0.518825 -0.008539 0.002564 0.505061 3.509606

在 Python 中，我们可以将概率转换为数据框，并使用 describe 方法来获取分布的这些特征：

1
2
3
pred = pd.DataFrame(logit_reg.predict_log_proba(X),
columns=loan_data[outcome].cat.categories)
pred.describe()

将这些值转换为概率是一个简单的转换：

1
prob <- 1/(1 + exp(-pred))
1
2
3
> summary(prob)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.06269 0.37313 0.49787 0.50000 0.62365 0.97096

scikit-learn 中的 predict_proba 方法可以直接获得概率：

1
2
3
pred = pd.DataFrame(logit_reg.predict_proba(X),
columns=loan_data[outcome].cat.categories)
pred.describe()

这些值在0到1的范围内，但它们尚未声明预测值是违约还是已还清。我们可以将任何大于0.5的值声明为违约。在实践中，如果目标是识别罕见类别的成员，通常采用较低的截止点是合适的（参见第223页的“罕见类别问题”）。

系数与几率比的解释

Interpreting the Coefficients and Odds Ratios

逻辑回归的一个优点是，它产生的模型可以快速地在新数据上进行评分，无需重新计算。另一个优点是，与其他分类方法相比，它相对更容易解释。其核心概念是理解几率比(odds ratio)。对于一个二元因子变量 \(X\) 来说，几率比最容易理解：

\[ \text{几率比} = \frac{\text{Odds}(Y=1 | X=1)}{\text{Odds}(Y=1 | X=0)} \] 这被解释为当 \(X=1\) 时的几率与当 \(X=0\) 时的几率之比。如果几率比是2，那么当 \(X=1\) 时 \(Y=1\) 的几率是当 \(X=0\) 时的两倍。

为什么我们要用几率比而不是概率？我们使用几率是因为，在逻辑回归中，系数 \(\beta_j\) 是 \(X_j\) 几率比的对数。

一个例子可以更清楚地说明这一点。对于第210页“逻辑回归与 GLM”中拟合的模型，purpose_small_business 的回归系数是1.21526。这意味着，与用于偿还信用卡债务的贷款相比，用于创建或扩展小企业的贷款，其违约与已还清的几率比减少了 \(e^{1.21526} \approx 3.4\) 倍。显然，用于创建或扩展小企业的贷款比其他类型的贷款风险高得多。

F5.3

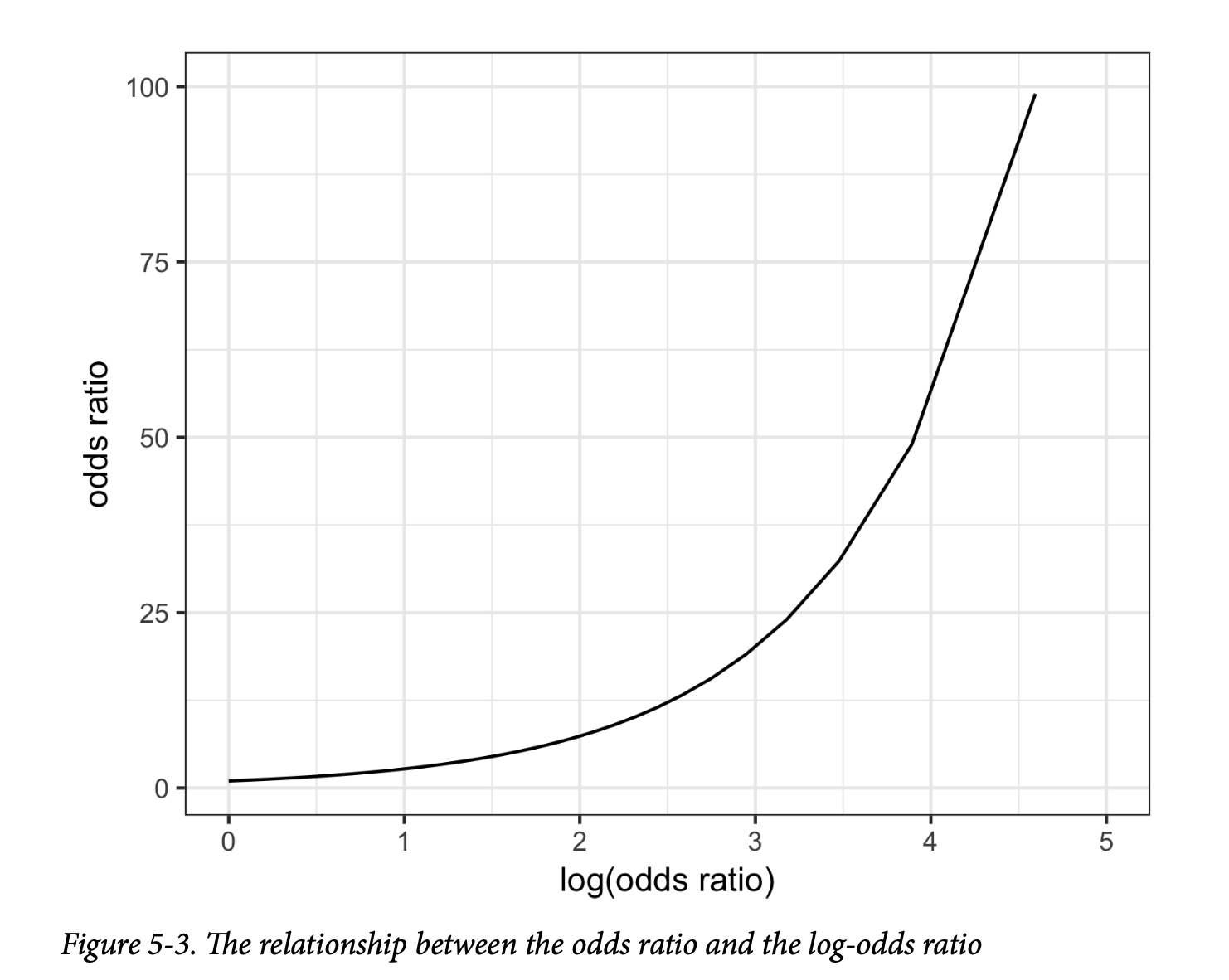
图5-3显示了当几率比大于1时，几率比和对数几率比之间的关系。由于系数在对数尺度上，系数增加1，会导致几率比增加 \(e^1 \approx 2.72\) 倍。

数值变量 \(X\) 的几率比可以类似地解释：它们衡量 \(X\) 变化一个单位时几率比的变化。例如，付款收入比从5增加到6，将使贷款违约的几率增加 \(e^{0.08244} \approx 1.09\) 倍。变量 borrower_score 是衡量借款人信用度的分数，范围从0（低）到1（高）。信用度最好的借款人相对于最差的借款人违约的几率比，要小 \(e^{-4.61264} \approx 0.01\) 倍。换句话说，信用度最差的借款人的违约风险是信用度最好的借款人的100倍！

线性回归与逻辑回归：相似点与差异

Linear and Logistic Regression: Similarities and Differences

线性回归和逻辑回归有许多共同点。两者都假设预测变量与响应变量之间存在参数化的线性形式。探索和寻找最佳模型的方式也十分相似。线性模型的扩展，例如使用样条变换预测变量（参见第189页的“样条回归”），同样适用于逻辑回归。

然而，逻辑回归在两个根本方面有所不同： * 模型的拟合方式（不适用最小二乘法）。 * 模型残差的性质和分析。

模型拟合

线性回归使用最小二乘法进行拟合，其拟合质量通过 RMSE 和 R-squared 统计量进行评估。在逻辑回归中（与线性回归不同），没有闭合形式的解，模型必须使用最大似然估计（MLE）进行拟合。最大似然估计是一个试图找到最有可能产生我们所观察到的数据的模型的过程。在逻辑回归方程中，响应变量不是0或1，而是对响应为1的对数几率的估计。最大似然估计找到的解，使得估计的对数几率能够最好地描述观察到的结果。该算法的机制涉及一种拟牛顿优化，它在基于当前参数的评分步骤（费舍尔评分）和更新参数以改善拟合之间进行迭代。

最大似然估计（MLE）

如果你对统计符号感兴趣，这里有更多细节：假设有一组数据 \(X_1, X_2, \dots, X_n\) 和一个依赖于一组参数 \(\theta\) 的概率模型 \(P_\theta(X_1, X_2, \dots, X_n)\)。MLE 的目标是找到能够最大化 \(P_\theta(X_1, X_2, \dots, X_n)\) 值的参数集 \(\theta\)；也就是说，它最大化在给定模型 \(P\) 的情况下观察到 \(X_1, X_2, \dots, X_n\) 的概率。在拟合过程中，模型使用一个称为偏差（deviance）的度量进行评估：

\[ \text{偏差} = -2 \log P_\theta(X_1, X_2, \dots, X_n) \] 偏差越低 (个人注：因为有负号) ，拟合效果越好。

幸运的是，大多数实践者不需要关注拟合算法的细节，因为这些都由软件自动处理。大多数数据科学家无需担心拟合方法，只需理解它是在特定假设下找到一个好模型的方式即可。

警告：

处理因子变量（Handling Factor Variables）

在逻辑回归中，因子变量应像在线性回归中一样进行编码；参见第163页的“回归中的因子变量”。在 R 和其他软件中，这通常是自动处理的，并且通常使用参考编码。

本章涵盖的所有其他分类方法通常使用独热编码表示（参见第242页的“独热编码”）。在 Python 的 scikit-learn 中，最容易使用独热编码，这意味着在回归中只能使用由此产生的 \(n-1\) 个虚拟变量。

模型评估

Assessing the Model

像其他分类方法一样，逻辑回归模型的评估标准是其对新数据的分类准确性（参见第219页的“评估分类模型”）。与线性回归一样，一些标准的统计工具可用于检查和改进模型。除了估计的系数外，R 还会报告系数的标准误（SE）、z 值和 p 值：

1
summary(logistic_model)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Call:
glm(formula = outcome ~ payment_inc_ratio + purpose_ + home_ +
emp_len_ + borrower_score, family = "binomial", data = loan_data)
Deviance Residuals:
Min       1Q   Median       3Q      Max
-2.51951 -1.06908 -0.05853  1.07421  2.15528
Coefficients:
                           Estimate  Std. Error z value Pr(>|z|)
(Intercept)                 1.638092   0.073708  22.224  < 2e-16 ***
payment_inc_ratio           0.079737   0.002487  32.058  < 2e-16 ***
purpose_debt_consolidation  0.249373   0.027615   9.030  < 2e-16 ***
purpose_home_improvement    0.407743   0.046615   8.747  < 2e-16 ***
purpose_major_purchase      0.229628   0.053683   4.277  1.89e-05 ***
purpose_medical             0.510479   0.086780   5.882  4.04e-09 ***
purpose_other               0.620663   0.039436  15.738  < 2e-16 ***
purpose_small_business      1.215261   0.063320  19.192  < 2e-16 ***
home_OWN                    0.048330   0.038036   1.271  0.204
home_RENT                   0.157320   0.021203   7.420  1.17e-13 ***
emp_len_ > 1 Year           -0.356731   0.052622  -6.779  1.21e-11 ***
borrower_score              -4.612638   0.083558 -55.203  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 62857  on 45341  degrees of freedom
Residual deviance: 57515  on 45330  degrees of freedom
AIC: 57539
Number of Fisher Scoring iterations: 4

statsmodels 包有一个广义线性模型（GLM）的实现，它提供了类似详细的信息：

1
2
3
4
5
y_numbers = [1 if yi == 'default' else 0 for yi in y]
logit_reg_sm = sm.GLM(y_numbers, X.assign(const=1),
family=sm.families.Binomial())
logit_result = logit_reg_sm.fit()
logit_result.summary()

p 值的解释与回归中的情况具有相同的警告，应将其更多地视为变量重要性的相对指标（参见第153页的“评估模型”），而不是作为统计显著性的正式度量。一个具有二元响应的逻辑回归模型没有相关的 RMSE 或 R-squared。相反，逻辑回归模型通常使用更通用的分类指标进行评估；参见第219页的“评估分类模型”。

许多线性回归的概念也适用于逻辑回归（以及其他 GLM）。例如，你可以使用逐步回归、拟合交互项，或包含样条项。关于混杂变量和相关变量的相同问题也适用于逻辑回归（参见第169页的“解释回归方程”）。你可以使用 R 中的 mgcv 包拟合广义加性模型（参见第192页的“广义加性模型”）：

1
2
3
logistic_gam <- gam(outcome ~ s(payment_inc_ratio) + purpose_ +
home_ + emp_len_ + s(borrower_score),
data=loan_data, family='binomial')

statsmodels 的公式接口在 Python 中也支持这些扩展：

1
2
3
4
5
import statsmodels.formula.api as smf
formula = ('outcome ~ bs(payment_inc_ratio, df=4) + purpose_ + ' +
'home_ + emp_len_ + bs(borrower_score, df=4)')
model = smf.glm(formula=formula, data=loan_data, family=sm.families.Binomial())
results = model.fit()

残差分析

Analysis of residuals

残差分析是逻辑回归与线性回归的一个不同之处。与线性回归一样（参见图4-9），在 R 中计算偏残差非常简单：

1
2
3
4
5
6
7
8
9
10
11
terms <- predict(logistic_gam, type='terms')
partial_resid <- resid(logistic_model) + terms
df <- data.frame(payment_inc_ratio = loan_data[, 'payment_inc_ratio'],
terms = terms[, 's(payment_inc_ratio)'],
partial_resid = partial_resid[, 's(payment_inc_ratio)'])

ggplot(df, aes(x=payment_inc_ratio, y=partial_resid, solid = FALSE)) +
geom_point(shape=46, alpha=0.4) +
geom_line(aes(x=payment_inc_ratio, y=terms),
color='red', alpha=0.5, size=1.5) +
labs(y='Partial Residual')

由此产生的图表如图5-4所示。

F5.4

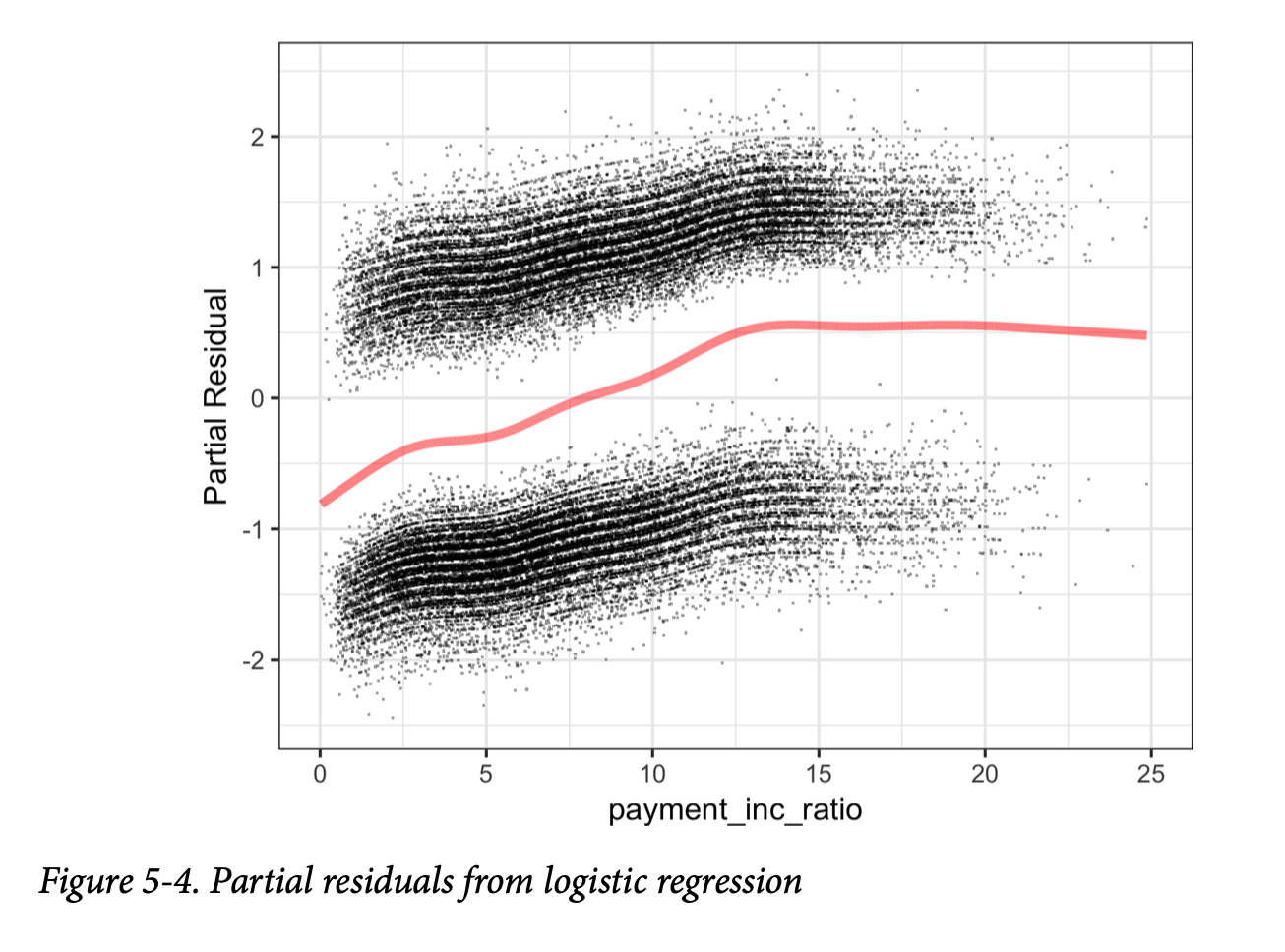
图中所示的估计拟合线穿过两组点云之间。顶部的点云对应于响应为1（违约贷款），底部的点云对应于响应为0（已还清贷款）。这对于逻辑回归的残差来说是非常典型的，因为其输出是二元的。预测值是以 logit（对数几率）来衡量的，它始终是一个有限值。而实际值（绝对的0或1）对应于无限的 logit（正或负），因此残差（被加到拟合值上）永远不会等于0。因此，在偏残差图中，绘制的点云始终位于拟合线上方或下方。尽管逻辑回归中的偏残差不如线性回归中那么有价值，但它们仍可用于确认非线性行为并识别高影响力的记录。

目前，在任何主要的 Python 包中都没有偏残差的实现。我们在随附的源代码仓库中提供了用于创建偏残差图的 Python 代码。

警告：

summary 函数的部分输出可以被忽略。离散参数不适用于逻辑回归，它是为其他类型的 GLM 准备的。残差偏差和评分迭代次数与最大似然拟合方法相关；参见第215页的“最大似然估计”。

关键思想

  • 相似性：逻辑回归与线性回归类似，但其结果变量是二元的。
  • 模型转换：需要进行几种转换，才能将模型转换为可以作为线性模型进行拟合的形式，其中响应变量是几率比的对数。
  • 反向映射：在模型（通过迭代过程）拟合后，对数几率被映射回一个概率。
  • 流行原因：逻辑回归之所以流行，是因为它计算速度快，并且产生的模型只需少量算术运算即可在新数据上进行评分。

评估分类模型

Evaluating Classification Models

对分类模型进行评估，通常是训练几个不同的模型，将它们分别应用于一个保留样本，并评估其性能。有时，在评估和调优了多个模型后，如果数据足够，会使用第三个、之前未使用的保留样本来估计所选模型在新数据上的表现。不同的学科和从业者也会使用验证（validation）和测试（test）这两个术语来指代保留样本。从根本上说，评估过程旨在确定哪个模型能产生最准确和最有用的预测。

评估分类模型的关键术语

  • 准确率（Accuracy） 正确分类的案例所占的百分比（或比例）。

  • 混淆矩阵（Confusion matrix） 一个表格显示（二元情况下为2×2），按预测和实际分类状态列出记录数量。

  • 灵敏度（Sensitivity） 所有实际为1的案例中，被正确分类为1的百分比（或比例）。 同义词：召回率（Recall）

  • 特异度（Specificity） 所有实际为0的案例中，被正确分类为0的百分比（或比例）。

  • 精确率（Precision） 所有被预测为1的案例中，实际为1的百分比（或比例）。

  • ROC曲线（ROC curve） 绘制灵敏度与特异度关系的图。

  • 提升度（Lift） 衡量模型在不同概率截止点下识别（相对罕见的）1的能力有多有效。

衡量分类性能的一个简单方法是计算正确预测的比例，即测量准确率（Accuracy）。准确率只是一个总误差的度量：

\[ \text{准确率} = \frac{\sum\text{True Positive} + \sum\text{True Negative}}{\text{样本量}} \] 在大多数分类算法中，每个案例都被分配一个“估计为1的概率”。默认的决策点，或截止点（cutoff），通常是0.50或50%。如果概率高于0.5，则分类为“1”；否则为“0”。另一个替代的默认截止点是数据中1的普遍概率。

混淆矩阵

Confusion Matrix

混淆矩阵是分类指标的核心。它是一个表格，按预测和实际结果的类别显示正确和不正确预测的数量。在 R 和 Python 中有许多可用的包来计算混淆矩阵，但在二元情况下，手动计算一个也很简单。

为了说明混淆矩阵，考虑在包含相同数量的违约和已还清贷款的平衡数据集上训练的 logistic_gam 模型（参见图5-4）。按照惯例，\(Y=1\) 对应于目标事件（例如，违约），而 \(Y=0\) 对应于负面（或常规）事件（例如，已还清）。以下代码在 R 中计算了应用于整个（不平衡）训练集的 logistic_gam 模型的混淆矩阵：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
pred <- predict(logistic_gam, newdata=train_set)
pred_y <- as.numeric(pred > 0)
true_y <- as.numeric(train_set$outcome=='default')
true_pos <- (true_y==1) & (pred_y==1)
true_neg <- (true_y==0) & (pred_y==0)
false_pos <- (true_y==0) & (pred_y==1)
false_neg <- (true_y==1) & (pred_y==0)
conf_mat <- matrix(c(sum(true_pos), sum(false_pos),
sum(false_neg), sum(true_neg)), 2, 2)
colnames(conf_mat) <- c('Yhat = 1', 'Yhat = 0')
rownames(conf_mat) <- c('Y = 1', 'Y = 0')
conf_mat

Yhat = 1 Yhat = 0
Y = 1 14295    8376
Y = 0 8052    14619

在 Python 中：

1
2
3
4
5
6
7
8
9
10
11
12
pred = logit_reg.predict(X)
pred_y = logit_reg.predict(X) == 'default'
true_y = y == 'default'
true_pos = true_y & pred_y
true_neg = ~true_y & ~pred_y
false_pos = ~true_y & pred_y
false_neg = true_y & ~pred_y
conf_mat = pd.DataFrame([[np.sum(true_pos), np.sum(false_neg)],
[np.sum(false_pos), np.sum(true_neg)]],
index=['Y = default', 'Y = paid off'],
columns=['Yhat = default', 'Yhat = paid off'])
conf_mat

预测结果是列，实际结果是行。矩阵的对角线元素显示了正确预测的数量，非对角线元素显示了不正确预测的数量。例如，有14,295笔违约贷款被正确预测为违约，但有8,376笔违约贷款被错误地预测为已还清。

图5-5显示了二元响应 \(Y\) 的混淆矩阵与不同指标之间的关系（关于这些指标的更多信息，请参阅第223页的“精确率、召回率和特异度”）。与贷款数据的示例一样，实际响应沿行排列，预测响应沿列排列。对角线上的框（左上、右下）显示了预测 \(Y\) 正确预测响应的情况。

F5.5

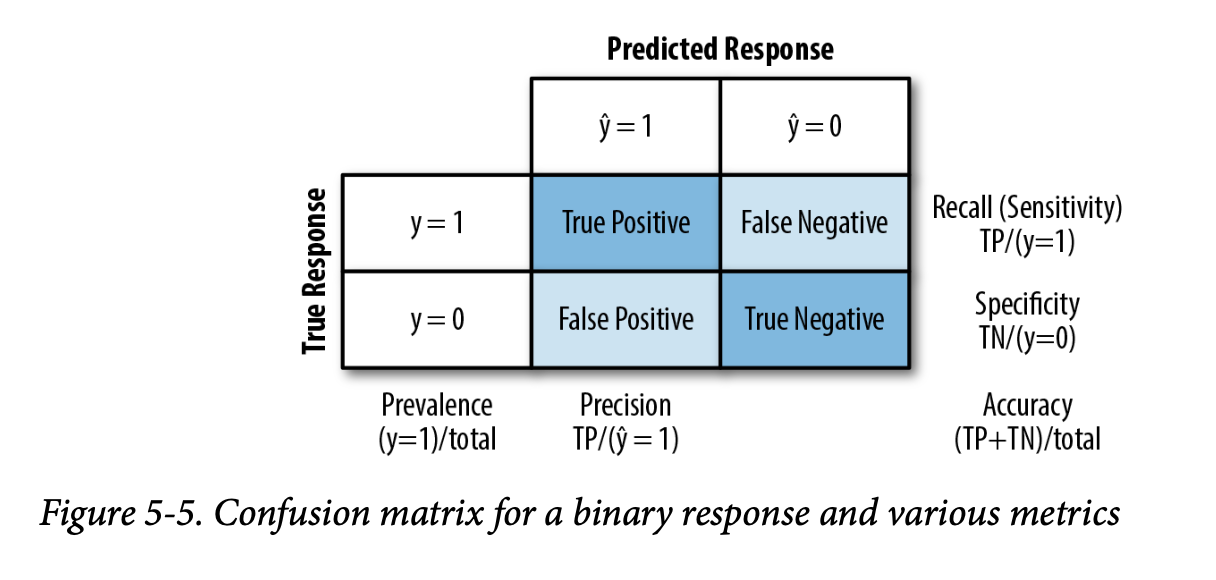
一个没有明确提及的重要指标是假阳性率（与精确率镜像）。当1s是罕见的类别时，假阳性与所有预测为阳性的比率可能很高，这导致一种不直观的情况：被预测为1的案例很可能实际上是0。这个问题困扰着广泛应用的医疗筛查测试（例如乳房X光检查）：由于病症相对罕见，阳性测试结果很可能并不意味着患有乳腺癌。这给公众带来了很大的困惑。

警告：

在这里，我们将实际响应沿行排列，预测响应沿列排列，但将其反转也很常见。一个值得注意的例子是 R 中流行的 caret 包。

罕见类别问题

The Rare Class Problem

在许多情况下，待预测的类别存在不平衡，其中一个类别比另一个更普遍，例如，合法的保险索赔与欺诈性索赔，或网站上的浏览者与购买者。罕见类别（例如，欺诈性索赔）通常是更受关注的类别，通常被指定为1，与更普遍的0形成对比。在典型场景中，1是更重要的案例，因为将其错误地分类为0的成本比将0错误地分类为1的成本更高。例如，正确识别一次欺诈性保险索赔可能节省数千美元。另一方面，正确识别一次非欺诈性索赔仅节省了你手动进行更仔细审查的成本和精力（如果该索赔被标记为“欺诈性”，你就会这样做）。

在这种情况下，除非类别很容易分离，否则最准确的分类模型可能是一个简单地将所有东西都分类为0的模型。例如，如果一个网站上只有0.1%的浏览者最终购买，那么一个预测每个浏览者都会离开而不会购买的模型将有99.9%的准确率。然而，它将毫无用处。相反，我们会乐于接受一个整体准确率较低，但善于识别购买者的模型，即使它在这个过程中错误地分类了一些非购买者。

精确率、召回率和特异度

Precision, Recall, and Specificity

除了纯粹的准确率之外，还有一些更细致的指标常用于评估分类模型。其中一些在统计学——特别是生物统计学——中有很长的历史，它们被用来描述诊断测试的预期性能。精确率（Precision）衡量预测为正向结果的准确性（参见图5-5）： \[ \text{精确率} = \frac{\sum\text{True Positive}}{\sum\text{True Positive} + \sum\text{False Positive}} \] 召回率（Recall），也称为灵敏度（Sensitivity），衡量模型预测正向结果的能力——它正确识别的1的比例（参见图5-5）。在生物统计学和医学诊断中，“灵敏度”这个术语使用得更多，而在机器学习社区中，“召回率”使用得更多。召回率的定义是： \[ \text{召回率} = \frac{\sum\text{True Positive}}{\sum\text{True Positive} + \sum\text{False Negative}} \] 另一个使用的指标是特异度（Specificity），它衡量模型预测负向结果的能力： \[ \text{特异度} = \frac{\sum\text{True Negative}}{\sum\text{True Negative} + \sum\text{False Positive}} \] 我们可以从 R 中的 conf_mat 计算这三个指标：

1
2
3
4
5
6
# precision
conf_mat[1, 1] / sum(conf_mat[,1])
# recall
conf_mat[1, 1] / sum(conf_mat[1,])
# specificity
conf_mat[2, 2] / sum(conf_mat[2,])

以下是 Python 中计算这些指标的等效代码：

1
2
3
4
5
6
conf_mat = confusion_matrix(y, logit_reg.predict(X))
print('Precision', conf_mat[0, 0] / sum(conf_mat[:, 0]))
print('Recall', conf_mat[0, 0] / sum(conf_mat[0, :]))
print('Specificity', conf_mat[1, 1] / sum(conf_mat[1, :]))
precision_recall_fscore_support(y, logit_reg.predict(X),
labels=['default', 'paid off'])

scikit-learn 有一个自定义方法 precision_recall_fscore_support，可以一次性计算出精确率和召回率/特异度。

ROC曲线

ROC Curve

你可以看到，召回率（recall）和特异度（specificity）之间存在一个权衡。捕获更多的1通常意味着将更多的0错误分类为1。一个理想的分类器应该在很好地分类1的同时，不会将更多的0错误分类为1。

捕捉这种权衡的指标是“受试者工作特征（Receiver Operating Characteristics）”曲线，通常简称为ROC曲线。ROC曲线将召回率（灵敏度）绘制在y轴上，特异度绘制在x轴上。ROC曲线显示了当你改变截止点来决定如何分类一条记录时，召回率和特异度之间的权衡关系。灵敏度（召回率）绘制在y轴上，而你可能会遇到两种形式的x轴标注：

  • x轴绘制特异度，左边是1，右边是0。
  • x轴绘制1-特异度，左边是0，右边是1。

无论哪种方式，曲线看起来都完全相同。计算ROC曲线的过程是：

  1. 排序：根据预测为1的概率对记录进行排序，从最有可能的开始，到最不可能的结束。
  2. 计算：基于排序后的记录，计算累积的特异度和召回率。

在 R 中计算 ROC 曲线非常简单。以下代码计算贷款数据的 ROC：

1
2
3
4
5
6
7
8
9
10
idx <- order(-pred)
recall <- cumsum(true_y[idx] == 1) / sum(true_y == 1)
specificity <- (sum(true_y == 0) - cumsum(true_y[idx] == 0)) / sum(true_y == 0)
roc_df <- data.frame(recall = recall, specificity = specificity)
ggplot(roc_df, aes(x=specificity, y=recall)) +
geom_line(color='blue') +
scale_x_reverse(expand=c(0, 0)) +
scale_y_continuous(expand=c(0, 0)) +
geom_line(data=data.frame(x=(0:100) / 100), aes(x=x, y=1-x),
linetype='dotted', color='red')

在 Python 中，我们可以使用 scikit-learn 函数 sklearn.metrics.roc_curve 来计算 ROC 曲线所需的信息。你也可以找到类似的 R 包，例如 ROCR：

1
2
3
4
5
6
7
8
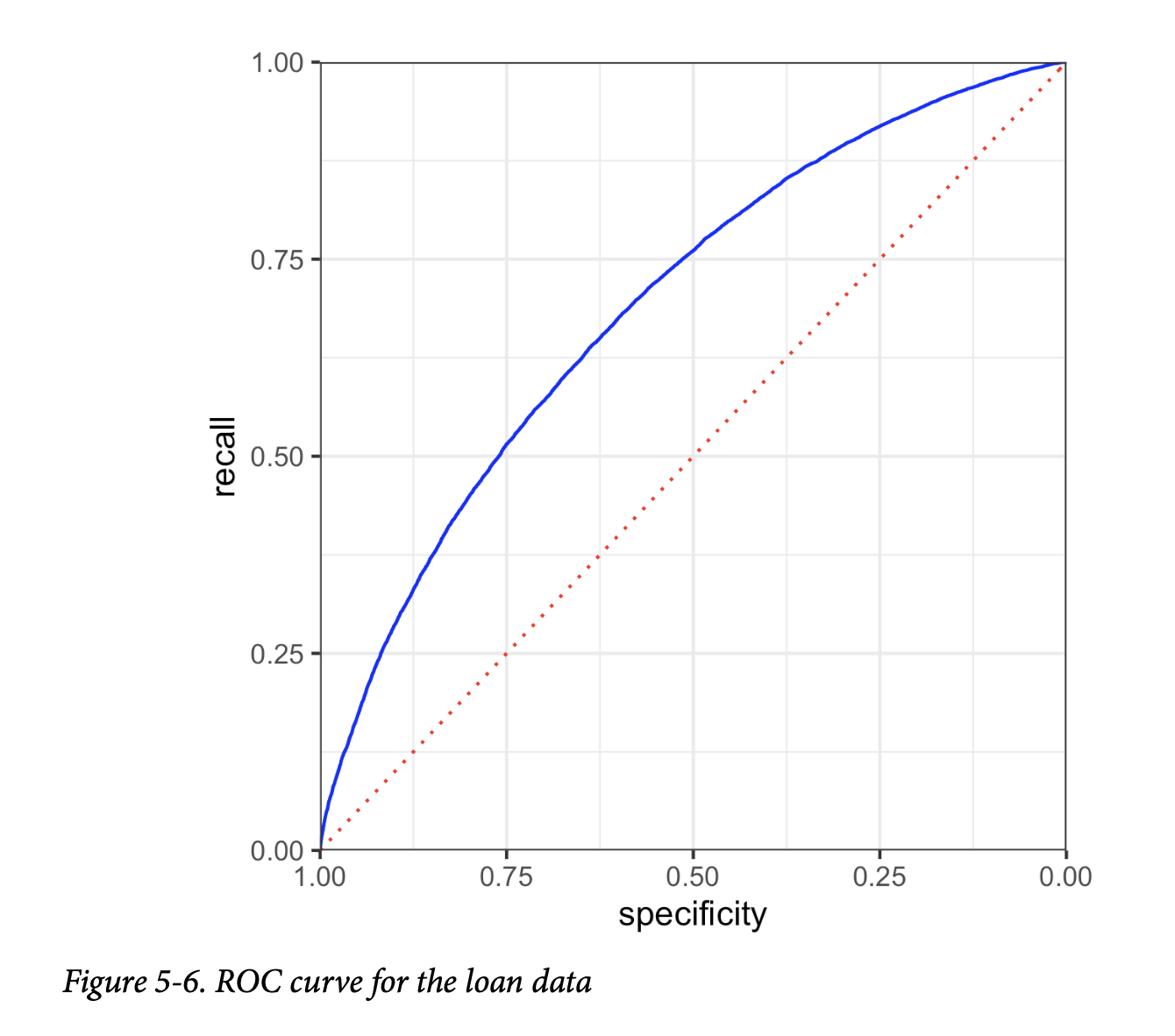
9
fpr, tpr, thresholds = roc_curve(y, logit_reg.predict_proba(X)[:,0],
pos_label='default')
roc_df = pd.DataFrame({'recall': tpr, 'specificity': 1 - fpr})
ax = roc_df.plot(x='specificity', y='recall', figsize=(4, 4), legend=False)
ax.set_ylim(0, 1)
ax.set_xlim(1, 0)
ax.plot((1, 0), (0, 1))
ax.set_xlabel('specificity')
ax.set_ylabel('recall')

结果如图5-6所示。虚线对角线对应于不比随机猜测好的分类器。一个极其有效的分类器（或者在医疗情境中，一个极其有效的诊断测试）的 ROC 曲线将紧贴左上角——它将正确识别大量的1，同时不会将大量的0错误分类为1。对于这个模型，如果我们想要一个特异度至少为50%的分类器，那么召回率约为75%。

F5.6

通用注解：

精确率-召回率曲线(Precision-Recall Curve)

除了 ROC 曲线之外，检查精确率-召回率（Precision-Recall, PR）曲线也很有启发性。PR 曲线以类似的方式计算，不同之处在于数据从最不可能到最有可能进行排序，并计算累积的精确率和召回率统计数据。PR 曲线在评估具有高度不平衡结果的数据时特别有用。

AUC (曲线下面积)

ROC曲线是一个有价值的图形工具，但它本身并不能构成衡量分类器性能的单一指标。然而，ROC曲线可以用来计算曲线下面积（Area Under the Curve, AUC）指标。AUC就是ROC曲线下的总面积。AUC的值越大，分类器越有效。一个AUC为1的分类器是完美的：它能正确分类所有1，并且不会将任何0错误地分类为1。一个完全无效的分类器——对角线——的AUC值为0.5。

F5.7

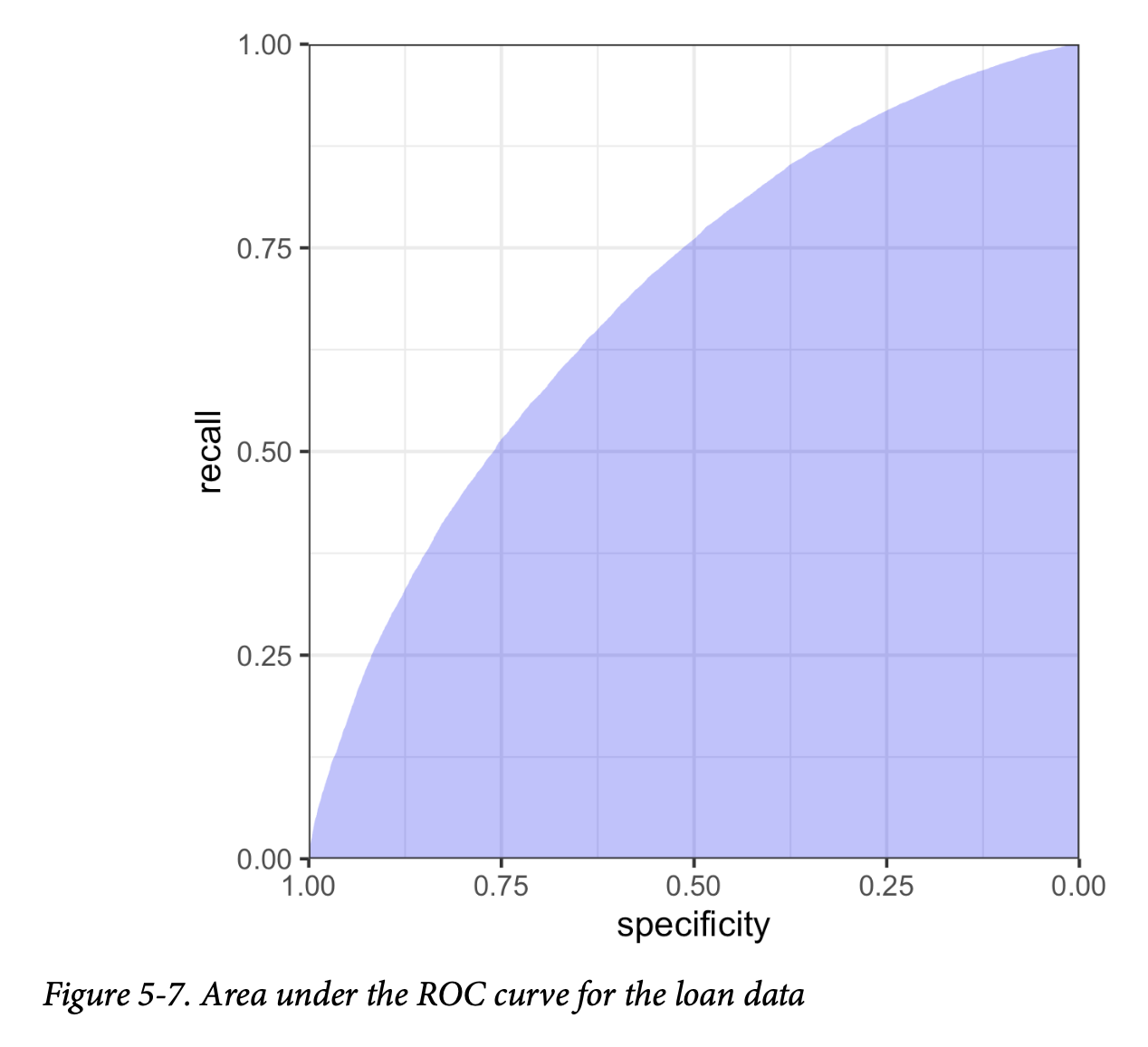
图5-7显示了贷款模型的ROC曲线下面积。在 R 中可以通过数值积分计算AUC值：

1
2
sum(roc_df$recall[-1] * diff(1 - roc_df$specificity))
[1] 0.6926172

在 Python 中，我们可以像 R 中那样计算准确率，也可以使用 scikit-learn 的 sklearn.metrics.roc_auc_score 函数。你需要提供0或1的期望值：

1
2
3
print(np.sum(roc_df.recall[:-1] * np.diff(1 - roc_df.specificity)))
print(roc_auc_score([1 if yi == 'default' else 0 for yi in y],
logit_reg.predict_proba(X)[:, 0]))

该模型的AUC约为0.69，这表明它是一个相对较弱的分类器。

警告：

假阳性率的混淆（False Positive Rate Confusion）

假阳性/假阴性率常常与特异度或灵敏度混淆或混为一谈（甚至在出版物和软件中也是如此！）。有时，假阳性率被定义为测试结果为阳性的真阴性样本的比例。在许多情况下（例如网络入侵检测），该术语被用来指代真阴性的阳性信号的比例。

提升度

Lift

使用 AUC 作为评估模型的指标，比简单的准确率有所改进，因为它能评估分类器在整体准确率和识别更重要的 1 之间的权衡处理得如何。但它没有完全解决罕见类别问题，在这种情况下，你需要将模型的概率截止点降低到0.5以下，以避免所有记录都被分类为0。在这种情况下，一条记录被分类为1的概率可能低至0.4、0.3甚至更低就足够了。实际上，我们最终会过度识别1，以体现它们更高的重要性。

改变这个截止点会增加你捕捉到1的机会（代价是将更多的0错误地分类为1）。但最佳的截止点在哪里呢？

提升度（Lift）的概念让你能够推迟回答这个问题。相反，它让你按照记录被预测为1的概率顺序来考虑它们。例如，在被分类为1的记录中，如果取概率最高的10%作为子集，那么与盲目随机挑选的基准相比，算法的表现要好多少？如果你在这个最高的十分位数中能得到0.3%的响应率，而不是随机挑选得到的0.1%的整体响应率，那么该算法在这个十分位数中的提升度（也称为增益）就是3。提升度图（增益图）将这种效果量化到整个数据范围内。它可以按十分位数生成，也可以在数据的整个范围内连续生成。

要计算提升度图，首先要生成一个累积增益图（cumulative gains chart），该图将召回率绘制在y轴上，记录总数绘制在x轴上。提升度曲线是累积增益与代表随机选择的对角线之间的比率。十分位增益图是预测建模中最古老的技术之一，其历史可以追溯到互联网商业出现之前。它们在直邮营销专业人士中特别受欢迎。如果无差别地应用，直邮是一种昂贵的广告方式，因此广告商会使用预测模型（在早期非常简单）来识别最有可能获得回报的潜在客户。

警告：

Uplift

有时，uplift 一词与 lift 含义相同。但在一个更受限的情境中，它有一个不同的含义，即当进行 A/B 测试，并将处理方式（A或B）用作预测模型中的预测变量时。Uplift 是预测模型对于单个案例使用处理A与处理B相比，其响应的改进程度。这是通过对单个案例进行两次评分来确定的：第一次将预测变量设置为A，然后再次将其切换为B。营销人员和政治竞选顾问使用这种方法来决定哪种信息处理方式应该用于哪些客户或选民。

提升度曲线让你能够观察设定不同概率截止点来将记录分类为1所带来的后果。它可以作为确定适当截止水平的中间步骤。例如，税务机关可能只有一定数量的资源用于税务审计，并希望将这些资源用于最有可能偷税漏税的人。考虑到资源限制，该机构会使用提升度图来估算在哪里划定界限，决定哪些报税表将被选中进行审计，哪些将被放过。

关键思想

  • 准确率（正确分类的百分比）仅仅是评估模型的第一步。
  • 其他指标（召回率、特异度和精确率）侧重于更具体的性能特征（例如，召回率衡量模型正确识别1的能力）。
  • AUC（ROC曲线下面积）是衡量模型区分1和0能力的一个常用指标。
  • 同样，提升度衡量模型识别1的有效性，通常按十分位数计算，从最有可能的1开始。

不平衡数据的策略

Strategies for Imbalanced Data

上一节讨论了使用超越简单准确率的指标来评估分类模型，这些指标适用于不平衡数据——即目标结果（网站购买、保险欺诈等）非常罕见的数据。本节将探讨可用于改善不平衡数据下预测建模性能的其他策略。

不平衡数据的关键术语

  • 欠采样（Undersample） 在分类模型中使用较少数量的普遍类别记录。 同义词：降采样（Downsample）

  • 过采样（Oversample） 在分类模型中使用更多数量的罕见类别记录，如果需要，可通过自举法实现。 同义词：升采样（Upsample）

  • 上加权或下加权（Up weight or down weight） 在模型中对罕见（或普遍）类别赋予更多（或更少）的权重。

  • 数据生成（Data generation） 类似于自举法，但每个新的自举记录都与原始记录略有不同。

  • z分数（z-score） 标准化后得到的值。

  • K 在最近邻计算中考虑的邻居数量。

欠采样

Undersampling

如果你有足够的数据，就像贷款数据一样，一种解决方案是对普遍类别进行欠采样（或降采样），这样建模数据在0和1之间会更平衡。欠采样的基本思想是，主导类的数据包含许多冗余记录。处理一个更小、更平衡的数据集，有助于提高模型性能，并使数据准备、模型探索和试运行变得更容易。

多少数据才算足够？这取决于应用，但通常来说，对于较不主导的类别，拥有数万条记录就足够了。1与0之间越容易区分，所需的数据就越少。

第208页“逻辑回归”中分析的贷款数据基于一个平衡的训练集：一半贷款已还清，另一半已违约。预测值也类似：一半的概率小于0.5，另一半大于0.5。在完整的（不平衡）数据集中，只有大约19%的贷款是违约的，如R代码所示：

1
2
mean(full_train_set$outcome=='default')
[1] 0.1889455

在Python中：

1
2
print('percentage of loans in default: ',
100 * np.mean(full_train_set.outcome == 'default'))

如果我们使用完整的数据集来训练模型，会发生什么？让我们看看在R中会是什么样子：

1
2
3
4
5
6
full_model <- glm(outcome ~ payment_inc_ratio + purpose_ + home_ +
emp_len_+ dti + revol_bal + revol_util,
data=full_train_set, family='binomial')
pred <- predict(full_model)
mean(pred > 0)
[1] 0.003942094

在Python中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
predictors = ['payment_inc_ratio', 'purpose_', 'home_', 'emp_len_',
'dti', 'revol_bal', 'revol_util']
outcome = 'outcome'
X = pd.get_dummies(full_train_set[predictors], prefix=
drop_first=True)
''
, prefix_sep=
''
,
y = full_train_set[outcome]
full_model = LogisticRegression(penalty='l2', C=1e42, solver='liblinear')
full_model.fit(X, y)
print('percentage of loans predicted to default: ',
100 * np.mean(full_model.predict(X) == 'default'))

只有0.39%的贷款被预测为违约，不到预期数量的1/47。已还清的贷款压倒性地盖过了违约贷款，因为模型在训练时对所有数据给予了同等的权重。直观地思考，存在如此多的未违约贷款，加上预测变量数据中不可避免的变异性，这意味着，即使对于一笔违约贷款，模型也可能偶然找到一些与它相似的未违约贷款。当使用平衡样本时，大约50%的贷款被预测为违约。

过采样和上/下加权

Oversampling and Up/Down Weighting

对欠采样方法的一种批评是，它丢弃了数据，没有利用手头的所有信息。如果你的数据集相对较小，且稀有类别只包含几百或几千条记录，那么对主导类别进行欠采样可能会丢失有用的信息。在这种情况下，你应该过采样（或升采样）稀有类别，通过带放回抽样（自举法）来增加额外的行。

你也可以通过加权数据来达到类似的效果。许多分类算法都接受一个权重参数，允许你对数据进行上/下加权。例如，在 R 中使用 glm 函数的 weight 参数，对贷款数据应用一个权重向量：

1
2
3
4
5
6
7
8
wt <- ifelse(full_train_set$outcome=='default',
1 / mean(full_train_set$outcome == 'default'), 1)
full_model <- glm(outcome ~ payment_inc_ratio + purpose_ + home_ +
emp_len_+ dti + revol_bal + revol_util,
data=full_train_set, weight=wt, family='quasibinomial')
pred <- predict(full_model)
mean(pred > 0)
[1] 0.5767208

大多数 scikit-learn 方法允许在 fit 函数中使用 sample_weight 关键字参数来指定权重：

1
2
3
4
5
6
7
default_wt = 1 / np.mean(full_train_set.outcome == 'default')
wt = [default_wt if outcome == 'default' else 1
for outcome in full_train_set.outcome]
full_model = LogisticRegression(penalty="l2", C=1e42, solver='liblinear')
full_model.fit(X, y, sample_weight=wt)
print('percentage of loans predicted to default (weighting): ',
100 * np.mean(full_model.predict(X) == 'default'))

对于违约贷款，权重被设置为 \(1/p\)，其中 \(p\) 是违约的概率。未违约贷款的权重为1。违约贷款和未违约贷款的权重总和大致相等。现在预测值的均值约为58%，而不是0.39%。

请注意，加权提供了过采样稀有类别和欠采样主导类别的替代方案。

通用注解：

调整损失函数（Adapting the Loss Function）

许多分类和回归算法都优化某个特定标准或损失函数。例如，逻辑回归试图最小化偏差（deviance）。在文献中，有人提出修改损失函数以避免由稀有类别引起的问题。在实践中，这很难做到：分类算法可能很复杂且难以修改。加权是一种改变损失函数的简单方法，它降低了低权重记录的错误对模型的影响，从而倾向于高权重记录。

数据生成

Data Generation

数据生成是通过扰动现有记录来创建新记录，是利用自举法进行过采样的一种变体（参见第232页的“过采样和上/下加权”）。这一想法的直觉在于，由于我们只观察到有限的实例集，算法没有足够丰富的信息来构建分类“规则”。通过创建与现有记录相似但不完全相同的新记录，算法有机会学习到一套更健壮的规则。这种思想在精神上类似于集成统计模型（ensemble statistical models），例如提升法（boosting）和装袋法（bagging）（参见第6章）。

随着 SMOTE 算法（“合成少数类过采样技术”的缩写）的发布，这一想法得到了推广。SMOTE 算法会找到一条与被过采样的记录相似的记录（参见第238页的“K-最近邻”），并创建一个合成记录，该记录是原始记录和相邻记录的随机加权平均值，其中权重是针对每个预测变量单独生成的。创建的合成过采样记录的数量取决于所需的过采样比率，以使数据集在结果类别上达到大致平衡。

在 R 中有几个 SMOTE 的实现。处理不平衡数据最全面的包是 unbalanced。它提供了多种技术，包括一个用于选择最佳方法的“Racing”算法。然而，SMOTE 算法本身足够简单，可以使用 FNN 包在 R 中直接实现。

Python 包 imbalanced-learn 实现了一系列方法，其 API 与 scikit-learn 兼容。它提供了各种过采样和欠采样的方法，并支持将这些技术与提升法和装袋法分类器结合使用。

基于成本的分类

Cost-Based Classification

在实践中，准确率和 AUC 是选择分类规则的一种简陋方式。通常，可以为假阳性与假阴性分配一个估计成本，更合适的方法是结合这些成本来确定分类1和0时的最佳截止点。例如，假设一笔新贷款违约的预期成本为 \(C\)，而一笔已还清贷款的预期回报为 \(R\)。那么该笔贷款的预期回报（expected return）是：

\[ 预期回报 = P(Y=0) \times R + P(Y=1) \times C \] 与其简单地将一笔贷款标记为违约或已还清，或者确定违约概率，更有意义的是确定该笔贷款是否具有正的预期回报。预测的违约概率是一个中间步骤，必须将其与贷款的总价值结合起来，以确定预期利润，这才是业务的最终规划指标。例如，一笔价值较小的贷款可能会被放弃，而选择一笔价值较大但预测违约概率稍高的贷款。

探索预测结果

Exploring the Predictions

仅仅一个单一的指标，例如AUC，无法评估模型对特定情况的适用性的所有方面。图5-8展示了针对贷款数据，仅使用两个预测变量：borrower_score 和 payment_inc_ratio，拟合的四种不同模型的决策规则。这些模型包括：线性判别分析（LDA）、逻辑线性回归、使用广义加性模型（GAM）拟合的逻辑回归，以及一个树模型（参见第249页的“树模型”）。图中线左上方的区域对应于预测违约。在这种情况下，LDA 和逻辑线性回归的结果几乎相同。树模型产生了最不规则的规则，呈现出两个台阶。最后，逻辑回归的 GAM 拟合代表了树模型和线性模型之间的折中。

F5.8

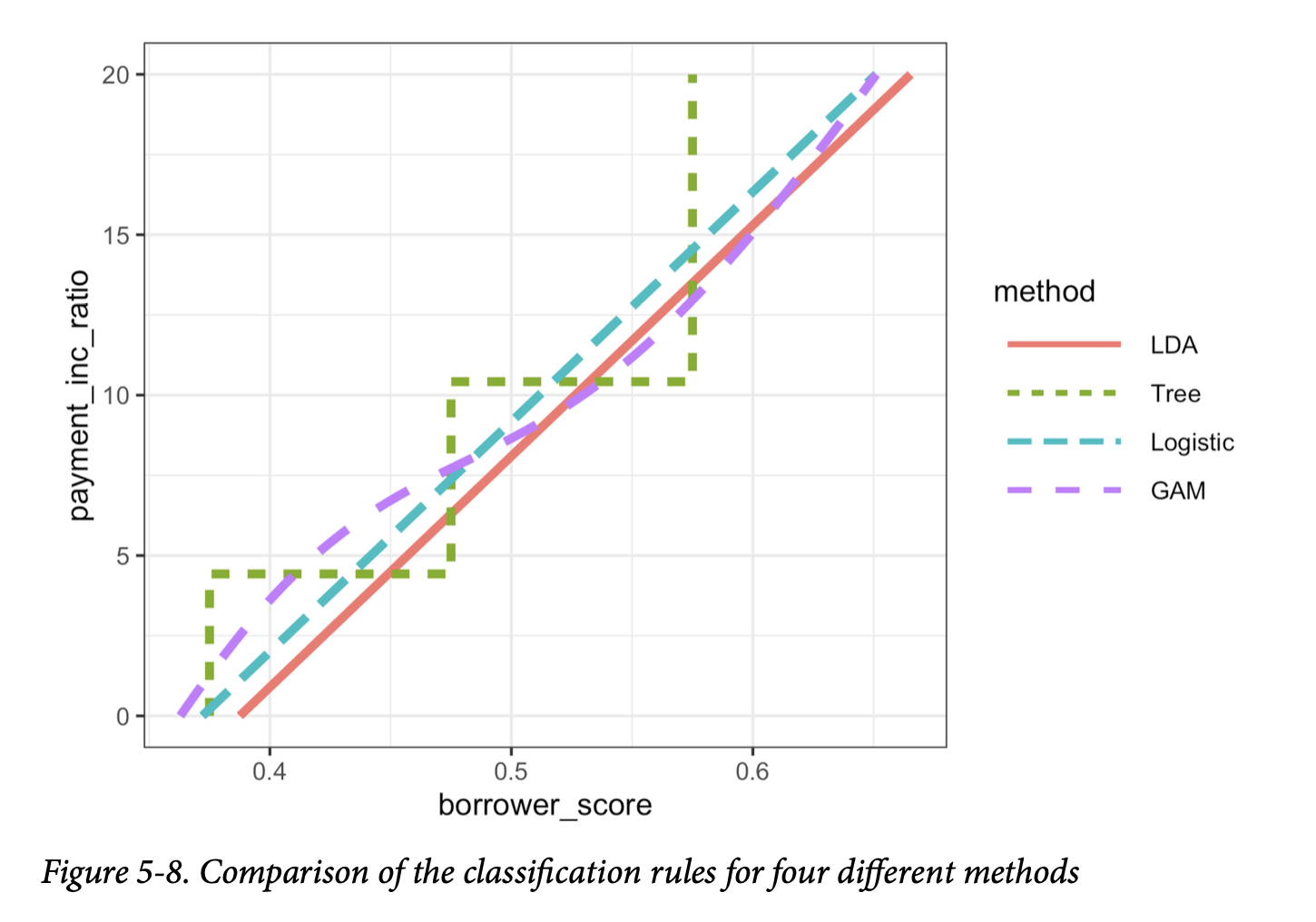
在更高维度中，或者在 GAM 和树模型的情况下，即使是生成这些规则的区域，也不容易可视化。

无论如何，对预测值进行探索性分析总是值得的。

关键思想

  • 高度不平衡的数据（即，感兴趣的结果，即1，很罕见）对于分类算法来说是有问题的。
  • 处理不平衡数据的一种策略是，通过欠采样多数类别（或过采样稀有类别）来平衡训练数据。
  • 如果使用了所有1s后仍然太少，你可以对稀有类别进行自举，或使用 SMOTE 来创建与现有稀有案例相似的合成数据。
  • 不平衡数据通常意味着正确分类某个类别（即1s）具有更高的价值，而这种价值比率应该被纳入评估指标中。

总结

分类，即预测一条记录属于两个或多个类别中的哪一个，是预测分析的一个基本工具。一笔贷款会违约吗（是或否）？它会提前还款吗？一个网站访问者会点击链接吗？他们会购买东西吗？一笔保险索赔是欺诈性的吗？在分类问题中，通常有一个类别是主要关注的（例如，欺诈性的保险索赔），在二元分类中，这个类别被指定为1，而另一个更普遍的类别为0。通常，这个过程的一个关键部分是估计倾向得分，即属于目标类别的概率。一个常见的情景是，感兴趣的类别相对罕见。在评估分类器时，有多种超越简单准确率的模型评估指标；当所有记录都分类为0也能产生高准确率时，这些指标在稀有类别情境下尤为重要。