第4章 回归与预测

发表于 分类于

《Practical Statistics for Data Scientists》书籍英文版
《面向数据科学家的实用统计学》中文版书籍

第 4 章 回归与预测

在统计学中，也许最常见的目标就是回答这样的问题：“变量 X（或者更常见地，X₁, …, Xₚ）是否与变量 Y 有关联？如果有，这种关系是什么，我们能否利用它来预测 Y？”

在预测领域——特别是基于其他“预测变量”的值来预测一个结果（目标）变量——统计学与数据科学的联系最为紧密。这一过程是在结果已知的数据上训练模型，以便随后将其应用于结果未知的数据，称为监督学习。数据科学与统计学的另一个重要交叉领域是异常检测：最初用于数据分析和改进回归模型的回归诊断方法，也可用来检测异常记录。

简单线性回归

简单线性回归提供了一个描述两个变量大小之间关系的模型。例如，随着 X 增大，Y 也增大；或者随着 X 增大，Y 减小。相关系数是衡量两个变量如何相关的另一种方式（见第 30 页“相关”一节）。不同的是，相关系数衡量的是两个变量之间联系的强度，而回归则量化了这种关系的具体形式。

简单线性回归的关键术语

响应变量（Response） 我们试图预测的变量。 同义词：因变量、Y 变量、目标、结果

​ dependent variable, Y variable, target, outcome

自变量（Independent variable） 用于预测响应变量的变量。 同义词：X 变量、特征、属性、预测变量

​ X variable, feature, attribute, predictor

记录（Record） 某个具体个体或案例的预测变量与结果变量值构成的向量。 同义词：行、案例、实例、样本

截距（Intercept） 回归直线的截距，即当 X = 0 时预测的值。 同义词：b₀、β₀

回归系数（Regression coefficient） 回归直线的斜率。 同义词：斜率、b₁、β₁、参数估计、权重

拟合值（Fitted values） 从回归直线得到的 Ŷᵢ 的估计值。 同义词：预测值

残差（Residuals） 观测值与拟合值之间的差异。 同义词：误差

​ errors

最小二乘法（Least squares） 通过最小化残差平方和来拟合回归的方法。 同义词：普通最小二乘、OLS

回归方程

The Regression Equation

简单线性回归估计当 X 发生一定变化时，Y 会改变多少。在相关系数中，变量 X 和 Y 是可以互换的；而在回归分析中，我们试图利用线性关系（即一条直线）由 X 预测 Y 变量： \[ Y = b_0 + b_1X \]

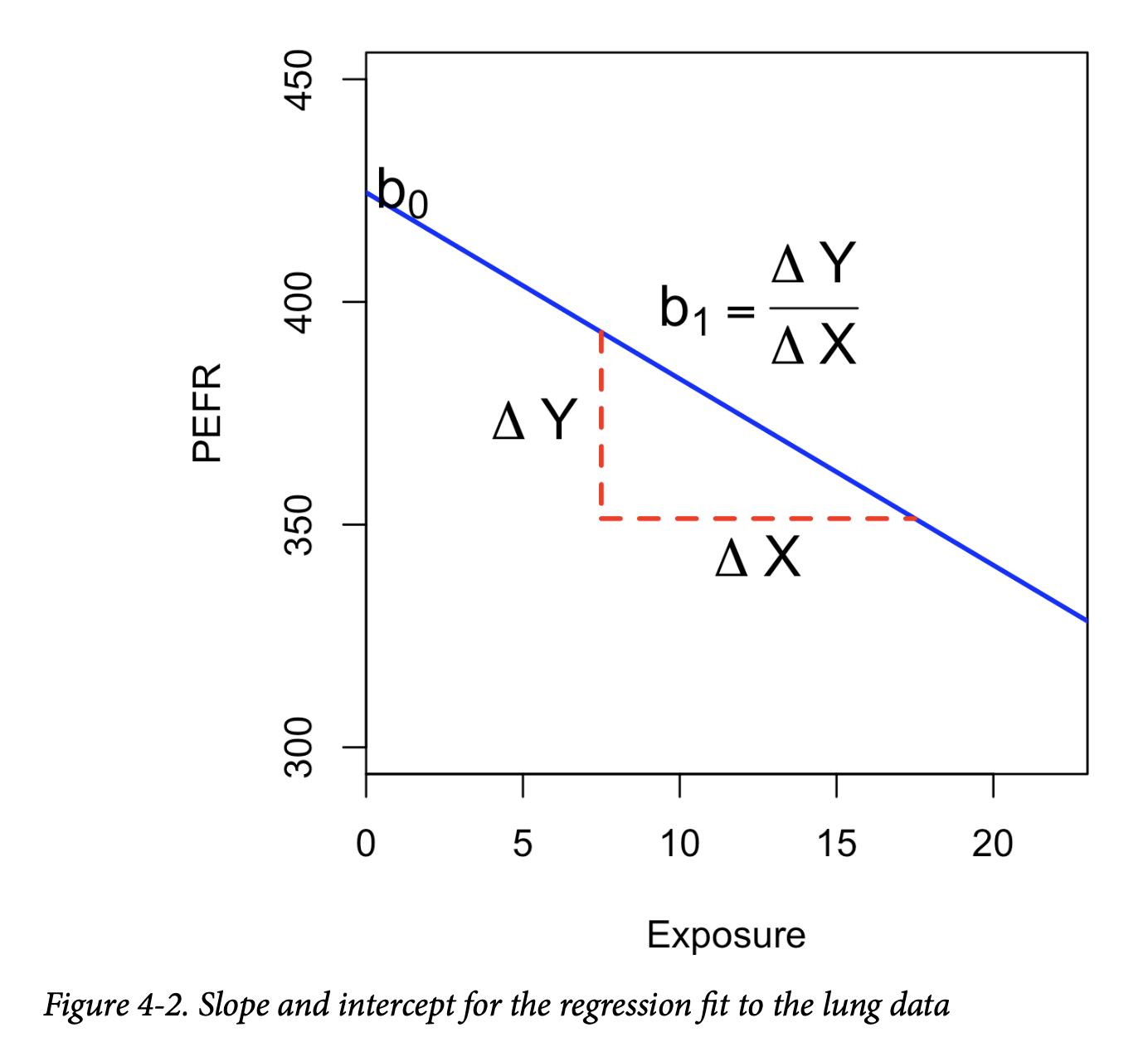
我们读作：“Y 等于 b₁ 乘以 X，再加上一个常数 b₀”。符号 b₀ 称为截距（或常数），符号 b₁ 称为 X 的斜率。在 R 的输出中，两者都显示为系数，不过在一般用法中，“系数”这一术语通常只指 b₁。Y 变量称为响应变量或因变量，因为它依赖于 X；X 变量称为预测变量或自变量。机器学习领域倾向于用其他术语，把 Y 称为“目标（target）”，把 X 称为“特征向量（feature vector）”。在本书中，我们将“预测变量（predictor）”和“特征（feature）”两个词交替使用。

F4.1

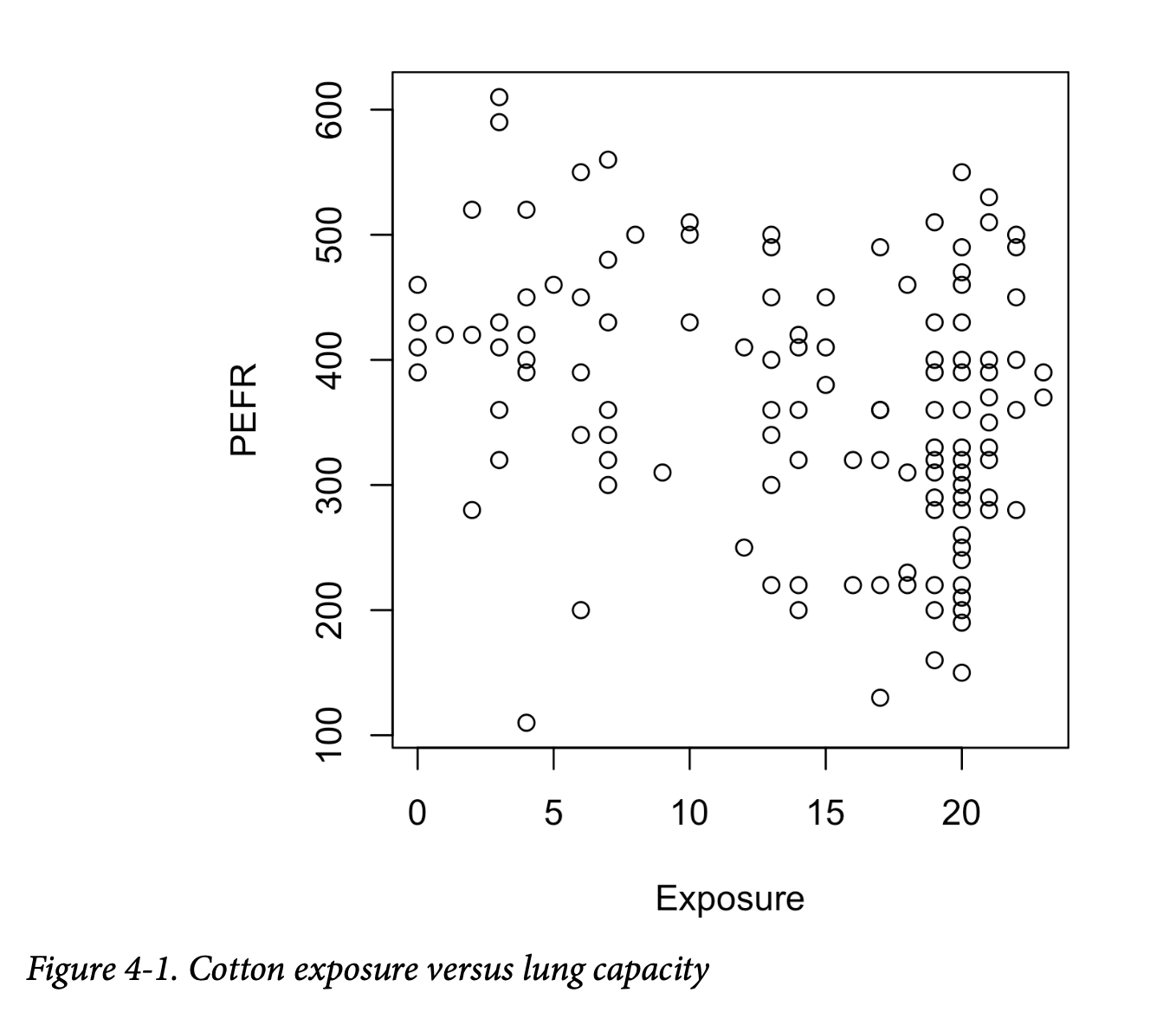
请看图 4-1 中的散点图，显示工人接触棉尘的年数（Exposure）与肺活量指标（PEFR 或“呼气峰流速”）之间的关系。PEFR 与 Exposure 的关系如何？仅从图上很难判断。

简单线性回归试图找到一条“最佳”的直线，用来预测响应变量 PEFR 作为预测变量 Exposure 的函数：

\[ \text{PEFR} = b_0 + b_1\text{Exposure} \]

在 R 中可以用 lm 函数拟合线性回归模型：

1
model <- lm(PEFR ~ Exposure, data=lung)

lm 表示 “linear model”，波浪号 ~ 表示“由 Exposure 预测 PEFR”。在这种模型定义下，截距会自动包含并拟合。如果想排除截距，需要这样写：

1
PEFR ~ Exposure - 1

打印模型对象得到如下输出：

1
2
3
4
5
6
Call:
lm(formula = PEFR ~ Exposure, data = lung)

Coefficients:
(Intercept)   Exposure
   424.583     -4.185

其中截距 b₀ = 424.583，可以解释为“工人接触棉尘年数为 0 时预测的 PEFR”。回归系数 b₁ = -4.185 可以解释为：“工人每多接触棉尘一年，PEFR 测量值平均减少 4.185”。

在 Python 中，可以使用 scikit-learn 包的 LinearRegression。（statsmodels 包也有一个与 R 类似的线性回归实现 sm.OLS，我们将在本章后面使用它）：

1
2
3
4
5
6
predictors = ['Exposure']
outcome = 'PEFR'
model = LinearRegression()
model.fit(lung[predictors], lung[outcome])
print(f'Intercept: {model.intercept_:.3f}')
print(f'Coefficient Exposure: {model.coef_[0]:.3f}')

该模型得到的回归直线如图 4-2 所示。

F4.2

拟合值与残差

Fitted Values and Residuals

回归分析中的重要概念是拟合值（预测值the predictions）和残差（预测误差 prediction errors）。一般情况下，数据不会完全落在一条直线上，所以回归方程应包含一个显式的误差项 \(e_i\)：

\[ Y_i = b_0 + b_1X_i + e_i \]

拟合值（也称预测值）通常记作 \(\hat{Y}_i\)（Y-hat），其表达式为：

\[ \hat{Y}_i = b_0 + b_1X_i \]

这里的 \(b_0\) 和 \(b_1\) 表示系数是估计值，而不是已知值。

知识点：

“帽子”符号（hat notation）用来区分估计值与真实值。因此，符号 \(\hat{b}\)（“b-hat”）是未知参数 \(b\) 的估计值。统计学家之所以要区分估计值和真实值，是因为估计值有不确定性，而真实值是固定的。

我们通过原始数据减去预测值来计算残差 \(e_i\)：

\[ e_i = Y_i - \hat{Y}_i \]

在 R 中，可以用 predict 和 residuals 函数获得拟合值和残差：

1
2
fitted <- predict(model)
resid <- residuals(model)

在 scikit-learn 的 LinearRegression 模型中，可以用 predict 方法在训练数据上获得拟合值，再计算残差。这是 scikit-learn 中所有模型的通用模式：

1
2
fitted = model.predict(lung[predictors])
residuals = lung[outcome] - fitted

图 4-3 展示了肺活量数据回归直线的残差。残差就是从数据点到回归直线的垂直虚线的长度。

F4.3

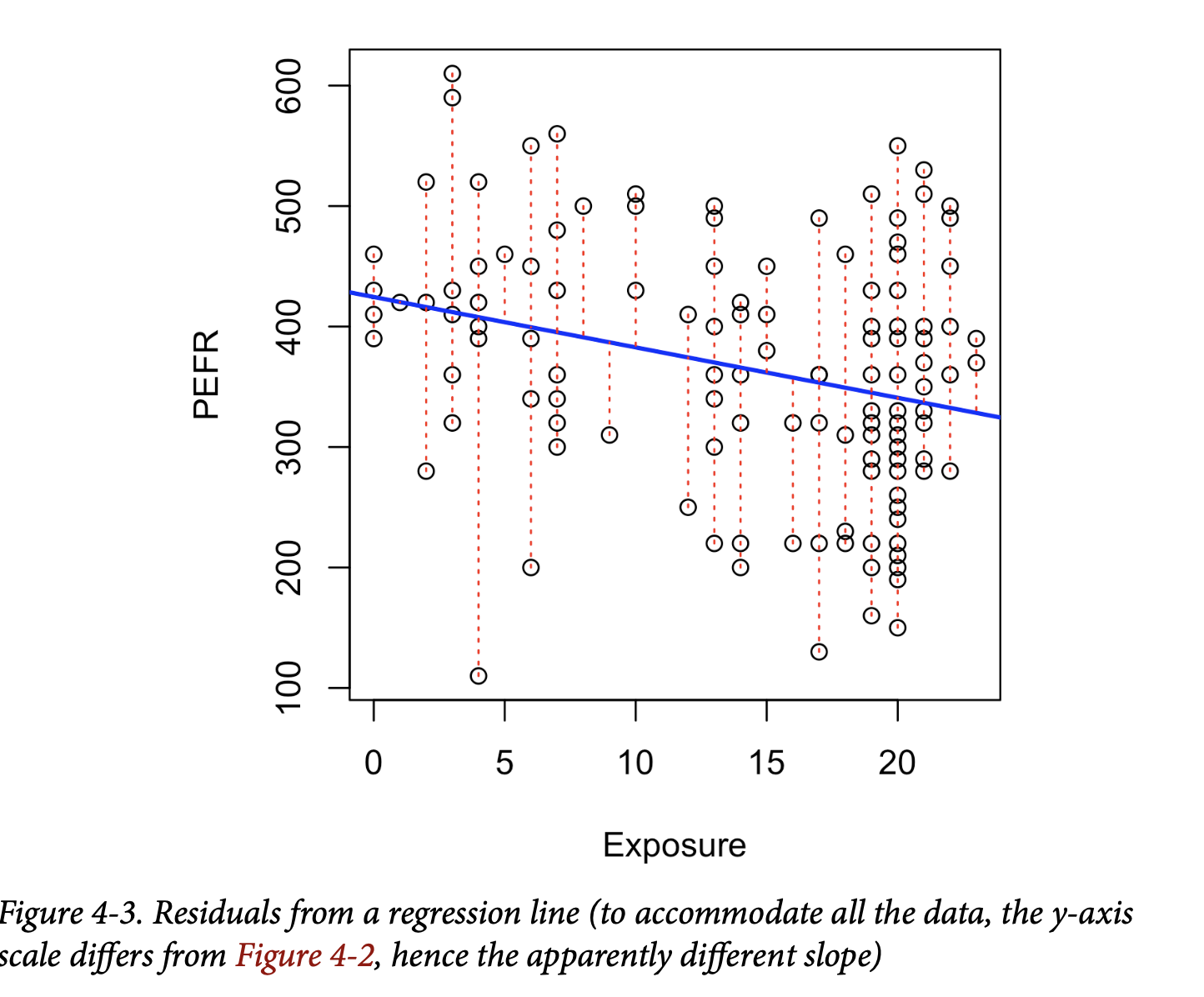
最小二乘法

Least Squares

那么模型是如何拟合数据的？当关系很明显时，你可以想象手工拟合一条直线。实际上，回归直线是通过最小化残差平方和（RSS, residual sum of squares）来估计的：

\[ \text{RSS}=\sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2 =\sum_{i=1}^{n}(Y_i - b_0 - b_1X_i)^2 \]

\(b_0\) 和 \(b_1\) 的估计值是使 RSS 最小的数值。

最小化残差平方和的方法称为最小二乘回归（least squares regression），或普通最小二乘回归（ordinary least squares, OLS）。这种方法常被归功于德国数学家高斯（Carl Friedrich Gauss），但实际上是由法国数学家勒让德（Adrien-Marie Legendre）在 1805 年首次发表的。最小二乘回归可以通过任何标准统计软件快速、方便地计算。

从历史上看，计算便利性是最小二乘法在回归中广泛应用的原因之一。在大数据时代，计算速度仍然是重要因素。最小二乘法对异常值敏感（就像均值一样，见第 10 页的“中位数与稳健估计”），不过这通常只在小型或中等规模数据集里才是个显著问题。有关回归中异常值的讨论见第 177 页“异常值”。

通用注解

回归术语：当分析师和研究人员单独使用“回归”这个词时，通常指的是线性回归，重点是建立一个线性模型来解释预测变量与数值型结果变量之间的关系。在正式的统计学意义上，回归还包括非线性模型，即预测变量与结果变量之间存在某种函数关系的模型。在机器学习领域，“回归”这个词有时也被宽泛地用来指任何输出连续数值型预测的模型（而相对于分类**方法，分类预测的是二元或类别型结果）。

预测与解释（画像分析）

Prediction Versus Explanation (Profiling)

从历史上看，回归分析的主要用途是揭示预测变量与结果变量之间的线性关系。目标是理解这种关系，并用拟合回归的数据来解释它。在这种情况下，主要关注的是回归方程中估计的斜率 \(b\)。经济学家想知道消费者支出与 GDP 增长之间的关系；公共卫生官员可能想了解一项公共宣传活动是否在促进安全性行为方面有效。在这些例子中，重点不是预测单个案例，而是理解变量之间的总体关系。

随着大数据的出现，回归被广泛用于为新数据预测个体结果（即建立预测模型），而不是解释手头的数据。在这种情况下，主要关注的是拟合值 \(\hat{Y}\)。在市场营销中，回归可用于预测广告投放规模变化带来的收入变化；大学利用回归预测学生的 GPA 与其 SAT 分数之间的关系。

一个拟合良好的回归模型表明，当 \(X\) 发生变化时，\(Y\) 也会随之变化。然而，仅凭回归方程并不能证明因果方向。因果推论必须基于对关系更广泛的理解。例如，回归方程可能显示网页广告点击数与转化数之间存在显著关系。得出“点击广告导致销售”而不是“销售导致点击”的结论，是基于我们对营销过程的知识，而非回归方程本身。

关键要点

  • 回归方程将响应变量 \(Y\) 与预测变量 \(X\) 的关系建模为一条直线。
  • 回归模型产生拟合值和残差——即响应的预测值以及预测误差。
  • 回归模型通常通过最小二乘法来拟合。
  • 回归既可用于预测，也可用于解释。

多元线性回归

Multiple Linear Regression

当有多个预测变量时，方程可以扩展为： \[ Y = b_0 + b_1 X_1 + b_2 X_2 + \dots + b_p X_p + e \]

此时不再是一条直线，而是一个线性模型——每个系数与其变量（特征）之间的关系是线性的。

多元线性回归关键术语

  • 均方根误差（Root mean squared error, RMSE） 回归平均平方误差的平方根（这是比较回归模型最广泛使用的指标）。

  • 残差标准误（Residual standard error, RSE） 与均方根误差相同，但对自由度进行了调整。

  • R 平方（R-squared, \(R^2\)） 模型解释的方差比例，从 0 到 1。 同义词：决定系数（coefficient of determination）。

  • t 统计量（t-statistic） 某个预测变量系数除以其标准误差，提供衡量模型中变量重要性的指标（参见第 110 页 “t 检验”）。

  • 加权回归（Weighted regression） 对不同记录赋予不同权重的回归。

简单线性回归中的其他概念（如最小二乘拟合、拟合值和残差的定义）都可以推广到多元线性回归。例如，拟合值为：

\[ \hat{Y}_i = b_0 + b_1 X_{1,i} + b_2 X_{2,i} + \dots + b_p X_{p,i} \]

示例

King County房屋数据

多元线性回归的一个示例是估计房屋价值。县评估员需要估算房屋的价值以评税；房地产专业人士和购房者会参考 Zillow 等流行网站来判断一个公平价格。下面是来自美国华盛顿州金县（西雅图）的房屋数据（house 数据框）的一些行：

1
2
head(house[, c('AdjSalePrice', 'SqFtTotLiving', 'SqFtLot', 'Bathrooms',
'Bedrooms', 'BldgGrade')])

数据来源：本地数据框 [6 x 6]

AdjSalePrice (int) SqFtTotLiving (dbl) SqFtLot (int) Bathrooms (int) Bedrooms (dbl) BldgGrade (int)
1 300805 2400 9373 3.00 6
2 1076162 3764 20156 3.75 4
3 761805 2060 26036 1.75 4
4 442065 3200 8618 3.75 5
5 297065 1720 8620 1.75 4
6 411781 930 1012 1.50 2

在 pandas 中，head 方法同样列出前几行：

1
2
3
subset = ['AdjSalePrice', 'SqFtTotLiving', 'SqFtLot', 'Bathrooms',
'Bedrooms', 'BldgGrade']
house[subset].head()

我们的目标是用其它变量预测销售价格。R 语言的 lm 函数通过在公式右边加入更多变量就可以处理多元回归；参数 na.action=na.omit 表示模型会丢弃包含缺失值的记录：

1
2
3
house_lm <- lm(AdjSalePrice ~ SqFtTotLiving + SqFtLot + Bathrooms +
Bedrooms + BldgGrade,
data=house, na.action=na.omit)

scikit-learn 的 LinearRegression 也可以用于多元线性回归：

1
2
3
4
predictors = ['SqFtTotLiving', 'SqFtLot', 'Bathrooms', 'Bedrooms', 'BldgGrade']
outcome = 'AdjSalePrice'
house_lm = LinearRegression()
house_lm.fit(house[predictors], house[outcome])

在 R 中打印 house_lm 对象会产生以下输出：

1
2
3
4
5
6
7
8
9
Call:
lm(formula = AdjSalePrice ~ SqFtTotLiving + SqFtLot + Bathrooms +
Bedrooms + BldgGrade, data = house, na.action = na.omit)

Coefficients:
(Intercept) SqFtTotLiving SqFtLot Bathrooms
-5.219e+05 2.288e+02 -6.047e-02 -1.944e+04
Bedrooms BldgGrade
-4.777e+04 1.061e+05

在 scikit-learn 的 LinearRegression 模型中，截距（intercept）和系数（coefficients）分别存储在拟合模型的 intercept_ 和 coef_ 属性中：

1
2
3
4
print(f'Intercept: {house_lm.intercept_:.3f}')
print('Coefficients:')
for name, coef in zip(predictors, house_lm.coef_):
    print(f' {name}: {coef}')

这些系数的解释与简单线性回归相同：在其他变量 \(X_k\)（当 \(k \neq j\)）保持不变的情况下，预测值 \(Y\) 每当 \(X_j\) 变化 1 个单位时，便按系数 \(b_j\) 的大小变化。例如，在房屋中增加一平方英尺的可用面积，估计价值大约增加 229 美元；增加 1,000 平方英尺的可用面积则意味着价值增加约 228,800 美元。

评估模型

Assessing the Model

从数据科学角度来看，最重要的性能指标是均方根误差（Root Mean Squared Error, RMSE）。RMSE 是预测值 \(\hat y_i\) 与真实值 \(y_i\) 的误差平方的平均值再开方： \[ \text{RMSE}=\sqrt{\frac{\sum_{i=1}^{n}(y_i-\hat y_i)^2}{n}} \]

它衡量模型的整体精度，也是将该模型与其他模型（包括用机器学习方法拟合的模型）进行比较的基础。与 RMSE 类似的是残差标准误差（Residual Standard Error, RSE）。在这种情况下有 \(p\) 个自变量，RSE 公式为：

\[ \text{RSE}=\sqrt{\frac{\sum_{i=1}^{n}(y_i-\hat y_i)^2}{n-p-1}} \]

唯一的区别在于分母——RSE 用自由度而不是样本数（参见本书第116页“自由度”部分）。在实践中，对于线性回归，RMSE 与 RSE 的差别通常非常小，尤其是在大数据场景下。

R 语言的 summary 函数可以计算 RSE 以及回归模型的其他指标：

1
summary(house_lm)

输出如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Call:
lm(formula = AdjSalePrice ~ SqFtTotLiving + SqFtLot + Bathrooms +
Bedrooms + BldgGrade, data = house, na.action = na.omit)

Residuals:
    Min       1Q   Median       3Q      Max
-1199479 -118908  -20977   87435  9473035

Coefficients:
               Estimate  Std. Error  t value  Pr(>|t|)
(Intercept)    -5.219e+05  1.565e+04 -33.342  < 2e-16 ***
SqFtTotLiving   2.288e+02  3.899e+00  58.694  < 2e-16 ***
SqFtLot        -6.047e-02  6.118e-02  -0.988   0.323
Bathrooms      -1.944e+04  3.625e+03  -5.363  8.27e-08 ***
Bedrooms       -4.777e+04  2.490e+03 -19.187  < 2e-16 ***
BldgGrade       1.061e+05  2.396e+03  44.277  < 2e-16 ***

---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 261300 on 22681 degrees of freedom
Multiple R-squared: 0.5406, Adjusted R-squared: 0.5405
F-statistic: 5338 on 5 and 22681 DF, p-value: < 2.2e-16

scikit-learn 提供了许多用于回归和分类的评估指标。这里我们用 mean_squared_error 计算 RMSE，用 r2_score 计算决定系数（R²）：

1
2
3
4
5
fitted = house_lm.predict(house[predictors])
RMSE = np.sqrt(mean_squared_error(house[outcome], fitted))
r2 = r2_score(house[outcome], fitted)
print(f'RMSE: {RMSE:.0f}')
print(f'r2: {r2:.4f}')

在 Python 中可以使用 statsmodels 对回归模型做更详细的分析：

1
2
3
model = sm.OLS(house[outcome], house[predictors].assign(const=1))
results = model.fit()
results.summary()

这里用到的 pandas 方法 assign 会在自变量中添加一个值为 1 的常数列，这是为了在模型中包含截距项所必需的。

另一个有用的指标：决定系数（R²）：你在软件输出中还会看到另一个有用的指标：决定系数（coefficient of determination），也叫 R² 统计量或 R-squared。R² 的取值范围从 0 到 1，用于衡量模型解释了数据变异的比例。它主要用于回归的解释性分析中，用来评估模型对数据的拟合程度。R² 的公式是： \[ R^2 = 1 - \frac{\sum_{i=1}^n (y_i-\hat{y}_i)^2}{\sum_{i=1}^n (y_i-\bar{y})^2} \]

分母与 \(Y\) 的方差成比例。R 的输出中还报告了 调整后的 R²（adjusted R-squared），它会根据自由度进行调整，相当于对模型中增加的预测变量进行惩罚。在大数据集的多元回归中，调整后的 R² 与普通 R² 差别通常不大。

在估计系数的同时，R 和 statsmodels 还会报告系数的标准误差（SE）以及 t 统计量：

\[ t_b=\frac{b}{SE(b)} \]

t 统计量（以及其对应的 p 值）衡量系数在统计意义上是否显著——也就是它是否超出了预测变量和目标变量之间随机关系所能产生的范围。 t 统计量越高（p 值越低），该预测变量的重要性就越显著。由于“简约”是模型的重要特征，因此像 t 统计量这样的工具非常有用，可以用来指导是否在模型中保留某个预测变量（参见第156页“模型选择与逐步回归”）。

警告

除了 t 统计量，R 和其他软件包通常还会报告 p 值（在 R 输出中为 Pr(>|t|)）以及 F 统计量。数据科学家通常不会深入解释这些统计量或“统计显著性”问题，而是主要把 t 统计量作为一个有用的参考：

  • 高 t 统计量（p 值接近 0） → 该预测变量应保留在模型中
  • 非常低的 t 统计量 → 该预测变量可以考虑移除 关于 p 值的更多讨论，见第106页“p 值”。

交叉验证

Cross-Validation

经典的统计回归指标（R²、F 统计量和 p 值）都是“样本内”指标（in-sample metrics）——也就是应用于用于拟合模型的同一批数据。直觉上，你可以看出，留出部分原始数据，不用它来拟合模型，再将模型应用于这部分留出样本（holdout sample）来测试其表现，会更有意义。通常，你会用大部分数据来训练模型，用一小部分来测试模型。

这种“样本外”验证（out-of-sample validation）的思路并不新鲜，但直到大数据集更普遍出现后才真正流行起来；在小数据集下，分析人员通常希望用到全部数据以拟合出最优模型。

然而，使用单个留出样本会引入不确定性：如果你选择了不同的留出样本，评估结果会有多大差别？

交叉验证将留出样本的思路扩展为多个连续的留出样本。基本 k 折交叉验证（k-fold cross-validation）的算法如下：

  1. 把数据中的 \(1/k\) 留作测试样本（holdout sample）。
  2. 用剩余的 \(k-1\) 份数据训练模型。
  3. 用模型对这 \(1/k\) 的留出样本进行预测，记录所需的模型评估指标。
  4. 把第一个 \(1/k\) 的数据放回，换取下一个 \(1/k\)（不包括已抽取过的记录）。
  5. 重复步骤 2 和 3。
  6. 持续重复，直到每条记录都曾被用作留出样本。
  7. 对所有折叠的评估指标进行平均或合并。

这种把数据分成训练集（training sample）和留出集（training sample）的划分方式，也称为一个折叠（fold）。

模型选择与逐步回归

Model Selection and Stepwise Regression

在某些问题中，回归模型可能有许多可用作预测变量的特征。例如，为了预测房屋价格，我们可以添加地下室面积、建造年份等额外变量。在 R 中，这些变量很容易添加到回归方程里：

1
2
3
4
5
house_full <- lm(AdjSalePrice ~ SqFtTotLiving + SqFtLot + Bathrooms +
Bedrooms + BldgGrade + PropertyType + NbrLivingUnits +
SqFtFinBasement + YrBuilt + YrRenovated +
NewConstruction,
data=house, na.action=na.omit)

在 Python 中，我们需要先把类别型和布尔型变量转换为数值：

1
2
3
4
5
6
7
8
predictors = ['SqFtTotLiving', 'SqFtLot', 'Bathrooms', 'Bedrooms', 'BldgGrade',
'PropertyType', 'NbrLivingUnits', 'SqFtFinBasement', 'YrBuilt',
'YrRenovated', 'NewConstruction']
X = pd.get_dummies(house[predictors], drop_first=True)
X['NewConstruction'] = [1 if nc else 0 for nc in X['NewConstruction']]
house_full = sm.OLS(house[outcome], X.assign(const=1))
results = house_full.fit()
results.summary()

然而，添加更多变量并不一定意味着我们得到了更好的模型。统计学家遵循奥卡姆剃刀原则（Occam’s razor）来指导模型选择：在其他条件相同的情况下，应该优先使用更简单的模型，而不是更复杂的模型。

在训练数据中，增加变量总是会降低 RMSE 并提高 R²，因此这些指标并不能很好地指导模型选择。一种把模型复杂度纳入考虑的方法是使用调整后的 R²：

\[ R^2_{\text{adj}} = 1 - (1-R^2)\frac{n-1}{n-P-1} \]

其中 \(n\) 是样本数，\(P\) 是模型中的变量数。

警告:

AIC、BIC 和 Mallows Cp：20世纪70年代，日本著名统计学家赤池弘次（Hirotugu Akaike）提出了一个指标 AIC（Akaike 信息准则，Akaike’s Information Criteria），它会对模型中新增的变量进行惩罚。对于回归模型，AIC 公式为： \[ AIC = 2P + n\log\left(\frac{RSS}{n}\right) \]

其中 \(P\) 是变量数，\(n\) 是样本数。目标是找到使 AIC 最小的模型；如果多加了 \(k\) 个变量，模型会受到 \(2k\) 的惩罚。

AIC 有一些常见变体：

  • AICc：AIC 在小样本情况下的修正版本。
  • BIC（Bayesian information criteria，贝叶斯信息准则）：类似 AIC，但对新增变量的惩罚更强。
  • Mallows Cp：Colin Mallows 提出的 AIC 变体。

这些指标通常在训练集（样本内）上报告；如果数据科学家使用留出样本（holdout data）来评估模型，就不必过于担心这些指标之间的差异或其背后的理论。

如何找到最小 AIC 或最大调整后 R² 的模型呢？一种方法是搜索所有可能的模型，称为全子集回归（all subset regression）。这种方法计算量很大，对于包含大量数据和变量的问题来说不可行。一个更有吸引力的替代方法是使用逐步回归（stepwise regression）。

  • 可以从完整模型开始，逐步去掉没有显著贡献的变量（称为后向消除 backward elimination）。
  • 也可以从常数模型开始，逐步加入变量（前向选择 forward selection）。
  • 还可以交替加入和移除预测变量，以找到能降低 AIC 或调整后 R² 的模型。

R 中 Venables 和 Ripley 提供的 MASS 包就有一个逐步回归函数 stepAIC：

1
2
3
library(MASS)
step <- stepAIC(house_full, direction="both")
step

示例输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Call:
lm(formula = AdjSalePrice ~ SqFtTotLiving + Bathrooms + Bedrooms +
BldgGrade + PropertyType + SqFtFinBasement + YrBuilt, data = house,
na.action = na.omit)

Coefficients:
(Intercept)            SqFtTotLiving
6.179e+06              1.993e+02
Bathrooms              Bedrooms
4.240e+04             -5.195e+04
BldgGrade              PropertyTypeSingle Family
1.372e+05              2.291e+04
PropertyTypeTownhouse  SqFtFinBasement
8.448e+04              7.047e+00
YrBuilt
-3.565e+03

​

个人注：以下是用gemini翻译 20250915 12:00

scikit-learn 没有实现逐步回归的功能。我们在我们的 dmba 包中实现了 stepwise_selection、forward_selection 和 backward_elimination 函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
y = house[outcome]
def train_model(variables):
    if len(variables) == 0:
        return None
    model = LinearRegression()
    model.fit(X[variables], y)
    return model
def score_model(model, variables):
    if len(variables) == 0:
        return AIC_score(y, [y.mean()] * len(y), model, df=1)
    return AIC_score(y, model.predict(X[variables]), model)
best_model, best_variables = stepwise_selection(X.columns, train_model, score_model, verbose=True)
print(f'Intercept: {best_model.intercept_:.3f}')
print('Coefficients:')
for name, coef in zip(best_variables, best_model.coef_):
    print(f' {name}: {coef}')

定义一个函数，该函数为一组给定的变量返回一个拟合好的模型。定义一个函数，该函数为给定的模型和一组变量返回一个得分。在本例中，我们使用了 dmba 包中实现的 AIC_score。该函数选择了一个模型，其中 house_full 中的几个变量被剔除：SqFtLot、NbrLivingUnits、YrRenovated 和 NewConstruction。

更简单的方法是前向选择和后向选择。在前向选择中，你从零个预测变量开始，然后逐一添加，每一步都添加对 \(R^2\) 贡献最大的预测变量，当贡献不再具有统计显著性时停止。在后向选择，或者说后向消除中，你从完整模型开始，然后移除不具有统计显著性的预测变量，直到你剩下的模型中所有预测变量都具有统计显著性。

惩罚回归在精神上与 AIC 相似。它不是通过显式地搜索离散的模型集合，而是在模型拟合方程中加入一个惩罚，对拥有太多变量（参数）的模型进行惩罚。惩罚回归不会像逐步、前向和后向选择那样完全消除预测变量，而是通过减少系数来应用惩罚，在某些情况下会使其接近于零。常见的惩罚回归方法是岭回归（ridge regression）和 Lasso 回归（lasso regression）。

逐步回归和所有子集回归都是样本内方法，用于评估和调整模型。这意味着模型选择可能存在过拟合（拟合数据中的噪声），并且在应用于新数据时性能可能不佳。避免这种情况的一种常见方法是使用交叉验证来验证模型。在线性回归中，过拟合通常不是一个主要问题，因为数据被强加了一个简单的（线性）全局结构。对于更复杂的模型类型，特别是那些对局部数据结构作出反应的迭代过程，交叉验证是一个非常重要的工具；详见第155页的“交叉验证”部分。

加权回归

Weighted Regression

统计学家出于多种目的使用加权回归；尤其是在分析复杂调查数据时，它非常重要。数据科学家可能会在以下两种情况下发现加权回归很有用：

  1. 逆方差加权：当不同观测值的测量精度不同时，可以采用这种方法；方差较高的观测值权重较低。
  2. 多案例数据分析：当数据中的每一行代表多个原始观测值时，权重变量编码了每行所代表的原始观测值数量。

以住房数据为例，较早的销售数据通常不如最近的销售数据可靠。我们可以使用 DocumentDate 来确定销售年份，并计算一个 Weight 变量，该变量是自2005年（数据开始年份）以来的年数：

1
2
3
library(lubridate)
house$Year = year(house$DocumentDate)
house$Weight = house$Year - 2005
1
2
house['Year'] = [int(date.split('-')[0]) for date in house.DocumentDate]
house['Weight'] = house.Year - 2005

我们可以使用 lm 函数中的 weight 参数计算加权回归：

1
2
3
4
5
house_wt <- lm(AdjSalePrice ~ SqFtTotLiving + SqFtLot + Bathrooms +
Bedrooms + BldgGrade,
data=house, weight=Weight)
round(cbind(house_lm=house_lm$coefficients,
house_wt=house_wt$coefficients), digits=3)
house_lm house_wt
(Intercept) -521871.368 -584189.329
SqFtTotLiving 228.831 245.024
SqFtLot -0.060 -0.292
Bathrooms -19442.840 -26085.970
Bedrooms -47769.955 -53608.876
BldgGrade 106106.963 115242.435

加权回归中的系数与原始回归中的系数略有不同。

scikit-learn 中的大多数模型在其 fit 方法调用中都接受 sample_weight 作为关键字参数：

1
2
3
4
predictors = ['SqFtTotLiving', 'SqFtLot', 'Bathrooms', 'Bedrooms', 'BldgGrade']
outcome = 'AdjSalePrice'
house_wt = LinearRegression()
house_wt.fit(house[predictors], house[outcome], sample_weight=house.Weight)

关键思想

  • 多元线性回归：对响应变量 Y 与多个预测变量 X1, ..., Xp 之间的关系进行建模。
  • 最重要的评估指标：评估模型的最重要指标是均方根误差 (RMSE) 和 R平方 (\(R^2\))。
  • 系数的标准误：可用于衡量变量对模型贡献的可靠性。
  • 逐步回归：一种自动确定哪些变量应包含在模型中的方法。
  • 加权回归：用于在方程拟合过程中给予某些记录更多或更少的权重。

使用回归进行预测

Prediction Using Regression

在数据科学中，回归的主要目的是预测。这一点值得我们牢记，因为回归作为一种古老且成熟的统计方法，附带了一些与其作为解释性建模工具的传统角色更相关的“包袱（baggage）”，而这些包袱与预测的目的关系不大。

使用回归进行预测的关键术语

  • 预测区间（Prediction interval） 围绕单个预测值的不确定性区间。
  • 外推法（Extrapolation） 将模型扩展到用于拟合它的数据范围之外。

外推的危险性

The Dangers of Extrapolation

回归模型不应该被用来进行外推，即预测超出其训练数据范围之外的值（不包括将回归用于时间序列预测的情况）。模型仅对那些数据中存在足够值的预测变量值有效（即使有足够的数据，也可能存在其他问题，详见第176页的“回归诊断”）。

举一个极端的例子，假设我们使用 model_lm 来预测一块5000平方英尺空地的价值。在这种情况下，所有与建筑物相关的预测变量值都将为0，而回归方程将得出一个荒谬的预测值：-521,900 + 5,000 × -0.0605 = -$522,202。为什么会发生这种情况？因为我们的数据只包含带有建筑物的地块，没有任何对应空地的记录。因此，模型没有任何信息来告诉它如何预测空地的销售价格。

置信区间与预测区间

Confidence and Prediction Intervals

统计学的大部分内容都涉及理解和衡量变异性（不确定性）。回归输出中报告的 t 统计量和 p 值以一种正式的方式处理了这个问题，这有时对于变量选择是有用的（详见第153页的“评估模型”）。更有用的指标是置信区间，它是不确定性区间，围绕着回归系数和预测值。理解这一点的一个简单方法是通过自助法（bootstrap）（关于一般的自助法程序，详见第61页）。在软件输出中最常见的回归置信区间是针对回归参数（系数）的。

以下是为具有P个预测变量和n个记录（行）的数据集生成回归参数（系数）置信区间的自助法算法：

  1. 将每一行（包括结果变量）视为一张单独的“票据”，并将所有n张票据放入一个盒子里。
  2. 随机抽取一张票据，记录下值，然后将其放回盒中。
  3. 重复步骤2共n次；你现在有了一个自助法重抽样样本。
  4. 对这个自助法样本进行回归拟合，并记录估计的系数。
  5. 重复步骤2到步骤4，例如1000次。
  6. 现在你拥有了每个系数的1000个自助法值；找到每个值的相应百分位数（例如，90%置信区间的第5和第95百分位数）。

在 R 语言中，你可以使用 Boot 函数来生成实际的自助法置信区间，或者简单地使用 R 的常规输出中基于公式的区间。它们的概念含义和解释是相同的，并且对数据科学家来说不那么重要，因为它们关注的是回归系数。

对数据科学家来说，更重要的是围绕预测 y 值（\(Y_i\)）的区间。围绕 \(Y_i\) 的不确定性来自两个来源：

  • 不确定性（Uncertainty）：关于相关的预测变量及其系数是什么（参考前面的自助法算法）。
  • 附加误差（Additional error）：个体数据点固有的附加误差。

个体数据点误差可以这样理解：即使我们确切知道回归方程是什么（例如，如果我们有海量的记录来拟合它），对于一组给定的预测变量值，实际的结果值仍然会存在差异。例如，几栋房子——每栋都有8个房间、6500平方英尺的土地、3个浴室和一个地下室——它们的价值可能不同。我们可以用拟合值中的残差（residuals）来模拟这种个体误差（individual error）。

用于同时模拟回归模型误差和个体数据点误差的自助法算法如下所示：

  1. 从数据中抽取一个自助法样本（前面已详细说明）。
  2. 拟合回归模型，并预测新值。
  3. 从原始回归拟合中随机抽取一个残差，将其加到预测值上，并记录结果。
  4. 重复步骤1到3，例如1000次。
  5. 找到结果的2.5%和97.5%百分位数。

个人注：第 3 步（随机抽取残差加到预测值上）的例子

1、 假设我们有这样一个回归模型

我们用房屋面积预测房价（单位：美元）：

面积 (X) 真实价格 (Y)
1000 200,000
1500 250,000
2000 280,000

我们拟合出一个简单回归：

\[ \hat Y = 100000 + 90 X \]

这样预测值和残差分别是：

X 真实 Y 预测 \(\hat Y\) 残差 \(r=Y-\hat Y\)
1000 200000 190000 +10000
1500 250000 235000 +15000
2000 280000 280000 0

2、 我们要预测一个新房屋

面积 1800 平方英尺。模型预测值：

\[ \hat Y_\text{new} = 100000 + 90*1800 = 262000 \]

但是我们知道模型有误差，于是用 bootstrap 残差来模拟。

3、 第 3 步：随机抽取一个残差，加到预测值上

  • 我们有原始残差集合 \(\{+10000, +15000, 0\}\)
  • 假设第一次随机抽到 +15000
  • 那么新的“模拟观测值”就是

\[ 262000 + 15000 = 277000 \]

下一次 bootstrap 可能抽到残差 0，那么就是

\[ 262000 + 0 = 262000 \]

再下一次抽到残差 +10000，就是

\[ 262000 + 10000 = 272000 \]

4、 重复多次

我们重复这个过程（步骤1–3）1000次，就能得到 262000、272000、277000… 这样一堆“预测+误差”的值。

把这些值排序，取第2.5百分位和第97.5百分位，就得到了这个新房屋价格预测的95%预测区间。

5、 总结 第3步的“随机取残差加回预测值”就是用模型拟合后的残差来“模拟”未来观测的随机误差，让你不仅有一个点预测值，还有一个预测区间。

关键思想

  • 外推：超出数据范围的预测可能导致错误。
  • 置信区间：量化围绕回归系数的不确定性。
  • 预测区间：量化个体预测值的不确定性。
  • 软件输出：包括 R 在内的大多数软件都会使用公式生成预测和置信区间，作为默认或指定的输出。
  • 自助法：也可以用于生成预测和置信区间；其解释和思想是相同的。

警告：

预测区间还是置信区间？预测区间（prediction interval）与单个值的不确定性有关，而置信区间（confidence interval）与从多个值计算得出的均值或其他统计量有关。因此，预测区间通常会比相同值的置信区间宽得多。我们在自助法模型中通过选择一个单独的残差并将其附加到预测值上来模拟这种个体值误差。你应该使用哪一个？这取决于分析的背景和目的，但总的来说，数据科学家对特定的个体预测更感兴趣，因此预测区间会更合适。当你应该使用预测区间时却使用了置信区间，将大大低估给定预测值中的不确定性。

回归中的因子变量

Factor Variables in Regression

因子变量，也称为分类变量（categorical variables），取有限数量的离散值。例如，贷款用途可以是“债务整合”、“婚礼”、“汽车”等等。二元（binary）（是/否）变量，也叫指示变量（indicator variabl），是因子变量的一种特殊情况。

回归模型需要数值输入，因此因子变量需要重新编码才能在模型中使用。最常见的方法是将一个因子变量转换为一组二元虚拟变量（binary dummy variables）。

因子变量的关键术语

  • 虚拟变量（Dummy variables） 由重新编码因子数据而来的二元 0-1 变量，用于回归和其他模型。

  • 参考编码（Reference coding） 统计学家最常用的编码类型，其中一个因子水平被用作参考，其他因子水平与该参考水平进行比较。 同义词：处理编码（treatment coding）

  • 独热编码（One hot encoder） 机器学习社区常用的一种编码类型，其中所有因子水平都被保留。虽然对某些机器学习算法很有用，但这种方法不适用于多元线性回归。

  • 偏差编码（Deviation coding） 一种将每个水平与整体均值进行比较，而不是与参考水平进行比较的编码类型。 同义词：总和对比（sum contrasts）

虚拟变量表示

Dummy Variables Representation

在金县住房数据中，有一个用于表示房产类型的因子变量；下面是其中六条记录的一个小样本：

1
2
3
4
5
6
7
8
9
10
head(house[, 'PropertyType'])
Source: local data frame [6 x 1]
  PropertyType
        (fctr)
1  Multiplex
2  Single Family
3  Single Family
4  Single Family
5  Single Family
6  Townhouse
1
house.PropertyType.head()

该变量有三个可能的值：Multiplex（多户住宅）、Single Family（独栋住宅）和 Townhouse（联排别墅）。为了使用这个因子变量，我们需要将其转换成一组二元变量。我们通过为因子变量的每个可能值创建一个二元变量来实现。在 R 语言中，我们使用 model.matrix 函数来完成此操作：

1
2
3
4
5
6
7
8
9
prop_type_dummies <- model.matrix(~PropertyType -1, data=house)
head(prop_type_dummies)
  PropertyTypeMultiplex PropertyTypeSingle Family PropertyTypeTownhouse
1                     1                      0                     0
2                     0                      1                     0
3                     0                      1                     0
4                     0                      1                     0
5                     0                      1                     0
6                     0                      0                     1

model.matrix 函数将数据框转换为适合线性模型的矩阵。具有三个不同水平的因子变量 PropertyType 被表示为一个三列的矩阵。在机器学习社区中，这种表示被称为独热编码（见第242页的“独热编码”）。

在 Python 中，我们可以使用 pandas 的 get_dummies 方法将分类变量转换为虚拟变量：

1
2
pd.get_dummies(house['PropertyType']).head()
pd.get_dummies(house['PropertyType'], drop_first=True).head()

默认情况下，该函数返回分类变量的独热编码。关键字参数 drop_first 将返回 P-1 列。使用这个参数可以避免多重共线性问题。在某些机器学习算法中，例如最近邻算法和树模型，独热编码是表示因子变量的标准方法（例如，参见第249页的“树模型”）。

在回归设置中，一个具有 \(P\) 个不同水平的因子变量通常只用一个具有 \(P-1\) 列的矩阵来表示。这是因为回归模型通常包含一个截距项。有了截距项，一旦你定义了 \(P-1\) 个二元变量的值，第 \(P\) 个的值就已知了，可以被认为是多余的。添加第 \(P\) 列会导致多重共线性错误（详见第172页的“多重共线性”）。

参考编码：R 中的默认表示方法是使用第一个因子水平作为参考水平，并解释其他水平相对于该水平的差异。

1
2
lm(AdjSalePrice ~ SqFtTotLiving + SqFtLot + Bathrooms +
Bedrooms + BldgGrade + PropertyType, data=house)

输出结果：

1
2
3
4
5
6
7
8
9
Coefficients:
(Intercept) SqFtTotLiving
-4.468e+05 2.234e+02
SqFtLot Bathrooms
-7.037e-02 -1.598e+04
Bedrooms BldgGrade
-5.089e+04 1.094e+05
PropertyTypeSingle Family PropertyTypeTownhouse
-8.468e+04 -1.151e+05

get_dummies 方法接受一个可选的关键字参数 drop_first，用来排除第一个因子作为参考：

1
2
3
4
5
6
7
8
9
predictors = ['SqFtTotLiving', 'SqFtLot', 'Bathrooms', 'Bedrooms',
'BldgGrade', 'PropertyType']
X = pd.get_dummies(house[predictors], drop_first=True)
house_lm_factor = LinearRegression()
house_lm_factor.fit(X, house[outcome])
print(f'Intercept: {house_lm_factor.intercept_:.3f}')
print('Coefficients:')
for name, coef in zip(X.columns, house_lm_factor.coef_):
    print(f' {name}: {coef}')

R 回归的输出结果显示了两个与 PropertyType 对应的系数：PropertyTypeSingle Family 和 PropertyTypeTownhouse。由于当 PropertyTypeSingle Family == 0 且 PropertyTypeTownhouse == 0 时，Multiplex 的值被隐式定义，因此没有 Multiplex 的系数。这些系数被解释为相对于 Multiplex 的相对值，因此，一个独栋家庭住宅（Single Family）的价值比多户住宅（Multiplex）低近 $85,000，而一个联排别墅（Townhouse）的价值则低超过 $150,000。

警告

不同的因子编码方式：有几种不同的编码因子变量的方法，统称为对比编码系统（contrast coding systems）。例如，偏差编码（deviation coding），也称为总和对比（sum contrasts），将每个水平与整体均值进行比较。另一种对比是多项式编码（polynomial coding），它适用于有序因子；详见第169页的“有序因子变量”部分。除了有序因子之外，数据科学家通常不会遇到除了参考编码或独热编码**之外的任何其他编码类型。

具有许多水平的因子变量

Factor Variables with Many Levels

有些因子变量可能会产生大量的二元虚拟变量，例如邮政编码就是一个因子变量，而美国有43,000个邮政编码。在这种情况下，有必要探索数据以及预测变量和结果之间的关系，以确定这些类别中是否包含有用的信息。如果包含，你还必须决定是保留所有因子水平，还是应该进行合并。

在金县（King County）的住房数据中，有80个邮政编码有房屋销售记录：

1
table(house$ZipCode)
98001 98002 ... 98199 98224 98288 98354
358 180 ... 393 3 4 9

pandas 数据框的 value_counts 方法返回相同的信息：

1
pd.DataFrame(house['ZipCode'].value_counts()).transpose()

邮政编码是一个重要的变量，因为它代表了位置对房屋价值的影响。包含所有水平需要79个系数，对应79个自由度。原始模型 house_lm 只有5个自由度；参见第153页的“评估模型”。此外，有几个邮政编码只有一次销售记录。在某些问题中，你可以通过使用邮政编码的前两位或三位数字来合并它们，这对应于一个次级大都市地理区域。对于金县，几乎所有的销售都发生在 980xx 或 981xx，所以这种方法没有帮助。

另一种方法是根据另一个变量，如销售价格，对邮政编码进行分组。更好的方法是使用初始模型的残差来形成邮政编码组。以下 R 语言中的 dplyr 代码将80个邮政编码基于 house_lm 回归模型的残差中位数合并成五个组：

1
2
3
4
5
6
7
8
9
10
zip_groups <- house %>%
mutate(resid = residuals(house_lm)) %>%
group_by(ZipCode) %>%
summarize(med_resid = median(resid),
cnt = n()) %>%
arrange(med_resid) %>%
mutate(cum_cnt = cumsum(cnt),
ZipGroup = ntile(cum_cnt, 5))
house <- house %>%
left_join(select(zip_groups, ZipCode, ZipGroup), by='ZipCode')

为每个邮政编码计算残差中位数，然后使用 ntile 函数将按中位数排序的邮政编码分成五个组。有关如何将此作为回归项来改进原始拟合的示例，请参阅第172页的“混杂变量”。

在 Python 中，我们可以按如下方式计算此信息：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
zip_groups = pd.DataFrame([
    *pd.DataFrame({
        'ZipCode': house['ZipCode'],
        'residual' : house[outcome] - house_lm.predict(house[predictors]),
    })
    .groupby(['ZipCode'])
    .apply(lambda x: {
        'ZipCode': x.iloc[0,0],
        'count': len(x),
        'median_residual': x.residual.median()
    })
]).sort_values('median_residual')
zip_groups['cum_count'] = np.cumsum(zip_groups['count'])
zip_groups['ZipGroup'] = pd.qcut(zip_groups['cum_count'], 5, labels=False,
retbins=False)
to_join = zip_groups[['ZipCode', 'ZipGroup']].set_index('ZipCode')
house = house.join(to_join, on='ZipCode')
house['ZipGroup'] = house['ZipGroup'].astype('category')

利用残差来指导回归拟合的概念是建模过程中的一个基本步骤；详见第176页的“回归诊断”。

有序因子变量

Ordered Factor Variables

有些因子变量反映了因子的水平高低；这些变量被称为有序因子变量或有序分类变量。例如，贷款评级可以是A、B、C等——每个评级都比前一个评级风险更高。通常，有序因子变量可以直接转换为数值并使用。例如，BldgGrade（建筑等级）就是一个有序因子变量。表4-1中展示了几种等级类型。虽然这些等级有特定的含义，但其数值从低到高排列，对应着更高等级的住宅。在第150页“多元线性回归”中拟合的回归模型 house_lm 中，BldgGrade 被视为一个数值变量。

T4.1

将有序因子视为数值变量可以保留其包含的顺序信息，而如果将其转换为因子变量，这些信息就会丢失。

关键思想

  • 因子变量：需要转换为数值变量才能在回归模型中使用。
  • 编码方法：对一个具有 \(P\) 个不同值的因子变量进行编码最常用的方法是使用 \(P-1\) 个虚拟变量来表示。
  • 水平过多的因子变量：即使在非常大的数据集中，具有许多水平的因子变量也可能需要合并为具有较少水平的变量。
  • 有序因子：某些因子的水平是有序的，可以表示为一个单独的数值变量。

解释回归方程

Interpreting the Regression Equation

在数据科学中，回归最主要的应用是预测某个因变量（结果变量）。然而，在某些情况下，从方程本身获得洞见以理解预测变量和结果之间的关系本质也很有价值。本节提供了关于如何检查和解释回归方程的指导。

解释回归方程的关键术语

  • 相关变量（Correlated variables） 当预测变量高度相关时，很难解释单个系数。

  • 多重共线性（Multicollinearity） 当预测变量之间存在完全或接近完全的相关性时，回归可能不稳定或无法计算。 同义词：共线性（collinearity）

  • 混杂变量（Confounding variables） 一个重要的预测变量，当被遗漏时，会导致回归方程中出现虚假关系。

  • 主效应（Main effects） 一个预测变量与结果变量之间的关系，独立于其他变量。

  • 交互作用（Interactions） 两个或多个预测变量与响应变量之间的相互依存关系。

相关预测变量

Correlated Predictors

在多元回归中，预测变量通常彼此之间存在相关性。举个例子，我们可以检查在第156页“模型选择与逐步回归”中拟合的模型 step_lm 的回归系数。

1
2
3
4
5
6
7
step_lm$coefficients
(Intercept) SqFtTotLiving       Bathrooms
 6.178645e+06  1.992776e+02    4.239616e+04
     Bedrooms     BldgGrade PropertyTypeSingle Family
 -5.194738e+04  1.371596e+05    2.291206e+04
PropertyTypeTownhouse SqFtFinBasement         YrBuilt
  8.447916e+04    7.046975e+00   -3.565425e+03
1
2
3
4
print(f'Intercept: {best_model.intercept_:.3f}')
print('Coefficients:')
for name, coef in zip(best_variables, best_model.coef_):
    print(f' {name}: {coef}')

Bedrooms 的系数是负数！这暗示着给一栋房子增加一间卧室会降低其价值。这怎么可能呢？这是因为预测变量之间是相关的：更大的房子往往有更多的卧室，而真正驱动房屋价值的是面积，而不是卧室的数量。你可以这样理解：考虑两栋面积完全相同的房子，我们有理由认为卧室更多但更小的那栋房子会不那么受欢迎。

拥有相关联的预测变量会使解释回归系数的符号和值变得困难（并且可能夸大估计值的标准误）。卧室数量、房屋面积和浴室数量这几个变量都是相互关联的。以下面的 R 语言示例为例，它拟合了一个新的回归模型，从方程中移除了 SqFtTotLiving、SqFtFinBasement 和 Bathrooms 变量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
update(step_lm, .
~
.
- SqFtTotLiving - SqFtFinBasement - Bathrooms)
Call:
lm(formula = AdjSalePrice ~ Bedrooms + BldgGrade + PropertyType +
YrBuilt, data = house, na.action = na.omit)
Coefficients:
      (Intercept)         Bedrooms
          4913973          27151
        BldgGrade PropertyTypeSingle Family
           248998         -19898
PropertyTypeTownhouse         YrBuilt
        -47355         -3212

update 函数可用于从模型中添加或移除变量。现在，Bedrooms 的系数变为正数——这与我们的预期相符（尽管在移除了房屋面积等变量后，它实际上充当了房屋大小的替代变量）。

在 Python 中，没有与 R 的 update 函数等效的功能。我们需要使用修改后的预测变量列表重新拟合模型：

1
2
3
4
5
predictors = ['Bedrooms', 'BldgGrade', 'PropertyType', 'YrBuilt']
outcome = 'AdjSalePrice'
X = pd.get_dummies(house[predictors], drop_first=True)
reduced_lm = LinearRegression()
reduced_lm.fit(X, house[outcome])

相关变量只是解释回归系数的一个问题。在 house_lm 模型中，没有变量来解释房屋的位置，这个模型将非常不同的区域类型混在一起。位置可能是一个混杂变量；更多讨论请参见第172页的“混杂变量”。

多重共线性

Multicollinearity

多重共线性是由相关变量所引发的极端情况——预测变量之间存在冗余。当一个预测变量可以表示为其他预测变量的线性组合时，就会出现完全多重共线性。

多重共线性通常发生在以下情况：

  • 重复包含：一个变量被错误地包含了多次。
  • 不当的虚拟变量：由一个因子变量创建了 \(P\) 个虚拟变量，而不是正确的 \(P-1\) 个（参见第163页的“回归中的因子变量”）。
  • 高度相关：两个变量几乎是完全相关的。

在回归分析中，必须处理多重共线性——应该移除变量直到多重共线性消失。在存在完全多重共线性的情况下，回归模型没有明确定义的解。许多软件，包括 R 和 Python，会自动处理某些类型的多重共线性。例如，如果在房屋数据回归中两次包含 SqFtTotLiving 变量，其结果与 house_lm 模型的结果相同。在非完全多重共线性的情况下，软件可能会得到一个解，但结果可能不稳定。

通用注解

对于非线性回归方法，如树模型、聚类和最近邻算法，多重共线性不是一个大问题，在这些方法中保留全部 \(P\) 个虚拟变量（而不是 \(P-1\) 个）可能是可取的。即便如此，在这些方法中，预测变量的非冗余性仍然是一种优点。

混杂变量

Confounding Variables

相关变量的问题在于加入了太多相似的变量，而混杂变量的问题在于遗漏了重要的变量。如果对回归方程的系数进行天真的解释，可能会得出无效的结论。

以第151页“示例：金县住房数据”中的金县回归方程 house_lm 为例。SqFtLot、Bathrooms 和 Bedrooms 的回归系数都是负的。这个原始回归模型没有包含代表位置的变量——而位置是房屋价格的一个非常重要的预测因子。

为了对位置进行建模，我们引入一个ZipGroup变量，它将邮政编码分为五组，从最便宜（1）到最贵（5）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
lm(formula = AdjSalePrice ~ SqFtTotLiving + SqFtLot + Bathrooms +
Bedrooms + BldgGrade + PropertyType + ZipGroup, data = house,
na.action = na.omit)
Coefficients:
      (Intercept)   SqFtTotLiving
       -6.666e+05    2.106e+02
        SqFtLot       Bathrooms
        4.550e-01    5.928e+03
       Bedrooms       BldgGrade
      -4.168e+04    9.854e+04
PropertyTypeSingle Family PropertyTypeTownhouse
       1.932e+04    -7.820e+04
         ZipGroup2      ZipGroup3
        5.332e+04    1.163e+05
         ZipGroup4      ZipGroup5
        1.784e+05    3.384e+05

Python 中相同的模型：

1
2
3
4
5
6
7
8
9
10
predictors = ['SqFtTotLiving', 'SqFtLot', 'Bathrooms', 'Bedrooms',
'BldgGrade', 'PropertyType', 'ZipGroup']
outcome = 'AdjSalePrice'
X = pd.get_dummies(house[predictors], drop_first=True)
confounding_lm = LinearRegression()
confounding_lm.fit(X, house[outcome])
print(f'Intercept: {confounding_lm.intercept_:.3f}')
print('Coefficients:')
for name, coef in zip(X.columns, confounding_lm.coef_):
    print(f' {name}: {coef}')

ZipGroup 显然是一个重要的变量：位于最贵邮政编码组的房屋，其估计销售价格要高出近 $340,000。现在，SqFtLot 和 Bathrooms 的系数变为正数，增加一个浴室会使销售价格增加 $5,928。

Bedrooms 的系数仍然是负数。虽然这看起来不合直觉，但这在房地产领域是一个众所周知的现象。对于居住面积和浴室数量相同的房屋，卧室数量更多（因此卧室更小）的房屋通常与较低的价值相关联。

交互作用与主效应

Interactions and Main Effects

统计学家喜欢区分主效应（或称自变量 independent variables）和主效应之间的交互作用。主效应通常是指回归方程中的预测变量。当模型中只使用主效应时，一个隐含的假设是：预测变量与响应变量之间的关系是独立于其他预测变量的。然而，情况往往并非如此。

例如，在第172页“混杂变量”中拟合的金县住房数据模型包含了几个变量作为主效应，其中包括ZipCode。在房地产中，位置是决定一切的关键，因此很自然地会假设，房屋面积与销售价格之间的关系取决于位置。一个建在低租金区域的大房子，其价值不会与建在昂贵区域的大房子相同。在 R 中，你可以使用 * 运算符来包含变量之间的交互作用。对于金县数据，以下代码拟合了 SqFtTotLiving 和 ZipGroup 之间的交互作用：

1
2
3
lm(formula = AdjSalePrice ~ SqFtTotLiving * ZipGroup + SqFtLot +
Bathrooms + Bedrooms + BldgGrade + PropertyType, data = house,
na.action = na.omit)

输出结果：

1
2
Coefficients:
(Intercept) ... SqFtTotLiving:ZipGroup2 ...

得到的模型有四个新项：SqFtTotLiving:ZipGroup2、SqFtTotLiving:ZipGroup3 等等。

在 Python 中，我们需要使用 statsmodels 包来训练包含交互作用的线性回归模型。这个包的设计类似于 R，并允许使用公式接口来定义模型：

1
2
3
4
model = smf.ols(formula='AdjSalePrice ~ SqFtTotLiving*ZipGroup + SqFtLot + ' +
'Bathrooms + Bedrooms + BldgGrade + PropertyType', data=house)
results = model.fit()
results.summary()

statsmodels 包会自动处理分类变量（例如 ZipGroup[T.1]、PropertyType[T.Single Family]）和交互项（例如 SqFtTotLiving:ZipGroup[T.1]）。

位置和房屋面积似乎存在强烈的交互作用。对于最低 ZipGroup 中的房屋，其斜率与主效应 SqFtTotLiving 的斜率相同，即每平方英尺118美元（这是因为 R 对因子变量使用参考编码；参见第163页的“回归中的因子变量”）。对于最高 ZipGroup 中的房屋，斜率是主效应加上 SqFtTotLiving:ZipGroup5 的总和，即115美元 + 227美元 = 每平方英尺342美元。换句话说，与增加一平方英尺的平均价值提升相比，在最昂贵的邮政编码组中增加一平方英尺，其预测销售价格的提升因子几乎是三倍。

知识点

包含交互项的模型选择：在涉及许多变量的问题中，决定模型应包含哪些交互项可能具有挑战性。通常采取几种不同的方法：

  • 在某些问题中，先验知识和直觉可以指导选择要包含在模型中的交互项。
  • 可以使用逐步选择（参见第156页的“模型选择与逐步回归”）来筛选各种模型。
  • 惩罚回归可以自动拟合一大组可能的交互项。
  • 也许最常见的方法是使用树模型及其后代，如随机森林和梯度提升树。这类模型会自动搜索最佳的交互项；参见第249页的“树模型”。

关键思想

  • 相关预测变量：由于预测变量之间的相关性，在解释多元线性回归的系数时必须谨慎。
  • 多重共线性：可能导致回归方程拟合时的数值不稳定。
  • 混杂变量：一个被模型遗漏的重要预测变量，可能导致回归方程中出现虚假关系。
  • 交互项：如果变量与响应变量之间的关系是相互依存的，则需要引入两个变量之间的交互项。

回归诊断

Regression Diagnostics

在解释性建模（explanatory modeling）（即研究背景）中，除了前面提到的指标（参见第153页的“评估模型”）之外，还会采取各种步骤来评估模型对数据的拟合程度；这些步骤大多基于残差分析。它们不直接关乎预测准确性，但可以在预测场景中提供有用的洞见。

回归诊断的关键术语

  • 标准化残差（Standardized residuals） 残差除以残差的标准误。

  • 离群值（Outliers） 与数据其余部分（或预测结果）相距甚远的记录（或结果值）。

  • 影响力值（Influential value） 其存在或缺失对回归方程产生重大影响的值或记录。

  • 杠杆值（Leverage） 单个记录对回归方程影响的程度。 同义词：帽子值（hat-value）

  • 非正态残差（Non-normal residuals） 残差不呈正态分布会使回归的一些技术要求失效，但在数据科学中通常不是一个主要问题。

  • 异方差性（Heteroskedasticity） 当结果变量的某些范围内的残差具有更高的方差时（可能表明方程中缺少某个预测变量）。

  • 偏残差图（Partial residual plots） 一个诊断图，用于揭示结果变量与单个预测变量之间的关系。 同义词：增广变量图（added variables plot）

离群值

Outliers

一般来说，一个极端值，也称为离群值，是与大多数其他观测值相距甚远的值。正如在处理位置和变异性估计时需要处理离群值一样（参见第7页的“位置估计”和第13页的“变异性估计”），离群值也可能给回归模型带来问题。在回归中，离群值是指其实际 \(y\) 值与预测值相距甚远的记录。你可以通过检查标准化残差来检测离群值，标准化残差是将残差除以残差的标准误。

没有统计学理论可以区分离群值和非离群值。相反，有一些（任意的）经验法则来界定一个观测值需要与主体数据相距多远才能被称为离群值。例如，对于箱线图，离群值是那些离箱体边界太远的数据点（参见第20页的“百分位数与箱线图”），其中“太远”是指“超过四分位距的1.5倍”。在回归中，标准化残差是通常用于判断一条记录是否被归类为离群值的指标。标准化残差可以被解释为“距离回归线有多少个标准误”。

让我们在 R 中对邮政编码98105的所有房屋销售数据拟合一个回归模型：

1
2
3
house_98105 <- house[house$ZipCode == 98105,]
lm_98105 <- lm(AdjSalePrice ~ SqFtTotLiving + SqFtLot + Bathrooms +
Bedrooms + BldgGrade, data=house_98105)

在 Python 中：

1
2
3
4
5
6
house_98105 = house.loc[house['ZipCode'] == 98105, ]
predictors = ['SqFtTotLiving', 'SqFtLot', 'Bathrooms', 'Bedrooms', 'BldgGrade']
outcome = 'AdjSalePrice'
house_outlier = sm.OLS(house_98105[outcome],
house_98105[predictors].assign(const=1))
result_98105 = house_outlier.fit()

我们使用 R 中的 rstandard 函数提取标准化残差，并使用 order 函数获取最小残差的索引：

1
2
3
4
5
sresid <- rstandard(lm_98105)
idx <- order(sresid)
sresid[idx[1]]
20429
-4.326732

在 statsmodels 中，使用 OLSInfluence 来分析残差：

1
2
3
influence = OLSInfluence(result_98105)
sresiduals = influence.resid_studentized_internal
sresiduals.idxmin(), sresiduals.min()

模型中最大的高估值比回归线高出四个多标准误，这相当于高估了$757,754。与此离群值对应的原始数据记录在 R 中如下：

1
2
3
4
5
house_98105[idx[1], c('AdjSalePrice', 'SqFtTotLiving', 'SqFtLot',
'Bathrooms', 'Bedrooms', 'BldgGrade')]
AdjSalePrice SqFtTotLiving SqFtLot Bathrooms Bedrooms BldgGrade
(dbl) (int) (int) (dbl) (int) (int)
20429 119748 2900 7276 3 6 7

在 Python 中：

1
2
3
outlier = house_98105.loc[sresiduals.idxmin(), :]
print('AdjSalePrice', outlier[outcome])
print(outlier[predictors])

在这种情况下，似乎这条记录出了问题：在这个邮政编码中，如此大小的房屋通常售价要远高于$119,748。图4-4展示了此次销售的法定契据摘录：很明显，此次销售仅涉及该房产的部分权益。在这种情况下，该离群值对应一次异常销售，不应被包含在回归分析中。离群值也可能是由其他问题造成的，例如“粗心”的数据录入或单位不匹配（例如，以千美元为单位报告销售额而不是以美元为单位）。

F4.4

对于大数据问题，离群值通常不会对用于预测新数据的回归拟合造成问题。然而，在异常检测中，离群值是核心，因为找到离群值正是其全部目的。离群值也可能对应于欺诈或意外行为。无论如何，检测离群值可能是一个关键的商业需求。

影响力值

Influential Values

如果一个值在被移除后会显著改变回归方程，那么它就被称为有影响力的观测值。在回归中，这样的值不一定与大的残差相关联。例如，考虑图4-5中的两条回归线。实线对应于使用所有数据拟合的回归，而虚线对应于移除了右上角数据点后的回归。很明显，这个数据值对回归有巨大的影响，尽管它本身并不是一个大的离群值（从完整回归的角度来看）。这个数据值被认为对回归具有高杠杆。

F4.5

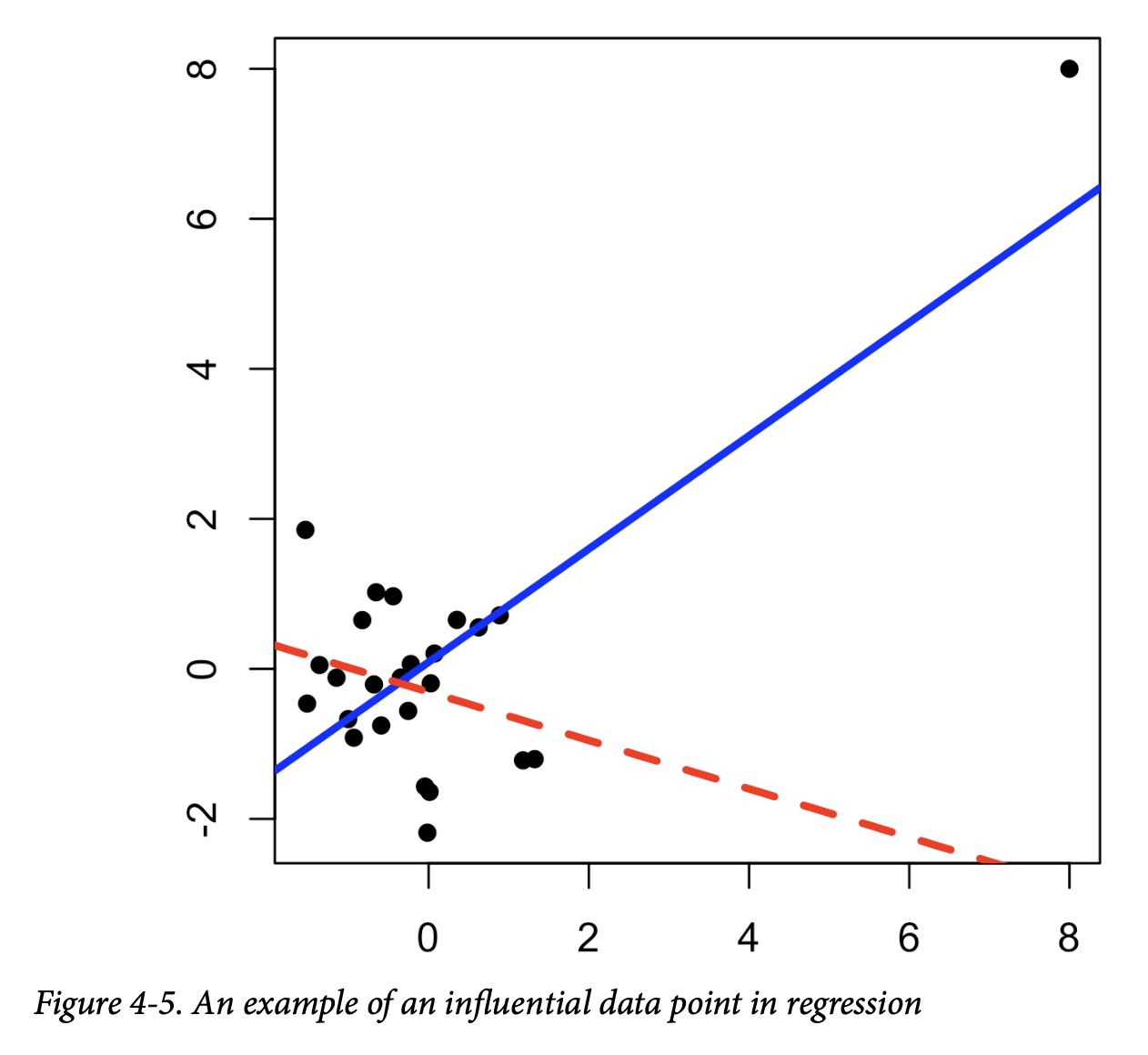
除了标准化残差（参见第177页的“离群值”）之外，统计学家还开发了几个指标来确定单个记录对回归的影响。一个常见的杠杆度量是帽子值（hat-value）；当帽子值高于 \(2(P+1)/n\) 时，表明该数据值具有高杠杆。

另一个指标是库克距离（Cook’s distance），它将影响力定义为杠杆值和残差大小的组合。一个经验法则是，如果库克距离超过 \(4/(n-P-1)\)，则该观测值具有高影响力。

F4.6

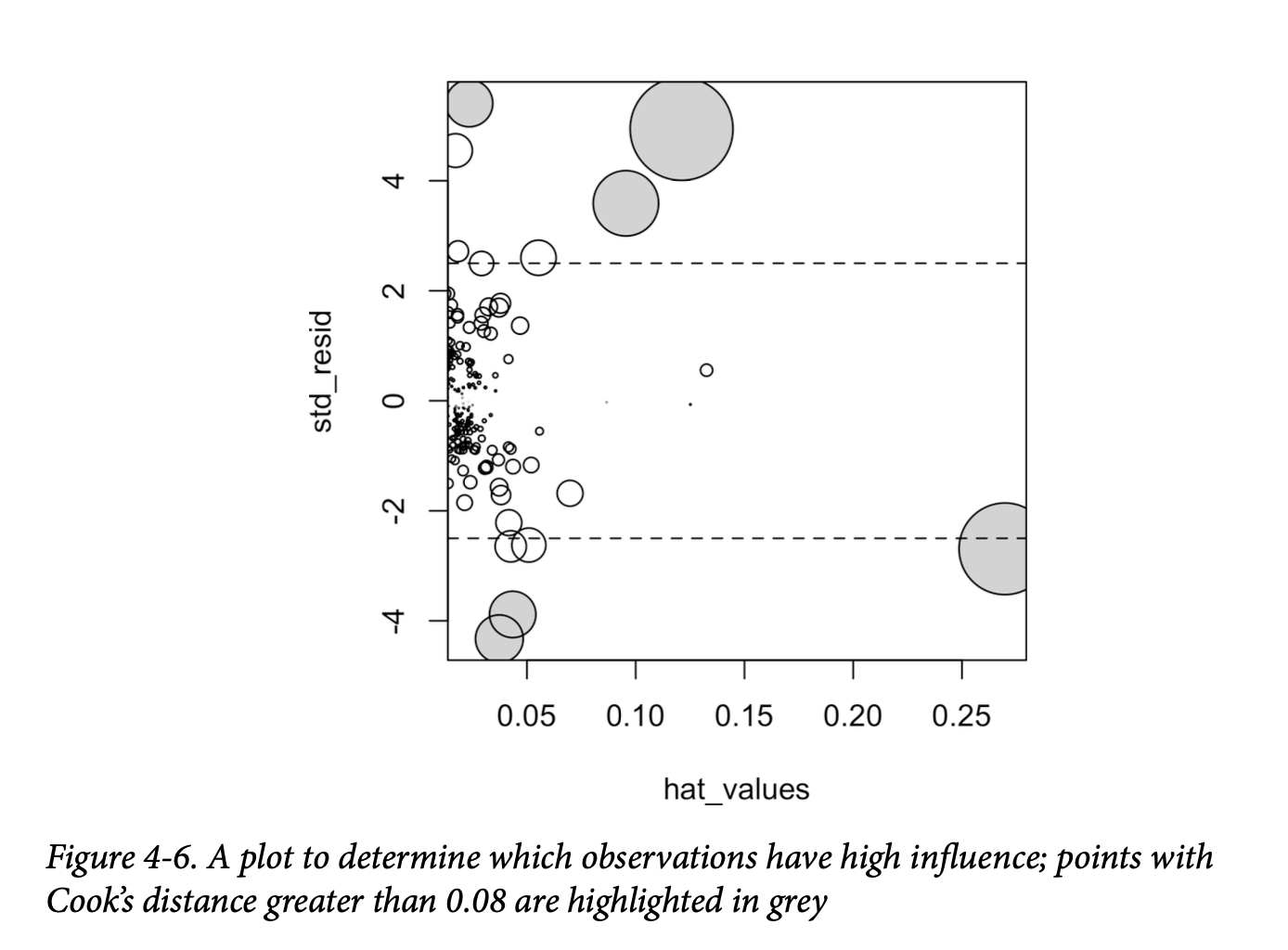
影响力图（或气泡图）(influence plot or bubble plot)将标准化残差、帽子值和库克距离组合在一个图表中。图4-6展示了金县房屋数据的影响力图，可以用以下 R 代码创建：

1
2
3
4
5
6
7
8
std_resid <- rstandard(lm_98105)
cooks_D <- cooks.distance(lm_98105)
hat_values <- hatvalues(lm_98105)
plot(subset(hat_values, cooks_D > 0.08), subset(std_resid, cooks_D > 0.08),
xlab='hat_values', ylab='std_resid',
cex=10*sqrt(subset(cooks_D, cooks_D > 0.08)), pch=16, col='lightgrey')
points(hat_values, std_resid, cex=10*sqrt(cooks_D))
abline(h=c(-2.5, 2.5), lty=2)

以下是创建类似图表的 Python 代码：

1
2
3
4
5
6
7
8
9
10
11
influence = OLSInfluence(result_98105)
fig, ax = plt.subplots(figsize=(5, 5))
ax.axhline(-2.5, linestyle='--'
, color='C1')
ax.axhline(2.5, linestyle='--'
, color='C1')
ax.scatter(influence.hat_matrix_diag, influence.resid_studentized_internal,
s=1000 * np.sqrt(influence.cooks_distance[0]),
alpha=0.5)
ax.set_xlabel('hat values')
ax.set_ylabel('studentized residuals')

图中有几个数据点明显对回归表现出较大的影响力。库克距离可以使用 cooks.distance 函数计算，你可以使用 hatvalues 来计算诊断值。帽子值绘制在 x 轴上，残差绘制在 y 轴上，点的大小与库克距离的值相关。

T4.2

表4-2比较了使用完整数据集和移除了高影响力数据点（库克距离 > 0.08）的回归结果。 Bathrooms 的回归系数变化相当大。

为了拟合一个能够可靠预测未来数据的回归模型，识别有影响力的观测值仅在较小的数据集中有用。对于包含许多记录的回归模型，单个观测值不太可能具有足够的权重来对拟合方程产生极端影响（尽管回归模型仍然可能存在大的离群值）。然而，对于异常检测而言，识别有影响力的观测值可能非常有用。

异方差性、非正态性与相关误差

Heteroskedasticity, Non-Normality, and Correlated Errors

统计学家们非常关注残差的分布。事实证明，在广泛的分布假设下，普通最小二乘法（OLS）（参见第148页的“最小二乘法”）是无偏的，并且在某些情况下是“最优”的估计量。这意味着在大多数问题中，数据科学家无需过度关注残差的分布。

残差的分布主要关系到正式统计推断（假设检验和 p 值）的有效性，而这对于主要关注预测准确性的数据科学家来说，其重要性是最小的。正态分布的误差是一个信号，表明模型是完整的；而非正态分布的误差则表明模型可能遗漏了某些东西。为了使正式推断完全有效，残差被假定为正态分布、具有相同的方差且相互独立。数据科学家可能需要关注这一点的一个领域是预测值的标准置信区间计算，它基于关于残差的这些假设（参见第161页的“置信区间与预测区间”）。

异方差性（Heteroskedasticity）是指在预测值的整个范围内缺乏恒定的残差方差。换句话说，在某些范围内的误差比其他范围更大。将数据可视化是分析残差的一种便捷方式。

以下 R 代码绘制了第177页“离群值”中拟合的 lm_98105 回归模型的绝对残差与预测值之间的关系图：

1
2
df <- data.frame(resid = residuals(lm_98105), pred = predict(lm_98105))
ggplot(df, aes(pred, abs(resid))) + geom_point() + geom_smooth()

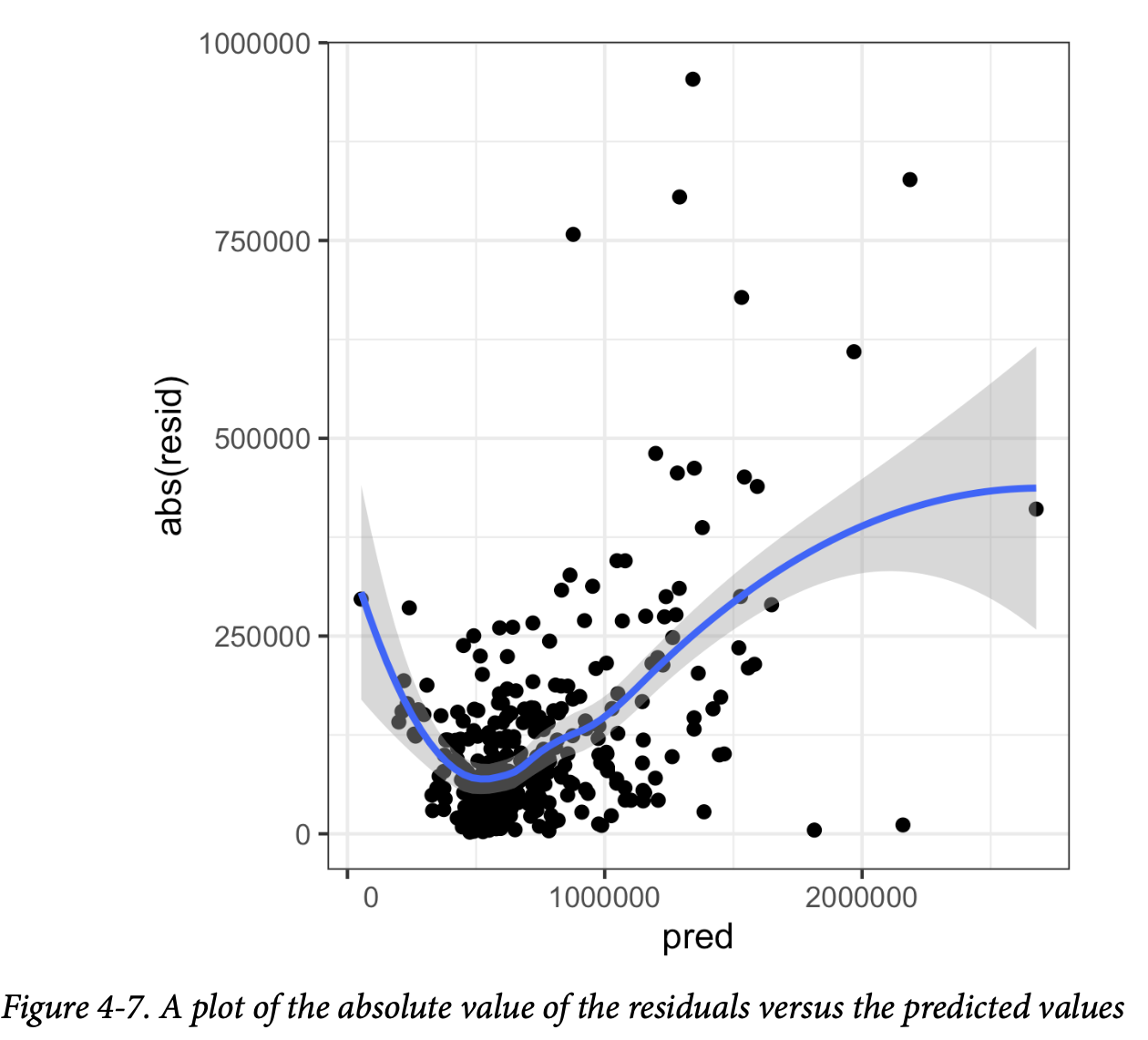
图4-7显示了生成的图。使用 geom_smooth，可以很容易地叠加一个绝对残差的平滑曲线。该函数调用 loess 方法（局部加权散点图平滑），以在散点图中生成 x 轴和 y 轴变量之间关系的平滑估计（参见第185页的“散点图平滑器”）。

F4.7

在 Python 中，seaborn 包的 regplot 函数可以创建类似的图：

1
2
3
4
5
6
fig, ax = plt.subplots(figsize=(5, 5))
sns.regplot(result_98105.fittedvalues, np.abs(result_98105.resid),
scatter_kws={'alpha': 0.25}, line_kws={'color': 'C1'},
lowess=True, ax=ax)
ax.set_xlabel('predicted')
ax.set_ylabel('abs(residual)')

很明显，残差的方差随着房屋价值的升高而增大，但对于低价值的房屋也很大。这个图表明 lm_98105 存在异方差性误差。

知识点

为什么数据科学家要关心异方差性？**异方差性表明预测误差对于预测值的不同范围有所不同，这可能暗示模型不完整。例如，lm_98105 中的异方差性可能表明回归模型未能解释高价值和低价值房屋中遗漏的某些因素。

F4.8

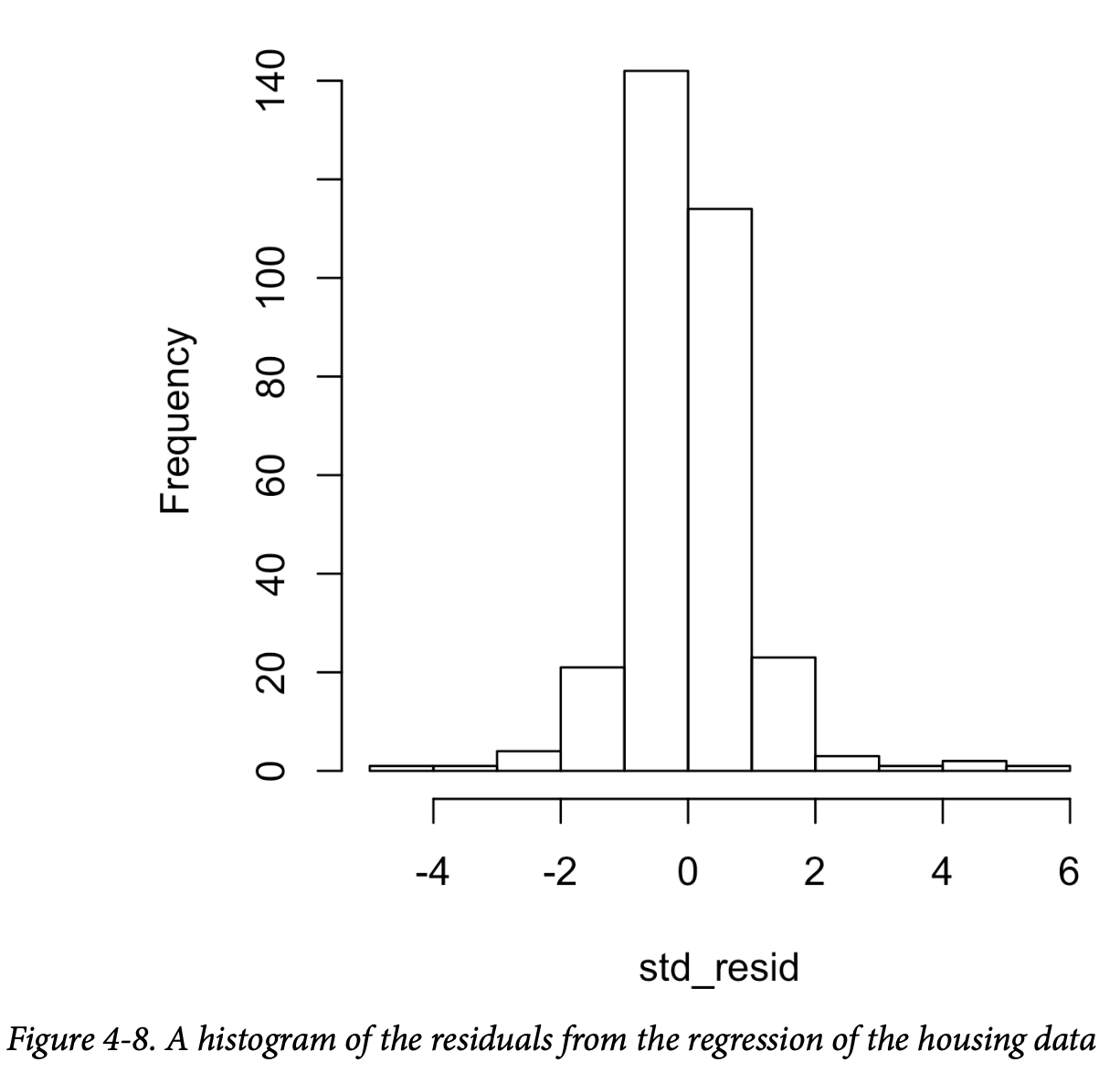
图4-8是 lm_98105 回归模型的标准化残差直方图。该分布的尾部明显比正态分布长，并且对较大的残差表现出轻微的偏斜。

统计学家也可能检查误差是否独立的假设。对于随时间或空间收集的数据尤其如此。德宾-沃森统计量（Durbin-Watson statistic）可用于检测涉及时间序列数据的回归中是否存在显著的自相关。如果回归模型的误差是相关的，那么这些信息对于进行短期预测可能很有用，并且应该被纳入模型中。有关如何将自相关信息纳入时间序列数据回归模型的更多信息，请参阅 Galit Shmueli 和 Kenneth Lichtendahl（Axelrod Schnall，2018）撰写的《实用时间序列预测与 R，第2版》。如果目标是长期预测或解释性模型，微观层面上过度的自相关数据可能会分散注意力。在这种情况下，可能需要进行平滑处理，或者从一开始就以较低的粒度收集数据。

即使回归模型违反了某个分布假设，我们是否应该关心呢？在数据科学中，兴趣主要在于预测准确性，因此对异方差性进行一些检查可能是必要的。你可能会发现数据中存在模型尚未捕获的某种信号。然而，仅仅为了验证正式统计推断（p 值、F 统计量等）而满足分布假设，对数据科学家来说并没有那么重要。

通用注解

散点图平滑器（Scatterplot Smoothers）：回归是关于建模响应变量和预测变量之间的关系。在评估回归模型时，使用散点图平滑器**以可视化方式突出两个变量之间的关系是很有用的。

例如，在图4-7中，绝对残差与预测值之间关系的平滑曲线显示，残差的方差取决于残差的值。在本例中，使用了 loess 函数；loess 通过重复拟合一系列局部回归到连续子集上来生成平滑曲线。虽然 loess 可能是最常用的平滑器，但 R 中还有其他散点图平滑器，例如 super smooth (supsmu) 和核平滑（kernel smoothing, ksmooth）。在 Python 中，我们可以在 scipy (wiener 或 sav) 和 statsmodels (kernel_regression) 中找到更多的平滑器。为了评估回归模型，通常无需担心这些散点图平滑器的具体细节。

偏残差图与非线性

Partial Residual Plots and Nonlinearity

偏残差图是一种可视化工具，用于评估估计的拟合效果，以及它如何解释一个预测变量与结果之间的关系。偏残差图的基本思想是隔离一个预测变量与响应变量之间的关系，同时考虑所有其他预测变量的影响。

偏残差可以被视为一个“合成结果”值，它结合了基于单个预测变量的预测值和完整回归方程的实际残差。预测变量 \(X_i\) 的偏残差是普通残差加上与 \(X_i\) 相关的回归项：

\[ \text{偏残差} = \text{残差} + b_i X_i \]

其中，\(b_i\) 是估计的回归系数。R 中的 predict 函数有一个选项可以返回单个回归项 \(b_i X_i\)：

1
2
terms <- predict(lm_98105, type='terms')
partial_resid <- resid(lm_98105) + terms

偏残差图将 \(X_i\) 预测变量显示在 x 轴上，偏残差显示在 y 轴上。使用 ggplot2 可以很容易地叠加偏残差的平滑曲线：

1
2
3
4
5
6
7
df <- data.frame(SqFtTotLiving = house_98105[, 'SqFtTotLiving'],
Terms = terms[, 'SqFtTotLiving'],
PartialResid = partial_resid[, 'SqFtTotLiving'])
ggplot(df, aes(SqFtTotLiving, PartialResid)) +
geom_point(shape=1) + scale_shape(solid = FALSE) +
geom_smooth(linetype=2) +
geom_line(aes(SqFtTotLiving, Terms))

statsmodels 包的 sm.graphics.plot_ccpr 方法可以创建类似的偏残差图：

1
sm.graphics.plot_ccpr(result_98105, 'SqFtTotLiving')

R 和 Python 的图表之间有一个常量偏移。在 R 中，添加了一个常量，使得项的均值为零。

F4.9

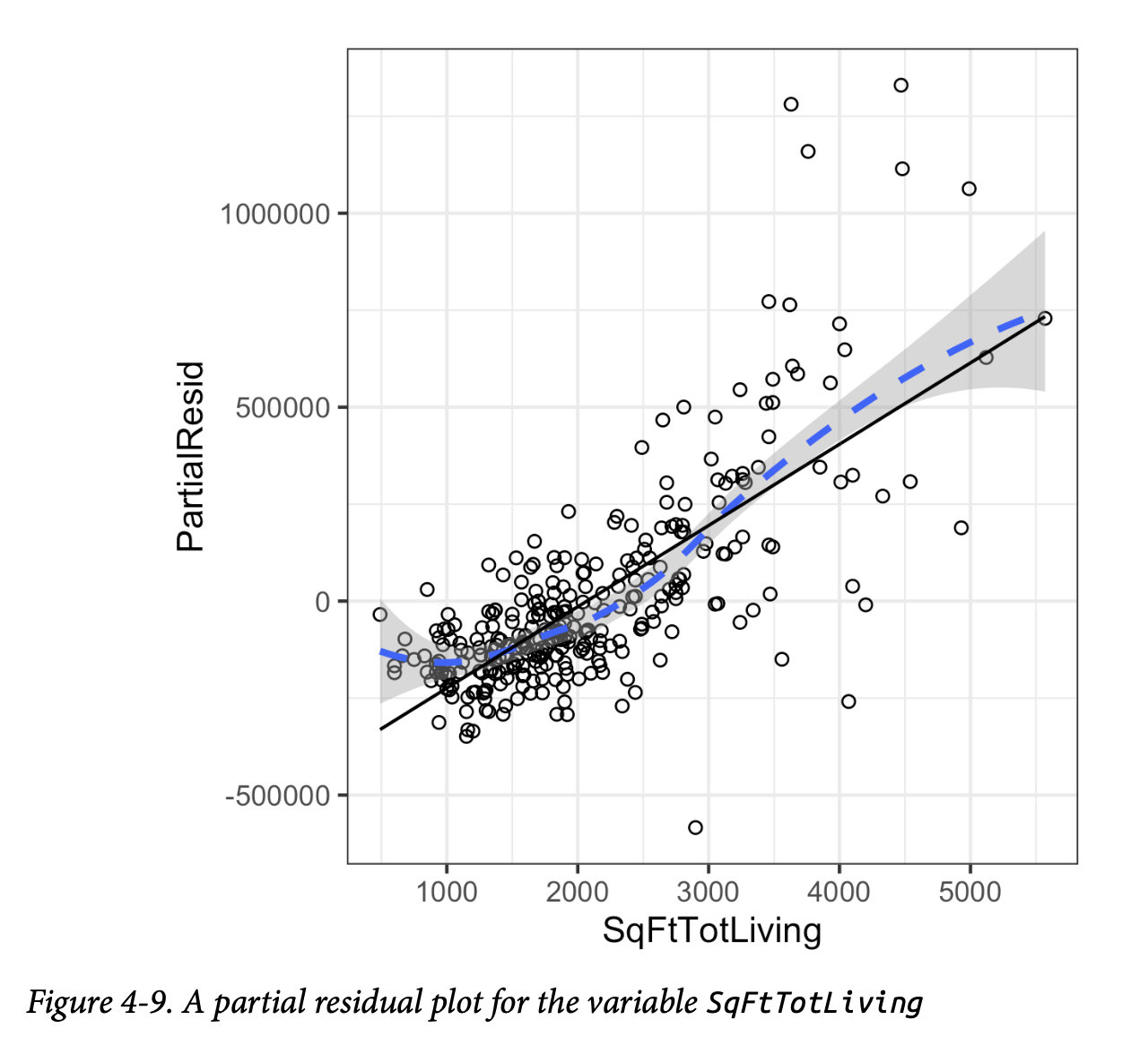
由此生成的图表如图4-9所示。偏残差是对 SqFtTotLiving 对销售价格贡献的估计。SqFtTotLiving 与销售价格之间的关系显然是非线性的（虚线）。回归线（实线）低估了面积小于1000平方英尺的房屋价格，并高估了面积在2000到3000平方英尺之间的房屋价格。由于4000平方英尺以上的数据点太少，无法得出结论。

这种非线性关系在这种情况下是合理的：在一栋小房子中增加500英尺与在一栋大房子中增加500英尺所带来的价值差异是巨大的。这表明，我们应该考虑使用非线性项来替代简单的 SqFtTotLiving 线性项（参见第187页的“多项式和样条回归”）。

关键思想

  • 离群值：虽然离群值可能会给小数据集带来问题，但其主要作用在于识别数据问题或定位异常情况。
  • 影响力：单个记录（包括回归离群值）在小数据集中可能对回归方程产生很大影响，但在大数据中这种影响会被稀释。
  • 残差分布：如果回归模型用于正式推断（p 值等），则应检查残差的分布假设。但总的来说，残差分布在数据科学中并不那么关键。
  • 偏残差图：可用于定性评估每个回归项的拟合效果，并可能导致模型的替代性设定。

多项式与样条回归

Polynomial and Spline Regression

响应变量与预测变量之间的关系不一定是线性的。例如，药物剂量与反应之间的关系通常是非线性的：将剂量加倍通常不会使反应也加倍。对产品的需求也不是营销投入的线性函数；在某个点之后，需求可能会饱和。有许多方法可以扩展回归模型以捕捉这些非线性效应。

非线性回归的关键术语

  • 多项式回归（Polynomial regression） 在回归模型中添加多项式项（平方、立方等）。
  • 样条回归（Spline regression） 用一系列多项式分段来拟合一条平滑曲线。
  • 结点（Knots） 分隔样条分段的值。
  • 广义加性模型（Generalized additive models） 具有自动选择结点的样条模型。 同义词：GAM

知识点

非线性回归（术语辨析）：当统计学家谈论非线性回归时，他们指的是不能使用最小二乘法进行拟合的模型。什么样的模型是非线性的？基本上，所有响应变量不能表示为预测变量或其某种变换的线性组合的模型都是非线性的。非线性回归模型更难拟合，计算也更密集，因为它需要数值优化**。因此，如果可能的话，通常首选使用线性模型。

多项式回归

Polynomial

多项式回归涉及在回归方程中包含多项式项。多项式回归的使用可以追溯到回归本身的发展时期，Gergonne 在1815年就发表了相关论文。例如，响应变量 Y 和预测变量 X 之间的二次回归方程形式如下： \[ Y = b_0 + b_1X + b_2X^2 + e \]

多项式回归可以在 R 中通过 poly 函数进行拟合。例如，以下代码为金县住房数据中的 SqFtTotLiving 拟合了一个二次多项式：

1
2
3
4
5
6
7
8
9
10
11
12
13
lm(AdjSalePrice ~ poly(SqFtTotLiving, 2) + SqFtLot +
BldgGrade + Bathrooms + Bedrooms,
data=house_98105)
Call:
lm(formula = AdjSalePrice ~ poly(SqFtTotLiving, 2) + SqFtLot +
BldgGrade + Bathrooms + Bedrooms, data = house_98105)
Coefficients:
(Intercept) poly(SqFtTotLiving, 2)1 poly(SqFtTotLiving, 2)2
-402530.47 3271519.49 776934.02
SqFtLot BldgGrade Bathrooms
32.56 135717.06 -1435.12
Bedrooms
-9191.94

在 statsmodels 中，我们使用 I(SqFtTotLiving**2) 将平方项添加到模型定义中：

1
2
3
4
5
model_poly = smf.ols(formula='AdjSalePrice ~ SqFtTotLiving + ' +
'+ I(SqFtTotLiving**2) + ' +
'SqFtLot + Bathrooms + Bedrooms + BldgGrade', data=house_98105)
result_poly = model_poly.fit()
result_poly.summary()

截距和多项式系数与 R 的结果不同。这是由于不同的实现方式造成的。剩余的系数和预测结果是等效的。

现在，SqFtTotLiving 有两个相关的系数：一个用于线性项，一个用于二次项。

偏残差图（参见第185页的“偏残差图与非线性”）显示，与 SqFtTotLiving 相关的回归方程中存在一些曲率。与线性拟合相比，拟合线（实线）更紧密地匹配偏残差的平滑曲线（虚线，参见第189页的“样条”）（见图4-10）。

F4.10

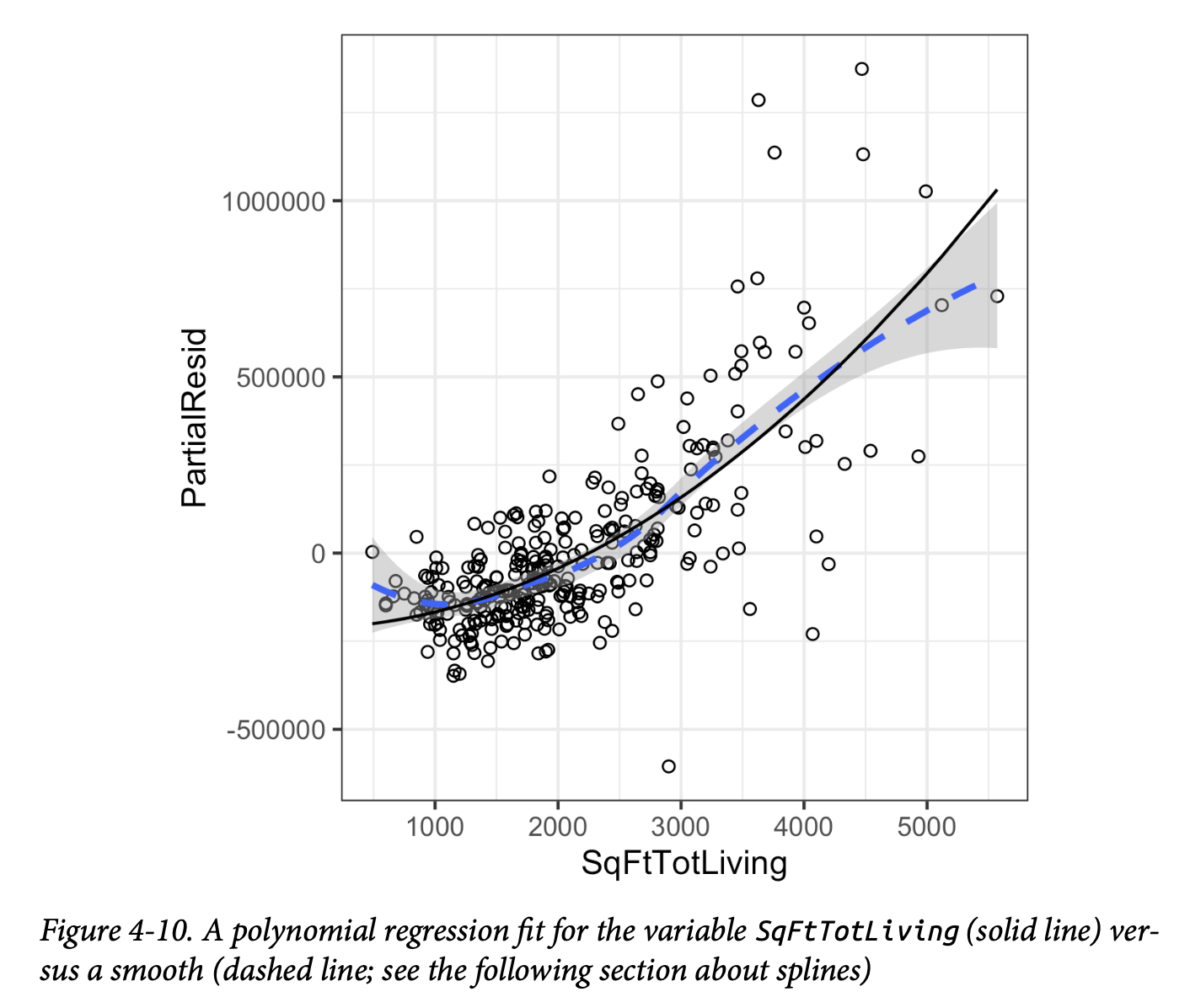
statsmodels 的实现只适用于线性项。随附的源代码提供了也适用于多项式回归的实现。

样条回归

Splines

多项式回归只能捕捉非线性关系中的特定曲率。添加更高阶的项，例如三次或四次多项式，常常会导致回归方程出现不必要的“弯曲”。另一种（通常更优越）的非线性关系建模方法是使用样条回归。样条提供了一种在固定点之间平滑插值的方法。样条最初被制图员用来绘制平滑曲线，尤其是在造船和飞机制造领域。

样条曲线是通过用被称为“鸭子”（ducks）的重物来弯曲一块薄木片而创建的；参见图4-11。

F4.11

样条的正式定义是一系列分段连续的多项式。它们最早由罗马尼亚数学家 I. J. Schoenberg 在二战期间于美国阿伯丁试验场开发。这些多项式分段在预测变量中的一系列（称为结点 knots）处平滑连接。样条的公式比多项式回归复杂得多；统计软件通常会处理拟合样条的细节。R 包 splines 包含了 bs 函数，用于在回归模型中创建 b 样条（基础样条）项。例如，以下代码为房屋回归模型添加了一个 b 样条项：

1
2
3
4
library(splines)
knots <- quantile(house_98105$SqFtTotLiving, p=c(.25, .5, .75))
lm_spline <- lm(AdjSalePrice ~ bs(SqFtTotLiving, knots=knots, degree=3) +
SqFtLot + Bathrooms + Bedrooms + BldgGrade, data=house_98105)

需要指定两个参数：多项式的次数和结点的位置。在这个例子中，预测变量 SqFtTotLiving 使用三次样条（degree=3）被包含在模型中。默认情况下，bs 会在边界处设置结点；此外，结点也被设置在下四分位数、中位数和上四分位数处。

statsmodels 的公式接口以类似于 R 的方式支持使用样条。在这里，我们使用 df（自由度）来指定 b 样条。这将创建 df - degree = 6 - 3 = 3 个内部结点，其位置的计算方式与上述 R 代码相同：

1
2
3
4
formula = 'AdjSalePrice ~ bs(SqFtTotLiving, df=6, degree=3) + ' +
'SqFtLot + Bathrooms + Bedrooms + BldgGrade'
model_spline = smf.ols(formula=formula, data=house_9105)
result_spline = model_spline.fit()

与线性项系数有直接意义不同，样条项的系数是不可解释的。相反，使用可视化展示来揭示样条拟合的性质更为有用。图4-12显示了回归模型的偏残差图。与多项式模型相比，样条模型更紧密地匹配平滑曲线，这展示了样条的更大灵活性。在这种情况下，拟合线更贴近数据。

F4.12

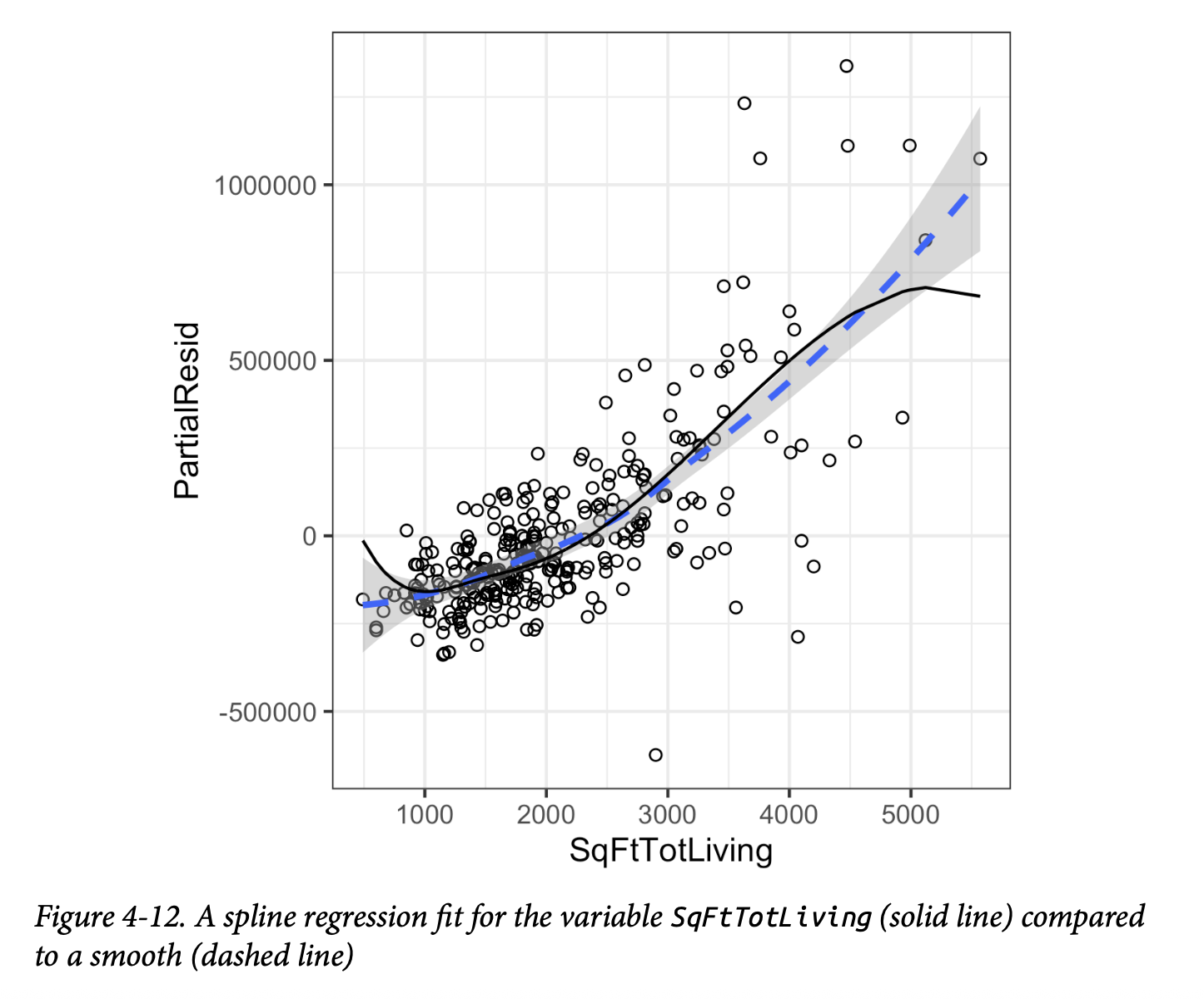
这是否意味着样条回归是一个更好的模型？不一定。从经济学角度来看，面积非常小的房屋（小于1000平方英尺）的价值高于稍大一些的房屋是没有道理的。这可能是一个混杂变量造成的假象；参见第172页的“混杂变量”。

广义加性模型

Generalized Additive Models

假设你通过先验知识或检查回归诊断，怀疑响应变量与某个预测变量之间存在非线性关系。多项式项可能不够灵活来捕捉这种关系，而样条项又需要指定结点。广义加性模型（Generalized Additive Models, GAM）是一种灵活的建模技术，可以用于自动拟合样条回归。R 中的 mgcv 包可用于将 GAM 模型拟合到住房数据上：

1
2
3
4
library(mgcv)
lm_gam <- gam(AdjSalePrice ~ s(SqFtTotLiving) + SqFtLot +
Bathrooms + Bedrooms + BldgGrade,
data=house_98105)

s(SqFtTotLiving) 项告诉 gam 函数为样条项寻找“最佳”结点。

在 Python 中，我们可以使用 pyGAM 包。它提供了回归和分类的方法。在这里，我们使用 LinearGAM 来创建一个回归模型：

1
2
3
4
5
6
predictors = ['SqFtTotLiving', 'SqFtLot', 'Bathrooms', 'Bedrooms', 'BldgGrade']
outcome = 'AdjSalePrice'
X = house_98105[predictors].values
y = house_98105[outcome]
gam = LinearGAM(s(0, n_splines=12) + l(1) + l(2) + l(3) + l(4))
gam.gridsearch(X, y)

n_splines 的默认值是20。这对于较大的 SqFtTotLiving 值会导致过拟合。而12这个值可以得到一个更合理的拟合效果。

关键思想

  • 离群值：回归中的离群值是具有大残差的记录。
  • 多重共线性：可能导致回归方程拟合时的数值不稳定。
  • 混杂变量：一个从模型中遗漏的重要预测变量，可能导致回归方程中出现虚假关系。
  • 交互项：如果一个变量的效果取决于另一个变量的水平或大小，则需要引入两个变量之间的交互项。
  • 多项式回归：可以拟合预测变量和结果变量之间的非线性关系。
  • 样条回归：是连接在结点上的一系列多项式分段。
  • 广义加性模型（GAM）：我们可以使用广义加性模型来自动化样条中指定结点的过程。

总结

在所有统计方法中，回归可能是多年来使用最广泛的一种方法。它旨在建立多个预测变量与一个结果变量之间的关系。其基本形式是线性的：每个预测变量都有一个系数来描述该预测变量与结果之间的线性关系。更高级的回归形式，如多项式和样条回归，允许这种关系是非线性的。在经典统计学中，重点在于找到对观察数据的一个良好拟合，以解释或描述某个现象，并且这种拟合的强度是通过传统的样本内指标来评估的。相比之下，在数据科学中，目标通常是预测新数据的值，因此使用基于样本外数据的预测准确性指标来进行模型评估。变量选择方法则用于降维和创建更紧凑的模型。