第2章 数据与抽样分布

《Practical Statistics for Data Scientists》书籍英文版
《面向数据科学家的实用统计学》中文版书籍

第 2 章 数据与抽样分布

人们常见的一个误解是，大数据时代意味着不再需要抽样。事实上，数据在质量和相关性上呈现爆炸式增长，反而强化了抽样作为高效处理各种数据并最小化偏差的工具的重要性。即使在大数据项目中，预测模型通常也是用样本开发和试运行的。样本还用于各种测试（例如，比较不同网页设计对点击率的影响）。

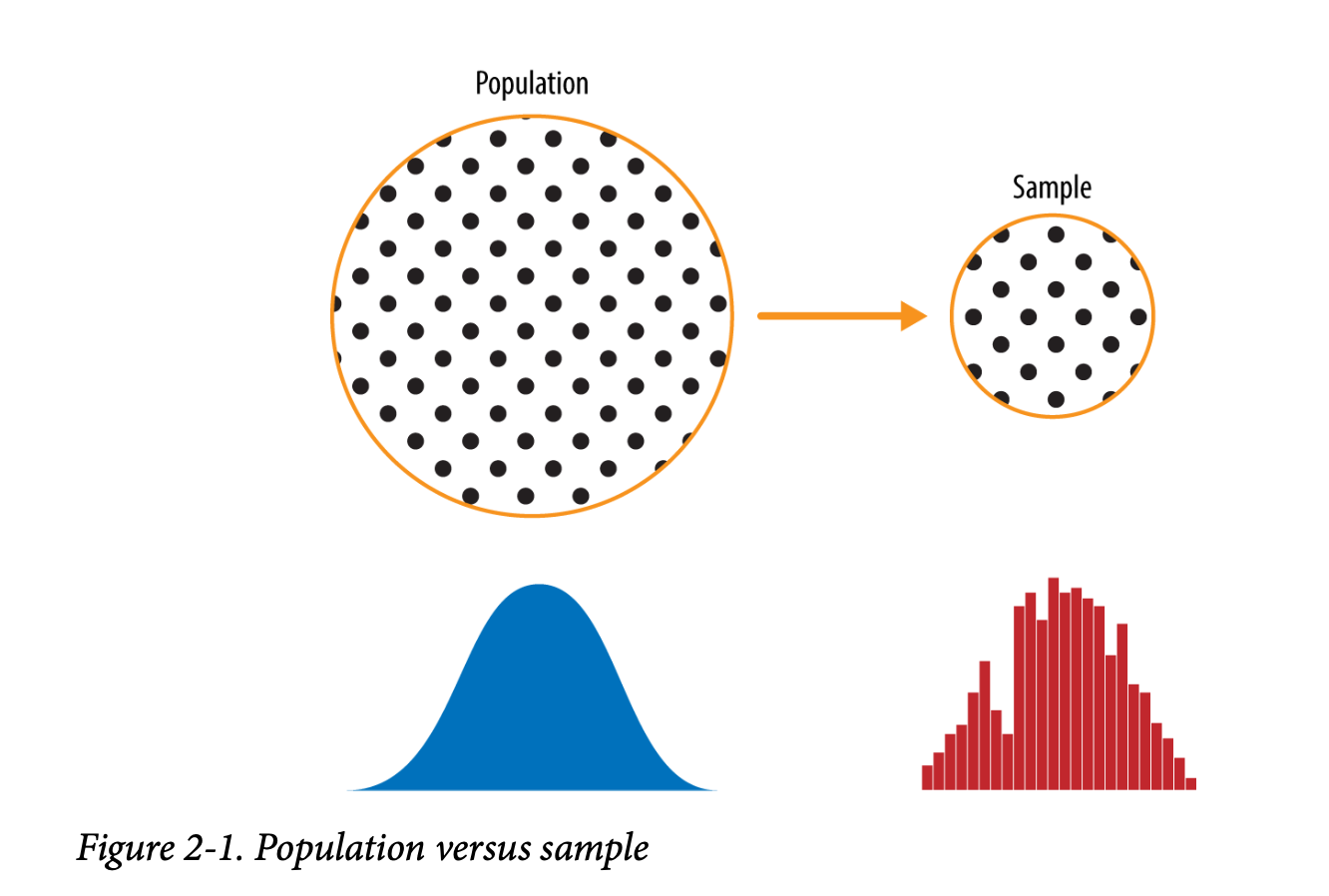
图 2-1 展示了支撑本章所讨论概念——数据与抽样分布——的示意图。左侧表示总体，在统计学中假定总体遵循某个潜在但未知的分布。我们唯一能获取的是右侧所示的样本数据及其经验分布。要从左侧到达右侧，需要一个抽样过程（由箭头表示）。传统统计学非常注重左侧，依赖于对总体作出强假设的理论。现代统计学则更多地转向右侧，不再需要这些假设。

总体而言，数据科学家不必担心左侧的理论性质，而应关注抽样过程和手头的数据。不过也有一些显著例外。有时数据源自可以建模的物理过程。最简单的例子是掷硬币：它服从二项分布。任何现实中的二项情境（购买或不购买、欺诈或非欺诈、点击或不点击）都可以有效地用一枚硬币来建模（当然，硬币正面出现的概率可调整）。在这些情况下，我们可以通过理解总体获得更多洞见。

随机抽样与样本偏差

样本是来自更大数据集的一个子集；统计学家把这个更大的数据集称为总体。统计学中的总体并不等同于生物学中的“种群”——它是一个庞大、明确定义的（有时是理论的或假想的）数据集合。

随机抽样是一个过程，其中总体中每一个可供抽取的成员在每次抽取时都有相等的机会被选入样本。由此得到的样本称为简单随机样本。抽样可以有放回进行，即每次抽取后将观测值放回总体中以便未来可能再次被选中；也可以无放回进行，即一旦被抽取就不再返回总体，无法再次抽取。

在基于样本进行估计或建模时，数据质量往往比数据数量更重要。数据科学中的数据质量包括完整性、格式一致性、整洁性和单个数据点的准确性。统计学还增加了“代表性”的概念。

随机抽样关键术语

• 样本（Sample） 从更大数据集中抽取的子集。

• 总体（Population） 更大的数据集或数据集的概念。

• N（n） 总体（样本）的大小。

• 随机抽样（Random sampling） 随机将总体元素抽取进样本。

• 分层抽样（Stratified sampling） 将总体划分为若干层（strata），并从每一层随机抽样。

• 层（Stratum，复数 strata） 总体中具有共同特征的同质子群。

• 简单随机样本（Simple random sample） 直接从总体随机抽取、不分层而得到的样本。

• 偏差（Bias） 系统性误差。

• 样本偏差（Sample bias） 样本对总体的错误代表或失真。

最经典的例子是 1936 年《文学文摘》（Literary Digest）的民意调查，该调查预测阿尔夫·兰登（Alf Landon）将战胜富兰克林·罗斯福（Franklin Roosevelt）。《文学文摘》当时是一份颇有影响力的期刊，它调查了其全部订阅者外加其他名单上的个人，总计超过 1000 万人，预测兰登将以压倒性优势获胜。而盖洛普民意调查（Gallup Poll）的创始人乔治·盖洛普（George Gallup）每两周仅对 2000 人进行调查，却准确预测了罗斯福的胜利。区别在于受访对象的选择方式。

《文学文摘》追求数量，却几乎不关注抽样方法。他们最终调查的对象多为社会经济地位相对较高的人群（他们自己的订阅者，加上那些因拥有电话和汽车等奢侈品而出现在营销名单上的人）。结果造成了样本偏差：样本在某些有意义且非随机的方面与它本应代表的总体不同。这里“非随机”一词很重要——几乎没有任何样本（包括随机样本）能完全代表总体。样本偏差发生在这种差异具有意义时，并且可以预期在用同样方法抽取的其他样本中继续存在。

通用注解：

自我选择抽样偏差（Self-Selection Sampling Bias）：你在 Yelp 等社交媒体网站上看到的餐馆、酒店、咖啡馆等评论容易产生偏差，因为提交评论的人并不是随机选择的；相反，是他们自己主动撰写的。这就导致了自我选择偏差**：有动机写评论的人可能经历过糟糕的体验，可能与该商家有某种关系，或者本身与不写评论的人群在特质上不同。需要注意的是，尽管自我选择样本作为反映真实情况的指标可能不可靠，但在比较一家店与另一家类似店时可能更可靠——因为同样的自我选择偏差可能同时适用于二者。

偏差

统计偏差是指由测量或抽样过程系统性地产生的测量或抽样误差。要区分随机机会造成的误差与偏差造成的误差。想象一个物理过程：一把枪射击靶子。它不会每次都击中靶心，甚至大多数时候都不会。一个无偏的过程也会产生误差，但这些误差是随机的，不会明显偏向某个方向（见图 2-2）。图 2-3 展示了一个有偏过程——在 x 和 y 方向仍存在随机误差，但还存在偏差：子弹往往落在右上象限。

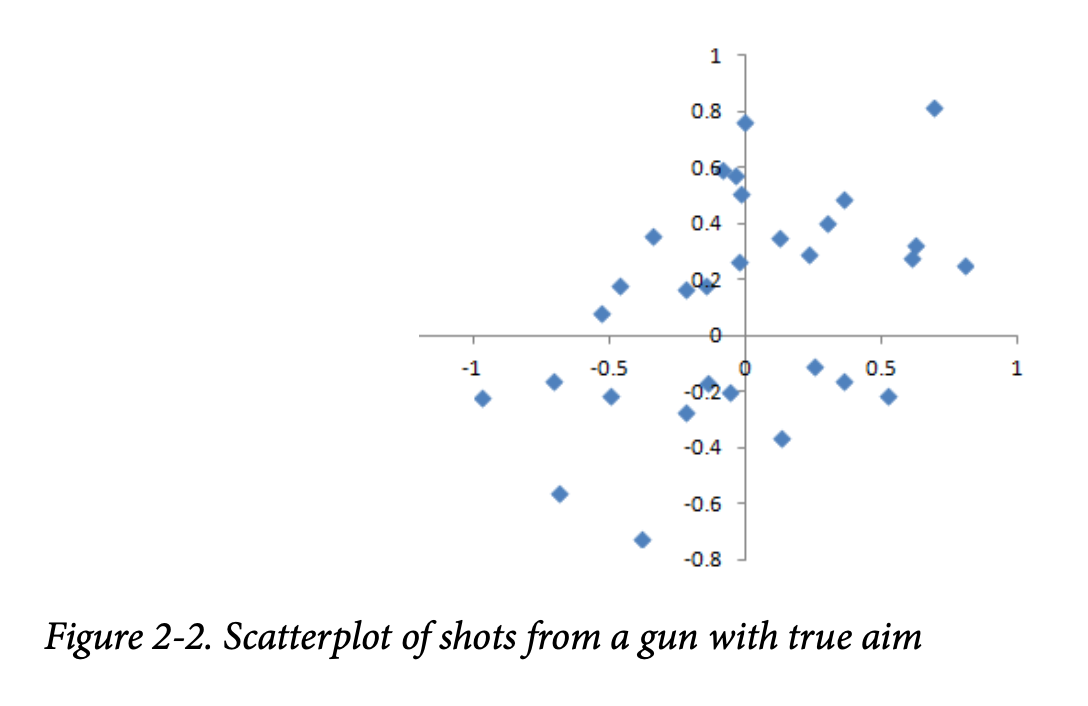
偏差有不同的形式，可能是可观察的，也可能是不可见的。当结果显示出偏差迹象时（例如，通过与基准或实际值对比），通常意味着统计或机器学习模型被错误设定，或有重要变量被遗漏。

随机选择

为了避免导致《文学文摘》预测兰登获胜的样本偏差，乔治·盖洛普（见图 2-4）采用了更科学的抽样方法，以获得代表美国选民的样本。如今已有多种方法实现代表性，但其核心都是随机抽样。

随机抽样并非总是容易。正确定义可接触的总体是关键。假设我们想生成客户的代表性画像并需要进行一次试点客户调查。调查需要具有代表性，但工作量很大。

首先，我们需要定义谁是客户。我们可能选择所有购买金额 > 0 的客户记录。是否包含所有过去客户？是否包含退款？内部测试购买？经销商？既包括结算代理人又包括客户？

接下来，我们需要指定抽样程序。可能的做法是“随机选择 100 个客户”。当涉及从数据流中抽样（例如实时客户交易或网页访问者）时，时间因素可能很重要（例如，工作日早上 10 点的网页访问者可能与周末晚上 10 点的访问者不同）。

在分层抽样中，总体被划分为若干层，从每一层随机抽取样本。政治民调人员可能希望了解白人、黑人和西班牙裔的选举偏好。从总体中简单随机抽样得到的黑人和西班牙裔人数可能过少，因此可以在分层抽样中对这些层进行加权抽样，以获得等量的样本。

规模与质量：什么时候“规模”才重要？

在大数据时代，有时候“小”反而更好。花时间和精力进行随机抽样不仅能减少偏差，还能让我们有更多精力关注数据探索和数据质量。例如，缺失数据和异常值可能包含有用信息。若要在几百万条记录中追踪缺失值或检查异常值，成本可能高得无法承受；但如果是在几千条记录的样本中，这样做或许可行。如果数据量过大，数据绘图和人工检查都会变得缓慢。

那么，什么时候需要海量数据？

经典的“大数据”价值场景，是数据不仅庞大，而且稀疏。想想谷歌收到的搜索查询：列是词语，行是单个搜索查询，单元格值为 0 或 1（取决于该查询是否包含某个词）。目标是为某个查询确定最佳预测的搜索结果。英语单词超过 15 万个，谷歌每年处理超过一万亿次查询，这形成了一张巨大的矩阵，其中绝大多数条目都是“0”。

这是一个真正的大数据问题——只有在积累了如此庞大的数据量后，才能为大多数查询返回有效搜索结果。而且数据越多，结果越好。对于热门搜索词，这不是大问题——对某些极受关注的热门话题，有效数据很快就能找到。现代搜索技术真正的价值在于：它能为海量多样的搜索查询返回详细而有用的结果，包括那些出现频率只有百万分之一的查询。

比如搜索短语 “Ricky Ricardo and Little Red Riding Hood”。在互联网早期，这个查询可能只会返回关于乐队领队 Ricky Ricardo、他出演的电视节目《我爱露西（I Love Lucy）》以及儿童故事《小红帽》的结果。前两个主题各自都有很多搜索，但这两个关键词的组合却几乎没人搜过。而如今，随着数万亿条搜索查询的积累，这个查询能直接返回《我爱露西》里 Ricky 以英语和西班牙语混合的滑稽方式给婴儿讲述《小红帽》的那一集。

要知道，真正相关的记录（即包含这个确切搜索查询或非常相似的查询，并附带用户最终点击了哪个链接的信息）可能只需几千条就足以产生有效结果。然而，要得到这些相关记录，需要采集数万亿个数据点（当然，随机抽样在这种场景下毫无帮助）。另见第 73 页“长尾分布”。

样本均值与总体均值

符号 \(\bar{x}\)（读作“x-bar”）用于表示某总体样本的均值(the mean of a sample from a population)，而 \(\mu\) 则用于表示总体的均值。为什么要区分？因为样本信息是观察到的，而关于庞大总体的信息往往是通过较小样本推断的。统计学家喜欢在符号上把两者分开。

关键思想

• 即便在大数据时代，随机抽样仍然是数据科学家的重要武器之一。
• 偏差是当测量或观察不具有总体代表性时所导致的系统性误差。
• 数据质量往往比数据数量更重要；随机抽样可以减少偏差，并促进质量改进，否则这种改进的成本可能高得难以承担。

选择偏差

用棒球运动员尤吉·贝拉（Yogi Berra）的话改写一下：如果你不知道自己在找什么，只要找得够久，总能找到点东西。

选择偏差是指有意识或无意识地以某种方式选择数据，从而得出具有误导性或短暂性的结论。

选择偏差相关术语

• 选择偏差（Selection bias） 由于观测样本的选择方式所引入的偏差。

• 数据探查（Data snooping） 在数据中大范围“狩猎”，寻找某些有趣现象的过程。

• 大范围搜索效应（Vast search effect） 由于反复建立模型或在含大量自变量的数据上建模而导致的偏差或不可重复性。

如果你事先提出假设并设计良好的实验来验证它，你就可以对结论有较高的信心。然而，现实中往往并非如此。通常，人们会先看现有的数据，再试图找出模式。但这些模式是真的？还是只是数据探查（在数据里反复“挖掘”，直到出现某些有趣的东西）的产物？统计学家有句玩笑话：“如果你足够折磨数据，数据迟早会招供。”

实验验证的现象与在现有数据中发现的现象之间的区别，可以通过下面这个思想实验来说明：

设想有人告诉你，他能连续掷 10 次硬币都正面朝上。你当场挑战他（相当于做了一个实验），结果他真的连续 10 次正面朝上。显然你会认为他有某种特殊能力——因为连续 10 次掷硬币都是正面的概率仅为 1/1,000。

现在再设想一个体育场的播音员让在场的 20,000 名观众各自掷 10 次硬币，并在连续 10 次正面朝上的时候向引座员报告。某个人得到连续 10 次正面的概率极高（超过 99%，即 1 减去“没有任何人连续 10 次正面”的概率）。显然，事后选择体育场里那个（或那些）掷出 10 次正面的人，并不能说明他们有特殊能力——他们大概率只是运气好。

因为在数据科学中反复审视大型数据集本身就是重要价值之一，选择偏差是值得担心的问题。数据科学家尤其要注意一种特殊的选择偏差，即约翰·埃尔德（Elder Research 创始人，一家知名数据挖掘咨询公司）所说的“大范围搜索效应”。如果你在一个大型数据集上反复跑不同的模型、问不同的问题，你总能找到些“有趣的”东西。但这个结果是真正有意义的吗，还是偶然的离群值？

我们可以通过留出集（holdout set）来验证模型性能（有时甚至要使用多个留出集），以防止这种情况。埃尔德还提倡使用他称之为“目标打乱（target shuffling）”的方法（本质上是一种置换检验(a permutation test)），来测试数据挖掘模型所提示的预测关系是否有效。

在统计学中，除了“大范围搜索效应”之外，常见的选择偏差形式还包括：

• 非随机抽样（参见第 48 页“随机抽样与样本偏差”）
• 挑拣数据（cherry-picking）
• 选择能够突出某种统计效应的时间区间
• 当结果看起来“有趣”时就提前停止实验

均值回归

均值回归指的是对同一个变量进行连续测量时出现的一种现象：极端的观测值往往会被更接近中心的值所跟随。对极端值赋予特殊关注和意义可能会导致一种选择偏差。

体育迷们熟悉“年度最佳新秀，次年低潮”这一现象。在某一赛季开始职业生涯的运动员（新秀群体）中，总有一位表现优于所有其他人。通常，这位“年度最佳新秀”在第二年表现不如第一年。为什么？

几乎在所有主要的球类或冰球类运动中，总体表现都由两个因素共同作用：

• 技能
• 运气

均值回归是某种形式的选择偏差的结果。当我们选出表现最好的新秀时，技能和好运可能都在起作用。在他的下一赛季中，技能依然存在，但好运往往不再出现，所以他的表现会下降——即“回归”了。这个现象最早由弗朗西斯·高尔顿（Francis Galton）在 1886 年提出 [Galton-1886]，他在遗传倾向的研究中写到这一现象；例如，极高个男性的子女往往没有父亲那么高（见图 2-5）。

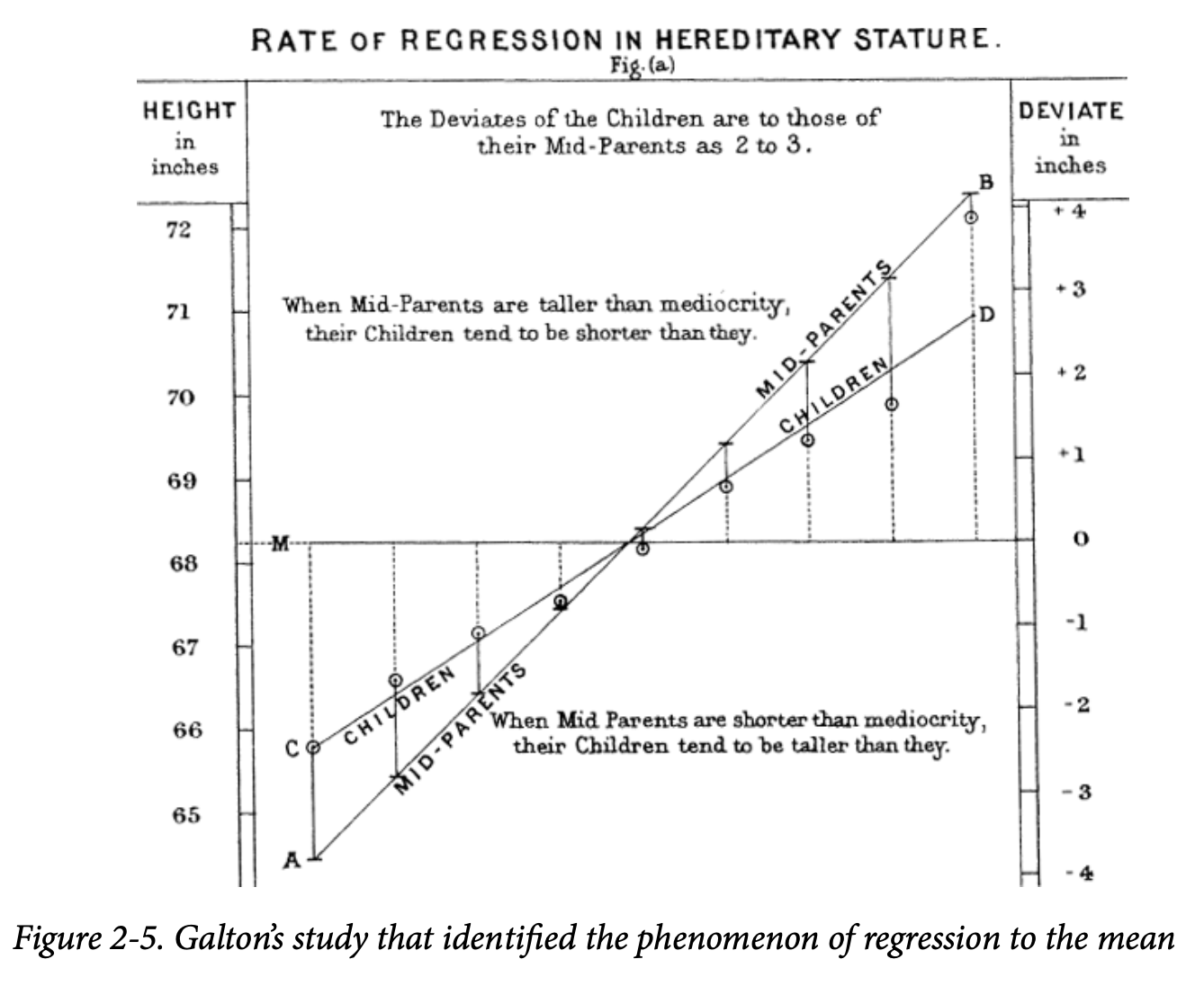
“均值回归”意为“回到（平均值）”，它与统计建模方法中的线性回归是不同的，后者指的是估计预测变量与结果变量之间的线性关系。

关键思想

• 在制定假设后再按随机化和随机抽样原则收集数据，可以避免偏差。
• 所有其他形式的数据分析都可能因数据收集/分析过程而产生偏差（例如在数据挖掘中重复运行模型、研究中的数据探查、以及事后选择有趣事件）。

统计量的抽样分布

“统计量的抽样分布”指的是从同一总体中抽取大量样本后，某个样本统计量的分布。传统统计学的许多内容都关注如何从（小）样本推断到（非常大）总体。

抽样分布的关键术语

• 样本统计量（Sample statistic） 从更大总体中抽取的样本数据计算得出的度量。

• 数据分布（Data distribution） 数据集中单个值的频率分布。

• 抽样分布（Sampling distribution） 某个样本统计量在许多样本或重采样中的频率分布。

• 中心极限定理（Central limit theorem） 随着样本量增加，抽样分布趋于正态分布的趋势。

• 标准误（Standard error） 某个样本统计量在许多样本中的变异性（标准差），不要与“标准差”混淆，后者指的是单个数据值的变异性。

通常，我们抽取样本的目的是测量某些东西（用样本统计量）或建立模型（用统计或机器学习模型）。由于我们的估计或模型是基于样本的，它可能存在误差；如果我们抽取不同的样本，结果可能会不同。因此，我们关心这种差异的大小——一个关键问题就是抽样变异性（sampling variability）。如果我们有大量数据，就可以抽取更多样本并直接观察某个样本统计量的分布。

通常情况下，如果有大量的数据，那么我们可以从中抽取更多的样本，进而直接观察样本统计量的分布情况。只要数据易于获取，那么我们一般会使用尽可能多的数据去计算估计量或拟合模型，而非总是使用从总体中抽取更多样本的方法。

警告：

区分单个数据点的分布（称为数据分布 data distribution）和样本统计量的分布（称为抽样分布 sampling distribution）非常重要。

通常，样本统计量（如均值等）的分布要比数据本身的分布更加规则，分布的形状更趋向于正态分布的钟形曲线。统计所基于的样本规模越大，上面的观点就愈发成立。此外，样本的规模越大，样本统计量的分布就越窄。

这一点可以通过一个例子说明：使用 LendingClub 贷款申请人的年度收入数据（有关数据说明见第 239 页“小例子：预测贷款违约”）。从这些数据中抽取三个样本：一个包含 1,000 个值的样本，一个包含 1,000 个由 5 个值求得均值的样本，以及一个包含 1,000 个由 20 个值求得均值的样本。然后绘制每个样本的直方图，就得到了图 2-6。

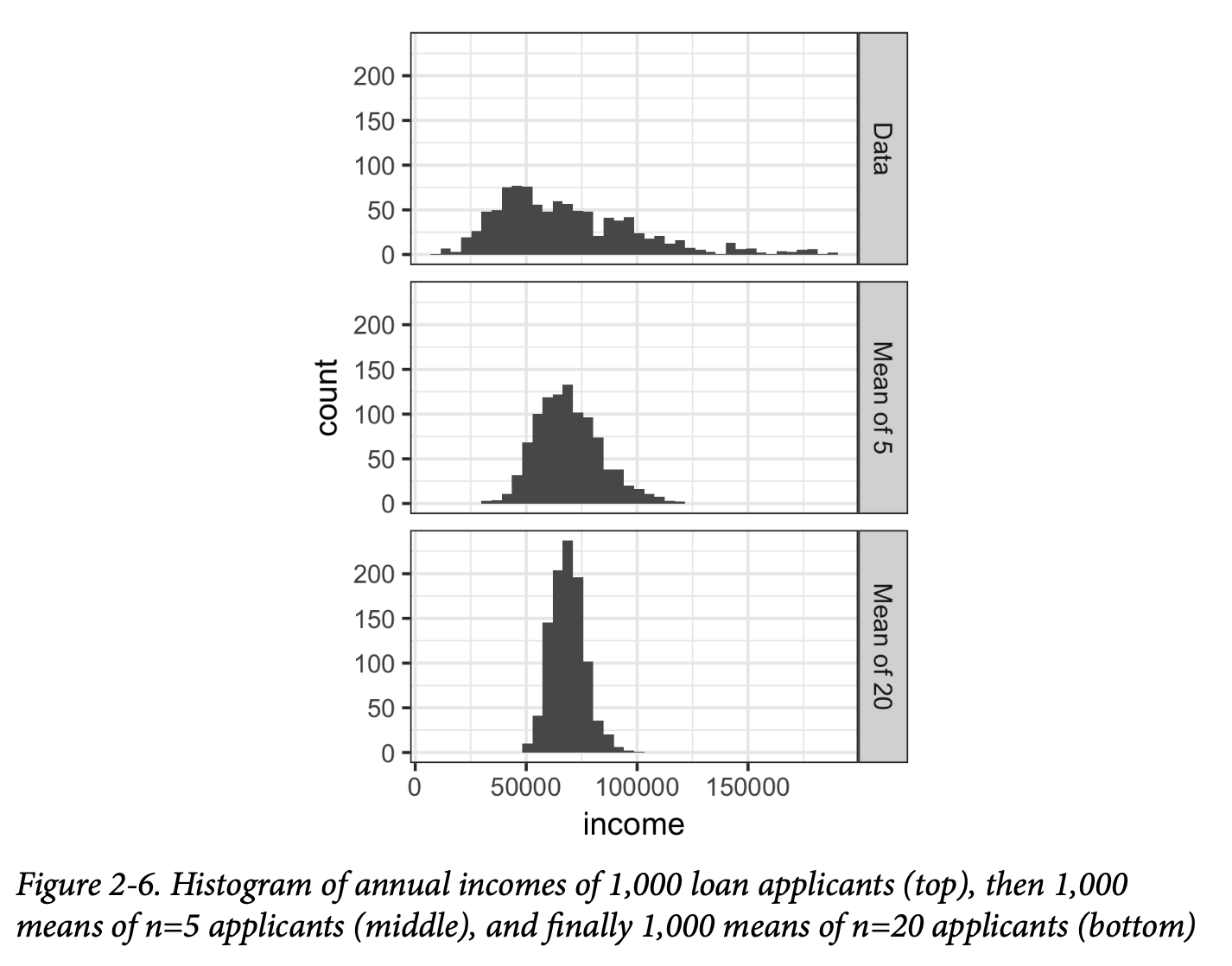
单个数据值的直方图分布得很宽，并且偏向较高的数值，这正是收入数据的常见特征。5 个值和 20 个值的均值的直方图则越来越集中，并且更呈现钟形分布。

下面是使用可视化包 ggplot2 生成这些直方图的 R 代码：

library(ggplot2)
# 抽取一个简单随机样本
samp_data <- data.frame(income=sample(loans_income, 1000),
type='data_dist')
# 抽取5个值的均值样本
samp_mean_05 <- data.frame(
income = tapply(sample(loans_income, 1000*5),
rep(1:1000, rep(5, 1000)), FUN=mean),
type = 'mean_of_5')
# 抽取20个值的均值样本
samp_mean_20 <- data.frame(
income = tapply(sample(loans_income, 1000*20),
rep(1:1000, rep(20, 1000)), FUN=mean),
type = 'mean_of_20')
# 合并数据框并将type转换为因子
income <- rbind(samp_data, samp_mean_05, samp_mean_20)
income$type = factor(income$type,
levels=c('data_dist', 'mean_of_5', 'mean_of_20'),
labels=c('Data', 'Mean of 5', 'Mean of 20'))
# 绘制直方图
ggplot(income, aes(x=income)) +
geom_histogram(bins=40) +
facet_grid(type ~ .)

Python 代码使用 seaborn 的 FacetGrid 显示三个直方图：

import pandas as pd
import seaborn as sns

sample_data = pd.DataFrame({
'income': loans_income.sample(1000),
'type': 'Data',
})

sample_mean_05 = pd.DataFrame({
'income': [loans_income.sample(5).mean() for _ in range(1000)],
'type': 'Mean of 5',
})

sample_mean_20 = pd.DataFrame({
'income': [loans_income.sample(20).mean() for _ in range(1000)],
'type': 'Mean of 20',
})

results = pd.concat([sample_data, sample_mean_05, sample_mean_20])
g = sns.FacetGrid(results, col='type', col_wrap=1, height=2, aspect=2)
g.map(plt.hist, 'income', range=[0, 200000], bins=40)
g.set_axis_labels('Income', 'Count')
g.set_titles('{col_name}')

中心极限定理

我们刚刚描述的现象被称为中心极限定理。它指出，从多个样本抽取得到的均值会近似呈现熟悉的钟形正态曲线（参见第 69 页的“正态分布”），即使源总体并不服从正态分布，只要样本量足够大且数据偏离正态分布的程度不是太大。

中心极限定理使得像 t 分布这样的正态近似公式可以用于计算推断所需的抽样分布——也就是置信区间和假设检验。

中心极限定理在传统统计教材中备受关注，因为它支撑着假设检验和置信区间这类工具的运作机制，而这些工具本身在这类教材中占据了大量篇幅。数据科学家应该意识到这一点；不过，由于形式化的假设检验和置信区间在数据科学中所占比重不大，并且无论如何都可以使用自助法（参见第 61 页的“自助法”），所以中心极限定理在数据科学实践中并没有那么“核心”。

标准误

Standard Error

标准误是一个汇总统计量，它概括了某个统计量的抽样分布中的变异程度。标准误可以用样本值的标准差 \(s\) 和样本量 \(n\) 来估计： \[ \text{标准误} = SE = \frac{s}{\sqrt{n}} \]

随着样本量增加，标准误减小，这对应于图 2-6 中的观察结果。标准误与样本量的关系有时被称为“平方根 n 法则”：若要把标准误降低一半，样本量必须增加四倍。

标准误公式的有效性源自中心极限定理。不过，其实你并不需要依赖中心极限定理也能理解标准误。可以考虑以下估计标准误的方法：

1. 从总体中收集若干个全新的样本；
2. 对每个新样本计算某个统计量（如均值）；
3. 计算步骤 2 中得到的所有统计量的标准差，把它作为标准误的估计值。

在实际中，这种通过收集新样本来估计标准误的方法通常不可行（而且在统计上很浪费）。幸运的是，事实证明并不需要真的抽取全新的样本；你可以使用自助重抽样（bootstrap）。

在现代统计学中，自助法已经成为估计标准误的标准方法。它几乎可以用于任何统计量，而且不依赖于中心极限定理或其他分布假设。

警告

标准差与标准误的区别：不要把标准差（衡量单个数据点的变异性）与标准误**（衡量样本统计量的变异性）混淆。

Standard Deviation Versus Standard Error：Do not confuse standard deviation (which measures the variability of individual data points) with standard error (which measures the variability of a sample metric).

关键要点

• 样本统计量的频率分布告诉我们这个指标在不同样本间可能有多大差异；
• 这种抽样分布可以通过自助法估计，也可以通过依赖中心极限定理的公式估计；
• 概括样本统计量变异性的一个关键指标就是它的标准误。

自助法

Bootstrap

一种简单且有效的方法，可以用来估计某个统计量或模型参数的抽样分布，就是从原始样本本身中有放回地抽取额外样本，并对每个重抽样重新计算统计量或模型。这个过程叫作自助法（bootstrap），它不一定需要假设数据或样本统计量服从正态分布。

自助法的关键术语

• 自助样本（Bootstrap sample）： 从观测数据集中有放回地抽取得到的样本。
• 重抽样（Resampling）： 从观测数据中反复抽取样本的过程；包括自助法和置换（洗牌）等方法。 bootstrap and permutation (shuffling) procedures.

从概念上讲，你可以把自助法想象为把原始样本复制成几千甚至几百万份，从而得到一个“假想总体”，它包含了你原始样本中的所有信息（只是更大了）。然后你可以从这个假想总体中抽取样本，用来估计抽样分布（见图 2-7）。

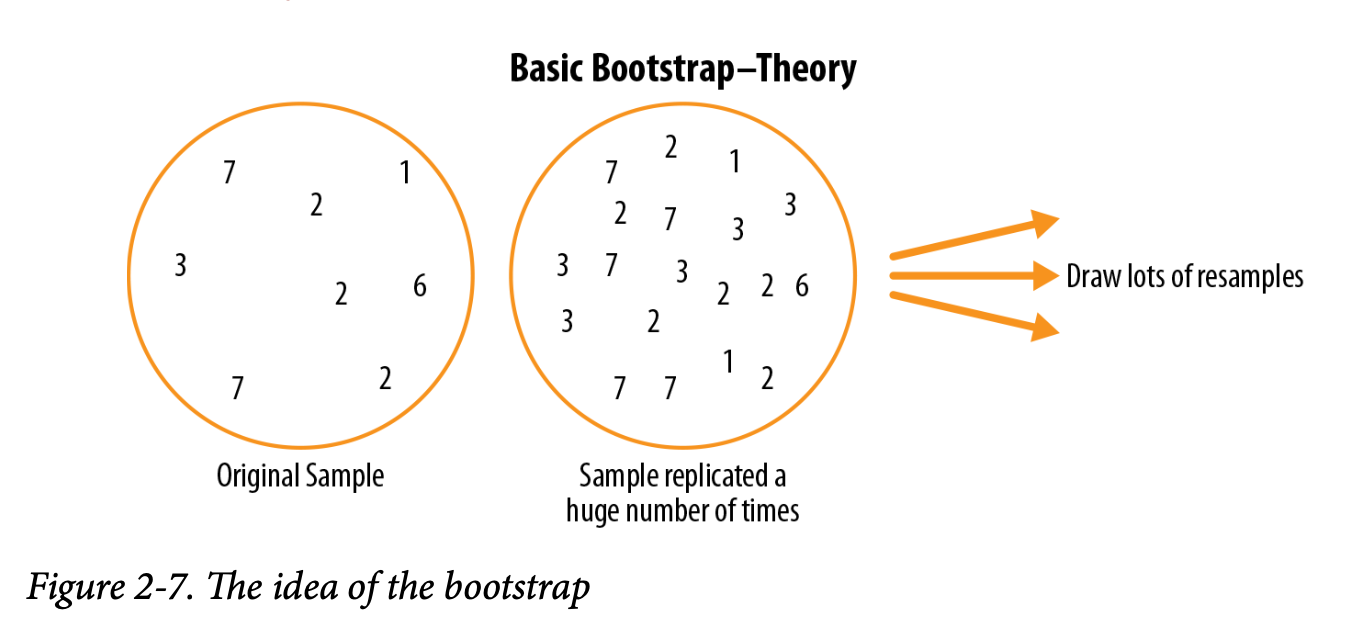
在实践中，并不需要真的把样本复制成巨大的规模。我们只是每抽取一个观测值后再放回，也就是有放回抽样。这样就等效于创建了一个无限总体，其中每个元素在每次抽取时被选中的概率保持不变。

对大小为 n 的样本做均值自助重抽样的算法如下：

1. 抽取一个样本值，记录并放回；

2. 重复上述过程 n 次；

3. 记录这 n 个重抽样值的均值；

4. 重复步骤 1–3 共 R 次；

5. 使用这 R 次的结果来：

   • 计算它们的标准差（估计样本均值的标准误）；
   • 绘制直方图或箱线图；
   • 求出置信区间。

R（自助法迭代次数）是人为设定的。迭代次数越多，标准误或置信区间的估计就越精确。这个过程的结果是一组自助样本统计量或模型参数估计值，你可以据此观察它们的变异性。

R 包 boot 将这些步骤整合到一个函数中。例如，下面把自助法应用于贷款人收入的中位数：

library(boot)
stat_fun <- function(x, idx) median(x[idx])
boot_obj <- boot(loans_income, R=1000, statistic=stat_fun)

函数 stat_fun 会针对索引 idx 指定的样本计算中位数。结果如下：

Bootstrap Statistics :
original bias std. error
t1* 62000 -70.5595 209.1515

中位数的原始估计值是 $62,000。自助分布显示该估计的偏差约为 –$70，标准误为 $209。不同运行之间结果会略有差异。

主要的 Python 包没有直接提供自助法实现。可以用 scikit-learn 的 resample 方法实现：

results = []
for nrepeat in range(1000):
    sample = resample(loans_income)
    results.append(sample.median())
results = pd.Series(results)
print('Bootstrap Statistics:')
print(f'original: {loans_income.median()}')
print(f'bias: {results.mean() - loans_income.median()}')
print(f'std. error: {results.std()}')

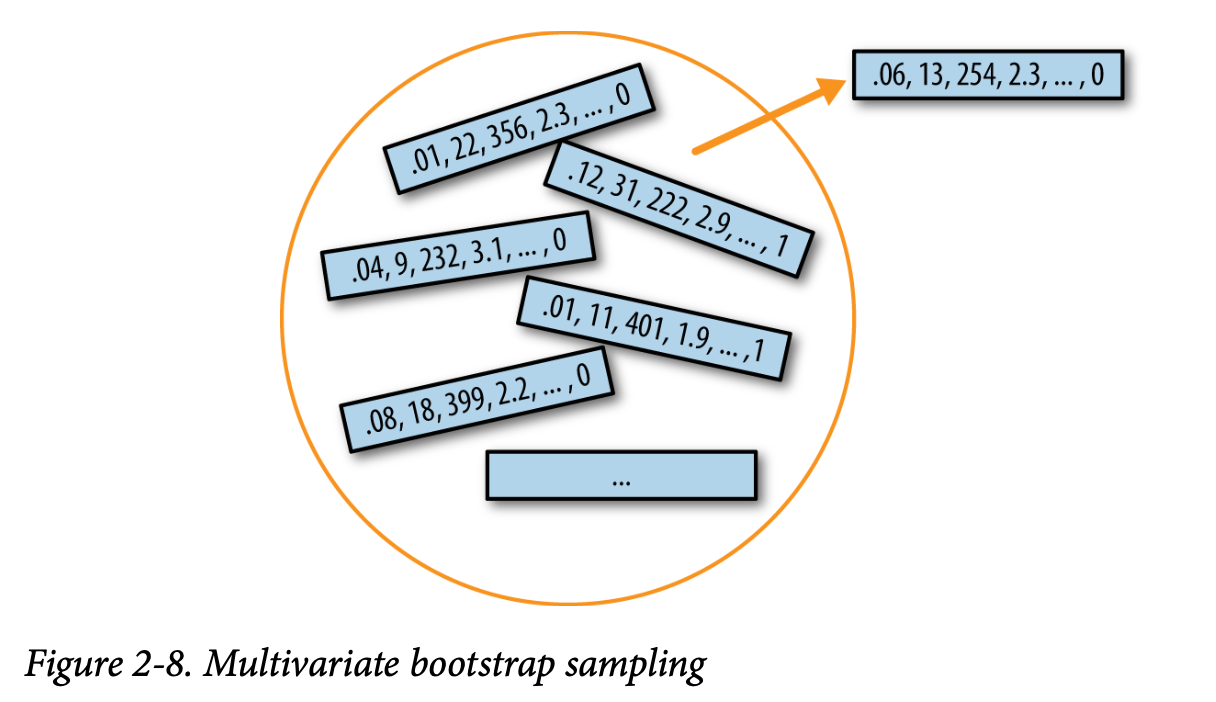
自助法可以用于多变量数据，其中按行作为单元进行抽样（见图 2-8）。然后可以在自助重抽样的数据上运行模型，例如：

• 估计模型参数的稳定性（变异性）；
• 提升预测能力。

对于分类与回归树（decision trees），在自助样本上运行多棵树并对其预测进行平均（分类问题取多数投票）通常比只用一棵树效果更好。这个过程叫作Bagging（“Bootstrap Aggregating”的缩写；参见第 259 页“Bagging 和随机森林”）。

自助法的重复重采样在概念上非常简单，经济学家兼人口学家 Julian Simon 在其 1969 年的著作 Basic Research Methods in Social Science（《社会科学基础研究方法》，Random House）中就收录了包括自助法在内的重采样示例大全。然而，这种方法在计算上非常密集，在计算能力尚未普及之前并不可行。这个技术之所以得名并流行起来，是因为斯坦福大学统计学家 Bradley Efron 在 1970 年代末至 1980 年代初发表了多篇论文和一本书。它在需要用统计方法但并非统计学家的研究者中尤为受欢迎，尤其适用于那些缺乏数学近似方法的度量或模型。平均值的抽样分布自 1908 年以来已得到很好建立，但许多其他度量的抽样分布则没有。自助法还可用于样本量的确定；可以尝试不同的 n 值，观察抽样分布的变化情况。

自助法在首次提出时曾遭到相当多的怀疑，许多人觉得这就像是“把稻草变成黄金”。这种怀疑源于对自助法目的的误解。

警告： 自助法并不能弥补样本量小的问题；它不会创造新数据，也不会填补已有数据集的空白。它只是告诉我们：如果从类似原始样本的总体中抽取大量额外样本，结果会如何表现。

重采样与自助法的区别

Resampling Versus Bootstrapping

有时“重采样”一词被用作“自助法”的同义词，如上所述。但更多时候，“重采样”还包括排列检验（见第 97 页“置换检验”），此时会将多个样本合并，并可能在不放回的情况下进行抽样。无论如何，“自助法”一词始终意味着从观测数据集中进行有放回的抽样。

关键要点

• 自助法（从数据集中有放回抽样）是评估样本统计量变异性的有力工具。
• 自助法可以在各种情境下以类似方式应用，而无需对抽样分布进行大量数学近似研究。
• 它还可以让我们估计那些尚无数学近似公式的统计量的抽样分布。
• 当应用于预测模型时，对多个自助样本的预测结果进行汇总（即“袋装”）通常优于使用单一模型。

置信区间

Confidence Intervals

频数表、直方图、箱线图和标准误差都是理解样本估计潜在误差的手段。置信区间是另一种方法。

置信区间的关键术语

• 置信水平（Confidence level）：按照同样方法从同一总体构造的置信区间中，预计包含目标统计量的比例（百分比）。
• 区间端点（Interval endpoints）：置信区间的上下限。

人类对不确定性有天然的厌恶感；人们（尤其是专家）很少说“我不知道”。分析师和管理者虽然承认不确定性，但当估计值以单一数字（点估计）呈现时，仍会对其抱有过高信任。将估计值呈现为一个区间而非单一数字，是对抗这种倾向的一种方式。置信区间基于统计抽样原理，正是这样做的。

置信区间总是伴随一个覆盖水平，用（较高的）百分比表示，比如 90% 或 95%。一种理解 90% 置信区间的方式是：它是包含该样本统计量自助抽样分布中间 90% 的区间（见第 61 页“自助法”）。更一般地说，一个围绕样本估计的 x% 置信区间，在类似抽样程序下，平均应包含类似的样本估计 x% 的时间。

基于自助法的置信区间算法（样本量 n，关注的统计量）：

1. 从数据中有放回抽取 n 个观测值（重采样）。
2. 记录重采样的统计量。
3. 重复步骤 1–2 多次（R 次）。
4. 对于 x% 的置信区间，从分布两端各裁掉 \((100 - x)/2\)% 的 R 次重采样结果。
5. 剩余区间的端点就是 x% 自助置信区间的端点。

图 2-9 展示了一个贷款申请人年均收入的 90% 置信区间，该样本量为 20，均值为 62,231 美元。

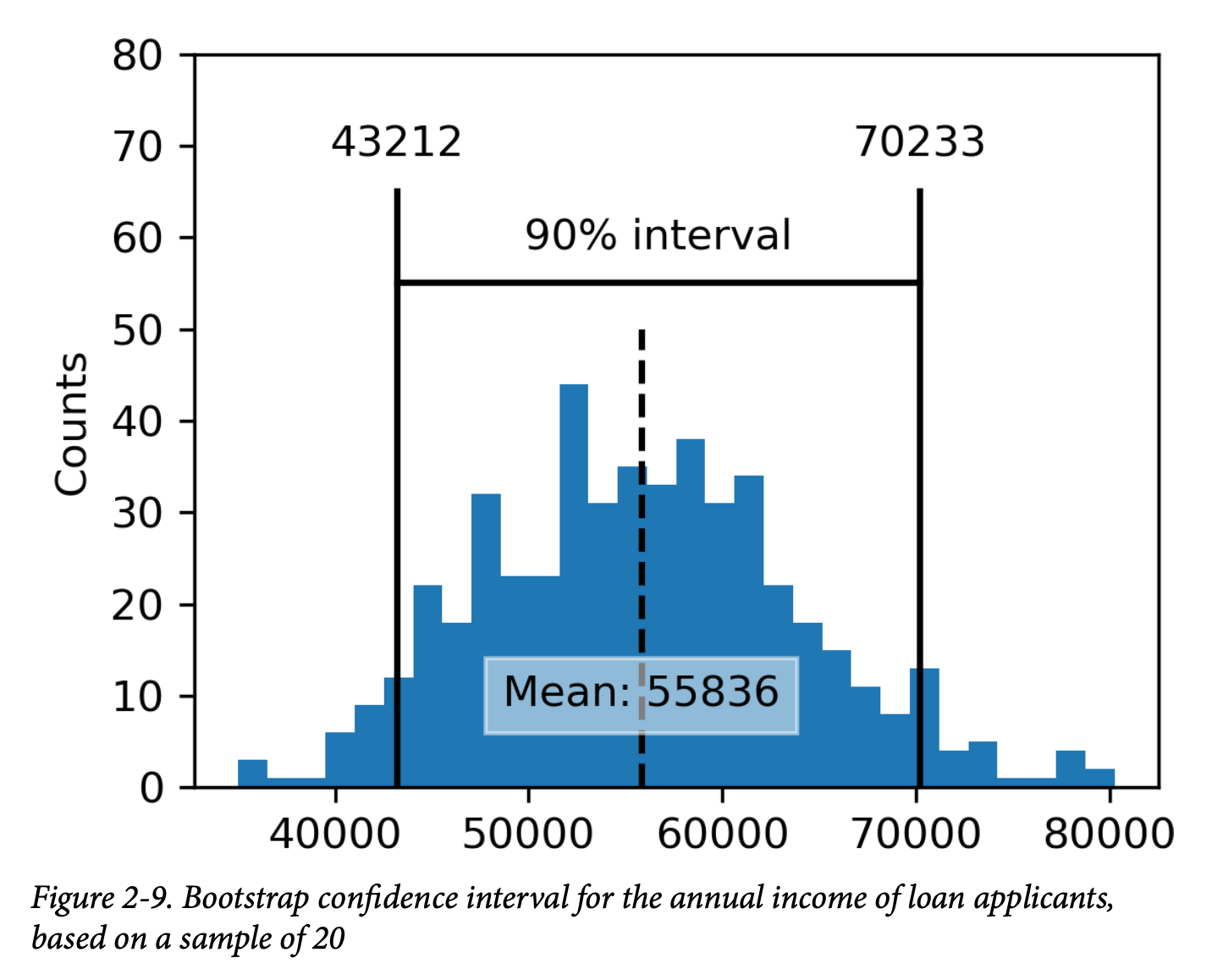
自助法是一种通用工具，可用于为大多数统计量或模型参数生成置信区间。传统的统计教材和软件由于其半个多世纪“无计算机”统计分析的历史，通常还会引用基于公式（尤其是 t 分布，见第 75 页“Student’s t 分布”）生成的置信区间。

通用注解：

当然，当我们得到一个样本结果时，真正想问的问题往往是：“真实值落在某个区间内的概率是多少？”严格来说，这并不是置信区间回答的问题，但这却是大多数人理解置信区间答案的方式。

与置信区间相关的概率问题通常以这样的句子开头：“在给定一个抽样程序和总体的前提下，……的概率是多少？”如果要反向提问——“在给定一个样本结果的情况下，某件关于总体的事情为真的概率是多少？”——则需要更复杂的计算以及更深层次的不可知因素。

与置信区间相关的百分比被称为置信水平。置信水平越高，区间越宽；样本量越小，区间也越宽（即不确定性越大）。两点都符合直觉：你越想要更高的置信度，或者你的数据越少，你就必须使置信区间更宽，才能有足够把握覆盖真实值。

通用注解：

对于数据科学家而言，置信区间是一种帮助理解样本结果可能有多大变动的工具。数据科学家使用这类信息通常不是为了发表学术论文或向监管机构提交结果（如研究人员那样），而更可能是为了传达估计值潜在的误差，或评估是否需要更大的样本量。

关键要点

• 置信区间是把估计值呈现为区间范围的典型方法。
• 数据越多，样本估计值的变动越小。
• 你能容忍的置信水平越低，置信区间就越窄。
• 自助法是构建置信区间的有效方法。

正态分布

钟形的正态分布在传统统计中具有标志性。样本统计量的分布往往呈正态形状，这一事实使得它成为开发逼近这些分布的数学公式的有力工具。

正态分布关键术语

• 误差（Error）：数据点与预测值或平均值之间的差异。
• 标准化（Standardize）：减去均值并除以标准差。
• z 分数（z-score）：单个数据点标准化后的结果。
• 标准正态（Standard normal）：均值 = 0、标准差 = 1 的正态分布。
• QQ 图（QQ-Plot）：用来可视化样本分布与指定分布（如正态分布）接近程度的图形。

在正态分布中（图 2-10），68% 的数据位于均值 ±1 个标准差内，95% 的数据位于均值 ±2 个标准差内。

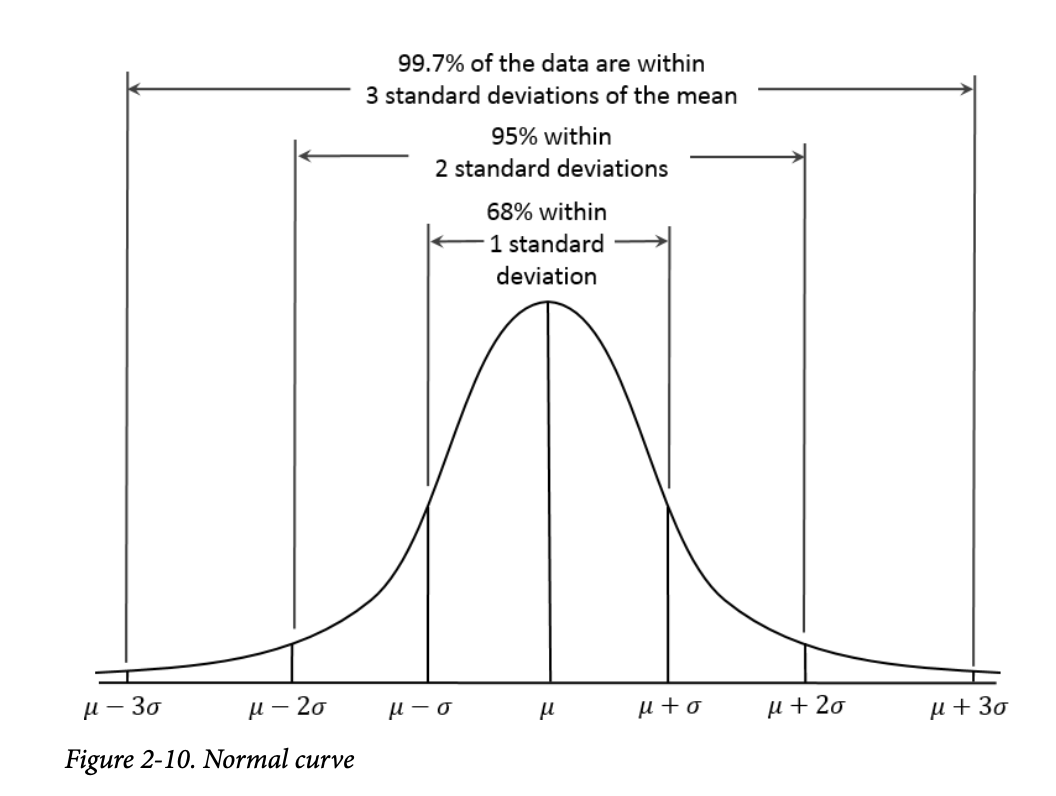
警告：

一个常见的误解是，正态分布之所以叫“normal”，是因为大多数数据都服从正态分布——也就是说它是“正常的”。实际上，大多数典型数据科学项目中使用的变量——事实上绝大多数原始数据——并不服从正态分布（见第 73 页“长尾分布”）。正态分布的真正用途在于，许多统计量在其抽样分布中近似正态分布。即便如此，只有在经验概率分布或自助法分布不可用时，才会使用正态性假设作为最后手段。

通用注解

正态分布（Normal distribution）也被称为高斯分布（Gaussian distribution），名字来源于 18 世纪末、19 世纪初的德国天才数学家卡尔·弗里德里希·高斯（Carl Friedrich Gauss）。 正态分布以前还被称为“误差分布（error distribution）”。在统计学中，误差指的是实际值与统计估计值（如样本均值）之间的差异。例如，标准差（standard deviation）（见第 13 页“变异性的估计”）就是基于数据与其均值之间的误差计算出来的。高斯对正态分布的研究最初源自他对天文观测误差的分析——这些误差被发现服从正态分布。

标准正态分布与 QQ 图

标准正态分布是指横轴单位用“距均值的标准差个数”来表示的正态分布。要将数据与标准正态分布进行比较，需先减去均值，再除以标准差；这一过程也称为标准化（standardization）或正则化（normalization）（见第 243 页“标准化（Normalization，z 分数）”）。注意，这里所说的“标准化”与数据库记录的标准化（转换成统一格式）无关。转换后的值称为 z 分数（z-score），而正态分布有时也称为 z 分布（z-distribution）。

QQ 图（QQ-Plot）用于可视化地判断一个样本是否接近某个指定分布（这里是正态分布）。QQ 图会先按从低到高排列 z 分数，并将每个值的 z 分数绘制在纵轴；横轴则是该值排名对应的正态分布分位数。由于数据已标准化，单位对应的是距均值的标准差个数。如果点大致落在对角线上，那么样本分布就可以认为接近正态分布。

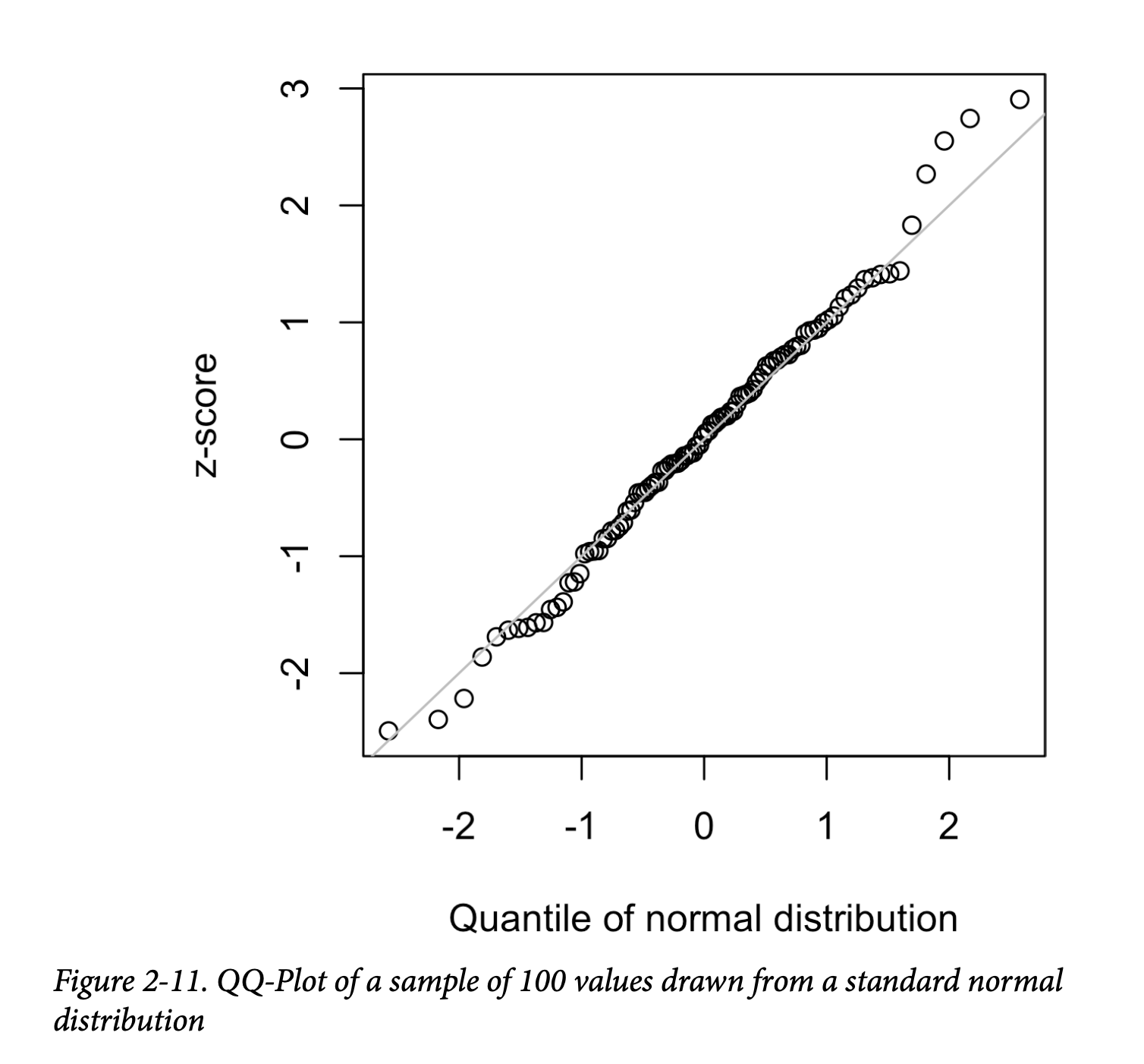
图 2-11 显示了一个从正态分布随机生成的 100 个值的 QQ 图；如预期那样，点紧密跟随直线。 在 R 中可用以下代码生成：

norm_samp <- rnorm(100)
qqnorm(norm_samp)
abline(a=0, b=1, col='grey')

在 Python 中，可以用 scipy.stats.probplot 方法创建 QQ 图：

fig, ax = plt.subplots(figsize=(4, 4))
norm_sample = stats.norm.rvs(size=100)
stats.probplot(norm_sample, plot=ax)

警告

将数据转换为 z 分数（即标准化或正则化）并不会使数据本身服从正态分布**，它只是把数据放到与标准正态分布相同的尺度上，通常用于比较目的。

关键要点

• 正态分布在统计学发展史上至关重要，因为它允许用数学方法近似不确定性和变异性。
• 虽然原始数据通常不是正态分布的，但误差往往是正态分布的，大样本中的平均值和总和也常常是正态分布的。
• 将数据转换为 z 分数的方法：先减去数据的均值，再除以标准差；这样就能把数据与正态分布进行比较。

长尾分布

Long-Tailed Distributions

尽管正态分布在统计学历史上具有重要地位，但与其名字所暗示的相反，数据通常并不是正态分布的。

长尾分布关键术语

尾部（Tail） 频率分布中狭长的部分，其中相对极端的值以低频率出现。

偏斜（Skew） 当分布的一条尾巴比另一条更长时，即为偏斜。

虽然正态分布常常适用于误差和样本统计量的分布，但它通常并不能刻画原始数据的分布。有时，分布高度偏斜（不对称），如收入数据；或者分布是离散的，如二项分布数据。对称和不对称分布都可能具有长尾。分布的尾部对应极端值（小值和大值）。在实际工作中，人们普遍认识到长尾现象及防范其风险。纳西姆·塔勒布提出的“黑天鹅”理论就预测，像股市崩盘这样的异常事件发生的概率远高于正态分布所预测的水平。

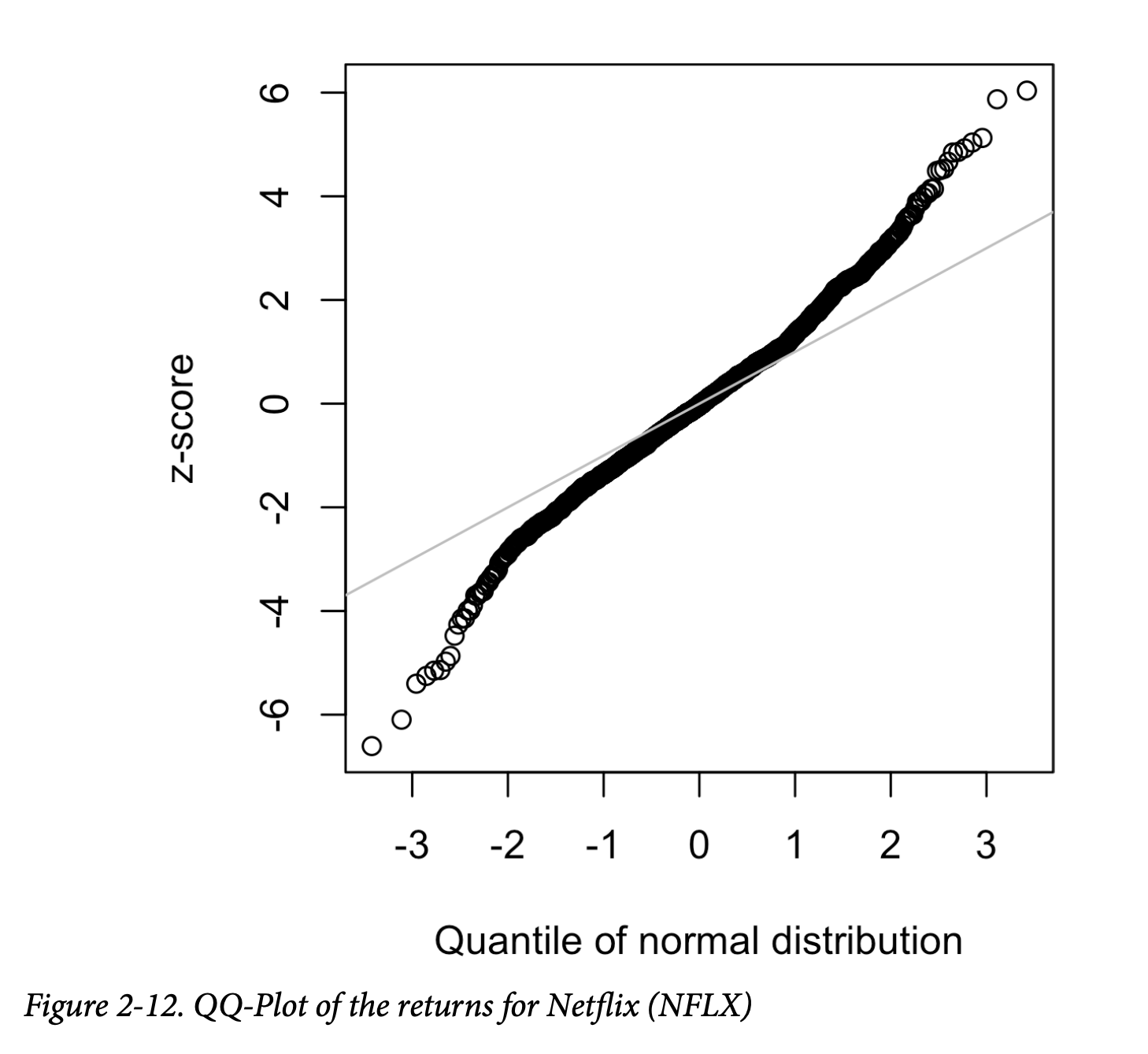
一个说明数据长尾特征的好例子是股票收益率。图 2-12 展示了 Netflix（NFLX）日度股票收益率的 QQ 图。这在 R 中可以这样生成：

nflx <- sp500_px[,'NFLX']
nflx <- diff(log(nflx[nflx>0]))
qqnorm(nflx)
abline(a=0, b=1, col='grey')

对应的 Python 代码为：

nflx = sp500_px.NFLX
nflx = np.diff(np.log(nflx[nflx>0]))
fig, ax = plt.subplots(figsize=(4, 4))
stats.probplot(nflx, plot=ax)

与图 2-11 相比，这些点在低值时远低于直线，在高值时远高于直线，表明数据并非正态分布。这意味着我们比正态分布所预测的更有可能观察到极端值。图 2-12 还展示了另一种常见现象：在均值一个标准差范围内的数据点接近直线。Tukey 将这一现象称为“中间正态”但尾部更长（参见 [Tukey-1987]）。

关于将统计分布拟合到观测数据这一任务，有大量统计学文献。要警惕一种过于数据中心化的方法——这项工作既是科学也是艺术。数据具有变异性，并且表面上往往与不止一种形状和类型的分布一致。通常必须结合领域知识和统计知识，才能确定在某一情境下应使用何种分布进行建模。例如，我们可能有关于某台服务器在许多连续 5 秒时间段内的网络流量数据。此时，了解“每时间段事件数”最合适的分布是泊松分布（参见第 83 页“泊松分布”）就很有用。

关键要点

• 大多数数据并非正态分布。
• 假设正态分布可能导致对极端事件（“黑天鹅”）的低估。

Student’s t 分布

t 分布的形状与正态分布相似，只是尾部稍厚、稍长。它被广泛用于描述样本统计量的分布。样本均值的分布通常呈现出类似 t 分布的形状，并且 t 分布有一个“族”，它们的形状随样本量大小而不同：样本越大，t 分布越接近正态分布。

学生 t 分布的关键术语

\(n\) 样本量。

自由度 一个参数，使 t 分布能够根据不同的样本量、统计量和组数进行调整。

t 分布常被称为 Student’s t 分布，因为它最早由 W. S. Gosset 以“Student”笔名在 1908 年的《Biometrika》上发表。Gosset 当时在健力士（Guinness）啤酒厂工作，雇主不希望竞争对手知道他们正在使用统计方法，因此要求 Gosset 不要用真名发表文章。

Gosset 想回答的问题是：“从总体中抽取一个样本后，样本均值的抽样分布是什么样的？” 他最初通过重抽样实验来探索这一问题：他从包含 3,000 个罪犯身高和左中指长度的数据中，随机抽取大小为 4 的样本。（在当时的优生学背景下，人们对犯罪数据和犯罪倾向与身体或心理特征之间的相关性十分感兴趣。）Gosset 将标准化后的结果（即 z 分数）画在 x 轴上，将频率画在 y 轴上。同时，他推导出一个现在被称为 Student’s t 的函数，并将该函数与样本结果拟合并进行比较（见图 2-13）。

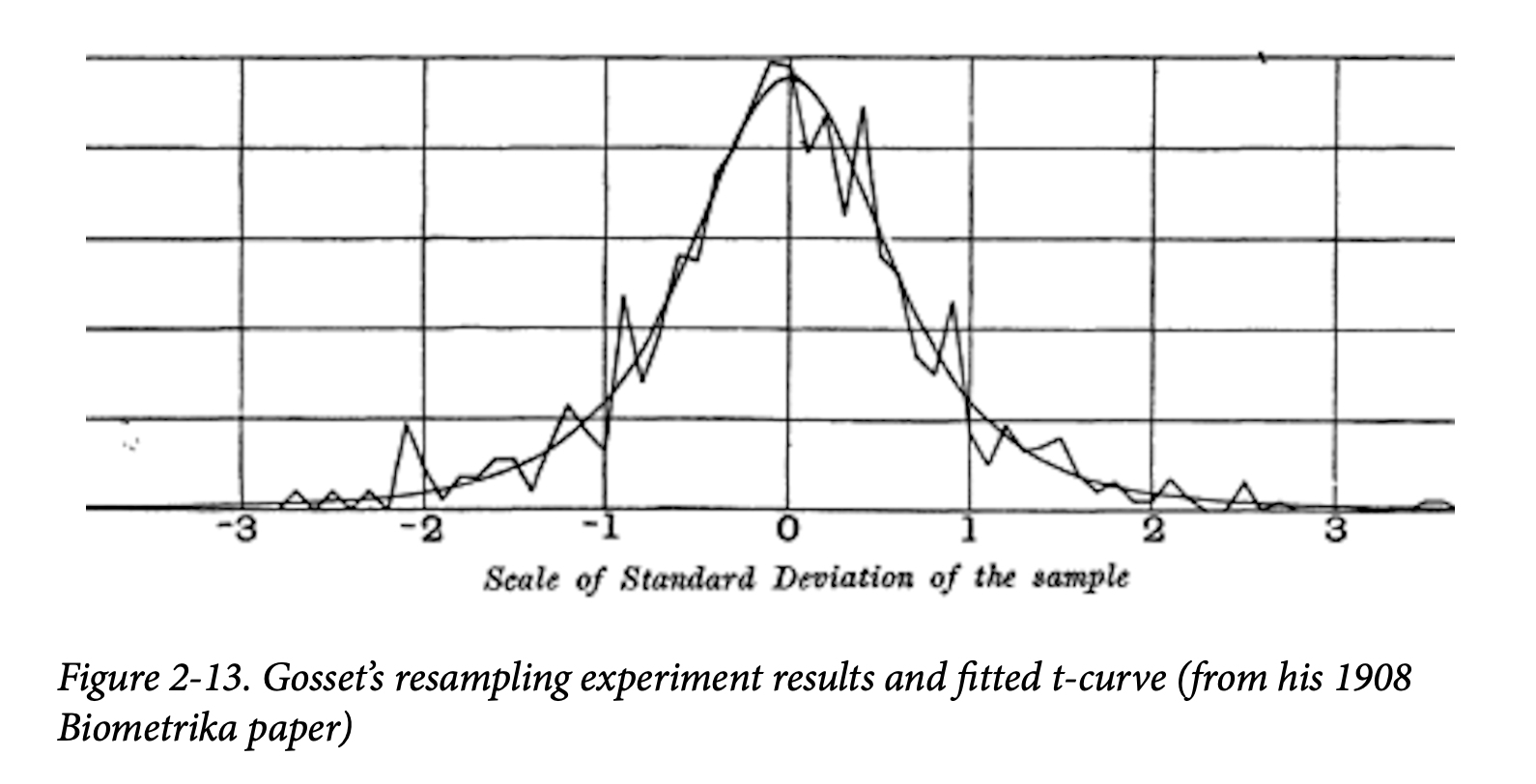
许多不同的统计量在标准化后都可以与 t 分布进行比较，从而在考虑抽样变异的情况下估计置信区间。设样本量为 \(n\)，样本均值为 \(\bar{x}\)，样本标准差为 \(s\)。则样本均值的 90% 置信区间为：

\[ \bar{x} \pm t_{n-1}(0.05)\frac{s}{\sqrt{n}} \]

其中 \(t_{n-1}(0.05)\) 是具有 \(n-1\) 个自由度（见第 116 页“自由度”部分）且在两端各“切掉”5% 的 t 统计量值。t 分布可作为参考来描述样本均值、两个样本均值之差、回归参数以及其他统计量的分布。

如果 1908 年就已经普及强大的计算能力，那么统计学无疑会从一开始就更多地依赖计算量密集的重抽样方法。由于当时没有计算机，统计学家们转向数学与诸如 t 分布这样的函数来近似抽样分布。到了 1980 年代，计算能力使得实际的重抽样实验成为可能，但那时 t 分布等方法已经在教材和软件中根深蒂固。

t 分布能够准确描述样本统计量的前提，是该统计量在样本中的分布近似正态分布。事实证明，即使总体数据本身并不服从正态分布，样本统计量往往仍近似正态分布（这一事实促使 t 分布被广泛应用）。这又回到了一个现象——中心极限定理（见第 60 页“中心极限定理”）。

通用注解： 数据科学家需要了解 t 分布和中心极限定理的哪些内容？其实不用太多。t 分布用于经典统计推断，但对数据科学的核心目的来说并非那么重要。理解和量化不确定性与变异性对数据科学家来说很重要，但经验性自助（bootstrap）抽样可以回答大多数关于抽样误差的问题。不过，数据科学家在统计软件和 R 的统计过程输出中会经常遇到 t 统计量——例如在 A/B 测试和回归分析中——因此了解它的用途还是有帮助的。

关键要点

• t 分布实际上是一族分布，它们看起来像正态分布，但尾部更厚。
• t 分布被广泛用作样本均值分布、两个样本均值之差、回归参数等分布的参考基础。

二项分布

Binomial Distribution

是/否（二项）结果处于分析的核心，因为它们通常是决策或其他过程的最终结果：购买/不购买、点击/不点击、生存/死亡等等。理解二项分布的核心是“试验集合”的概念：每次试验有两个可能的结果，并且每个结果的概率是确定的。

例如，掷硬币 10 次就是一个包含 10 次试验的二项试验，每次试验有两个可能的结果（正面或反面）；见图 2-14。此类是/否或 0/1 的结果称为二元结果，它们不一定是 50/50 的概率。只要概率之和为 1.0，就都是可能的。在统计学中，习惯上称“1”这个结果为“成功”结果；也常将“1”分配给较少见的结果。“成功”一词并不意味着结果是可取的或有益的，而只是指感兴趣的结果。例如，贷款违约或欺诈交易是我们可能感兴趣预测的相对少见事件，因此它们被称为“1”或“成功”。

二项分布的关键术语

• 试验（Trial） 一个具有离散结果的事件（例如抛硬币）。

• 成功（Success） 试验中关注的结果。 同义词： “1”（相对于“0”）

• 二项（Binomial） 具有两个结果。 同义词： 是/否（yes/no）、0/1、二元（binary）

• 二项试验（Binomial trial） 具有两种结果的试验。 同义词：伯努利试验（Bernoulli trial）

• 二项分布（Binomial distribution） 在 \(x\) 次试验中成功次数的分布。 同义词：伯努利分布（Bernoulli distribution）

二项分布就是在给定试验次数 \(n\) 和每次试验成功概率 \(p\) 的条件下，成功次数 \(x\) 的频率分布。根据 \(n\) 和 \(p\) 的不同，有一族二项分布。二项分布能回答这样的问题：

如果点击转化为购买的概率是 0.02，那么在 200 次点击中观察到 0 次购买的概率是多少？

R 函数 dbinom 用来计算二项概率。例如：

dbinom(x=2, size=5, p=0.1)

会返回 0.0729，即在 5 次试验中，每次试验成功概率 \(p=0.1\) 时，恰好观察到 \(x=2\) 次成功的概率。对于上面的例子，我们用 \(x=0\)、size=200 和 \(p=0.02\)。用这些参数，dbinom 返回的概率是 0.0176。

我们经常还想知道在 \(n\) 次试验中，\(x\) 次或更少成功的概率。这时使用函数 pbinom：

pbinom(2, 5, 0.1)

它会返回 0.9914，即在 5 次试验中，每次试验成功概率 0.1 时，观察到 2 次或更少成功的概率。

scipy.stats 模块实现了大量统计分布。对于二项分布，可以使用函数 stats.binom.pmf 和 stats.binom.cdf：

stats.binom.pmf(2, n=5, p=0.1)
stats.binom.cdf(2, n=5, p=0.1)

二项分布的均值是 \(n \times p\)；也可以将其看作 \(n\) 次试验中预期的成功次数（成功概率 = \(p\)）。 方差是 \(n \times p (1-p)\)。当试验次数足够大（尤其是当 \(p\) 接近 0.50 时），二项分布几乎与正态分布无法区分。实际上，在大样本情况下计算二项概率计算量很大，因此大多数统计过程会用正态分布（用均值和方差）进行近似。

关键要点

• 建模二项结果非常重要，因为它们代表了许多基本决策（如购买或不购买、点击或不点击、生存或死亡等）。
• 二项试验是一个有两种可能结果的实验：一种的概率为 \(p\)，另一种的概率为 \(1 - p\)。
• 当 \(n\) 很大且 \(p\) 不太接近 0 或 1 时，二项分布可以用正态分布近似。

卡方分布

Chi-Square Distribution

在统计学中，一个重要的思想是“偏离期望”，尤其是针对类别计数而言。这里“期望”可粗略地定义为“数据中没有什么异常或值得注意的现象”（例如变量之间没有相关性或可预测的模式）。这也被称为“原假设”或“零模型”（参见第94页“原假设”）。

例如，你可能想要检验一个变量（比如表示性别的行变量）是否独立于另一个变量（比如表示“是否在工作中获得晋升”的列变量），并且你手头有每个数据表单元格中的人数计数。衡量结果偏离独立性原假设期望程度的统计量就是卡方统计量。它的计算方法是：观察值与期望值之差，除以期望值的平方根，再平方，然后对所有类别求和。这个过程对统计量进行了标准化，使其可以与参考分布进行比较。更一般地说，卡方统计量衡量的是一组观测值与某一指定分布“拟合”的程度（即“拟合优度”检验）。它对于确定多种处理（“A/B/C…测试”）的效果是否彼此不同非常有用。

卡方分布就是在从零模型中反复抽样时，这个统计量的分布——详细算法见第124页“卡方检验”及数据表的卡方公式。一组计数的卡方值低，表示它们与期望分布非常接近；卡方值高，则表示它们与期望差异明显。与不同自由度（例如观测数——见第116页“自由度”）相关的卡方分布有多种。

关键要点

• 卡方分布通常关注的是落入不同类别中的个体或项目的计数。
• 卡方统计量衡量的是数据相对于零模型期望的偏离程度。

F 分布

F-Distribution

在科学实验中，一个常见的做法是跨不同组测试多种处理——例如，在田地不同区块上使用不同的肥料。这与卡方分布中提到的 A/B/C 测试（见第 80 页“卡方分布”）类似，但我们这里处理的是连续测量值，而不是计数值。在这种情况下，我们关注的是组间均值差异是否大于在正常随机波动下可能预期的程度。F 统计量衡量的就是这一点，它是组间均值变异性与组内变异性（也称为残差变异性）的比值。这种比较称为方差分析(analysis of variance)（见第 118 页“ANOVA”）。F 统计量的分布是对在所有组均值相等（即零假设模型）的数据进行随机置换所产生的所有可能值的频率分布。不同自由度（例如组数——见第 116 页“自由度”）会对应不同的 F 分布。F 的计算在 ANOVA 一节中有详细说明。在线性回归中，F 统计量还用于比较回归模型解释的变异与数据总体变异。R 和 Python 在回归和 ANOVA 的例程中会自动生成 F 统计量。

关键概念

• F 分布用于涉及测量数据的实验和线性模型。
• F 统计量比较感兴趣因素造成的变异与总体变异的大小。

泊松分布及相关分布

Poisson and Related Distributions

许多过程在某个总体速率下随机产生事件——例如，网站访客到达（随时间分布的事件）、收费站汽车到达（随时间分布的事件）；每平方米布料中的瑕疵、每 100 行代码中的错别字（随空间分布的事件）。

泊松及相关分布的关键术语

• λ（Lambda） 事件在单位时间或单位空间发生的速率。

• 泊松分布（Poisson distribution） 抽样单位时间或空间内事件数量的频率分布。

• 指数分布（Exponential distribution） 从一个事件到下一个事件的时间或距离的频率分布。

• 威布尔分布（Weibull distribution） 指数分布的广义版本，事件发生速率允许随时间变化。

泊松分布

从先前的总体数据（例如每年的流感感染数）可以估计单位时间或单位空间内事件的平均数（例如每天或每个人口普查单元的感染数）。我们也可能想知道从一个时间/空间单位到另一个时间/空间单位，这个数可能有多大差异。泊松分布告诉我们，当抽取多个这样的单位时，每个单位时间或空间内事件数的分布情况。它在排队问题中很有用，比如：“我们需要多大容量才能在任意五秒内有 95% 的把握完全处理服务器上到达的网络流量？”

泊松分布的关键参数是 λ（lambda）。这是在指定时间或空间区间内发生事件的平均数。泊松分布的方差也是 λ。

一个常见的技巧是在排队模拟中生成来自泊松分布的随机数。R 中的 rpois 函数就是这样做的，它只需要两个参数——随机数数量和 λ：

rpois(100, lambda=2)

对应的 Python 函数是 stats.poisson.rvs：

stats.poisson.rvs(2, size=100)

这段代码会从 λ = 2 的泊松分布中生成 100 个随机数。例如，如果平均每分钟有两个客服电话进来，这段代码就模拟了 100 分钟，每分钟返回呼叫数。

指数分布

使用和泊松分布相同的参数 λ，我们也可以建模事件间隔的分布：如两次访问网站之间的时间，或两辆车到达收费站之间的时间。指数分布还用于工程领域建模失效时间，在流程管理中建模每个服务调用所需时间等。

R 中生成指数分布随机数的代码需要两个参数：

• n（生成的随机数个数）
• rate（每个时间段的事件数）

例如：

rexp(n=100, rate=0.2)

在 Python 的 stats.expon.rvs 中，参数顺序相反：

stats.expon.rvs(0.2, size=100)

这段代码会从平均每时间段 0.2 次事件的指数分布中生成 100 个随机数。你可以用它来模拟 100 个服务电话之间的间隔（单位：分钟），其中平均呼叫速率为每分钟 0.2 次。

对于泊松分布或指数分布的任何模拟研究，一个关键假设是速率 λ 在所考虑的期间内保持不变。总体上这一假设很少完全成立，例如，道路或数据网络的流量会因时段和星期几而变化。然而，通常可以把时间段或空间区域划分为足够同质的小段，以便在这些小段内进行分析或模拟是合理的。

估计失效率

在许多应用中，事件速率 λ 是已知的，或者可以从先前数据中估计。然而，对于罕见事件，情况就不一定如此。例如，飞机发动机失效（幸好）非常罕见，对于某种特定型号的发动机，可能几乎没有数据来估计故障间隔时间。在完全没有数据的情况下，几乎没有依据去估计事件速率。

不过，你可以做一些推测：如果在 20 小时后还没有出现任何事件，你几乎可以肯定速率不是“每小时 1 次”。通过模拟或直接计算概率，你可以评估不同的假设事件速率，并估算速率极不可能低于的阈值。如果有一些数据，但不足以提供精确、可靠的速率估计，就可以对不同速率应用拟合优度检验（参见第 124 页的“卡方检验”），以判断这些速率与观测数据的拟合程度。

威布尔分布

Weibull Distribution

在许多情况下，事件速率并不随时间保持不变。如果速率变化的周期远大于典型事件间隔，就没有问题；只要把分析划分为速率相对恒定的时间段即可（前面提到过）。但是，如果在事件间隔期间速率就发生变化，那么指数分布（或泊松分布）就不再适用。这在机械故障中很常见——随着时间推移，失效风险增加。

威布尔分布是指数分布的推广版本，它允许事件速率随时间变化，并通过形状参数 β来指定：

• 如果 β > 1，事件发生的概率随时间增加；
• 如果 β < 1，事件发生的概率随时间减少。

由于威布尔分布用于“失效时间分析”而不是事件速率分析，它的第二个参数不是每时间段的事件速率，而是用特征寿命（characteristic life）来表示。符号为 η（希腊字母 eta），也叫尺度参数（scale parameter）。

对于威布尔分布，估计任务现在包括估计两个参数 β 和 η。通常通过软件对数据建模，得到最合适的威布尔分布估计。

R 语言生成威布尔分布随机数的函数 rweibull 需要三个参数：

• n：生成随机数的个数
• shape：形状参数
• scale：尺度参数（特征寿命）

例如，以下代码从形状参数 1.5、特征寿命 5,000 的威布尔分布中生成 100 个随机数（寿命）：

rweibull(100, 1.5, 5000)

Python 中可用 stats.weibull_min.rvs 实现同样的功能：

stats.weibull_min.rvs(1.5, scale=5000, size=100)

关键要点

• 对于以恒定速率发生的事件，单位时间或单位空间内事件数可以建模为泊松分布。
• 你也可以用指数分布来建模从一个事件到下一个事件的时间或距离。
• 对于随时间变化的事件速率（如设备失效概率随时间增加），可以用威布尔分布建模。

总结

在大数据时代，当需要精确估计时，随机抽样的原则依然重要。随机选择数据可以减少偏差，比单纯使用方便取得的数据集得到更高质量的数据。掌握不同抽样和数据生成分布的知识，可以帮助我们量化估计中由于随机变化可能产生的误差。

同时，自助法（bootstrap）——即从观测数据集中有放回抽样——是一种非常有吸引力的“通用”方法，用于评估样本估计的可能误差。