第1章 探索性数据分析

发表于 分类于

《Practical Statistics for Data Scientists》书籍英文版
《面向数据科学家的实用统计学》中文版书籍

前言

本书旨在帮助对 R 和/或 Python 编程语言有一定熟悉度、并对统计学有过一些前期（可能零星或短暂的）接触的数据科学家。两位作者从统计学领域进入数据科学世界，对统计学能为数据科学这门艺术所做的贡献心怀感激。与此同时，我们深知传统统计学教学的局限性：统计学作为一门学科已有一个半世纪的历史，大多数统计学教科书和课程都承载着巨轮般的动量和惯性。本书中的所有方法都与统计学这门学科有着某种联系——无论是历史上的还是方法论上的。那些主要从计算机科学演变而来的方法，比如神经网络，则不包括在内。

本书的两个目标是：

  • 以易于消化、导航和参考的形式，列出与数据科学相关的关键统计概念。
  • 从数据科学的角度解释哪些概念是重要且有用的，哪些则不那么重要，以及原因何在。

本书使用的约定

本书使用以下排版约定：

  • 斜体（Italic） 表示新术语、URL、电子邮件地址、文件名和文件扩展名。
  • 等宽字体（Constant width） 用于程序列表，以及在段落中引用程序元素，如变量或函数名、数据库、数据类型、环境变量、语句和关键字。
  • 粗体等宽字体（Constant width bold） 显示应由用户按字面键入的命令或其他文本。

关键术语

数据科学是多个学科的融合，包括统计学、计算机科学、信息技术和特定领域。因此，可以使用几个不同的术语来指代同一个概念。关键术语及其同义词将在本书中通过如下所示的侧边栏进行突出显示。

  • 这个元素表示提示或建议。
  • 这个元素表示一般性注释。
  • 这个元素表示警告或注意事项。

使用代码示例

在所有情况下，本书都先给出 R 语言的代码示例，然后是 Python。为了避免不必要的重复，我们通常只展示由 R 代码产生的输出和图表。我们还省略了加载所需包和数据集的代码。您可以在 https://github.com/gedeck/practical-statistics-for-data-scientists 下载完整的代码和数据集。

本书旨在帮助您完成工作。通常，如果本书提供了示例代码，您可以在您的程序和文档中使用它。除非您要复制很大一部分代码，否则无需联系我们获得许可。例如，编写一个使用本书中几个代码片段的程序不需要许可。但销售或分发来自 O'Reilly 书籍的示例需要许可。通过引用本书并引用示例代码来回答问题不需要许可。将本书中的大量示例代码整合到您的产品文档中则需要许可。

我们感激您的署名，但并非强制要求。署名通常包括书名、作者、出版商和 ISBN。例如：“《Practical Statistics for Data Scientists》由 Peter Bruce、Andrew Bruce 和 Peter Gedeck（O'Reilly）著。版权所有 2020 Peter Bruce、Andrew Bruce 和 Peter Gedeck，978-1-492-07294-2。”

如果您觉得您对代码示例的使用超出了合理使用或上述许可范围，请随时通过 permissions@oreilly.com 联系我们。

O’Reilly 在线学习

40多年来，O’Reilly Media 一直提供技术和商业培训、知识和见解，以帮助公司取得成功。

我们独特的专家和创新者网络通过书籍、文章和我们的在线学习平台分享他们的知识和专长。O’Reilly 的在线学习平台为您提供按需访问的直播培训课程、深入的学习路径、交互式编码环境以及来自 O’Reilly 和200多家其他出版商的大量文本和视频。欲了解更多信息，请访问 http://oreilly.com。

如何联系我们

有关本书的意见和问题，请联系出版商：

O’Reilly Media, Inc. 1005 Gravenstein Highway North Sebastopol, CA 95472 800-998-9938（美国或加拿大境内） 707-829-0515（国际或本地） 707-829-0104（传真）

我们为本书设立了一个网页，其中列出了勘误表、示例和任何其他信息。您可以在 https://oreil.ly/practicalStats_dataSci_2e 访问该页面。

发送电子邮件至 bookquestions@oreilly.com，对本书发表评论或提出技术问题。

如需了解有关我们书籍和课程的新闻及更多信息，请访问我们的网站 http://oreilly.com。

在 Facebook 上找到我们：http://facebook.com/oreilly 在 Twitter 上关注我们：http://twitter.com/oreillymedia 在 YouTube 上观看我们：http://www.youtube.com/oreillymedia

致谢

作者们感谢许多帮助本书成为现实的人。

数据挖掘公司 Elder Research 的首席执行官 Gerhard Pilcher 审阅了本书的早期草稿，并给予了我们详细而有益的修正和评论。同样，SAS 的统计学家 Anya McGuirk 和 Wei Xiao，以及 O’Reilly 的作者同事 Jay Hilfiger，也对本书的初稿提供了有益的反馈。将第一版翻译成日文的 Toshiaki Kurokawa 在此过程中进行了全面的审阅和纠正。Aaron Schumacher 和 Walter Paczkowski 全面审阅了本书的第二版，并提供了许多有益和宝贵的建议，我们对此表示由衷的感谢。毋庸置疑，任何遗留的错误都由我们独自承担。

在 O’Reilly，Shannon Cutt 以愉悦的心情和恰当的催促引导我们完成了出版过程，而 Kristen Brown 则顺利地将我们的书带入了制作阶段。Rachel Monaghan 和 Eliahu Sussman 小心翼翼、耐心细致地纠正和改进了我们的写作，而 Ellen Troutman-Zaig 则负责编制了索引。Nicole Tache 负责了第二版的编辑工作，她不仅有效地指导了整个过程，还提供了许多优秀的编辑建议，以提高本书对广大读者的可读性。我们还要感谢 Marie Beaugureau，她在 O’Reilly 发起了我们的项目，以及 Ben Bengfort，O’Reilly 的作者和 Statistics.com 的讲师，是他将我们介绍给了 O’Reilly。

我们和本书也受益于 Peter 多年来与 Galit Shmueli（另一本图书项目的合著者）进行的多次交谈。

最后，我们特别感谢 Elizabeth Bruce 和 Deborah Donnell，她们的耐心和支持使这项工作成为可能。

第1章 探索性数据分析

Exploratory Data Analysis

本章重点介绍任何数据科学项目的第一步：探索数据。

经典的统计学几乎完全专注于推论（inference），这是一套有时很复杂的程序，用于基于小样本对大总体得出结论。1962年，John W. Tukey（图1-1）在他那篇开创性论文《数据分析的未来》[Tukey-1962]中呼吁对统计学进行改革。他提出了一门名为数据分析的新科学学科，其中统计推论仅作为其一个组成部分。Tukey 与工程和计算机科学界建立了联系（他创造了bit，即binary digit的缩写，以及 software 等术语），他的原始原则出人意料地持久，并构成了数据科学的基础之一。1977年，Tukey 凭借其如今已成为经典的著作《探索性数据分析》[Tukey-1977]奠定了探索性数据分析这一领域。Tukey 提出了简单的图表（例如，箱线图、散点图），这些图表与汇总统计量（均值、中位数、分位数等）一起，有助于描绘数据集的画面。

F1.1

随着计算能力和富有表现力的数据分析软件的普及，探索性数据分析已经远远超出了其最初的范围。推动这一学科发展的关键因素是新技术的快速发展、获取更多和更大数据的能力以及在各种学科中更广泛地使用定量分析。斯坦福大学统计学教授、Tukey 的前本科生 David Donoho，根据他在新泽西州普林斯顿举行的 Tukey 百年纪念研讨会上的演讲撰写了一篇出色的文章 [Donoho-2015]。Donoho 将数据科学的起源追溯到 Tukey 在数据分析方面的开创性工作。

结构化数据的元素

Elements of Structured Data

数据来自许多来源：传感器测量、事件、文本、图像和视频。物联网（IoT）正在喷涌出信息流。这些数据中的大部分是非结构化的：图像是像素的集合，每个像素都包含 RGB（红、绿、蓝）颜色信息。文本是单词和非单词字符的序列，通常按章节、小节等组织。点击流是用户与应用程序或网页交互时的一系列动作。事实上，数据科学的一个主要挑战就是将这种原始数据的洪流转化为可操作的信息。为了应用本书涵盖的统计概念，必须对非结构化的原始数据进行处理和操作，使其成为结构化形式。结构化数据最常见的形式之一是带有行和列的表格——就像可能从关系数据库中出现或为研究而收集的数据一样。

结构化数据有两种基本类型：数值型和类别型。数值型数据有两种形式：连续型，例如风速或持续时间；离散型，例如事件发生的次数。类别型数据只取一个固定的值集，例如电视屏幕的类型（等离子、LCD、LED等）或州名（阿拉巴马州、阿拉斯加州等）。二元数据是类别型数据的一个重要特例，它只取两个值中的一个，例如0/1、是/否或真/假。另一种有用的类别型数据是有序数据（ordinal data），其中的类别是有序的；一个例子是数值评级（1、2、3、4或5）。

我们为什么要费心对数据类型进行分类呢？事实证明，出于数据分析和预测建模的目的，数据类型对于帮助确定视觉显示、数据分析或统计模型的类型非常重要。事实上，R 和 Python 等数据科学软件利用这些数据类型来提高计算性能。更重要的是，变量的数据类型决定了软件将如何处理该变量的计算。

数据类型的关键术语

  • 数值型（Numeric） 在数值尺度上表达的数据。
  • 连续型（Continuous） 可以在一个区间内取任意值的数据。（同义词：interval（区间）、float（浮点））
  • 离散型（Discrete） 只能取整数值的数据，例如计数。（同义词：integer（整数）、count（计数））
  • 类别型（Categorical） 只能取一组代表可能类别的特定值的数据。（同义词：enums（枚举）、enumerated（枚举）、factors（因子）、nominal（名义））
  • 二元型（Binary） 类别型数据的一个特例，只有两个类别的值，例如 0/1、真/假。（同义词：dichotomous（二分）、logical（逻辑）、indicator（指示符）、boolean（布尔））
  • 有序型（Ordinal） 具有明确排序的类别型数据。（同义词：ordered factor（有序因子））

软件工程师和数据库程序员可能会想，我们为什么还需要为分析引入类别型和有序型数据的概念。毕竟，类别仅仅是文本（或数值）值的集合，底层数据库会自动处理其内部表示。然而，将数据明确标识为类别型（与文本区分开来）确实提供了一些优势：

  • 知道数据是类别型可以作为一个信号，告诉软件如何执行统计过程，例如生成图表或拟合模型。特别是，有序数据在 R 中可以表示为 ordered.factor，在图表、表格和模型中保留用户指定的顺序。在 Python 中，scikit-learn 通过 sklearn.preprocessing.OrdinalEncoder 支持有序数据。
  • 存储和索引可以得到优化（如在关系数据库中）。
  • 给定类别变量可能取的值被强制在软件中（类似于枚举 enum）。

第三个“好处”可能会导致意外或意料之外的行为：R 中数据导入函数（例如 read.csv）的默认行为是自动将文本列转换为因子 factor。之后对该列的操作将假定该列唯一允许的值是最初导入的值，并且分配一个新的文本值将引发警告并产生一个 NA（缺失值）。Python 中的 pandas 包不会自动进行这种转换。但是，您可以在 read_csv 函数中显式指定一个列为类别型。

关键思想

  • 在软件中，数据通常按类型进行分类。
  • 数据类型包括数值型（连续型、离散型）和类别型（二元型、有序型）。
  • 软件中的数据类型作为一个信号，告诉软件如何处理数据。

矩形数据

Rectangular Data

在数据科学中，典型的分析参考框架是一个矩形数据对象，就像电子表格或数据库表一样。

矩形数据是一个通用术语，指代一个二维矩阵，其中行表示记录（案例），列表示特征（变量）；数据框（data frame）是 R 和 Python 中特有的格式。数据并非总是以这种形式开始：非结构化数据（例如文本）必须经过处理和操作，才能以一组特征的形式在矩形数据中表示（参见第2页的“结构化数据的元素”）。关系数据库中的数据必须被提取并放入单个表中，以进行大多数数据分析和建模任务。

矩形数据的关键术语

  • 数据框（Data frame） 矩形数据（如电子表格）是统计和机器学习模型的基本数据结构。
  • 特征（Feature） 表中的一列通常被称为特征。 同义词：attribute（属性）、input（输入）、predictor（预测变量）、variable（变量）
  • 结果（Outcome） 许多数据科学项目涉及预测一个结果——通常是是/否的结果（在表1-1中，它是“拍卖是否具有竞争力”）。在实验或研究中，特征有时被用来预测结果。 同义词：dependent variable（因变量）、response（响应）、target（目标）、output（输出）
  • 记录（Records） 表中的一行通常被称为记录。 同义词：case（案例）、example（例子）、instance（实例）、observation（观察）、pattern（模式）、sample（样本）

T1.1

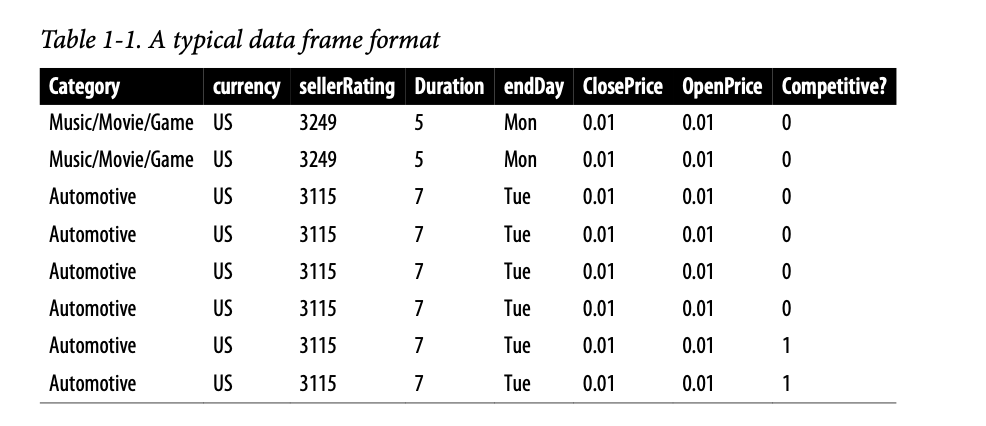
在表1-1中，混合了测量或计数的数据（例如持续时间和价格）和类别数据（例如类别和货币）。如前所述，类别变量的一种特殊形式是二元（是/否或0/1）变量，如表1-1最右边的列所示——一个指示变量，显示拍卖是否具有竞争力（有多个竞标者）。当场景是预测拍卖是否具有竞争力时，这个指示变量也恰好是一个结果变量。

数据框和索引

Data Frames and Indexes

传统数据库表有一个或多个列被指定为索引，本质上是一个行号。这可以极大地提高某些数据库查询的效率。在 Python 中，使用 pandas 库，基本的矩形数据结构是 DataFrame 对象。默认情况下，DataFrame 会根据行的顺序创建一个自动整数索引。在 pandas 中，也可以设置多级/分层索引以提高某些操作的效率。

在 R 中，基本的矩形数据结构是 data.frame 对象。data.frame 也有一个基于行顺序的隐式整数索引。原生的 R data.frame 不支持用户指定的或多级索引，但可以通过 row.names 属性创建自定义键。为了克服这一不足，两个新的包正在被广泛使用：data.table 和 dplyr。两者都支持多级索引，并在处理 data.frame 时提供了显著的速度提升。

警告：

术语差异 Terminology Differences

矩形数据的术语可能令人困惑。统计学家和数据科学家对同一事物使用不同的术语。对于统计学家来说，predictor variables（预测变量）用于模型中以预测 response 或 dependent variable（响应或因变量）。对于数据科学家来说，features（特征）用于预测 target（目标）。有一个同义词尤其令人困惑：计算机科学家将 sample（样本）这个术语用于单行；而对于统计学家来说，sample 意味着多行的集合。

非矩形数据结构

Nonrectangular Data Structures

除了矩形数据之外，还有其他数据结构。

时间序列数据记录同一变量的连续测量值。它是统计预测方法的原始材料，也是由设备（物联网）产生的数据的关键组成部分。

空间数据结构用于地图和位置分析，比矩形数据结构更复杂、种类更多。在对象表示中，数据的焦点是一个对象（例如，一栋房子）及其空间坐标。相比之下，字段视图则侧重于小的空间单元和相关度量的值（例如，像素亮度）。

图（或网络）数据结构用于表示物理、社交和抽象关系。例如，像 Facebook 或 LinkedIn 这样的社交网络图可以表示网络中人与人之间的联系。由道路连接的分销枢纽是物理网络的一个例子。图结构对于某些类型的问题很有用，例如网络优化和推荐系统。

每种数据类型在数据科学中都有其专门的方法。本书的重点是矩形数据，它是预测建模的基本构建块。

警告：

统计学中的“图” Graphs in Statistics在计算机科学和信息技术中，“图（graph）”这个术语通常指实体之间连接的描绘，以及底层的数据结构。而在统计学中，“图”则用于指各种图表和可视化，不仅仅是实体之间的连接，并且该术语仅适用于可视化，而不适用于数据结构。

关键思想

  • 数据科学中的基本数据结构是一个矩形矩阵，其中行是记录，列是变量（特征）。
  • 术语可能令人困惑；由于对数据科学做出贡献的不同学科（统计学、计算机科学和信息技术），存在各种同义词。

位置估计

Estimates of Location

测量或计数的数据变量可能具有数千个不同的值。探索数据的一个基本步骤是获取每个特征（变量）的“典型值”：对大多数数据所在位置的估计（即其中心趋势）。

位置估计的关键术语

  • 均值（Mean） 所有值的总和除以值的数量。 同义词：average（平均值）
  • 加权平均值（Weighted mean） 所有值乘以一个权重，再除以所有权重的总和。 同义词：weighted average（加权平均值）
  • 中位数（Median） 数据中有一半值在其之上，一半值在其之下的那个值。 同义词：50th percentile（第50百分位数）
  • 百分位数（Percentile） 数据中有 \(P\) 百分比的值在其之下的那个值。 同义词：quantile（分位数）
  • 加权中位数（Weighted median） 排序数据中，权重的总和有一半在其之上，一半在其之下的那个值。
  • 截尾均值（Trimmed mean） 在去除固定数量的极端值后，所有值的平均值。 同义词：truncated mean（截断均值）
  • 稳健（Robust） 对极端值不敏感。 同义词：resistant（有抵抗力）
  • 异常值（Outlier） 与大部分数据非常不同的数据值。 同义词：extreme value（极端值）

乍一看，汇总数据似乎相当简单：只需计算数据的均值。然而，尽管均值易于计算且方便使用，但它可能并非总是衡量中心值的最佳方法。因此，统计学家开发并推广了几个替代均值的估计量。

通用注解：度量与估计 Metrics and Estimates 统计学家经常使用“估计（estimate）”一词来指代从现有数据中计算出的值，以区分我们从数据中看到的内容与理论上的真实或精确状态。数据科学家和业务分析师更倾向于将此类值称为“度量（metric）”。这种差异反映了统计学与数据科学各自的方法：考虑不确定性是统计学学科的核心，而具体的业务或组织目标是数据科学的焦点。因此，统计学家进行估计，而数据科学家进行度量。

均值

Mean

最基本的位置估计量是均值（mean），或称平均值。均值是所有值的总和除以值的数量。考虑以下这组数字：\(\{3, 5, 1, 2\}\)。均值为 \((3 + 5 + 1 + 2) / 4 = 11 / 4 = 2.75\)。您会看到符号 \(\bar{x}\)（读作“x-bar”）用于表示从总体中抽取的样本的均值。计算一组 \(n\) 个值 \(x_1, x_2, \dots, x_n\) 的均值的公式是：

\[ \text{Mean} = \bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} \]

通用注解：

\(N(或 n)\)指代记录或观察的总数。在统计学中，如果指的是总体，则大写；如果指的是从总体中抽取的样本，则小写。在数据科学中，这种区别并不重要，因此您可能会看到这两种用法。

均值的一个变体是截尾均值（trimmed mean），其计算方法是先剔除排序后两端固定数量的值，然后对剩余的值求平均。用 \(x_{(1)}, x_{(2)}, \dots, x_{(n)}\) 表示排序后的值，其中 \(x_{(1)}\) 是最小值，\(x_{(n)}\) 是最大值，计算剔除 \(p\) 个最小和最大值的截尾均值的公式是：

\[ \text{Trimmed mean} = \bar{x}_{t} = \frac{\sum_{i=p+1}^{n-p} x_{(i)}}{n-2p} \]

截尾均值消除了极端值的影响。例如，在国际跳水比赛中，会去掉五名裁判的最高分和最低分，最终得分是剩余三名裁判的平均分。这使得单个裁判难以操纵分数，可能为了偏袒他们本国的选手。截尾均值被广泛使用，在许多情况下优于使用普通均值——有关进一步讨论，请参见第10页的“中位数和稳健估计”。

另一种类型的均值是加权平均值（weighted mean），其计算方法是将每个数据值 \(x_i\) 乘以用户指定的权重 \(w_i\)，然后将它们的总和除以权重的总和。加权平均值的公式是：

\[ \text{Weighted mean} = \bar{x}_w = \frac{\sum_{i=1}^{n} w_i x_i}{\sum_{i=1}^{n} w_i} \]

使用加权平均值有两个主要动机：

  • 一些值的内在变异性比其他值更大，变异性大的观测值被赋予较低的权重。例如，如果我们从多个传感器取平均值，其中一个传感器的精度较低，那么我们可能会降低该传感器数据的权重。
  • 收集到的数据不能平等地代表我们感兴趣的不同群体。例如，由于在线实验的进行方式，我们可能没有一组数据能够准确反映用户群中的所有群体。为了纠正这一点，我们可以给那些代表性不足的群体的值赋予更高的权重。

中位数和稳健估计

Median and Robust Estimates

中位数是排序数据列表中的中间数。如果数据值的数量是偶数，中间值并不是数据集中实际存在的某个值，而是将排序数据分为上半部分和下半部分的两个值的平均值。与使用所有观察值的均值相比，中位数仅依赖于排序数据中心的值。虽然这看似是一个缺点，因为均值对数据更为敏感，但在许多情况下，中位数是衡量位置的更好指标。比如说，我们想看看西雅图华盛顿湖周围社区的典型家庭收入。在比较 Medina 社区和 Windermere 社区时，如果使用均值会产生非常不同的结果，因为比尔·盖茨住在 Medina。如果我们使用中位数，比尔·盖茨有多富有都无关紧要——中间观察值的位置将保持不变。

出于使用加权均值的原因，也可以计算加权中位数。与中位数一样，我们首先对数据进行排序，尽管每个数据值都有一个相关的权重。加权中位数不是中间的数字，而是一个值，使得排序列表中较低和较高部分权重的总和相等。像中位数一样，加权中位数对异常值是稳健的。

异常值

Outliers

中位数被称为位置的稳健估计，因为它不受可能使结果扭曲的异常值（极端情况）的影响。异常值是数据集中与大多数其他值非常不同的任何值。异常值的确切定义有些主观，尽管在各种数据摘要和图表中使用了某些惯例（参见第20页的“百分位数和箱线图”）。作为异常值本身并不意味着数据值无效或有误（如比尔·盖茨的例子）。尽管如此，异常值通常是由于数据错误造成的，例如混合了不同单位的数据（千米与米）或传感器读数不良。当异常值是糟糕数据的结果时，均值将导致一个糟糕的位置估计，而中位数仍然是有效的。无论如何，异常值都应该被识别出来，并且通常值得进一步调查。

通用注解：异常检测Anomaly Detection

与典型的数据分析不同，在典型数据分析中，异常值有时具有信息性，有时是麻烦，而在异常检测中，感兴趣的点就是异常值，而大部分数据主要用于定义“正常”，以此来衡量异常。

中位数不是唯一的位置稳健估计。事实上，截尾均值被广泛用于避免异常值的影响。例如，截去数据底部和顶部的10%（一个常见的选择）将为除了最小的数据集之外的所有数据集提供对抗异常值的保护。截尾均值可以被认为是中位数和均值之间的一种折衷：它对数据中的极端值是稳健的，但使用更多的数据来计算位置估计。

知识点：

其他位置的稳健度量 Other Robust Metrics for Location

统计学家已经开发了大量其他用于位置的估计量，其主要目标是开发比均值更稳健、也更有效（即，更能辨别数据集之间微小位置差异）的估计量。虽然这些方法对于小型数据集可能有用，但对于大型或甚至中等大小的数据集，它们不太可能提供额外的好处。

示例

人口和谋杀率的位置估计

Example: Location Estimates of Population and Murder Rates

T1.2

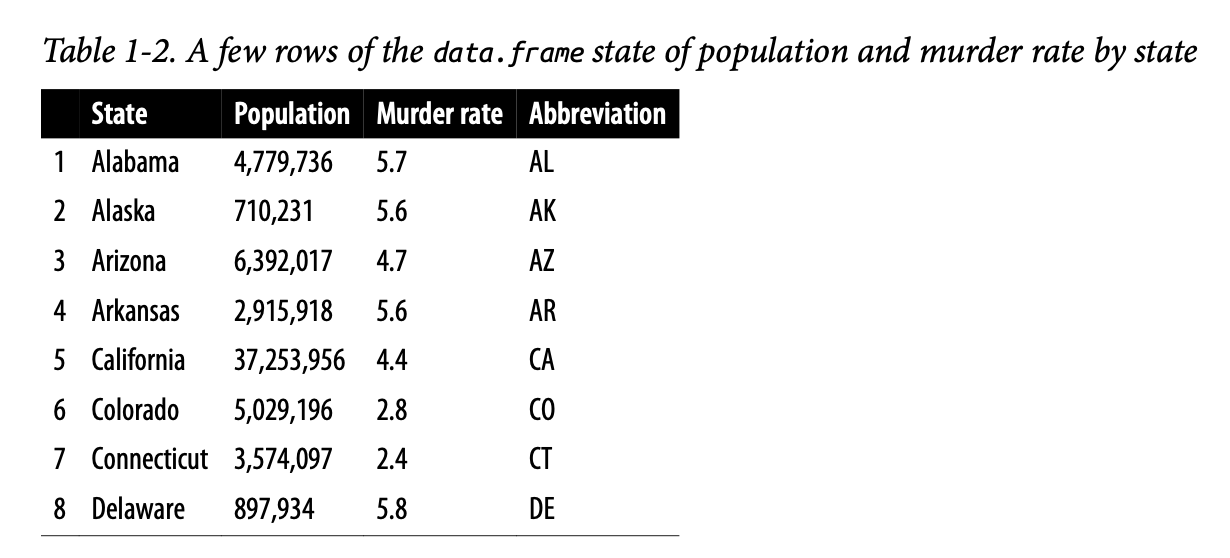
表1-2显示了数据集中前几行，其中包含美国各州的人口和谋杀率（单位为每年每10万人中的谋杀案数）（2010年人口普查）。

使用 R 计算人口的均值、截尾均值和中位数：

1
2
3
4
5
6
7
> state <- read.csv('state.csv')
> mean(state[['Population']])
[1] 6162876
> mean(state[['Population']], trim=0.1)
[1] 4783697
> median(state[['Population']])
[1] 4436370

要在 Python 中计算均值和中位数，我们可以使用数据框的 pandas 方法。截尾均值需要 scipy.stats 中的 trim_mean 函数：

1
2
3
4
state = pd.read_csv('state.csv')
state['Population'].mean()
trim_mean(state['Population'], 0.1)
state['Population'].median()

均值大于截尾均值，截尾均值大于中位数。这是因为截尾均值排除了最大和最小的五个州（trim=0.1 从每一端剔除10%）。如果我们想计算全国的平均谋杀率，我们需要使用加权均值或中位数来考虑各州的不同人口。由于基础 R 没有加权中位数的函数，我们需要安装一个像 matrixStats 这样的包：

1
2
3
4
5
> weighted.mean(state[['Murder.Rate']], w=state[['Population']])
[1] 4.445834
> library('matrixStats')
> weightedMedian(state[['Murder.Rate']], w=state[['Population']])
[1] 4.4

加权均值可以通过 NumPy 获得。对于加权中位数，我们可以使用专门的包 wquantiles：

1
2
np.average(state['Murder.Rate'], weights=state['Population'])
wquantiles.median(state['Murder.Rate'], weights=state['Population'])

在这种情况下，加权均值和加权中位数大致相同。

关键思想

  • 位置的基本度量是均值，但它可能对极端值（异常值）敏感。
  • 其他度量（中位数、截尾均值）对异常值和不寻常的分布不太敏感，因此更具稳健性。

变异性估计

Estimates of Variability

位置只是概括一个特征的一个维度。第二个维度，变异性（也称为离散度），衡量数据值是紧密聚集还是分散开来。统计学的核心在于变异性：测量它、减少它、区分随机变异与真实变异、识别真实变异的各种来源，并在变异存在的情况下做出决策。

变异性度量的关键术语

  • 偏差（Deviations） 观察值与位置估计值之间的差。 同义词：errors（误差）、residuals（残差）
  • 方差（Variance） 观察值与均值之间偏差的平方和，除以 \(n-1\)，其中 \(n\) 是数据值的数量。 同义词：mean-squared-error（均方误差）
  • 标准差（Standard deviation） 方差的平方根。
  • 平均绝对偏差（Mean absolute deviation） 观察值与均值之间偏差的绝对值的均值。 同义词：l1-norm（L1范数）、Manhattan norm（曼哈顿范数）
  • 中位数绝对偏差（Median absolute deviation from the median） 观察值与中位数之间偏差的绝对值的中位数。
  • 极差（Range） 数据集中最大值和最小值之间的差。
  • 顺序统计量（Order statistics） 基于从最小到最大排序的数据值计算的度量。 同义词：ranks（秩）
  • 百分位数（Percentile） 数据中 \(P\) 百分比的值取这个值或更小，\((100-P)\) 百分比的值取这个值或更大的那个值。 同义词：quantile（分位数）
  • 四分位距（Interquartile range） 第75百分位数和第25百分位数之间的差。 同义词：IQR

正如衡量位置有不同的方法（均值、中位数等），衡量变异性也有不同的方法。

标准差和相关估计

Standard Deviation and Related Estimates

最广泛使用的变异性估计是基于位置估计与观测数据之间的差异或偏差。对于一组数据 \(\{1, 4, 4\}\)，均值为3，中位数为4。与均值的偏差是：\(1 - 3 = -2\)，\(4 - 3 = 1\)，\(4 - 3 = 1\)。这些偏差告诉我们数据围绕中心值的离散程度。

衡量变异性的一种方法是估计这些偏差的典型值。对偏差本身求平均值不会告诉我们太多——负偏差会抵消正偏差。事实上，与均值的偏差总和正好为零。相反，一个简单的方法是取与均值偏差的绝对值的平均值。在前面的例子中，偏差的绝对值是 \(\{2, 1, 1\}\)，它们的平均值是 \((2 + 1 + 1) / 3 = 1.33\)。这被称为平均绝对偏差，其计算公式为：

\[ \text{平均绝对偏差} = \frac{\sum_{i=1}^{n} |x_i - \bar{x}|}{n} \]

其中 \(\bar{x}\) 是样本均值。

最著名的变异性估计是方差和标准差，它们基于平方偏差。方差是平方偏差的平均值，标准差是方差的平方根：

\[ \text{方差} = s^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1} \] \[ \text{标准差} = s = \sqrt{\text{方差}} \]

标准差比方差更容易解释，因为它与原始数据处于相同的尺度。然而，由于其更复杂、更不直观的公式，统计学中对标准差的偏爱胜过平均绝对偏差，这可能看起来很奇特。它之所以享有盛誉，归功于统计学理论：在数学上，使用平方值比使用绝对值方便得多，尤其是对于统计模型。

自由度，以及 \(n\) 还是 \(n-1\)？

在统计学书籍中，总会讨论为什么方差公式的分母是 \(n-1\) 而不是 \(n\)，这引出了自由度的概念。这种区别并不重要，因为 \(n\) 通常足够大，以至于除以 \(n\) 或 \(n-1\) 都没有太大区别。但如果您感兴趣，这里是原因。它基于一个前提：您想根据样本对总体进行估计。

如果您在方差公式中使用直观的分母 \(n\)，您将低估总体中方差和标准差的真实值。这被称为有偏估计（biased estimate）。然而，如果您用 \(n-1\) 而不是 \(n\) 来除，方差就变成了无偏估计（unbiased estimate）。

要完全解释为什么使用 \(n\) 会导致有偏估计，需要自由度的概念，它考虑了计算估计量时的约束数量。在这种情况下，有 \(n-1\) 个自由度，因为存在一个约束：标准差的计算依赖于样本均值。对于大多数问题，数据科学家不需要担心自由度。

无论是方差、标准差还是平均绝对偏差，它们都不稳健，对异常值和极端值敏感（有关位置的稳健估计的讨论，请参见第10页的“中位数和稳健估计”）。方差和标准差由于基于平方偏差，对异常值尤其敏感。

变异性的一个稳健估计是中位数绝对偏差（MAD）：

\[ \text{中位数绝对偏差} = \text{Median}\{|x_1 - m|, |x_2 - m|, \dots, |x_N - m|\} \]

其中 \(m\) 是中位数。像中位数一样，MAD不受极端值的影响。也可以计算类似于截尾均值的截尾标准差（参见第9页的“均值”）。

通用注解：

方差、标准差、平均绝对偏差和中位数绝对偏差即使在数据来自正态分布的情况下，也不是等价的估计量。事实上，标准差总是大于平均绝对偏差，而平均绝对偏差本身又大于中位数绝对偏差。有时，中位数绝对偏差会乘以一个常数比例因子，以便在正态分布的情况下，将 MAD 放在与标准差相同的尺度上。常用的因子是1.4826，这意味着50%的正态分布落在 ±MAD 的范围内（例如，参见 https://oreil.ly/SfDk2）。

基于百分位数的估计

Estimates Based on Percentiles

另一种估计离散度的方法是查看排序数据的扩展（spread）。基于排序（排名）数据的统计量被称为顺序统计量（order statistics）。最基本的度量是极差（range）：最大值和最小值之间的差。最小值和最大值本身很有用，有助于识别异常值，但极差对异常值极其敏感，作为数据离散度的通用度量用处不大。

为了避免对异常值的敏感性，我们可以查看剔除两端值后数据的极差。形式上，这些类型的估计基于百分位数之间的差。在一个数据集中，第 \(P\) 个百分位数是一个值，至少有 \(P\) 百分比的值取该值或更小，并且至少有 \((100-P)\) 百分比的值取该值或更大。例如，要找到第80个百分位数，请对数据进行排序。然后，从最小值开始，前进到距离最大值80%的位置。请注意，中位数与第50个百分位数是同一回事。百分位数本质上与分位数（quantile）相同，分位数用小数索引（因此 .8 分位数与第80百分位数相同）。

一个常见的变异性度量是第25百分位数和第75百分位数之间的差，称为四分位距（interquartile range，IQR）。这里有一个简单的例子：\(\{3,1,5,3,6,7,2,9\}\)。我们对其进行排序得到 \(\{1,2,3,3,5,6,7,9\}\)。第25百分位数在2.5处，第75百分位数在6.5处，因此四分位距为 \(6.5 - 2.5 = 4\)。软件可能有略微不同的方法，会产生不同的答案（参见下面的提示）；通常，这些差异很小。

对于非常大的数据集，计算精确的百分位数在计算上可能非常昂贵，因为它需要对所有数据值进行排序。机器学习和统计软件使用特殊算法，例如 [Zhang-Wang-2007]，来获得可以非常快速计算并保证具有一定准确度的近似百分位数。

知识点：

百分位数：精确定义 Percentile: Precise Definition

如果我们的数据数量是偶数（\(n\) 是偶数），那么根据前面的定义，百分位数是模糊的。事实上，在满足以下条件的 \(j\) 的情况下，我们可以取任何介于顺序统计量 \(x_{(j)}\) 和 \(x_{(j+1)}\) 之间的值： \[ \frac{100 \cdot j}{n} \le P < \frac{100 \cdot (j+1)}{n} \]

正式地，百分位数是加权平均值：

\[ \text{百分位数 } P = (1 - w)x_{(j)} + wx_{(j+1)} \]

其中 \(w\) 是介于0和1之间的一些权重。统计软件在选择 \(w\) 的方法上略有不同。事实上，R 函数 quantile 提供了九种不同的计算分位数的方法。除了小型数据集，您通常不需要担心百分位数的确切计算方式。在撰写本文时，Python 的 numpy.quantile 仅支持一种方法，即线性插值。

示例

州人口的变异性估计

Example: Variability Estimates of State Population

T1.3

表1-3（为方便起见重复了表1-2）显示了数据集中包含每个州的人口和谋杀率的前几行。

使用 R 的内置函数来计算标准差（sd）、四分位距（IQR）和中位数绝对偏差（mad），我们可以计算州人口数据的变异性估计：

1
2
3
4
5
6
> sd(state[['Population']])
[1] 6848235
> IQR(state[['Population']])
[1] 4847308
> mad(state[['Population']])
[1] 3849870

pandas 数据框提供了计算标准差和分位数的方法。使用分位数，我们可以轻松确定 IQR。对于稳健的 MAD，我们使用 statsmodels 包中的 robust.scale.mad 函数：

1
2
3
state['Population'].std()
state['Population'].quantile(0.75) - state['Population'].quantile(0.25)
robust.scale.mad(state['Population'])

标准差几乎是 MAD 的两倍（在 R 中，默认情况下，MAD 的尺度被调整为与均值在同一尺度上）。这并不奇怪，因为标准差对异常值很敏感。

关键思想

  • 方差和标准差是最广泛使用和常规报告的变异性统计量。
  • 两者都对异常值敏感。
  • 更稳健的度量包括平均绝对偏差、中位数绝对偏差和百分位数（分位数）。

探索数据分布

Exploring the Data Distribution

我们所涵盖的每一个估计量都将数据汇总为一个单一数字，来描述数据的位置或变异性。探索数据的整体分布也很有用。

探索分布的关键术语

  • 箱线图（Boxplot） Tukey 提出的一种图，作为快速可视化数据分布的方法。 同义词：box and whiskers plot（盒须图）
  • 频率表（Frequency table） 落入一组区间（箱）的数值数据的计数。
  • 直方图（Histogram） 频率表的图，其中箱在 x 轴上，计数（或比例）在 y 轴上。虽然在视觉上相似，但条形图不应与直方图混淆。有关差异的讨论，请参见第27页的“探索二元和类别数据”。
  • 密度图（Density plot） 直方图的平滑版本，通常基于核密度估计。

百分位数和箱线图

Percentiles and Boxplots

在第16页的“基于百分位数的估计”中，我们探讨了百分位数如何用于衡量数据的离散度。百分位数对于汇总整个分布也很有价值。通常会报告四分位数（第25、50和75百分位数）和十分位数（第10、20、...、90百分位数）。百分位数对于汇总分布的尾部（外部范围）特别有价值。流行文化创造了“百分之一的人”（one-percenters）这个术语来指代那些财富处于第99百分位数的人。

T1.4

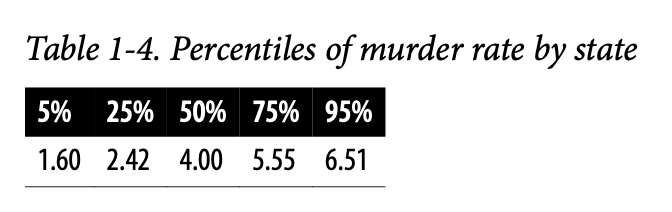
表1-4显示了按州划分的谋杀率的一些百分位数。在 R 中，这将由 quantile 函数生成：

1
quantile(state[['Murder.Rate']], p=c(.05, .25, .5, .75, .95))
1
2
   5%   25%   50%   75%   95% 
1.600 2.425 4.000 5.550 6.510

pandas 数据框方法 quantile 在 Python 中提供此功能：

1
state['Murder.Rate'].quantile([0.05, 0.25, 0.5, 0.75, 0.95])

中位数是每10万人中有4起谋杀案，尽管存在相当大的变异性：第5百分位数仅为1.6，而第95百分位数是6.51。

F1.2

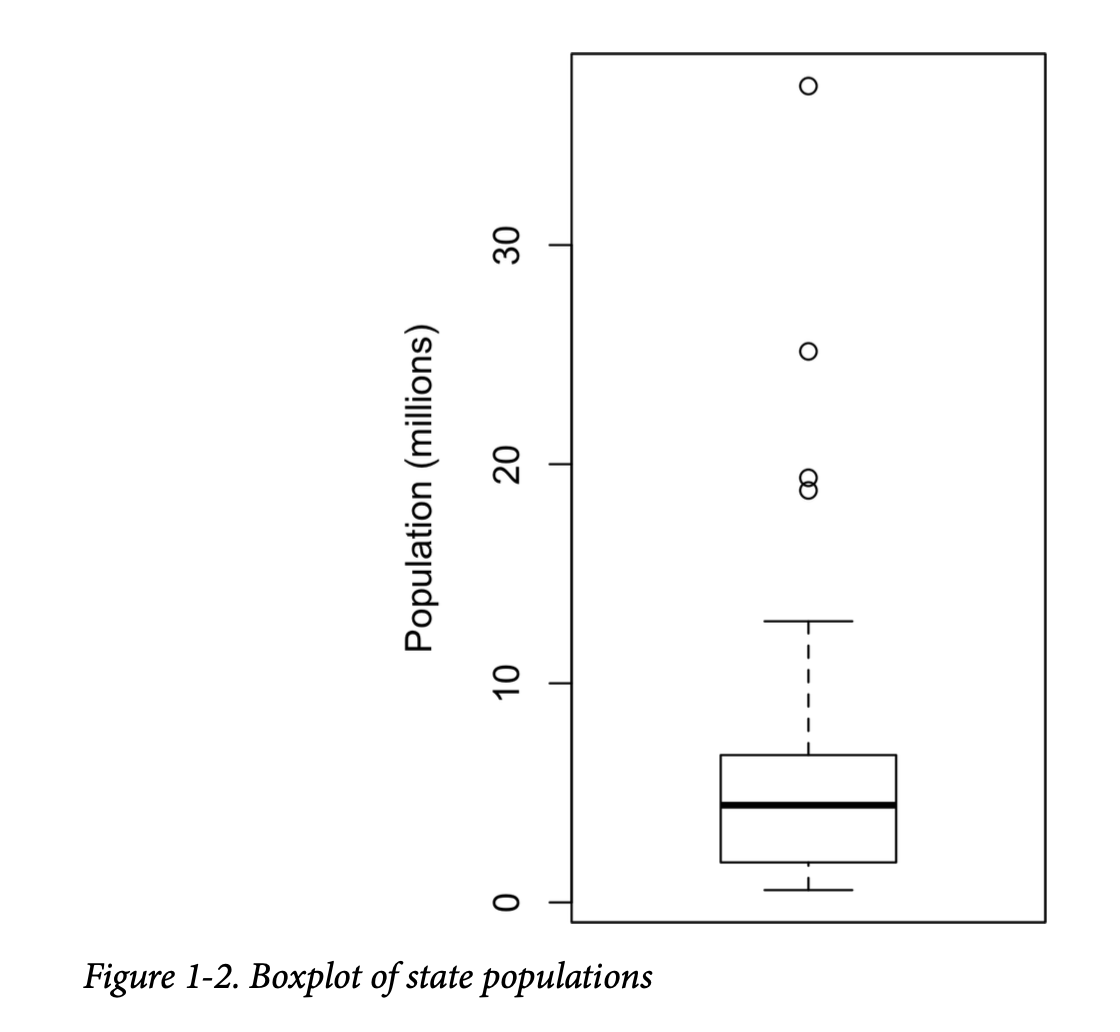
由 Tukey [Tukey-1977] 引入的箱线图基于百分位数，提供了一种快速可视化数据分布的方法。图1-2显示了由 R 生成的按州划分的人口箱线图：

1
boxplot(state[['Population']]/1000000, ylab='Population (millions)')

pandas 为数据框提供了许多基本的探索性绘图；其中之一就是箱线图：

1
2
ax = (state['Population']/1_000_000).plot.box()
ax.set_ylabel('Population (millions)')

从这个箱线图我们可以立即看到，州人口中位数约为500万，一半的州人口介于约200万到约700万之间，并且存在一些人口异常值。箱子的顶部和底部分别是第75和第25百分位数。中位数由箱子中的水平线显示。虚线，被称为须（whiskers），从箱子的顶部和底部延伸，表示大部分数据的范围。箱线图有许多变体；例如，参见 R 函数 boxplot 的文档 [R-base-2015]。默认情况下，R 函数将须延伸到箱子以外的最远点，但不会超过 1.5倍的 IQR。Matplotlib 使用相同的实现；其他软件可能使用不同的规则。

须线之外的任何数据都作为单个点或圆圈绘制（通常被认为是异常值）。

频率表和直方图

Frequency Tables and Histograms

T1.5

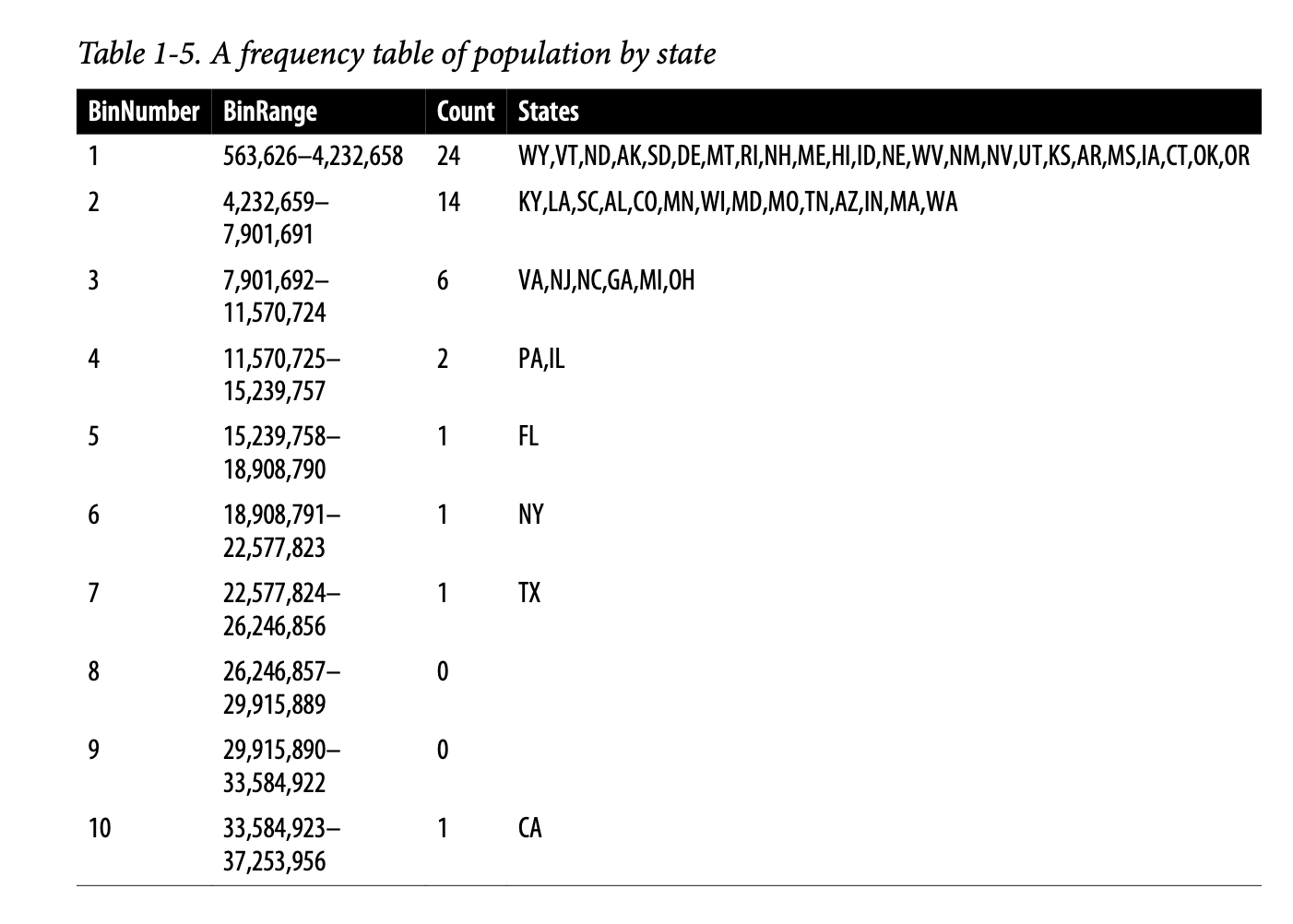
变量的频率表将变量范围划分为等距的片段，并告诉我们有多少个值落入每个片段中。表1-5显示了在 R 中计算的按州划分的人口频率表：

1
2
3
4
5
breaks <- seq(from=min(state[['Population']]),
to=max(state[['Population']]), length=11)
pop_freq <- cut(state[['Population']], breaks=breaks,
right=TRUE, include.lowest=TRUE)
table(pop_freq)
1
2
3
4
5
6
7
8
(563626,4232659] (4232659,7901692] (7901692,11570725] 
               24                13                 6 
(11570725,15239758] (15239758,18908791] (18908791,22577824] 
                 2                  1                  2 
(22577824,26246857] (26246857,29915890] (29915890,33584923] 
                 1                  1                  0 
(33584923,37253956] 
                 1

pandas.cut 函数创建一个系列，将值映射到这些片段。使用 value_counts 方法，我们得到频率表：

1
2
binnedPopulation = pd.cut(state['Population'], 10)
binnedPopulation.value_counts()
1
2
3
4
5
6
7
8
9
10
11
(526935.67, 4232659.0]     24
(4232659.0, 7901692.0]     13
(7901692.0, 11570725.0]     6
(15239758.0, 18908791.0]     2
(18908791.0, 22577824.0]     2
(11570725.0, 15239758.0]     1
(33584923.0, 37253956.0]     1
(22577824.0, 26246857.0]     1
(26246857.0, 29915890.0]     1
(29915890.0, 33584923.0]     0
Name: Population, dtype: int64

人口最少的州是怀俄明州，有563,626人，人口最多的州是加利福尼亚州，有37,253,956人。这给了我们一个 \(37,253,956 - 563,626 = 36,690,330\) 的范围，我们必须将其划分为大小相等的箱——假设有10个箱。对于10个大小相等的箱，每个箱的宽度将是 \(3,669,033\)，因此第一个箱的范围将是从563,626到4,232,658。相比之下，最顶部的箱，从33,584,923到37,253,956，只有一个州：加利福尼亚。加利福尼亚下面的两个箱是空的，直到我们到达德克萨斯州。重要的是要包括空箱；这些箱中没有值的事实是有用的信息。用不同大小的箱进行实验也很有用。如果箱太大，分布的重要特征可能会被掩盖。如果箱太小，结果会过于精细，从而失去看到大局的能力。

通用注解：

频率表和百分位数都通过创建箱来概括数据。一般来说，四分位数和十分位数的每个箱中将有相同的计数（等计数箱），但箱的大小会不同。相反，频率表的箱中将有不同的计数（等大小箱），而箱的大小将相同。

直方图是一种可视化频率表的方法，其中箱在 x 轴上，数据计数在 y 轴上。例如，在图1-3中，以1000万（1e+07）为中心的箱的范围大约是从800万到1200万，并且该箱中有六个州。

为了在 R 中创建与表1-5对应的直方图，使用 hist 函数并带 breaks 参数：

1
hist(state[['Population']], breaks=breaks)

pandas 使用 DataFrame.plot.hist 方法支持数据框的直方图。使用关键字参数 bins 来定义箱的数量。各种绘图方法返回一个 axis 对象，可以使用 Matplotlib 对可视化进行进一步的微调：

1
2
ax = (state['Population'] / 1_000_000).plot.hist(figsize=(4, 4))
ax.set_xlabel('Population (millions)')

F1.3

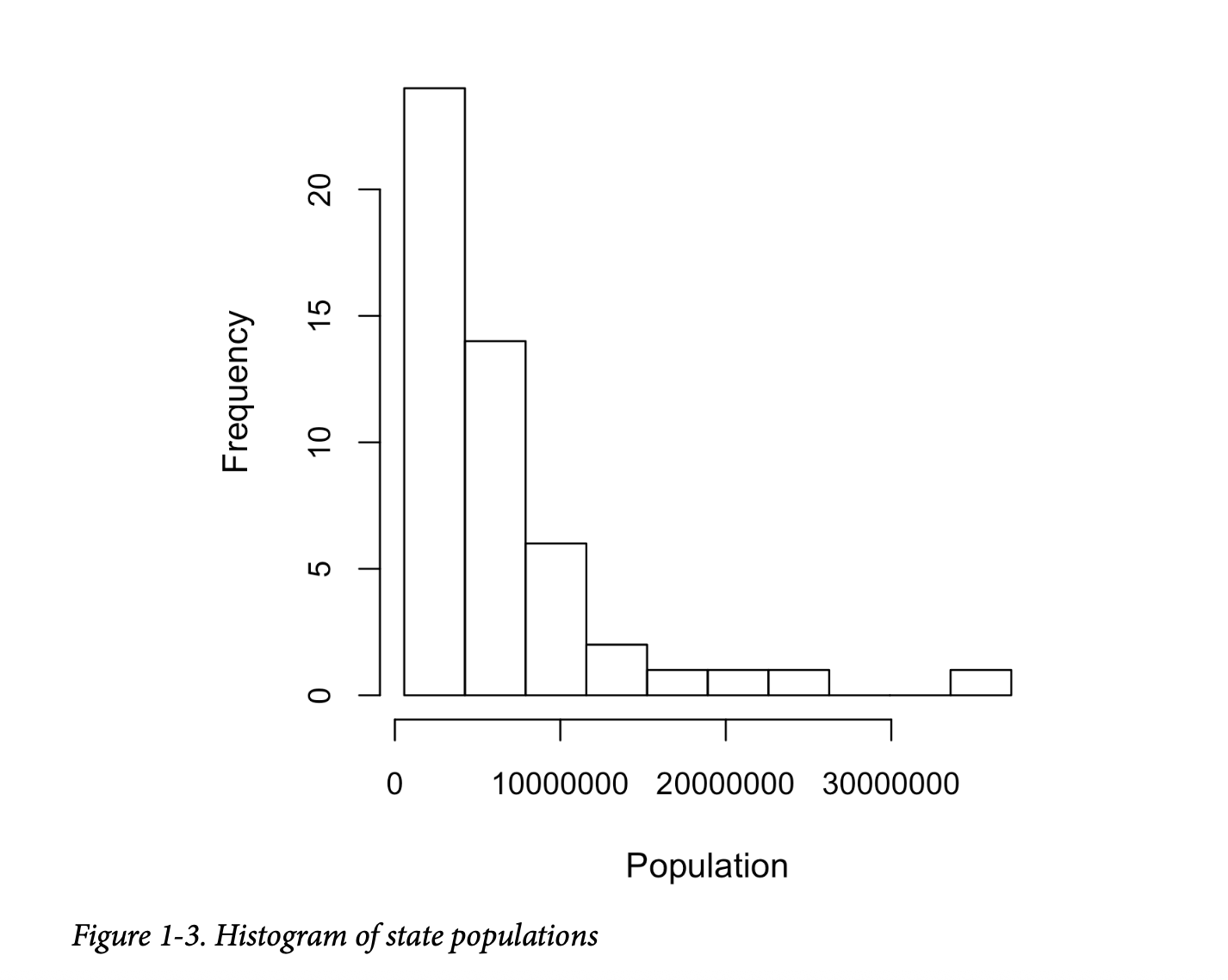
直方图如图1-3所示。通常，直方图的绘制方式使得：

  • 图中包含空箱。
  • 箱子的宽度相等。
  • 箱子的数量（或者等价地，箱子的大小）由用户决定。
  • 条形是连续的——条形之间没有空隙，除非有空箱。

知识点：

统计矩 Statistical Moments在统计理论中，位置和变异性分别被称为分布的第一和第二矩。第三和第四矩分别被称为偏度（skewness）和峰度（kurtosis）。偏度指的是数据是否偏向于更大或更小的值，而峰度则表示数据具有极端值的倾向。通常，不使用度量来测量偏度和峰度；相反，这些是通过视觉显示来发现的，例如图1-2和图1-3。

密度图和密度估计

Density Plots and Estimates

F1.4

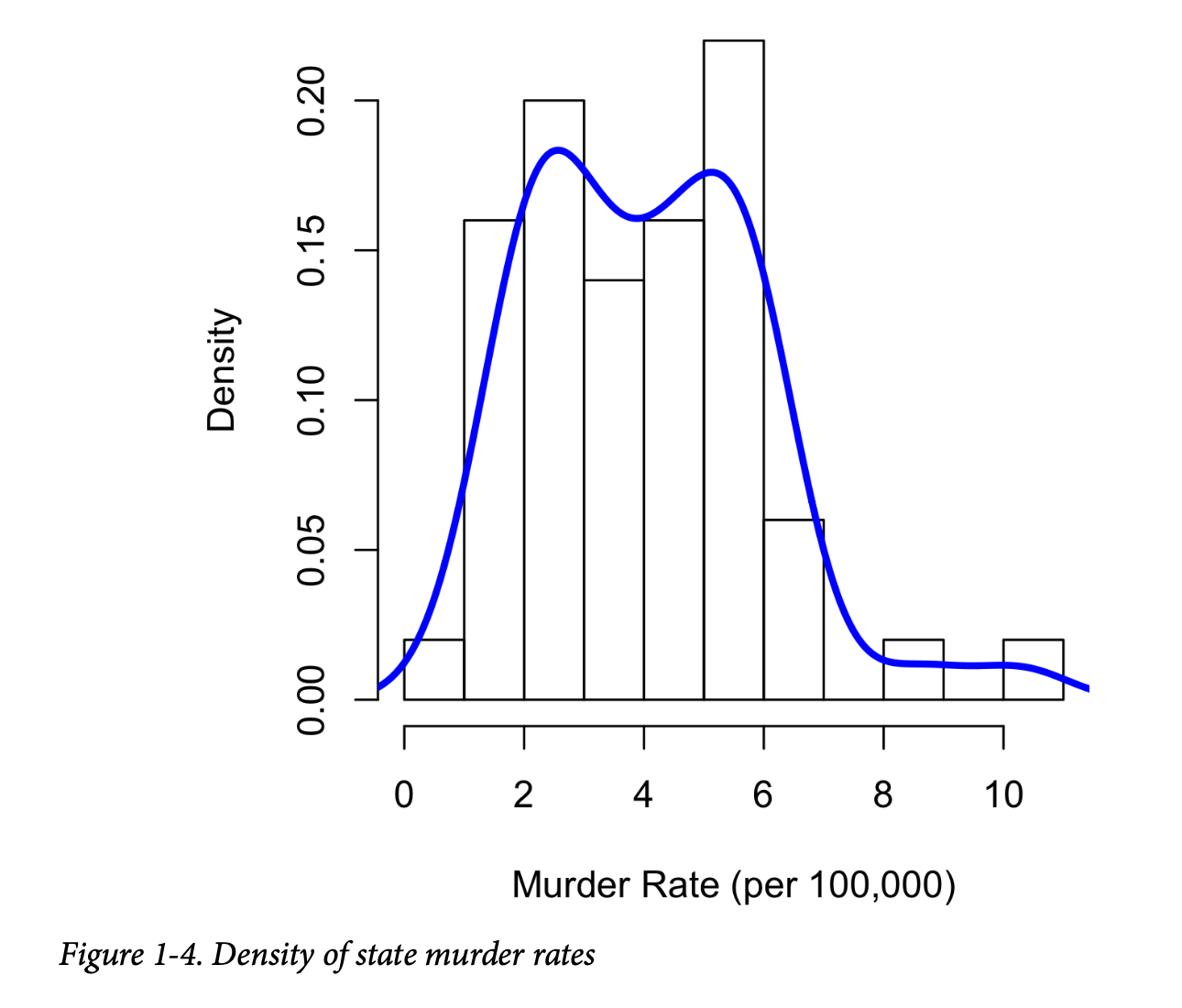
与直方图相关的是密度图，它以连续线的形式显示数据值的分布。密度图可以被认为是平滑的直方图，尽管它通常通过核密度估计直接从数据计算得到（有关简短教程，请参见 [Duong-2001]）。图1-4展示了一个叠加在直方图上的密度估计。在 R 中，您可以使用 density 函数计算密度估计：

1
2
hist(state[['Murder.Rate']], freq=FALSE)
lines(density(state[['Murder.Rate']]), lwd=3, col='blue')

pandas 提供了 density 方法来创建密度图。使用参数 bw_method 来控制密度曲线的平滑度：

1
2
3
ax = state['Murder.Rate'].plot.hist(density=True, xlim=[0,12], bins=range(1,12))
state['Murder.Rate'].plot.density(ax=ax)
ax.set_xlabel('Murder Rate (per 100,000)')

绘图函数通常接受一个可选的轴（ax）参数，这会使绘图被添加到同一张图上。

与图1-3中绘制的直方图的一个关键区别是y轴的刻度：密度图对应于将直方图绘制为比例而不是计数（在 R 中，您可以使用参数 freq=FALSE 指定这一点）。请注意，密度曲线下的总面积=1，并且您计算的是曲线下任意两点之间的面积，而不是箱中的计数，这对应于分布中介于这两点之间的比例。

知识点：

密度估计 Density Estimation

密度估计是一个丰富的课题，在统计文献中有悠久的历史。事实上，已经有超过20个 R 包发布，提供了用于密度估计的函数。[Deng-Wickham-2011] 对 R 包进行了全面综述，特别推荐了 ASH 或 KernSmooth。pandas 和 scikit-learn 中的密度估计方法也提供了很好的实现。对于许多数据科学问题，**没有必要担心各种类型的密度估计；使用基本函数就足够了。

关键思想

  • 频率直方图在 y 轴上绘制频率计数，在 x 轴上绘制变量值；它让人一目了然地了解数据的分布。
  • 频率表是直方图中频率计数的表格版本。
  • 箱线图——箱子的顶部和底部分别是第75和第25百分位数——也让人对数据分布有一个快速的了解；它经常用于并排显示以比较分布。
  • 密度图是直方图的平滑版本；它需要一个函数来基于数据估计一个图（当然，可能有多种估计方法）。

探索二元和类别数据

Exploring Binary and Categorical Data

对于类别数据，简单的比例或百分比就能说明数据的情况。

探索类别数据的关键术语

  • 众数（Mode） 数据集中最常出现的类别或值。
  • 期望值（Expected value） 当类别可以与数值关联时，这表示基于类别发生概率的平均值。
  • 条形图（Bar charts） 将每个类别的频率或比例绘制成条形。
  • 饼图（Pie charts） 将每个类别的频率或比例绘制成饼状图中的扇形。

T1.6

获取一个二元变量或只有几个类别的类别变量的摘要是相当容易的：我们只需计算1的比例，或重要类别的比例。例如，表1-6显示了自2010年以来达拉斯/沃斯堡机场（Dallas/Fort Worth Airport）航班延误的百分比，按延误原因划分。延误被归类为由航空公司控制的因素、空中交通管制（ATC）系统延误、天气、安保或晚到的入港飞机。

F1.5

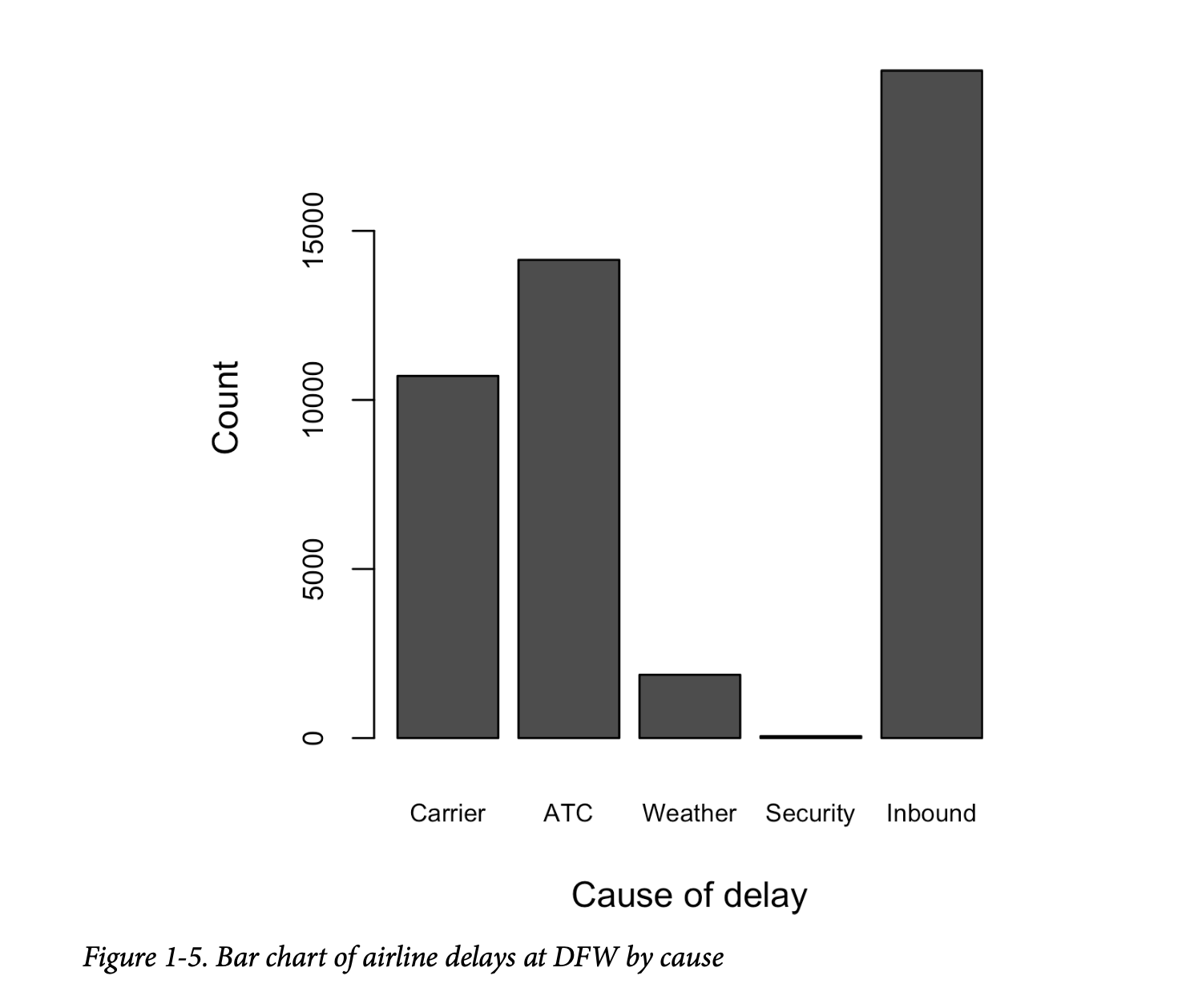
条形图在流行媒体中经常出现，是显示单个类别变量的常见可视化工具。类别列在x轴上，频率或比例列在y轴上。图1-5显示了达拉斯/沃斯堡（DFW）机场每年的延误情况，按原因划分，由R函数barplot生成：

1
2
barplot(as.matrix(dfw) / 6, cex.axis=0.8, cex.names=0.7,
xlab='Cause of delay', ylab='Count')

pandas也支持数据框的条形图：

1
2
3
ax = dfw.transpose().plot.bar(figsize=(4, 4), legend=False)
ax.set_xlabel('Cause of delay')
ax.set_ylabel('Count')

请注意，条形图与直方图相似；在条形图中，x轴表示因子变量的不同类别，而在直方图中，x轴表示单个变量在数值尺度上的值。在直方图中，条形通常彼此接触，间隙表示数据中未出现的值。在条形图中，条形彼此分离。

饼图是条形图的替代品，尽管统计学家和数据可视化专家通常避用饼图，因为它们在视觉上提供的信息较少（参见 [Few-2007]）。

通用注解：

将数值数据视为类别数据

在第22页的“频率表和直方图”中，我们研究了基于分箱数据的频率表。这隐式地将数值数据转换为有序因子。从这个意义上讲，直方图和条形图是相似的，只是条形图x轴上的类别没有顺序。将数值数据转换为类别数据是数据分析中一个重要且广泛使用的步骤，因为它降低了数据的复杂性（和大小）。这有助于在分析的初始阶段发现特征之间的关系。

众数

Mode

众数是数据中出现最频繁的值，如果出现平局则为多个值。例如，达拉斯/沃斯堡机场航班延误原因的众数是“入港”。另一个例子是，在美国大部分地区，宗教信仰的众数将是基督教。众数是类别数据的一种简单汇总统计量，通常不用于数值数据。

期望值

Expected Value

一种特殊类型的类别数据是其类别代表或可以映射到相同尺度上离散值的数据。例如，一家新云技术的营销人员提供两种服务级别，一种定价为每月300美元，另一种为每月50美元。营销人员提供免费网络研讨会以产生潜在客户，公司估计5%的参与者会注册300美元的服务，15%会注册50美元的服务，80%不会注册任何服务。出于财务目的，这些数据可以用一个单一的“期望值”来汇总，这是一种加权平均值的形式，其中权重是概率。

期望值的计算方法如下： 1. 将每个结果乘以其发生的概率。 2. 将这些值相加。

在云服务示例中，一个网络研讨会参与者的期望值是每月22.50美元，计算如下：

\[ EV = 0.05 \times 300 + 0.15 \times 50 + 0.80 \times 0 = 22.5 \] 期望值实际上是加权平均值的一种形式：它加入了未来预期和概率权重的概念，这些概率权重通常基于主观判断。期望值是商业估值和资本预算中的一个基本概念——例如，新收购公司五年利润的期望值，或者诊所新患者管理软件的预期成本节约。

概率

Probability

我们上面提到了一个值发生的概率。大多数人对概率有直观的理解，经常在天气预报（下雨的可能性）或体育分析（获胜的概率）中遇到这个概念。体育和比赛更多地以赔率来表达，赔率可以很容易地转换为概率（如果一支球队获胜的赔率是2比1，其获胜的概率是 \(2/(2+1) = 2/3\)）。然而，令人惊讶的是，当涉及到定义它时，概率的概念可能是深刻哲学讨论的来源。幸运的是，我们在这里不需要一个正式的数学或哲学定义。就我们的目的而言，一个事件发生的概率是如果情况可以重复无数次，它发生的次数所占的比例。这通常是一个想象中的构造，但它足以作为对概率的操作性理解。

关键思想

  • 类别数据通常用比例来汇总，并可以在条形图中可视化。
  • 类别可能代表不同的事物（苹果和橙子、男性和女性）、因子变量的级别（低、中、高），或已被分箱的数值数据。
  • 期望值是值乘以其发生概率的总和，常用于汇总因子变量的级别。

相关性

Correlation

在许多建模项目（无论是数据科学还是研究）中，探索性数据分析都涉及检查预测变量之间以及预测变量与目标变量之间的相关性。如果变量 X 和 Y（每个都有测量数据）的高值伴随着高值，低值伴随着低值，则称它们正相关。如果变量 X 的高值伴随着 Y 的低值，反之亦然，则变量负相关。

相关性的关键术语

  • 相关系数（Correlation coefficient） 衡量数值变量之间关联程度的度量（范围从 -1 到 +1）。
  • 相关矩阵（Correlation matrix） 一个表格，其中变量同时显示在行和列上，单元格中的值是变量之间的相关性。
  • 散点图（Scatterplot） 一个图，其中 x 轴是某个变量的值，y 轴是另一个变量的值。

考虑这两个变量，它们在从低到高的意义上是完全相关的：

1
2
v1: {1, 2, 3}
v2: {4, 5, 6}

它们的向量积之和是 \(1 \cdot 4 + 2 \cdot 5 + 3 \cdot 6 = 32\)。现在尝试打乱其中一个并重新计算——向量积之和永远不会高于32。所以这个积之和可以用作一个度量；也就是说，观察到的总和32可以与大量随机打乱的结果进行比较（事实上，这个想法与基于重采样（resampling-based）的估计有关；参见第97页的“置换检验”）。然而，这个度量产生的值本身并没有太大意义，除非参考重采样分布。

更有用的是一个标准化变体：相关系数（correlation coefficient），它提供了两个变量之间相关性的估计，并且始终在相同的尺度上。要计算皮尔逊相关系数（Pearson's correlation coefficient），我们将变量1与均值的偏差乘以变量2与均值的偏差，然后除以标准差的乘积：

\[ r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{(n-1)s_x s_y} \] 请注意，我们除以 \(n-1\) 而不是 \(n\)；有关更多详细信息，请参见第15页的“自由度，以及 n 还是 n-1？”。相关系数始终介于 +1（完全正相关）和 -1（完全负相关）之间；0表示没有相关性。

变量之间可能存在非线性关联，在这种情况下，相关系数可能不是一个有用的度量。税率和税收之间的关系就是一个例子：当税率从零增加时，税收也会增加。然而，一旦税率达到高水平并接近100%，逃税行为会增加，税收实际上会下降。

T1.7

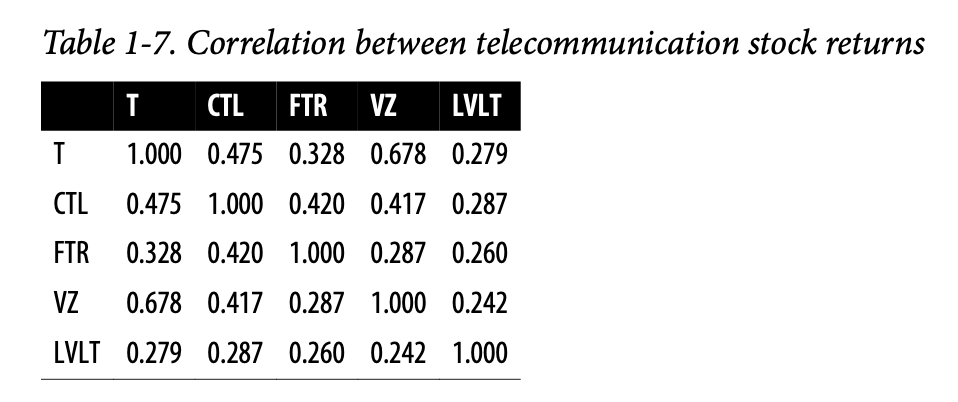
表1-7，被称为相关矩阵，显示了2012年7月至2015年6月期间电信股票日收益之间的相关性。从表中可以看出，威瑞森（VZ）和美国电话电报公司（T）的相关性最高。作为一家基础设施公司的 Level 3（LVLT），与其它公司的相关性最低。请注意对角线上的值都是1（一只股票与自身的相关性为1），以及对角线上方和下方的信息是冗余的。

F1.6

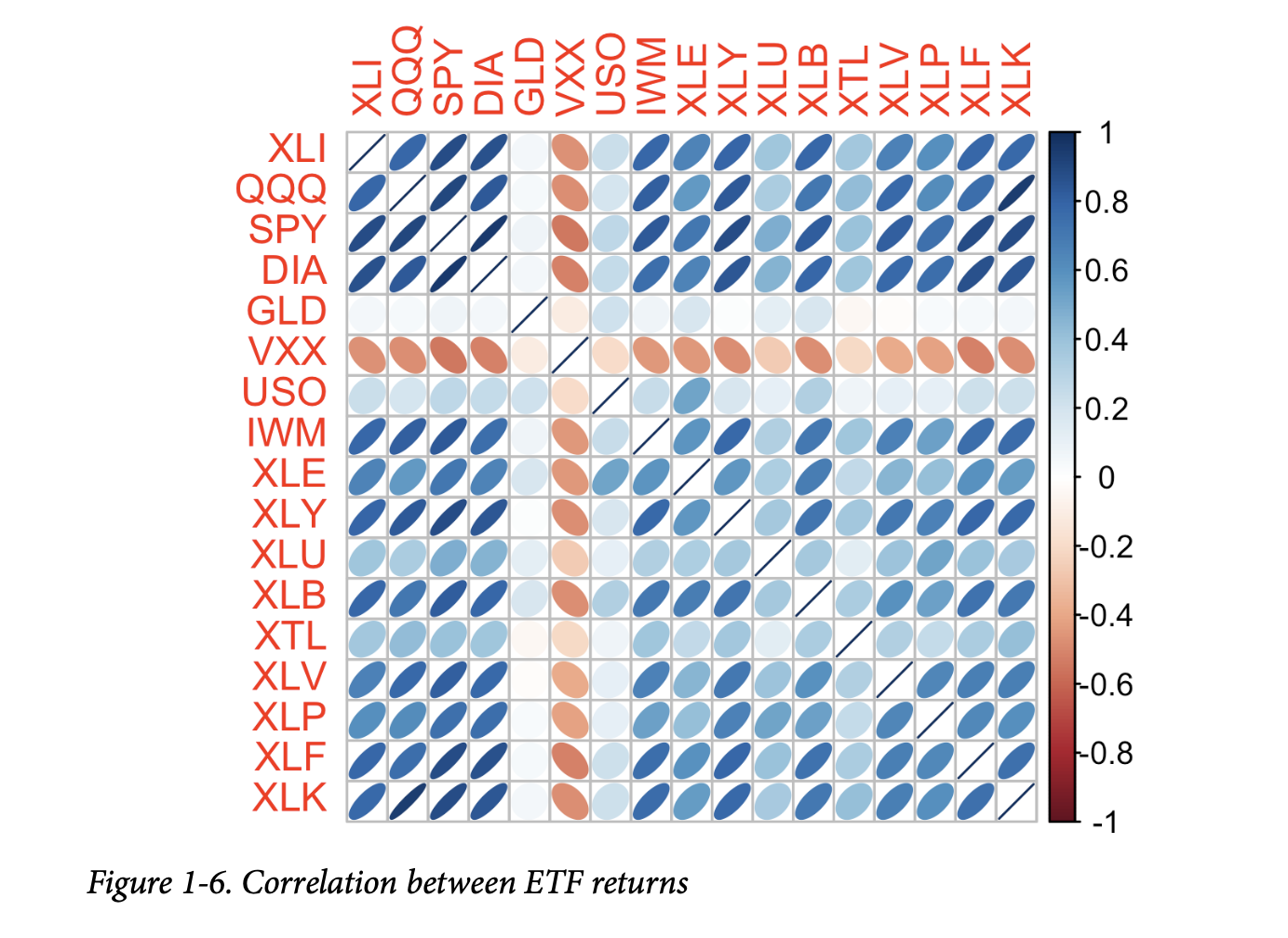
像表1-7这样的相关表通常被绘制出来，以视觉化地展示多个变量之间的关系。图1-6显示了主要交易所交易基金（ETF）日收益之间的相关性。在R中，我们可以使用 corrplot 包轻松创建：

1
2
3
4
etfs <- sp500_px[row.names(sp500_px) > '2012-07-01',
sp500_sym[sp500_sym$sector == 'etf', 'symbol']]
library(corrplot)
corrplot(cor(etfs), method='ellipse')

在Python中也可以创建相同的图，但常用包中没有现成的实现。然而，大多数都支持使用热图来可视化相关矩阵。以下代码演示了使用 seaborn.heat map 包的方法。在随附的源代码库中，我们包含了用于生成更全面的可视化的Python代码：

1
2
3
4
etfs = sp500_px.loc[sp500_px.index > '2012-07-01',
sp500_sym[sp500_sym['sector'] == 'etf']['symbol']]
sns.heatmap(etfs.corr(), vmin=-1, vmax=1,
cmap=sns.diverging_palette(20, 220, as_cmap=True))

标准普尔500指数ETF（SPY）和道琼斯指数ETF（DIA）具有较高的相关性。同样，主要由科技公司组成的QQQ和XLK也呈正相关。防御性ETF，例如那些追踪黄金价格（GLD）、石油价格（USO）或市场波动率（VXX）的ETF，倾向于与其它ETF弱相关或负相关。椭圆的方向表明两个变量是正相关（椭圆指向右上）还是负相关（椭圆指向左上）。椭圆的阴影和宽度表示关联的强度：越薄、越深的椭圆对应着越强的关系。

与均值和标准差一样，相关系数对数据中的异常值敏感。软件包提供了经典相关系数的稳健替代品。例如，R包 robust 使用 covRob 函数来计算相关性的稳健估计。scikit-learn 模块 sklearn.covariance 中的方法实现了多种方法。

知识点：

其他相关性估计

统计学家很久以前就提出了其他类型的相关系数，例如斯皮尔曼's \(\rho\)（rho）或肯德尔's \(\tau\)（tau）。这些是基于数据秩的相关系数。由于它们使用秩而不是值，这些估计量对异常值是稳健的，并且可以处理某些类型的非线性。然而，数据科学家通常可以坚持使用皮尔逊相关系数及其稳健替代品来进行探索性分析。基于秩的估计的吸引力主要在于较小的数据集和特定的假设检验。

散点图

Scatterplots

可视化两个测量数据变量之间关系的标准方法是使用散点图。x轴代表一个变量，y轴代表另一个变量，图上的每个点都是一个记录。图1-7显示了美国电话电报公司（ATT）和威瑞森（Verizon）日收益之间相关性的图。这在 R 中使用以下命令生成：

1
plot(telecom$T, telecom$VZ, xlab='ATT (T)', ylab='Verizon (VZ)')

使用 pandas 的 scatter 方法可以在 Python 中生成相同的图：

1
2
3
4
5
ax = telecom.plot.scatter(x='T', y='VZ', figsize=(4, 4), marker='$\u25EF$')
ax.set_xlabel('ATT (T)')
ax.set_ylabel('Verizon (VZ)')
ax.axhline(0, color='grey', lw=1)
ax.axvline(0, color='grey', lw=1)

收益之间存在正向关系：虽然它们聚集在零点附近，但在大多数日子里，两只股票同步上涨或下跌（右上和左下象限）。很少有一天是一只股票显著下跌而另一只股票上涨，反之亦然（右下和左上象限）。

F1.7

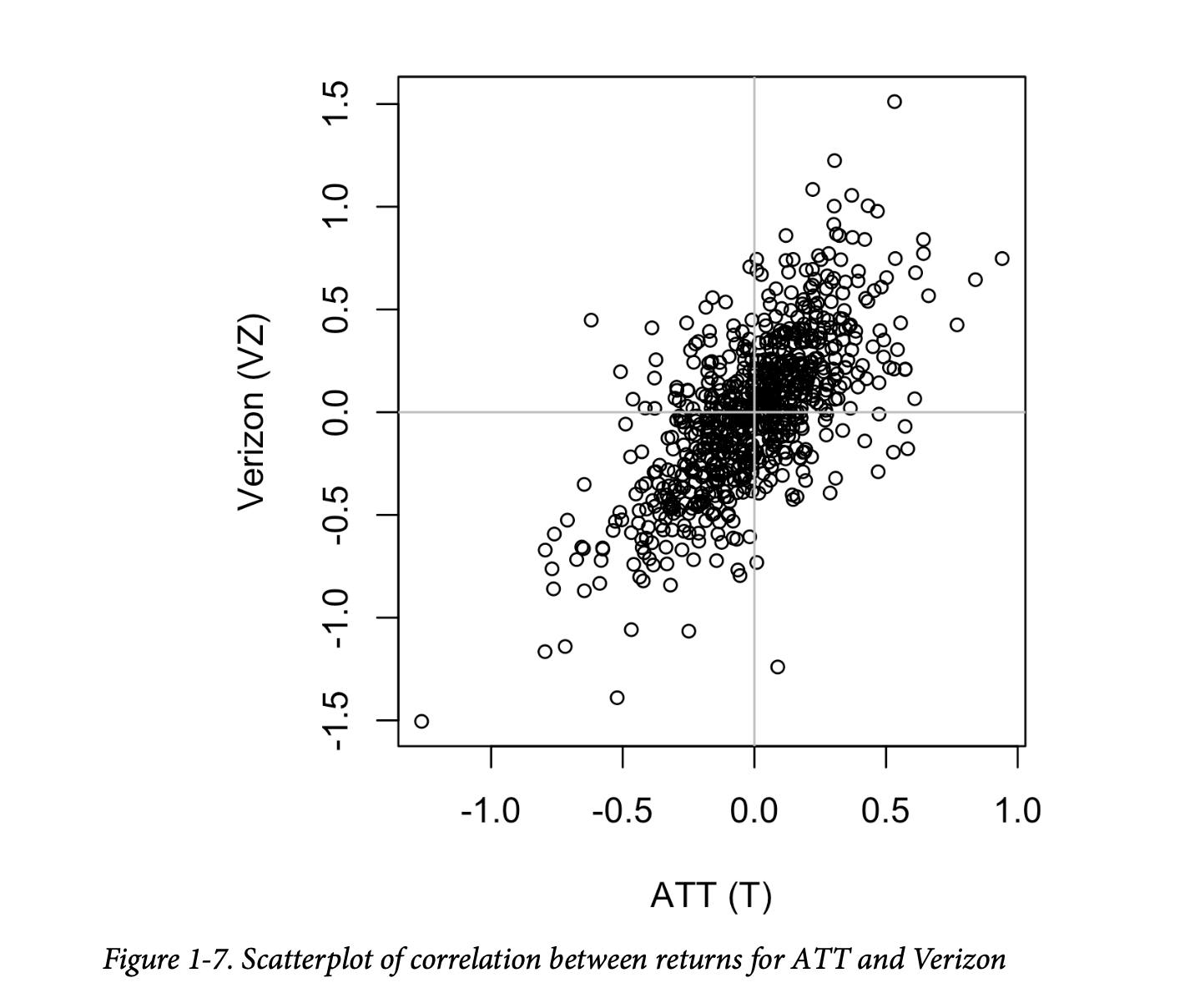
虽然图1-7只显示了754个数据点，但很明显，要识别图中中心的细节有多么困难。我们将在后面看到，如何通过增加点的透明度，或使用六边形分箱和密度图来帮助发现数据中的额外结构。

关键思想

  • 相关系数衡量两个成对变量（例如，个人的身高和体重）彼此关联的程度。
  • 当 v1 的高值伴随着 v2 的高值时，v1 和 v2 正相关。
  • 当 v1 的高值伴随着 v2 的低值时，v1 和 v2 负相关。
  • 相关系数是一个标准化度量，因此它始终在 -1（完全负相关）到 +1（完全正相关）之间。
  • 相关系数为零表示没有相关性，但要注意，数据的随机排列仅凭偶然性就会产生正值和负值的相关系数。

探索两个或多个变量

Exploring Two or More Variables

我们所熟悉的估计量，如均值和方差，每次都只考察一个变量（单变量分析）。相关性分析（参见第30页的“相关性”）是一种重要的比较两个变量（双变量分析）的方法。在本节中，我们将探讨额外的估计量和图表，以及超过两个变量的情况（多变量分析）。

探索两个或多个变量的关键术语

  • 列联表（Contingency table） 两个或多个类别变量之间的计数。
  • 六边形分箱（Hexagonal binning） 一种图，将两个数值变量的记录分箱到六边形中。
  • 等高线图（Contour plot） 一种像地形图一样显示两个数值变量密度的图。
  • 小提琴图（Violin plot） 类似于箱线图，但显示的是密度估计。

与单变量分析一样，双变量分析既包括计算汇总统计量，也包括生成可视化显示。适当的双变量或多变量分析类型取决于数据的性质：数值型还是类别型。

六边形分箱和等高线图

（绘制数值型 vs. 数值型数据）

Hexagonal Binning and Contours

(Plotting Numeric Versus Numeric Data)

当数据值相对较少时，散点图很好用。图1-7中的股票收益图只涉及大约750个点。对于拥有数十万或数百万条记录的数据集，散点图会过于密集，因此我们需要一种不同的方式来可视化这种关系。为了说明这一点，考虑 kc_tax 数据集，其中包含华盛顿州金县住宅的税收评估价值。为了专注于数据的主要部分，我们使用 subset 函数去除了非常昂贵、非常小或非常大的住宅：

1
2
3
4
kc_tax0 <- subset(kc_tax, TaxAssessedValue < 750000 &
SqFtTotLiving > 100 &
SqFtTotLiving < 3500)
nrow(kc_tax0)
1
[1] 432693

在pandas中，我们按以下方式筛选数据集：

1
2
3
4
kc_tax0 = kc_tax.loc[(kc_tax.TaxAssessedValue < 750000) &
(kc_tax.SqFtTotLiving > 100) &
(kc_tax.SqFtTotLiving < 3500), :]
kc_tax0.shape
1
(432693, 3)

F1.8

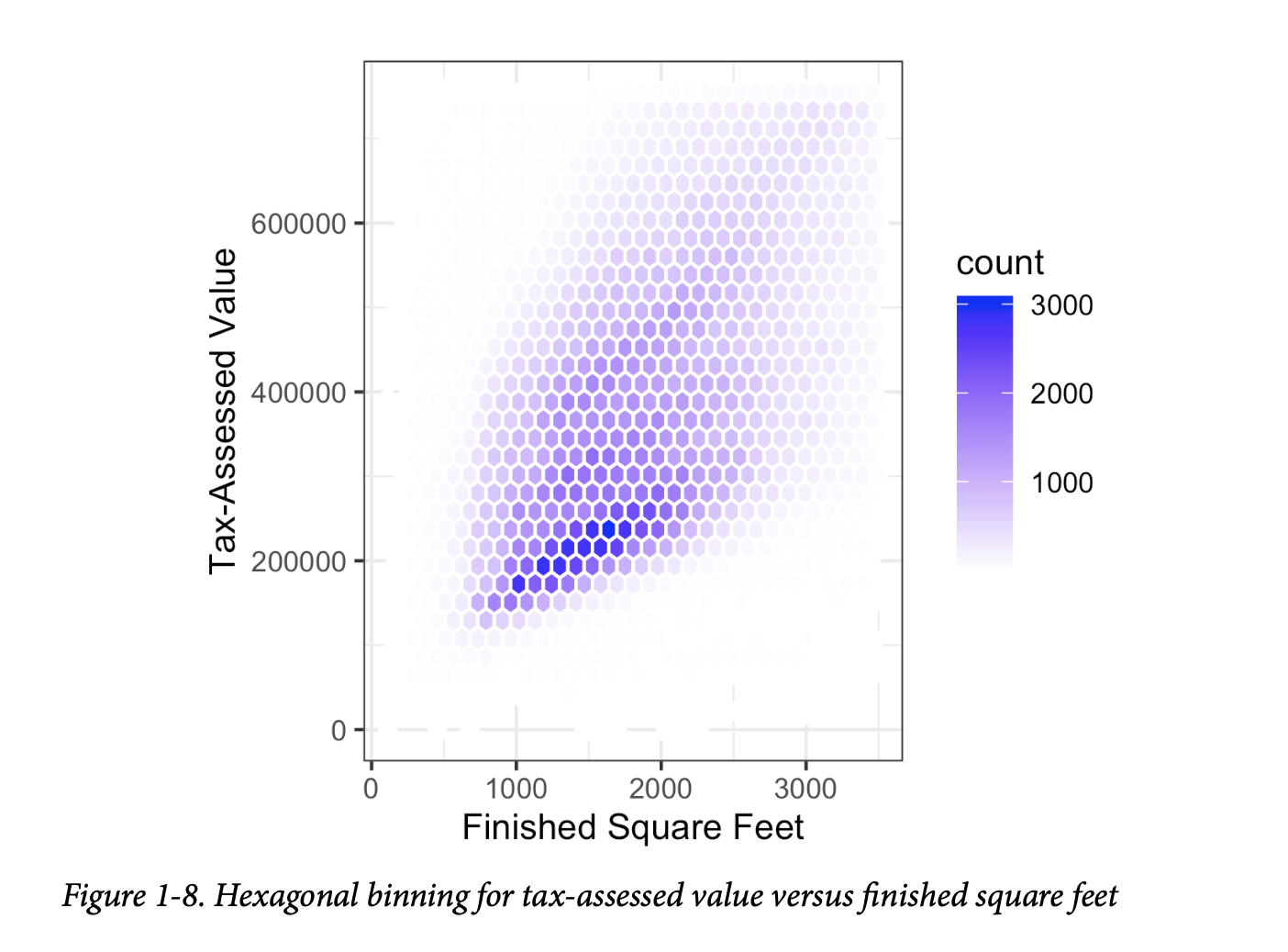
图1-8是金县住宅的已完成居住面积和税收评估价值之间关系的六边形分箱图。我们没有绘制点（这会像一个整体的黑云），而是将记录分组到六边形箱中，并用颜色绘制这些六边形，颜色表示该箱中的记录数量。在这张图中，平方英尺和税收评估价值之间的正向关系是清晰的。一个有趣的特征是，在底部的主（最暗）带上方隐约可见额外的条带，这表明这些住宅与主带中的住宅具有相同的居住面积，但税收评估价值更高。

图1-8由 Hadley Wickham 开发的强大 R 包 ggplot2 生成 [ggplot2]。ggplot2 是几个用于数据高级探索性视觉分析的新软件库之一；请参见第43页的“可视化多个变量”：

1
2
3
4
5
ggplot(kc_tax0, (aes(x=SqFtTotLiving, y=TaxAssessedValue))) +
stat_binhex(color='white') +
theme_bw() +
scale_fill_gradient(low='white', high='black') +
labs(x='Finished Square Feet', y='Tax-Assessed Value')

在 Python 中，使用 pandas 数据框方法 hexbin 可以轻松获得六边形分箱图：

1
2
3
4
ax = kc_tax0.plot.hexbin(x='SqFtTotLiving', y='TaxAssessedValue',
gridsize=30, sharex=False, figsize=(5, 4))
ax.set_xlabel('Finished Square Feet')
ax.set_ylabel('Tax-Assessed Value')

F1.9

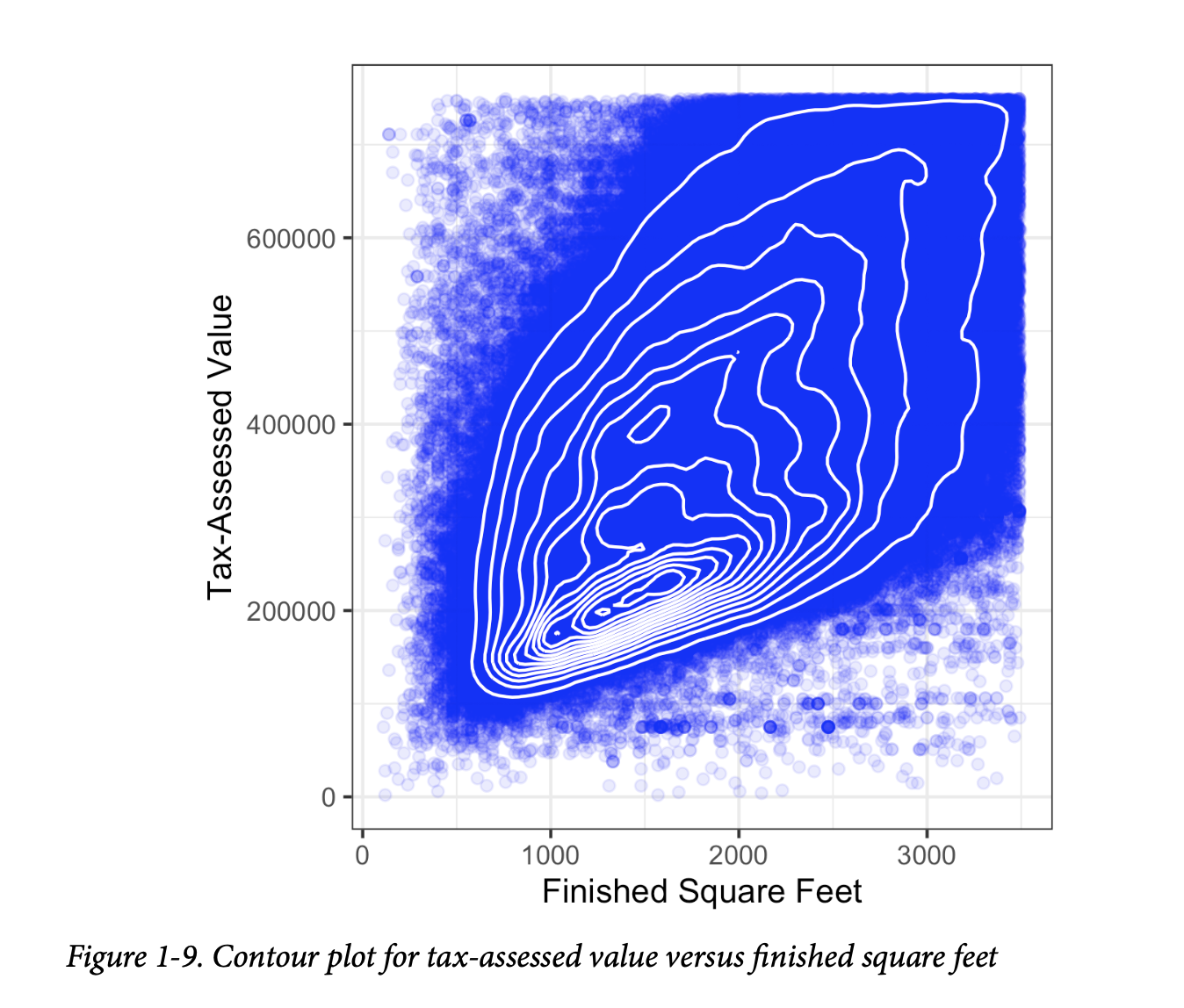
图1-9使用等高线叠加在散点图上，以可视化两个数值变量之间的关系。这些等高线本质上是两个变量的地形图；每个等高线带代表一个特定的点密度，当靠近“峰值”时密度会增加。这张图显示了与图1-8类似的情况：在主峰值的“北方”有一个次要峰值。这张图也是使用 ggplot2 和内置的 geom_density2d 函数创建的：

1
2
3
4
5
ggplot(kc_tax0, aes(SqFtTotLiving, TaxAssessedValue)) +
theme_bw() +
geom_point(alpha=0.1) +
geom_density2d(color='white') +
labs(x='Finished Square Feet', y='Tax-Assessed Value')

Python中的 seaborn 包 kdeplot 函数创建等高线图：

1
2
3
ax = sns.kdeplot(kc_tax0.SqFtTotLiving, kc_tax0.TaxAssessedValue, ax=ax)
ax.set_xlabel('Finished Square Feet')
ax.set_ylabel('Tax-Assessed Value')

还有其他类型的图表用于显示两个数值变量之间的关系，包括热图。热图、六边形分箱和等高线图都提供了二维密度的视觉表示。从这个意义上说，它们是直方图和密度图的自然类比。

两个类别变量

Two Categorical Variables

T1.8

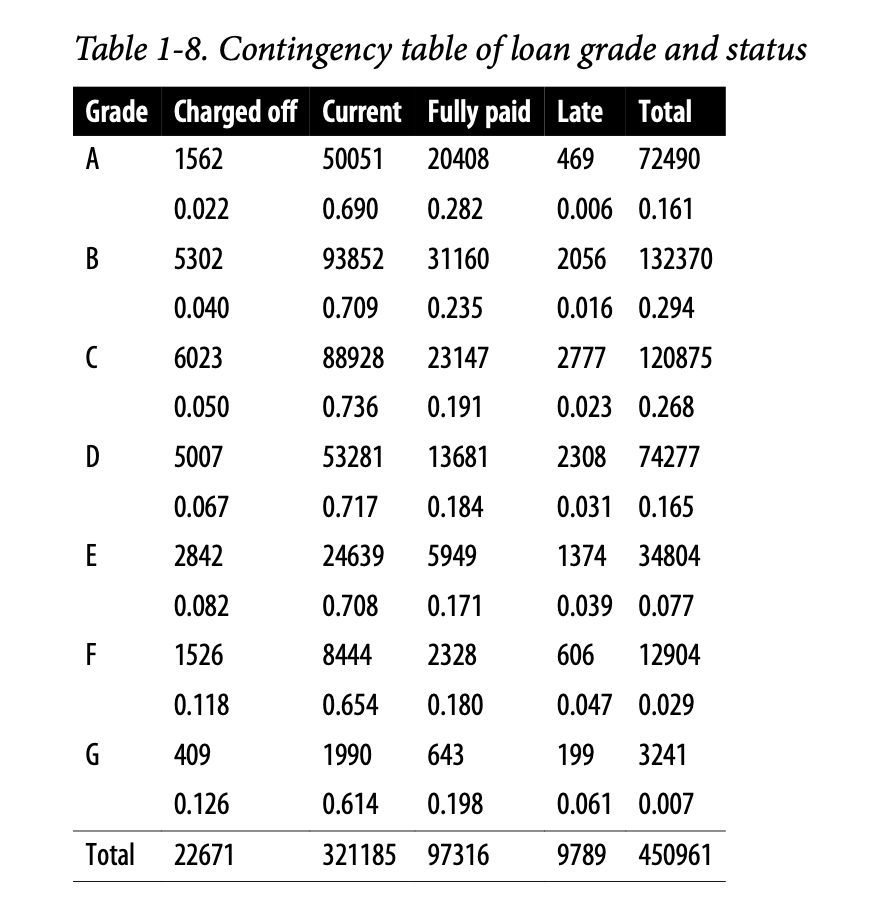
汇总两个类别变量的一种有用方法是列联表（contingency table）——一个按类别划分的计数表。表1-8显示了个人贷款的评级和该贷款的结果之间的列联表。这取自点对点借贷行业的领导者 Lending Club 提供的数据。评级从A（高）到G（低）。结果要么是全额偿付（fully paid）、当前（current）、逾期（late），要么是核销（charged off）（不期望收回贷款余额）。该表显示了计数和行百分比。与低评级贷款相比，高评级贷款的逾期/核销百分比非常低。

列联表可以只看计数，也可以包括列和总百分比。Excel中的数据透视表可能是用于创建列联表的最常用工具。在 R 中，descr 包中的 CrossTable 函数可以生成列联表，以下代码用于创建表1-8：

1
2
3
library(descr)
x_tab <- CrossTable(lc_loans$grade, lc_loans$status,
prop.c=FALSE, prop.chisq=FALSE, prop.t=FALSE)

pivot_table 方法在 Python 中创建数据透视表。aggfunc 参数允许我们获得计数。计算百分比稍微复杂一些：

1
2
3
4
5
6
7
crosstab = lc_loans.pivot_table(index='grade', columns='status',
aggfunc=lambda x: len(x), margins=True)
df = crosstab.loc['A':'G',:].copy()
df.loc[:,'Charged Off':'Late'] = df.loc[:,'Charged Off':'Late'].div(df['All'],
axis=0)
df['All'] = df['All'] / sum(df['All'])
perc_crosstab = df

margins 关键字参数将添加列和行总和。 我们创建数据透视表的副本，忽略列总和。 我们用行总和除以行。 我们将“All”列除以它的总和。

类别数据和数值数据

Categorical and Numeric Data

F1.10

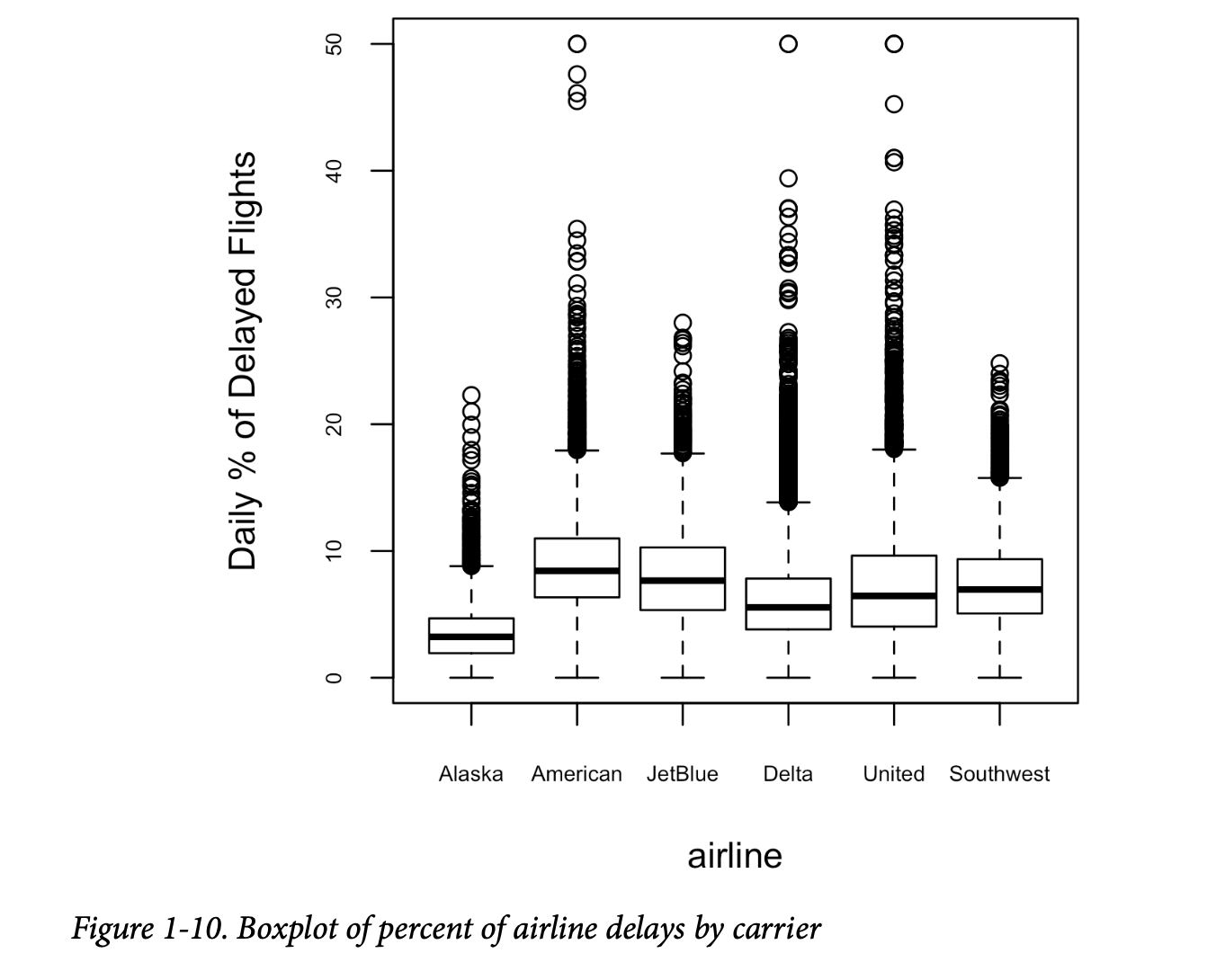
箱线图（参见第20页的“百分位数和箱线图”）是一种简单的方法，用于直观地比较根据类别变量分组的数值变量的分布。例如，我们可能想比较航班延误的百分比在不同航空公司之间有何差异。图1-10显示了一个月内，由于航空公司自身可控因素导致的航班延误百分比：

1
boxplot(pct_carrier_delay ~ airline, data=airline_stats, ylim=c(0, 50))

pandas 的 boxplot 方法接受 by 参数，该参数将数据集分成组并创建单独的箱线图：

1
2
3
4
ax = airline_stats.boxplot(by='airline', column='pct_carrier_delay')
ax.set_xlabel('')
ax.set_ylabel('Daily % of Delayed Flights')
plt.suptitle('')

阿拉斯加航空以延误最少而脱颖而出，而美国航空延误最多：美国航空的下四分位数高于阿拉斯加航空的上四分位数。

由 [Hintze-Nelson-1998] 引入的小提琴图是对箱线图的增强，它将密度估计与 y 轴上的密度一起绘制。密度被镜像并翻转，填充形成的形状，创造出类似小提琴的图像。小提琴图的优点是它可以显示箱线图中不明显的分布细微差别。另一方面，箱线图更清晰地显示了数据中的异常值。在 ggplot2 中，geom_violin 函数可用于创建小提琴图，如下所示：

1
2
3
4
ggplot(data=airline_stats, aes(airline, pct_carrier_delay)) +
ylim(0, 50) +
geom_violin() +
labs(x='', y='Daily % of Delayed Flights')

小提琴图可以使用 seaborn 包的 violinplot 方法获得：

1
2
3
4
ax = sns.violinplot(airline_stats.airline, airline_stats.pct_carrier_delay,
inner='quartile', color='white')
ax.set_xlabel('')
ax.set_ylabel('Daily % of Delayed Flights')

F1.11

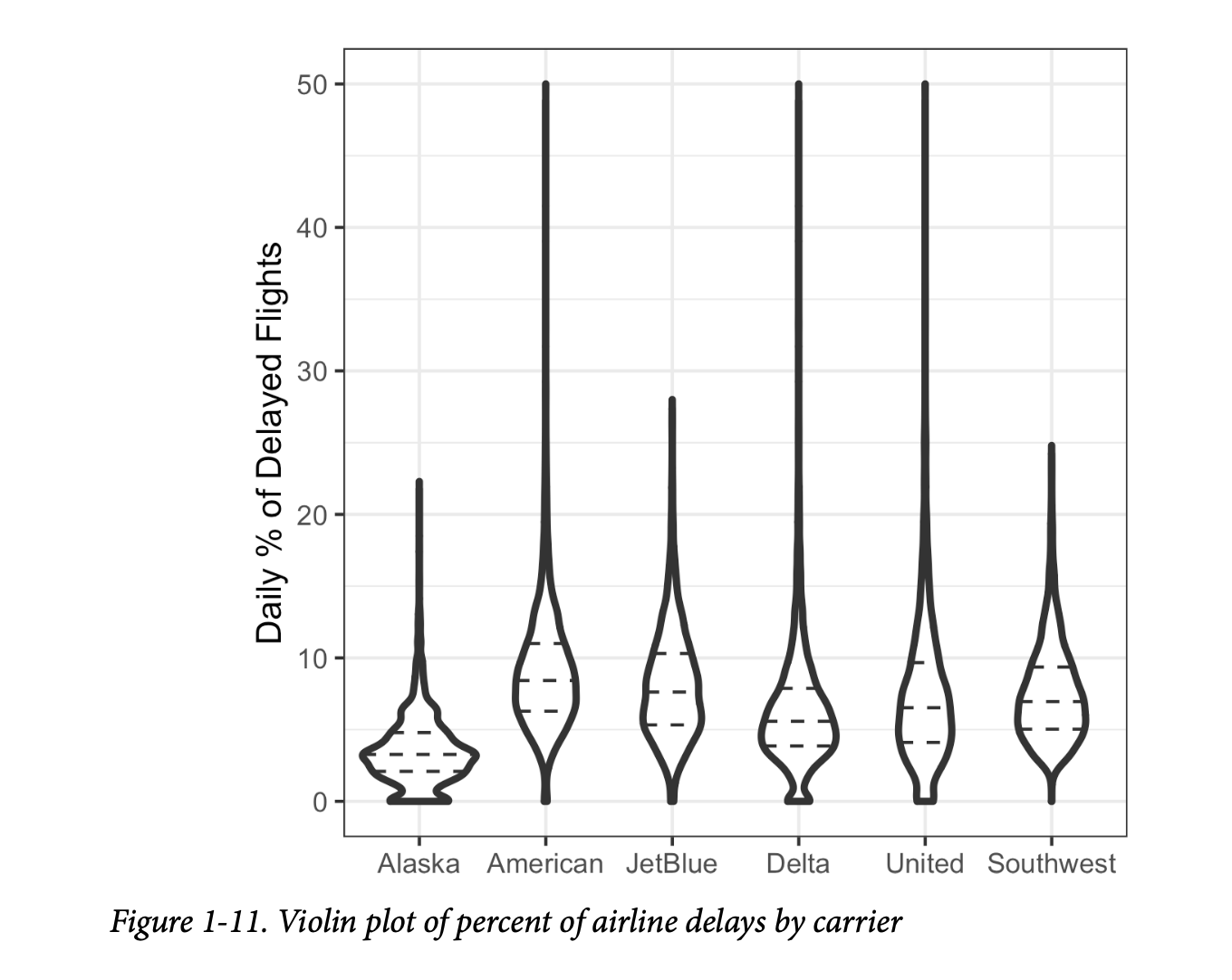
相应的图如图1-11所示。小提琴图显示，阿拉斯加航空以及程度较轻的达美航空，其分布集中在零点附近。这种现象在箱线图中不那么明显。您可以通过在绘图中添加 geom_boxplot 将小提琴图与箱线图结合起来（尽管这在使用颜色时效果最佳）。

可视化多个变量

Visualizing Multiple Variables

用于比较两个变量的图表类型——散点图、六边形分箱和箱线图——可以很容易地通过条件化（conditioning）的概念扩展到更多的变量。作为一个例子，回顾图1-8，它展示了房屋的已完成居住面积和其税收评估价值之间的关系。我们观察到，似乎有一群房屋每平方英尺的税收评估价值更高。深入挖掘，图1-12通过绘制一组邮政编码的数据来解释位置的影响。现在情况清晰得多：一些邮政编码（98105, 98126）的税收评估价值比其他邮政编码（98108, 98188）高得多。这种差异导致了在图1-8中观察到的聚类。

F1.12

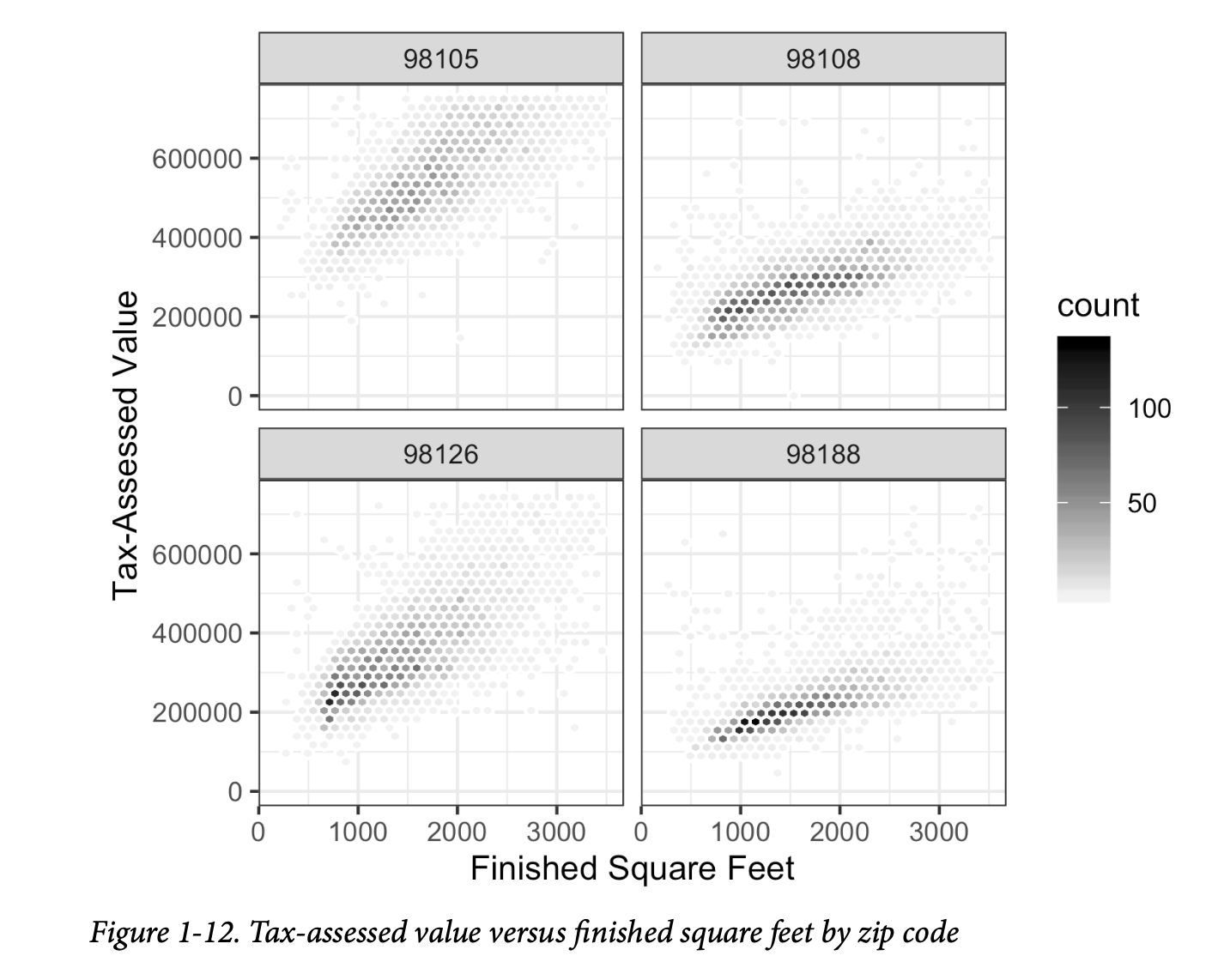
我们使用 ggplot2 和分面（facets）或条件化变量（conditioning variable）（在本例中为邮政编码）的概念创建了图1-12：

1
2
3
4
5
6
7
ggplot(subset(kc_tax0, ZipCode %in% c(98188, 98105, 98108, 98126)),
aes(x=SqFtTotLiving, y=TaxAssessedValue)) +
stat_binhex(color='white') +
theme_bw() +
scale_fill_gradient(low='white', high='blue') +
labs(x='Finished Square Feet', y='Tax-Assessed Value') +
facet_wrap('ZipCode')

使用 ggplot 函数 facet_wrap 和 facet_grid 来指定条件化变量。

大多数 Python 包的可视化都基于 Matplotlib。虽然原则上可以使用 Matplotlib 创建分面图，但代码可能会变得很复杂。幸运的是，seaborn 有一种相对简单的方法来创建这些图：

1
2
3
4
5
6
7
8
9
10
11
12
13
zip_codes = [98188, 98105, 98108, 98126]
kc_tax_zip = kc_tax0.loc[kc_tax0.ZipCode.isin(zip_codes),:]
kc_tax_zip
def hexbin(x, y, color,
**kwargs):
cmap = sns.light_palette(color, as_cmap=True)
plt.hexbin(x, y, gridsize=25, cmap=cmap,
**kwargs)
g = sns.FacetGrid(kc_tax_zip, col='ZipCode', col_wrap=2)
g.map(hexbin, 'SqFtTotLiving', 'TaxAssessedValue',
extent=[0, 3500, 0, 700000])
g.set_axis_labels('Finished Square Feet', 'Tax-Assessed Value')
g.set_titles('Zip code {col_name:.0f}')

使用参数 col 和 row 来指定条件化变量。对于单个条件化变量，将 col 与 col_wrap 一起使用，以将分面图包装成多行。map 方法使用原始数据集中不同邮政编码的子集来调用 hexbin 函数。extent 定义了 x 和 y 轴的范围。

图形系统中的条件化变量概念由 Rick Becker、Bill Cleveland 等人在贝尔实验室开发的 Trellis graphics [Trellis-Graphics] 首创。这个想法已经传播到各种现代图形系统，例如 R 中的 lattice [lattice] 和 ggplot2 包，以及 Python 中的 seaborn [seaborn] 和 Bokeh [bokeh] 模块。条件化变量也是 Tableau 和 Spotfire 等商业智能平台不可或缺的一部分。随着巨大计算能力的出现，现代可视化平台已经远远超出了探索性数据分析的简陋开端。然而，半个世纪前发展起来的关键概念和工具（例如，简单的箱线图）仍然构成了这些系统的基础。

关键思想

  • 六边形分箱和等高线图是有用的工具，可以同时对两个数值变量进行图形化检查，而不会被海量数据所淹没。
  • 列联表是查看两个类别变量计数的标准工具。
  • 箱线图和小提琴图允许您将一个数值变量与一个类别变量进行绘图。

总结

由约翰·图基（John Tukey）首创的探索性数据分析（Exploratory data analysis）（EDA）为数据科学领域奠定了基础。EDA 的核心思想是：任何基于数据的项目，其第一步也是最重要的一步就是查看数据。通过汇总和可视化数据，您可以获得对项目的宝贵直觉和理解。

本章回顾了从简单度量（如位置和变异性的估计）到丰富的视觉显示（探索多个变量之间的关系，如图1-12所示）等各种概念。开源社区正在开发的各种工具和技术，结合 R 和 Python 语言的表现力，创造了大量探索和分析数据的方法。探索性分析应该成为任何数据科学项目的基石。