《机器学习的数学基础》读书笔记

发表于 2025-09-06 更新于 2025-09-10 分类于读书心得

原书《MATHEMATICS FOR MACHINE LEARNING》原书英文版
本书分两部分：

Part I：Mathematical Foundations
PartII：Central Machine Learning Problems

马斯克的第一性原理、评价一个好学生就说他概念很清晰。这些都指向了基本的理解概念的重要性；正是这本书的特点；不过因为在一本书里面讲解了很多概念，包括线性代数、解析几何、微积分、概率等，所以还是需要读者有一定的数学基础，同时有些时候需要借助ChatGPT等工具进行概念的理解。

本书把涉及机器学习的数学的概念梳理了一遍；以介绍概念为主，从数学的角度、用数学的语言，从概念的角度引申出各知识点。这本书的优点是把涉及机器学习部分的数学概念讲得系统并深入浅出，把各个概念之间的关联性讲得很透彻，整体性很强，而不是简单概念的罗列。

不过，学习就是理论联系实际的过程，学习概念然后实践（练习、看书、应用等等），在实践中会发现对概念理解不透彻的地方，回头去理解概念，然后得到升华。概念就譬如对人的定义，在中国你可能觉得人就是黄种人的样子，但当你出国发现欧洲人之后，你回头去看人的定义，会增加对人这个概念的理解。

这本书通过数学语言定义了很多概念，直指本质；例如向量、内积；很多定义推翻了我们常识中的一些认定，例如内积，之前的通常的认知都是点积，其实真正内积的内涵广泛得多，应用也广泛得多。

核心的概念内积！！！！！！！内积的定义以及从内积引申出的正定矩阵、范数、距离等概念。

数学是这个世界上最精确的语言！

本笔记结合原版和网上中文翻译做了笔记。

中文翻译收录在这个专栏（只翻译了数学基础这一部分。）：

https://binaryai.blog.csdn.net/article/details/115050415

不过，中文版的译作者修改和加了一些内容，例如例6.1中，就把$换成人民币¥；还有矩阵那里增加了分块矩阵的运算！还有最后一章节的“信息论”原书并没有。

注意函数和曲面的区别。详见《函数与曲面.md》

以下是本书的一些摘录。

导言

理解这些原理可以帮助创建新的机器学习解决方案，理解和调试现有方法，了解我们正在使用的方法的固有假设和局限性。

为直觉寻找词语

作为另一个关于词语是多么微妙的例子，有（至少）三种不同的方式来思考向量：向量作为数字数组（计算机科学观点），向量作为具有方向和大小的箭头（物理学观），以及向量作为一个服从加法和缩放的对象（数学观点）。

向量和矩阵的研究称为 线性代数（linear algebra）

相似度和距离的构造是 解析几何（analytic geometry） 的核心

不确定性的量化是 概率论（probability theory） 的范畴

为了训练机器学习模型，我们通常会找到最大化某些性能指标的参数。许多优化技术需要梯度的概念，它告诉我们搜索解决方案的方向。第 5 章是关于 向量微积分（vector calculus） 并详细介绍梯度的概念

线性代数

Linear Algebra

在形式化一些直观概念时，常见的方法是构造一组对象(符号)和一些操作这些对象的规则。这就是所谓的代数(algebra)。线性代数是研究向量以及使用某些确定的规则来操作向量的一门学科。我们许多人从学校里知道的向量被称为“几何向量”，通常用上方带一个小箭头的字母表示。

向量是特殊的对象，将它们相加并乘以标量产生的是另一个相同类型的对象。从抽象的数学来看，任何满足这两个性质的物体都可以被认为是向量。

线性方程求解

出于数值精度的原因，通常不建议计算逆或伪逆。因此，在下文中，我们将简要讨论求解线性方程组的其他方法。高斯消元法在计算行列式、检查向量集是否线性独立、计算矩阵的逆，计算矩阵的秩，和确定向量空间的基时起着重要作用。高斯消元法是一种直观而有建设性的方法来解决一个含成千上万变量的线性方程组。然而，对于具有数百万个变量的方程组，这是不切实际的，因为所需的运算量是按联立方程组的数量的立方增长的。在实践中，许多线性方程组都是通过定常迭代方法(stationary iterative methods)间接求解的，如Richardson方法、Jacobi方法、Gauß-Seidel方法和逐次超松弛方法，或Krylov子空间方法，如共轭梯度、广义最小残差或双共轭梯度。

群

群的概念，它包含一组元素和一个定义在这些元素上的操作，该操作可以保持集合的某些结构完整。 群在计算机科学中扮演着重要的角色。除了为集合上的运算提供一个基本框架外，它们还被大量应用于密码学、编码理论和图形学。

封闭性(Closure)
结合律(Associativity)
单位元(Neutral elemen)
逆元(Inverse element)

如果可交换运算顺序，是阿贝尔群( Abelian group）

个人注：很多时候交换律都不是必须的。

向量空间的定义太赞了，通过群的定义引出！

线性变换的定义

保持向量空间结构不变需满足:

\[ \forall x, y \in V\ \forall \lambda, \psi \in \mathbb{R} : \Phi(\lambda \mathbf{x} + \psi \mathbf{y}) = \lambda \Phi(\mathbf{x}) + \psi \Phi(\mathbf{y}). \]

我们可以把线性映射用矩阵(2.7.1节)表示。回想一下前面的内容：我们将向量集合用矩阵的列表示。在处理矩阵时，我们必须判断矩阵所表示的内容：是线性映射还是向量集合。

个人注：重点要理解变换矩阵、恒等变换（$\text{id}_V$）、基变换的概念！！！！

空间结构不变的定义：

从几何角度理解线性变换保持空间结构不变，可以帮助直观掌握线性变换的本质。

1、线性变换几何视角的理解

线性变换 $\Phi: V \to W$ 是一种映射，满足：

加法保持：$\Phi(\mathbf{x} + \mathbf{y}) = \Phi(\mathbf{x}) + \Phi(\mathbf{y})$

数乘保持：$\Phi(\lambda \mathbf{x}) = \lambda \Phi(\mathbf{x})$

这意味着：

1）直线映射为直线 任何向量空间中的直线（即所有形如 $\mathbf{v}_0 + t\mathbf{v}$ 的点集，其中 $t \in \mathbb{R}$）经过线性变换后，仍然是直线（或退化成一点）。换句话说，线性变换不会把直线扭曲成曲线。

2）原点保持不变 由于 $\Phi(\mathbf{0}) = \mathbf{0}$，线性变换一定把原点映射为原点。这保持了空间的“参考点”。

3）比例保持 对于任意标量 $\lambda$，线性变换保证拉伸或压缩比例保持。例如，$\mathbf{x}$ 拉伸两倍后变为 $2\mathbf{x}$，变换后也是变换 $\Phi(\mathbf{x})$ 的两倍：$\Phi(2\mathbf{x}) = 2\Phi(\mathbf{x})$。

4）平行保持 如果两条线在原空间平行，那么它们的像也平行（或者重合）。这是因为线性变换保持向量加法关系。

5）向量加法的几何含义保持 变换前后，向量的组合关系（比如三角形的顶点、平行四边形的形状）在变换后的空间里依然成立（尽管大小和方向可能改变）。

2、换句话说

线性变换是“刚性”变换的一个推广，它可以拉伸、压缩、旋转、反射空间，但不会产生弯曲或折叠，也不会“撕裂”空间结构。它保持了“直线”、“比例”、“原点”这些最基础的几何性质。

3、举个例子

旋转是线性变换，保持长度和角度（保持空间结构不变的同时还保持距离）。

缩放（拉伸/压缩）也是线性变换，改变大小但不改变“直线性”和“比例”。

投影是线性变换，把三维空间映射到二维平面，保持直线的映射，但改变维度和形状。

变换矩阵

注意变换矩阵的定义。transformation matrix；以及使用变换矩阵将相对于$V$的有序基的坐标映射到相对于$W$中有序基的坐标；以及后文提到的，为了简化变换矩阵，通过基变换的处理。

在矩阵和有限维向量空间之间的线性映射之间建立一个显式联系。

重点是理解线性变换和矩阵之间的本质联系！

相似矩阵

如果存在可逆矩阵 $\boldsymbol{P}$，使得 \[ \boldsymbol{D} = \boldsymbol{P}^{-1} \boldsymbol{A} \boldsymbol{P} \] 则称矩阵 $\boldsymbol{A}$ 与 $\boldsymbol{D}$ 是相似(Similarity)的（定义 2.22）。

恒等映射

$\mathrm{id}_V : V \to V,\ x \mapsto x$ 为 $V$ 中的恒等映射或单位自同构 (identity mapping or identity automorphism)。

通过改变基从而改变向量的的表示，这允许通过一个简单的变换矩阵直接计算实现。

基变换

重要的作用：同一个点，在不同的基的不同坐标表示！变换矩阵相当于坐标的映射（不同基）。

在第四章中，我们将利用基变换的概念来寻找一个基，使得自同态的变换矩阵有一个特别简单的（对角）形式。在第十章降维中，我们将利用基变换研究一个数据压缩问题，即找到一个基并在这个基上投影数据从而压缩数据，同时最小化压缩损失。

变量变换和基变换的矩阵区别

要分清楚基变换和变量变换的区别！不要混淆；两者得出的变换矩阵是不同的。

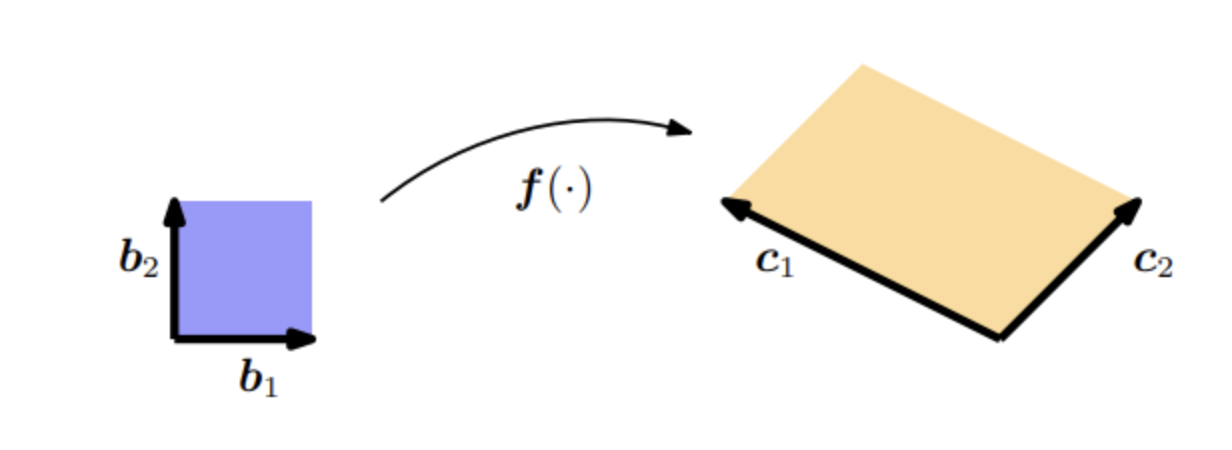
1、变量变换

如果给定两个向量 $\boldsymbol{b}_{1} = [1,0]^{\top}, \ \boldsymbol{b}_{2} = [0,1]^{\top}$ 作为单位正方形（图5.5中的蓝色区域）的边，则该正方形的面积为： \[ \left|\det\!\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\right| = 1 \]

如果我们取一个平行四边形（图5.5中的橙色区域），它的边为 $\boldsymbol{c}_{1} = [-2,1]^{\top}, \ \boldsymbol{c}_{2} = [1,1]^{\top}$，则它的面积是行列式（见第4.1节）的绝对值： \[ \left|\det\!\begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix}\right| = |-3| = 3 \]

即它的面积正好是单位方形的三倍。我们可以通过一个将单位方形转换成另一个方形的映射来找到这个缩放因子。用线性代数的术语说，就是有效地执行从 $(\boldsymbol{b}_{1}, \boldsymbol{b}_{2})$ 到 $(\boldsymbol{c}_{1}, \boldsymbol{c}_{2})$ 的变量变换。在我们的例子中，这个映射是线性的，且它的行列式的绝对值正好给出了我们要寻找的缩放因子。

因为$\boldsymbol{b}_{1},\boldsymbol{b}_{2}$是基，根据变换矩阵的定义，故变换矩阵是： \[ A = \begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix} \]

2、基变换

为了开始使用线性代数的方法，我们首先确定 $\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}$ 和 $\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}$ 都是 $\mathbb{R}^2$ 的基。我们要有效地执行的是从 $\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}$ 到 $\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}$ 的基变换，就得寻找实现基变换的变换矩阵。利用第2.7.2节的结果，我们确定了所需的基变换矩阵为： \[ \boldsymbol{J} = \begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix} \tag{5.62} \]

它使得 $\boldsymbol{J}\boldsymbol{b}_{1} = \boldsymbol{c}_{1}, \quad \boldsymbol{J}\boldsymbol{b}_{2} = \boldsymbol{c}_{2}$。矩阵 $\boldsymbol{J}$ 的行列式的绝对值为： \[ \left|\det(\boldsymbol{J})\right| = 3, \] 这正是我们在寻找的缩放因子。也就是说， $(\boldsymbol{c}_{1}, \boldsymbol{c}_{2})$ 所张成的平行四边形的面积是 $(\boldsymbol{b}_{1}, \boldsymbol{b}_{2})$ 所张成面积的三倍。

把 $\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}$ 坐标变换成 $\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}$ 的坐标，是左乘$\boldsymbol{J}^{-1}$；反向是左乘$\boldsymbol{J}$。

像与核

“直观地说，核是被 $\Phi$ 映射到单位元 $\mathbf{0}_W \in W$ 上的一组向量 $\mathbf{v} \in V$。”

具体见原书图2.12

F2.12

仿射空间

在下面，我们将研究从原点偏移的空间，即不再是向量子空间的空间。此外，我们将简要讨论这些仿射空间之间类似线性映射的一些性质。

备注：在机器学习领域的文献中，线性和仿射之间的区别有时是不明确的，因此我们可以将线性空间/映射作为仿射空间/映射的参考。

仿射映射

仿射映射保持几何结构不变。它们还保留了尺寸比例和平行度。

解析几何

Analytic Geometry

内积及其相应的范数和度量可以得到相似性和距离的直观概念

范数表示向量的长度，范数可以由内积引出，内积可以是不同的定义（所以不同的内积定义的长度是不一样的），内积由唯一的对称正定矩阵确定（正定矩阵的定义符合要求）。

用内积来计算向量的长度和向量之间的夹角.

范数

向量空间 $V$ 的范数是一个指定每个向量 $x$ 的长度的函数:

\[ \|\cdot\|: V \to \mathbb{R} \] \[ x \mapsto \|x\| \]

并且对于任何 $\lambda \in \mathbb{R}$ 以及 $x, y \in V$，以下成立：

绝对一次齐次性 (Absolutely homogeneous)：$\|\lambda x\| = |\lambda| \|x\|$
三角不等式 (Triangle inequality)：$\|x + y\| \leq \|x\| + \|y\|$
正定性 (Positive definite)：$|x| $ 且 $\|x\| = 0 \iff x = 0$

注意，范数可以是多种，例如$\mathcal l_1$范数（曼哈顿范数）、$\mathcal l_2$范数（欧氏距离）。

内积

内积可以引入一些直观的几何概念，例如向量的长度和两个向量之间的角度或距离。内积的一个主要目的是确定向量之间是否正交。

3.2.1 点积

我们可能已经熟悉了一种特殊类型的内积，$\mathbb{R}^n$中的标量积/点积（scalar product/dot product）：

\[ \mathbf{x}^\top \mathbf{y} = \sum_{i=1}^n x_i y_i \tag{3.5} \]

在这本书中，我们将把这种特殊的内积称为点积。但是，内积是具有特定性质的更一般的概念，我们现在将介绍这些概念。

定义 3.3：内积与内积空间

设 $V$ 为向量空间，$\langle \cdot,\cdot \rangle : V \times V \to \mathbb{R}$ 为一个双线性映射，即它将 $V$ 中两个向量映射为一个实数，则有：

若 $\langle \cdot,\cdot \rangle$ 是正定且对称的，则称其为 $V$ 上的内积，常记作 $\langle x, y \rangle$；
则 $(V, \langle \cdot,\cdot \rangle)$ 被称为一个内积空间（或带内积的实向量空间）；
若该内积为点积，则称 $(V, \langle \cdot,\cdot \rangle)$ 为一个欧氏向量空间。

注：本书将上述所有空间统称为“内积空间”。

注意：点积只是内积的一种特殊的定义，而非唯一。

注意，正定性是指$\forall \boldsymbol{x} \in V \setminus \{\mathbf{0}\}:\quad \boldsymbol{x}^{\top} \boldsymbol{A} \boldsymbol{x} > 0.$,而不是：$\boldsymbol{x}^T\boldsymbol{A} \boldsymbol{y} > 0.$

正定矩阵

正定矩阵一定是对称的。《正定矩阵和半正定矩阵的区别.md》

$A$ 正定 $\iff$ 所有特征值 $\lambda_i > 0$。（故行列式也大于0）

对称正定矩阵

对称正定矩阵在机器学习中起着重要的作用，它们是通过内积定义的。在 4.3 节矩阵分解中将涉及到对称正定矩阵。对称半正定矩阵的思想也是机器学习中核技巧的关键（12.4 节）。

考虑一个 $n$ 维向量空间 $V$ 和内积 \[ \langle \cdot, \cdot \rangle : V \times V \to \mathbb{R} \] （见定义 3.3），以及 $V$ 的有序基 \[ B = (\boldsymbol{b}_{1}, \ldots, \boldsymbol{b}_{n}). \] 对于合适的 $\psi_i, \lambda_j \in \mathbb{R}$，任何向量 $\boldsymbol{x}, \boldsymbol{y} \in V$ 都可以写成基向量的线性组合： \[ \boldsymbol{x} = \sum_{i=1}^{n} \psi_i \boldsymbol{b}_i \in V, \qquad \boldsymbol{y} = \sum_{j=1}^{n} \lambda_j \boldsymbol{b}_j \in V. \]

由于内积的双线性，对于所有 $\boldsymbol{x}, \boldsymbol{y} \in V$，有： \[ \langle \boldsymbol{x}, \boldsymbol{y} \rangle = \left\langle \sum_{i=1}^{n} \psi_i \boldsymbol{b}_i,\ \sum_{j=1}^{n} \lambda_j \boldsymbol{b}_j \right\rangle = \sum_{i=1}^{n}\sum_{j=1}^{n} \psi_i \langle \boldsymbol{b}_i, \boldsymbol{b}_j \rangle \lambda_j = \hat{\boldsymbol{x}}^{\top} \boldsymbol{A} \hat{\boldsymbol{y}}. \]

以 $n = 2$ 为例，考虑内积： \[ \left\langle \sum_{i=1}^{2} \psi_i \boldsymbol{b}_i, \sum_{j=1}^{2} \lambda_j \boldsymbol{b}_j \right\rangle = \left\langle \psi_1 \boldsymbol{b}_1 + \psi_2 \boldsymbol{b}_2,\ \lambda_1 \boldsymbol{b}_1 + \lambda_2 \boldsymbol{b}_2 \right\rangle = \psi_1 \left\langle \boldsymbol{b}_1, \lambda_1 \boldsymbol{b}_1 + \lambda_2 \boldsymbol{b}_2 \right\rangle + \psi_2 \left\langle \boldsymbol{b}_2, \lambda_1 \boldsymbol{b}_1 + \lambda_2 \boldsymbol{b}_2 \right\rangle. \]

展开后得到： \[ \begin{aligned} & \psi_1 [ \lambda_1 \langle \boldsymbol{b}_1, \boldsymbol{b}_1 \rangle + \lambda_2 \langle \boldsymbol{b}_1, \boldsymbol{b}_2 \rangle ] + \psi_2 [ \lambda_1 \langle \boldsymbol{b}_2, \boldsymbol{b}_1 \rangle + \lambda_2 \langle \boldsymbol{b}_2, \boldsymbol{b}_2 \rangle ] \\ &= [\psi_1, \psi_2] \begin{bmatrix} \langle \boldsymbol{b}_1, \boldsymbol{b}_1 \rangle & \langle \boldsymbol{b}_1, \boldsymbol{b}_2 \rangle \\ \langle \boldsymbol{b}_2, \boldsymbol{b}_1 \rangle & \langle \boldsymbol{b}_2, \boldsymbol{b}_2 \rangle \end{bmatrix} \begin{bmatrix} \lambda_1 \\ \lambda_2 \end{bmatrix} \\ &= [\psi_1, \psi_2]\, \boldsymbol{A} \begin{bmatrix} \lambda_1 \\ \lambda_2 \end{bmatrix}, \end{aligned} \] 其中 $A_{ij} := \langle \boldsymbol{b}_i, \boldsymbol{b}_j \rangle$，$\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}$ 为 $\boldsymbol{x}, \boldsymbol{y}$ 相对于基 $B$ 的坐标。这意味着内积 $\langle \cdot, \cdot \rangle$ 由 $\boldsymbol{A}$ 唯一确定。由于内积是对称的，矩阵 $\boldsymbol{A}$ 也是对称的。此外，内积的正定性意味着： \[ \forall \boldsymbol{x} \in V \setminus \{\mathbf{0}\}:\quad \boldsymbol{x}^{\top} \boldsymbol{A} \boldsymbol{x} > 0. \]

定义 3.4 对称正定矩阵

一个对称矩阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$ 称为对称正定矩阵（symmetric, positive definite），如果它满足： \[ \forall \boldsymbol{x} \in V \setminus \{\mathbf{0}\} : \quad \boldsymbol{x}^{\top} \boldsymbol{A} \boldsymbol{x} > 0. \]

如果只满足 \[ \forall \boldsymbol{x} \in V \setminus \{\mathbf{0}\} : \quad \boldsymbol{x}^{\top} \boldsymbol{A} \boldsymbol{x} \ge 0, \] 则称 $\boldsymbol{A}$ 为对称半正定矩阵（symmetric, positive semidefinite）。

例 3.4 对称正定矩阵

考虑矩阵 \[ \boldsymbol{A}_1 = \begin{bmatrix} 9 & 6 \\ 6 & 5 \end{bmatrix}, \quad \boldsymbol{A}_2 = \begin{bmatrix} 9 & 6 \\ 6 & 3 \end{bmatrix}. \]

对于任意 $\boldsymbol{x} = [x_1, x_2]^\top \neq \mathbf{0}$，有 \[ \boldsymbol{x}^{\top} \boldsymbol{A}_1 \boldsymbol{x} = [x_1, x_2] \begin{bmatrix} 9 & 6 \\ 6 & 5 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 9 x_1^2 + 12 x_1 x_2 + 5 x_2^2 = (3 x_1 + 2 x_2)^2 + x_2^2 > 0, \] 因此 $\boldsymbol{A}_1$ 是对称且正定的。而

\[ \boldsymbol{x}^{\top} \boldsymbol{A}_2 \boldsymbol{x} = 9 x_1^2 + 12 x_1 x_2 + 3 x_2^2 = (3 x_1 + 2 x_2)^2 - x_2^2, \] 当 $\boldsymbol{x} = [2, -3]^\top$ 时，$\boldsymbol{x}^{\top} \boldsymbol{A}_2 \boldsymbol{x} < 0$，所以 $\boldsymbol{A}_2$ 仅对称，但不是正定矩阵。

如果 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$ 是对称正定的，则可以定义内积： \[ \langle \boldsymbol{x}, \boldsymbol{y} \rangle = \hat{\boldsymbol{x}}^\top \boldsymbol{A} \hat{\boldsymbol{y}}, \] 其中 $\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}$ 为 $\boldsymbol{x}, \boldsymbol{y}$ 相对于有序基 $B$ 的坐标。

定理 3.5 对称正定矩阵与内积

设 $V$ 是一个实值、有限维向量空间，$B$ 是 $V$ 的一个有序基： \[ B = (\boldsymbol{b}_1, \ldots, \boldsymbol{b}_n), \] 并且 $\langle \cdot , \cdot \rangle : V \times V \to \mathbb{R}$ 是 $V$ 上的一个内积。

定理：内积 $\langle \cdot , \cdot \rangle$ 当且仅当存在一个对称正定矩阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$，使得对于任意 $\boldsymbol{x}, \boldsymbol{y} \in V$，有： \[ \langle \boldsymbol{x}, \boldsymbol{y} \rangle = \hat{\boldsymbol{x}}^\top \boldsymbol{A} \hat{\boldsymbol{y}}, \] 其中 $\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}$ 为 $\boldsymbol{x}, \boldsymbol{y}$ 相对于基 $B$ 的坐标向量。

如果 $\boldsymbol{A}$ 是对称正定矩阵，则它具有以下性质：

零空间（核）只包含零向量：对于所有 $\boldsymbol{x} \neq \mathbf{0}$，有 \[ \boldsymbol{x}^\top \boldsymbol{A} \boldsymbol{x} > 0, \] 这意味着如果 $\boldsymbol{x} \neq \mathbf{0}$，则 $\boldsymbol{A} \boldsymbol{x} \neq \mathbf{0}$。
对角元素为正：矩阵 $\boldsymbol{A}$ 的对角元素 $a_{ii}$ 满足 \[ a_{ii} = \boldsymbol{e}_i^\top \boldsymbol{A} \boldsymbol{e}_i > 0, \] 其中 $\boldsymbol{e}_i$ 是 $\mathbb{R}^n$ 的标准基向量

长度和距离

在第3.1节中，我们已经讨论了可以用来计算向量长度的范数。内积与范数密切相关，因为任何内积都自然地引出范数： \[ \|\boldsymbol{x}\| := \sqrt{\langle \boldsymbol{x}, \boldsymbol{x} \rangle} \] 这使得我们可以用内积来计算向量的长度。然而，并不是每一个范数都是由内积引起的。曼哈顿范数就是一种没有对应内积的范数。在下面，我们将集中讨论由内积导出的范数，并介绍一些几何概念，如长度、距离和角度。

柯西-施瓦兹不等式

对于一个内积向量空间 $(V, \langle \cdot, \cdot \rangle)$，其引出的范数 $\|\cdot\|$ 满足柯西-施瓦兹不等式（Cauchy-Schwarz Inequality）： \[ |\langle \boldsymbol{x}, \boldsymbol{y} \rangle| \leqslant \|\boldsymbol{x}\| \, \|\boldsymbol{y}\| \]

距离和度量

考虑一个内积空间 $(V, \langle \cdot, \cdot \rangle)$，对于任意 $\boldsymbol{x}, \boldsymbol{y} \in V$，定义： \[ d(\boldsymbol{x}, \boldsymbol{y}) := \|\boldsymbol{x} - \boldsymbol{y}\| = \sqrt{\langle \boldsymbol{x} - \boldsymbol{y}, \boldsymbol{x} - \boldsymbol{y} \rangle} \] 该式称为 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 之间的距离（distance）。如果我们采用点积（dot product）作为内积，则该距离被称为欧几里得距离（Euclidean distance）。定义映射： \[ d : V \times V \to \mathbb{R}, \quad (\boldsymbol{x}, \boldsymbol{y}) \mapsto d(\boldsymbol{x}, \boldsymbol{y}) \] 称为该空间上的一个度量（metric）。与向量的长度类似，向量之间的距离不一定需要依赖于内积：一般的范数已经足够用于定义距离。如果一个范数由内积引出，那么该范数导出的距离也依赖于所选用的内积，不同内积可能导致不同的距离定义。

乍一看，内积和度量的一系列属性看起来非常相似。然而，通过比较定义3.3和定义3.6，我们发现 $\langle \boldsymbol{x}, \boldsymbol{y} \rangle$ 和 $d(\boldsymbol{x}, \boldsymbol{y})$ 的表现是相反的：

当 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 非常相似时，其内积值较大，而度量值却很小（因为度量涉及两个向量的差，即 $\boldsymbol{x} - \boldsymbol{y}$）。

角度和正交

直观地说，两个向量之间的夹角告诉我们它们的方向有多相似。(个人注：和长度无关！)

两个向量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 是正交（orthogonal）的，当且仅当 \[ \langle \boldsymbol{x}, \boldsymbol{y} \rangle = 0, \] 写作 $\boldsymbol{x} \perp \boldsymbol{y}$。若 $\|\boldsymbol{x}\| = 1 = \|\boldsymbol{y}\|$，即两个向量都是单位向量，则称 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 为标准正交（orthonormal）的。

两个向量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 之间的角度 $\omega$ 取决于所采用的内积。关于一种内积正交的向量不一定关于其他内积正交。

夹角的定义：两个非零向量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 之间的夹角 $\omega$ 满足： \[ \cos \omega = \frac{\langle \boldsymbol{x}, \boldsymbol{y} \rangle}{\|\boldsymbol{x}\| \, \|\boldsymbol{y}\|} \]

正交矩阵

设方阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$。当且仅当 $\boldsymbol{A}$ 的列向量构成一组标准正交（orthonormal）的向量组时，$\boldsymbol{A}$ 被称为正交矩阵（orthogonal matrix）。

换句话说，$\boldsymbol{A}$ 是正交矩阵当且仅当满足： \[ \boldsymbol{A} \boldsymbol{A}^{\top} = \boldsymbol{I} = \boldsymbol{A}^{\top} \boldsymbol{A} \] 正交矩阵保持长度不变；正交矩阵变换是特殊的，因为当一个向量 $\boldsymbol{x}$ 被正交矩阵 $\boldsymbol{A}$ 变换后，其长度保持不变。以点积为内积时，可以如下推导： \[ \|\boldsymbol{A} \boldsymbol{x}\|^{2} = (\boldsymbol{A} \boldsymbol{x})^{\top} (\boldsymbol{A} \boldsymbol{x}) = \boldsymbol{x}^{\top} \boldsymbol{A}^{\top} \boldsymbol{A} \boldsymbol{x} = \boldsymbol{x}^{\top} \boldsymbol{I} \boldsymbol{x} = \boldsymbol{x}^{\top} \boldsymbol{x} = \|\boldsymbol{x}\|^{2} \] 因此，正交变换不会改变向量的长度或两向量之间的角度（即它保持内积结构），这使得正交矩阵广泛应用于几何变换、图像旋转、特征值分解等领域。这表明正交矩阵定义的变换是旋转（也可能是翻转）.

正交补：三维向量空间中的平面$U$可以由它的法向量来描述。法向量张成某子空间 $U$ 的正交补 $U^\perp$;在$n$维向量空间和仿射空间中，通常可以用正交补来描述超平面。

函数的内积

设两个函数 $\boldsymbol{u}: \mathbb{R} \rightarrow \mathbb{R}$ 与 $\boldsymbol{v}: \mathbb{R} \rightarrow \mathbb{R}$，则它们在区间 $[a, b]$ 上的内积可以定义为： \[ \langle u, v \rangle := \int_{a}^{b} u(x)\, v(x)\, dx, \quad \text{其中 } a, b < \infty \] 与一般的内积一样，我们可以使用这个定义来引出函数的范数和正交性。特别地，若$\langle u, v \rangle = 0,$则称函数 $u$ 和 $v$ 在该内积下是正交的。

一个例子：$\sin(x)$与 $\cos(x)$的正交性

若取函数 $u(x) = (x) $，$v(x) = (x) $，则$$ f(x) = u(x) v(x) = (x) (x) \[ 如图 3.8 所示，该函数是一个奇函数，即满足：$f(-x) = -f(x)$ 因此，在对称区间 $ [a, b] = [-\pi, \pi] $上，其积分为 0，即： \] _{-}^{} (x) (x), dx = 0 $$ 由此可知，$\sin(x)$与 $(x) $是正交函数。

如果积分区间为 $ [-, ] $，则下列函数集：$$ {1, (x), (2x), (3x), } $$ 构成一个正交函数集。也就是说，集合中任意两个不同的函数在该区间上的内积为 0。

该集合张成了一个函数的巨大子空间。这个子空间中的函数在 $ [-, ) $ 上是偶函数且具有周期性。将任意函数投影到这个子空间，是傅里叶级数（Fourier series）展开的核心思想。(备注：傅里叶级数中的正交函数集)

正交投影

投影是一类重要的线性变换（还有旋转和反射）。

投影（Projection）

设 $V $为一个向量空间，$U V $为 $V $ 的一个子空间。如果一个线性映射 $ : V U $满足：$$ ^2 = = , $$ 则称 $$是一个从 $ V $到 $U $的投影（projection）。

由于线性映射可以由矩阵表示，因此上述定义也适用于一类特殊的矩阵，这类矩阵被称为投影矩阵（projection matrix），记作 $ $，它满足：$$ ^2 = _ $$ 也就是说，投影矩阵是满足幂等性质（idempotent）的线性变换矩阵。投影 $\pi_{U}(\boldsymbol{x}) \in \mathbb{R}^{n}$ 仍然是 $n$ 维向量而不是标量。我们可以用张成子空间 $U$ 的基向量 $\boldsymbol{b}$ 来表示投影，这样我们就只需要一个坐标 $\lambda$ 来表示投影(针对一维子空间（线）上的投影)，而不再需要 $n$ 个坐标。在第四章矩阵分解中，我们将展示 $\pi_{U}(\boldsymbol{x})$ 是 $\boldsymbol{P}_{\pi}$ 的特征向量，对应的特征值为 $1$。

通过投影，我们可以近似求解无解的线性方程组 $ = $。线性方程组无解，意味着 $ $ 不在 $ $ 的张成空间中，也就是说，向量 $ $ 不在 $ $ 的列所张成的子空间内。具体的原理见资料《线性方程解的本质.md》文件。如果线性方程不能精确求解，那么我们可以尝试找到一个近似解（approximate solution）。其思想是在 $ $ 的列所张成的子空间中找到最接近 $ $ 的向量，即计算 $ $ 在 $ $ 的列所张成的子空间上的正交投影。这类问题在实践中经常出现，这个解叫做超定系统的最小二乘解（least-squares solution）（假设点积为内积）。

旋转

旋转(rotation)是一种线性映射（更具体地说，是欧氏向量空间的自同构），它将平面绕原点旋转$θ$角，即原点是一个不动点。

$\mathbb{R}^{2}$ 中，旋转使物体绕平面内的一个原点旋转。如果旋转角度是正的，我们就称为逆时针旋转。

在 $\mathbb{R}^{3}$ 中的旋转与 $\mathbb{R}^{2}$ 不同的是，在 $\mathbb{R}^{3}$ 中，我们可以围绕其中一维的轴旋转任何二维平面。确定通用旋转矩阵的最简单方法是确定标准基 $e_1, e_2, e_3$ 旋转得到的像，并确保这些像 $\boldsymbol{R e}_1, \boldsymbol{R e}_2, \boldsymbol{R e}_3$ 彼此正交。然后，我们可以通过组合标准基的像得到一个通用的旋转矩阵 $\boldsymbol{R}$

$\mathbb{R}^{n}$ 中的旋转：

从二维和三维推广到 $n$ 维的欧氏向量空间的旋转可以直观地描述为：固定其 $n-2$ 维，旋转 $\mathbb{R}^{n}$ 空间中的二维平面。就像在三维情况下，我们可以旋转任意平面（$\mathbb{R}^{n}$ 的二维子空间）。

旋转的性质:

旋转表现出许多有用的性质，这些性质可以通过将它们视为正交矩阵来说明（定义 3.8）：

旋转保持距离，即

\[ \|\boldsymbol{x} - \boldsymbol{y}\| = \left\| \boldsymbol{R}_{\theta}(\boldsymbol{x}) - \boldsymbol{R}_{\theta}(\boldsymbol{y}) \right\| \] 换句话说，任意两点经过旋转变换后，它们之间的距离保持不变。

旋转保持角度，即 $\boldsymbol{R}_{\theta} \boldsymbol{x}$ 和 $\boldsymbol{R}_{\theta} \boldsymbol{y}$ 之间的夹角与原始向量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 之间的夹角相同。
三维（或更高维）旋转通常是不可交换的。因此，应用旋转的顺序是重要的，即使它们是围绕同一点旋转。

在二维空间中，旋转是可交换的。也就是说，对于所有 $\phi, \theta \in [0, 2\pi)$，都有： \[ \boldsymbol{R}(\phi)\boldsymbol{R}(\theta) = \boldsymbol{R}(\theta)\boldsymbol{R}(\phi) \] 当且仅当它们围绕同一个点（例如原点）旋转时，二维旋转矩阵形成一个关于乘法的阿贝尔群。

矩阵分解

Matrix Decomposition

在本章中，我们将介绍矩阵的三个方面：如何概括矩阵，如何分解矩阵，以及如何利用矩阵分解进行矩阵近似，矩阵分解的一个类比是因数分解(factoring of numbers)。

对称正定矩阵的类平方根运算，即Cholesky分解。

行列式与迹

行列式只适用于方阵。
可以看作是将矩阵映射到一个实数的函数。
当且仅当行列式不等于0时，矩阵可逆。
上三角（下三角）矩阵的行列式是其对角元素的积。
行列式度量体积；列向量代表各条边。
一个方阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$ 的行列式 $\operatorname{det}(\boldsymbol{A}) \neq 0$，当且仅当 $\operatorname{rk}(\boldsymbol{A}) = n.$换句话说，$\boldsymbol{A}$ 可逆当且仅当它是满秩的

对于 $n \times n$ 矩阵的行列式，需要一个通用的算法来解决 $n > 3$ 的情况，我们将在下面探讨这个问题。定理 4.2 将计算 $n \times n$ 矩阵的行列式的问题简化为计算 $(n - 1) \times (n - 1)$ 矩阵的行列式。通过递归地应用拉普拉斯展开（Laplace Expansion），我们最终可以通过计算 $2 \times 2$ 矩阵的行列式来计算 $n \times n$ 矩阵的行列式。

行列式具有以下特性：

矩阵相乘的行列式是相应行列式的乘积，即 \[ \operatorname{det}(\boldsymbol{AB}) = \operatorname{det}(\boldsymbol{A}) \operatorname{det}(\boldsymbol{B}) \]
矩阵转置不改变行列式的值，即 \[ \operatorname{det}(\boldsymbol{A}) = \operatorname{det}(\boldsymbol{A}^{\top}) \]
如果 $\boldsymbol{A}$ 是正则的（可逆的）， \[ \operatorname{det}(\boldsymbol{A}^{-1}) = \frac{1}{\operatorname{det}(\boldsymbol{A})} \]
相似矩阵（定义 2.22）具有相同的行列式。因此，对于线性映射 $\Phi: V \rightarrow V$，$\Phi$ 的所有变换矩阵 $\boldsymbol{A}_\Phi$ 都具有相同的行列式。因此，线性映射基的选择不影响行列式的值。（注意前提是$V \rightarrow V$）
将一列/行的倍数加到另一列/行不会更改 $\operatorname{det}(\boldsymbol{A})$。
用标量 $\lambda \in \mathbb{R}$ 乘矩阵 $\boldsymbol{A}$ 的行/列，将 $\lambda$ 倍缩放 $\operatorname{det}(\boldsymbol{A})$。特别地， \[ \operatorname{det}(\lambda \boldsymbol{A}) = \lambda^n \operatorname{det}(\boldsymbol{A}) \]
交换两行/列将更改 $\operatorname{det}(\boldsymbol{A})$ 的符号。

迹

方阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$ 的迹（trace）定义为：

\[ \operatorname{tr}(\boldsymbol{A}) := \sum_{i=1}^{n} a_{ii} \]

即，迹是 $\boldsymbol{A}$ 的对角元素之和。

迹满足以下属性：

对于 $\boldsymbol{A}, \boldsymbol{B} \in \mathbb{R}^{n \times n}$，有： \[ tr⁡(A+B)== \operatorname{tr}(\boldsymbol{A}) + \operatorname{tr}(\boldsymbol{B}) \]
对于 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$，$\alpha \in \mathbb{R}$，有： \[ tr⁡(αA) = \alpha \operatorname{tr}({A}) \]
单位矩阵的迹为： \[ tr⁡(In) = n \]
对于 $\boldsymbol{A} \in \mathbb{R}^{n \times k}$，$\boldsymbol{B} \in \mathbb{R}^{k \times n}$，有： \[ tr⁡(AB)= \operatorname{tr}({B}{A}) \]

可以证明，只有一个函数同时满足这四个性质——即迹（Gohberg et al., 2012）。

线性映射的矩阵表示依赖于基，而线性映射$\phi$的迹独立于基。具体原理见资料《迹的相似不变性.md》

特征多项式:

将行列式和迹作为描述方阵的函数来讨论。

对于 $\lambda \in \mathbb{R}$ 和一个方阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$，其特征多项式（Characteristic Polynomial）定义为：

\[ p_A(\lambda) := \det(\boldsymbol{A} - \lambda \boldsymbol{I}) = c_0 + c_1 \lambda + c_2 \lambda^2 + \cdots + c_{n-1} \lambda^{n-1} + (-1)^n \lambda^n \]

其中 $c_0, \ldots, c_{n-1} \in \mathbb{R}$。特别地，

\[ c_0 = \det(\boldsymbol{A}), \quad c_{n-1} = (-1)^{n-1} \operatorname{tr}(\boldsymbol{A}) \]

特征多项式将允许我们计算特征值和特征向量。

特征值和特征向量

指向同一方向的两个向量称为共向的(codirected)。如果两个向量指向相同或相反的方向，则它们是共线的（collinear）。

令 $A \in \mathbb{R}^{n \times n}$ 为一个方阵。

\[ \boldsymbol{A}\boldsymbol{x} = \lambda \boldsymbol{x} \]

我们称这个方程为特征方程（eigenvalue equation）。其中 $\lambda \in \mathbb{R}$ 为 $\boldsymbol{A}$ 的特征值（eigenvalue），$\boldsymbol{x} \in \mathbb{R}^{n} \setminus \{\boldsymbol{0}\}$ 为相应的特征向量（eigenvector）。

如果 $A$ 不是方阵会发生什么？

设 $A \in \mathbb{R}^{m \times n}$，如果 $m \ne n$，则：

$\boldsymbol{x} \in \mathbb{R}^n$

$A\boldsymbol{x} \in \mathbb{R}^m$

无法比较 $A\boldsymbol{x}$ 与 $\lambda \boldsymbol{x}$，因为它们不在同一个空间中！

所以没有办法定义类似

$A\boldsymbol{x} = \lambda \boldsymbol{x}$

这种“成比例”的特征值概念。

以下说法是等效的：

$\lambda$ 是 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$ 的特征值。
存在 $\boldsymbol{x} \in \mathbb{R}^{n} \backslash \{\mathbf{0}\}$，使得 $\boldsymbol{A}\boldsymbol{x} = \lambda \boldsymbol{x},$ 或等价地 $ ( - _{n}) = $ 有非平凡解，即 $\boldsymbol{x} \neq \mathbf{0}$。
$ !( - _{n}) < n$
$ !( - _{n}) = 0$

特征空间和特征谱:

对于 $A \in \mathbb{R}^{n \times n}$，$\boldsymbol{A}$ 对应于特征值 $\lambda$ 的特征向量集合张成 $\mathbb{R}^{n}$ 的子空间，这个子空间称为 $\boldsymbol{A}$ 关于 $\lambda$ 的特征空间（eigenspace），记为：$E_{\lambda}$ ; $\boldsymbol{A}$ 的特征值构成的集合称为特征谱（eigenspectrum），或 $\boldsymbol{A}$ 的谱。

单位矩阵 $\boldsymbol{I} \in \mathbb{R}^{n \times n}$ 的特征方程为：

\[ P_{I}(\lambda) = \operatorname{det}(\boldsymbol{I} - \lambda \boldsymbol{I}) = (1 - \lambda)^n = 0 \]

它只拥有 $\lambda = 1$ 这个特征值，并出现 $n$ 次。而且，对于任意 $\boldsymbol{x} \in \mathbb{R}^{n} \setminus \{\boldsymbol{0}\}$，有：

\[ \boldsymbol{I} \boldsymbol{x} = \lambda \boldsymbol{x} = 1 \cdot \boldsymbol{x} \]

因此，单位矩阵的唯一特征空间 $E_1$ 张成 $n$ 维，$\mathbb{R}^{n}$ 的 $n$ 个标准基向量都是 $\boldsymbol{I}$ 的特征向量。

关于特征值和特征向量的常用特性包括：

矩阵 $\boldsymbol{A}$ 及其转置 $\boldsymbol{A}^{\top}$ 具有相同的特征值，但不一定具有相同的特征向量。
特征空间 $E_{\lambda}$ 是 $\boldsymbol{A} - \lambda \boldsymbol{I}$ 的零空间，因为：

\[ \boldsymbol{A} \boldsymbol{x} = \lambda \boldsymbol{x} \Longleftrightarrow \boldsymbol{A} \boldsymbol{x} - \lambda \boldsymbol{x} = \boldsymbol{0} \Longleftrightarrow (\boldsymbol{A} - \lambda \boldsymbol{I}) \boldsymbol{x} = \boldsymbol{0} \Longleftrightarrow \boldsymbol{x} \in \ker(\boldsymbol{A} - \lambda \boldsymbol{I}) \]

相似矩阵（定义 2.22）具有相同的特征值。基变换得到的是相似矩阵。因此，线性映射 $\Phi$ 的特征值与它的变换矩阵的基的选择无关。这使得特征值、行列式和迹成为线性映射的重要不变量。
对称正定矩阵总是有正的实特征值。

剪切映射：

剪切映射（Shearing Mapping） 是一种保持某些几何特征（如面积、体积）不变，但改变形状的线性变换。在二维或三维欧几里得空间中，它通过“滑动”坐标轴方向的某些分量，使图形在不旋转也不缩放的前提下发生倾斜变形。

几何直观：

剪切会把一个矩形变成平行四边形。

面积保持不变。

角度和形状会改变，但线之间的平行关系保持。

单位正方形在剪切后变成平行四边形，但底边长度不变。

详见《剪切映射的变换矩阵.md》

特征值为 0 的特征向量是矩阵零空间中的非零向量；它揭示了矩阵在某些方向上把向量“压扁”为零；

一个矩阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$ 的 $n$ 个特征向量 $\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{n}$ 对应 $n$ 个不同的特征值 $\lambda_{1}, \ldots, \lambda_{n}$，则它们是线性独立的。这个定理指出，具有 $n$ 个不同特征值的矩阵的特征向量构成 $\mathbb{R}^{n}$ 的一组基。

给定一个矩阵 $\boldsymbol{A} \in \mathbb{R}^{m \times n}$，我们总能通过$\boldsymbol{S} := \boldsymbol{A}^{\top} \boldsymbol{A}$ 得到一个对称的半正定矩阵$\boldsymbol{S} \in \mathbb{R}^{n \times n}$。

很多地方只需要半正定矩阵即可。

谱定理

Spectral Theorem

如果 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$ 是对称的，则存在 $\boldsymbol{A}$ 的特征向量组成向量空间 $V$ 的一个正交基，且每个特征值都是实数。

谱定理的直接含义是：对称矩阵 $\boldsymbol{A}$ 存在特征值分解（具有实特征值），并且我们可以由特征向量构造一个标准正交基，使得 \[ \boldsymbol{A} = \boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{\top}, \] 其中 $\boldsymbol{D}$ 是对角矩阵，$\boldsymbol{P}$ 的列是 $\boldsymbol{A}$ 的单位特征向量，满足 $\boldsymbol{P}^{\top} \boldsymbol{P} = \boldsymbol{I}$。

特征值、特征向量、行列式、迹的联系

定理 4.16：

设矩阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$，则其行列式等于其所有特征值的乘积，即 \[ \det(\boldsymbol{A}) = \prod_{i=1}^{n} \lambda_i \] 其中 $\lambda_i \in \mathbb{C}$（可重复）为矩阵 $\boldsymbol{A}$ 的特征值。

定理 4.17：

设矩阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$，则其迹等于其所有特征值的和，即 \[ \operatorname{tr}(\boldsymbol{A}) = \sum_{i=1}^{n} \lambda_i \] 其中 $\lambda_i \in \mathbb{C}$（可重复）为矩阵 $\boldsymbol{A}$ 的特征值。

矩阵分解

Matrix Decomposition

Cholesky分解

对称正定矩阵 $\boldsymbol{A}$ 可以分解为： \[ \boldsymbol{A} = \boldsymbol{L} \boldsymbol{L}^{\top}, \] 其中 $\boldsymbol{L}$ 是具有正对角元素的下三角矩阵。 $\boldsymbol{L}$ 被称为 $\boldsymbol{A}$ 的Cholesky 因子（Cholesky factor），且是唯一的。

特征值分解与对角化

矩阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$ 的对角化，实际是在另一个基中表示相同线性映射的一种方法，这个基由 $\boldsymbol{A}$ 的特征向量组成。

定理 4.20特征值分解，Eigendecomposition

设 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$，则当且仅当 $\boldsymbol{A}$ 有 $n$ 个线性无关的特征向量时，$\boldsymbol{A}$ 可以被对角化，即存在可逆矩阵 $\boldsymbol{P}$ 和对角矩阵 $\boldsymbol{D}$，使得： \[ \boldsymbol{A} = \boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{-1} \]

其中：$\boldsymbol{P} \in \mathbb{R}^{n \times n}$ 的列是 $\boldsymbol{A}$ 的 $n$ 个线性无关的特征向量；$\boldsymbol{D}$ 是对角矩阵，其对角元素为 $\boldsymbol{A}$ 的特征值（可重复）；因此，只有当 $\boldsymbol{A}$ 的特征向量张成 $\mathbb{R}^n$，即 $\boldsymbol{A}$ 是非亏损的，$\boldsymbol{A}$ 才可以对角化。

定理 4.21对称矩阵的特征值分解

设 $\boldsymbol{S} \in \mathbb{R}^{n \times n}$ 是对称矩阵（即 $\boldsymbol{S}^{\top} = \boldsymbol{S}$），则 $\boldsymbol{S}$ 一定可以被对角化。

根据谱定理，对于任意对称矩阵 $\boldsymbol{S}$，存在一个标准正交基，由 $\boldsymbol{S}$ 的特征向量构成。即存在正交矩阵 $\boldsymbol{P}$，使得：

\[ \boldsymbol{S} = \boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^\top \]

其中： - $\boldsymbol{P} \in \mathbb{R}^{n \times n}$ 是正交矩阵，列向量为单位正交的特征向量； - $\boldsymbol{D}$ 是对角矩阵，对角元素为 $\boldsymbol{S}$ 的特征值； - 此分解方式也可表示为 $\boldsymbol{D} = \boldsymbol{P}^\top \boldsymbol{S} \boldsymbol{P}$。

图解特征值分解

在相同的向量空间中应用相同的基变化，然后撤消。

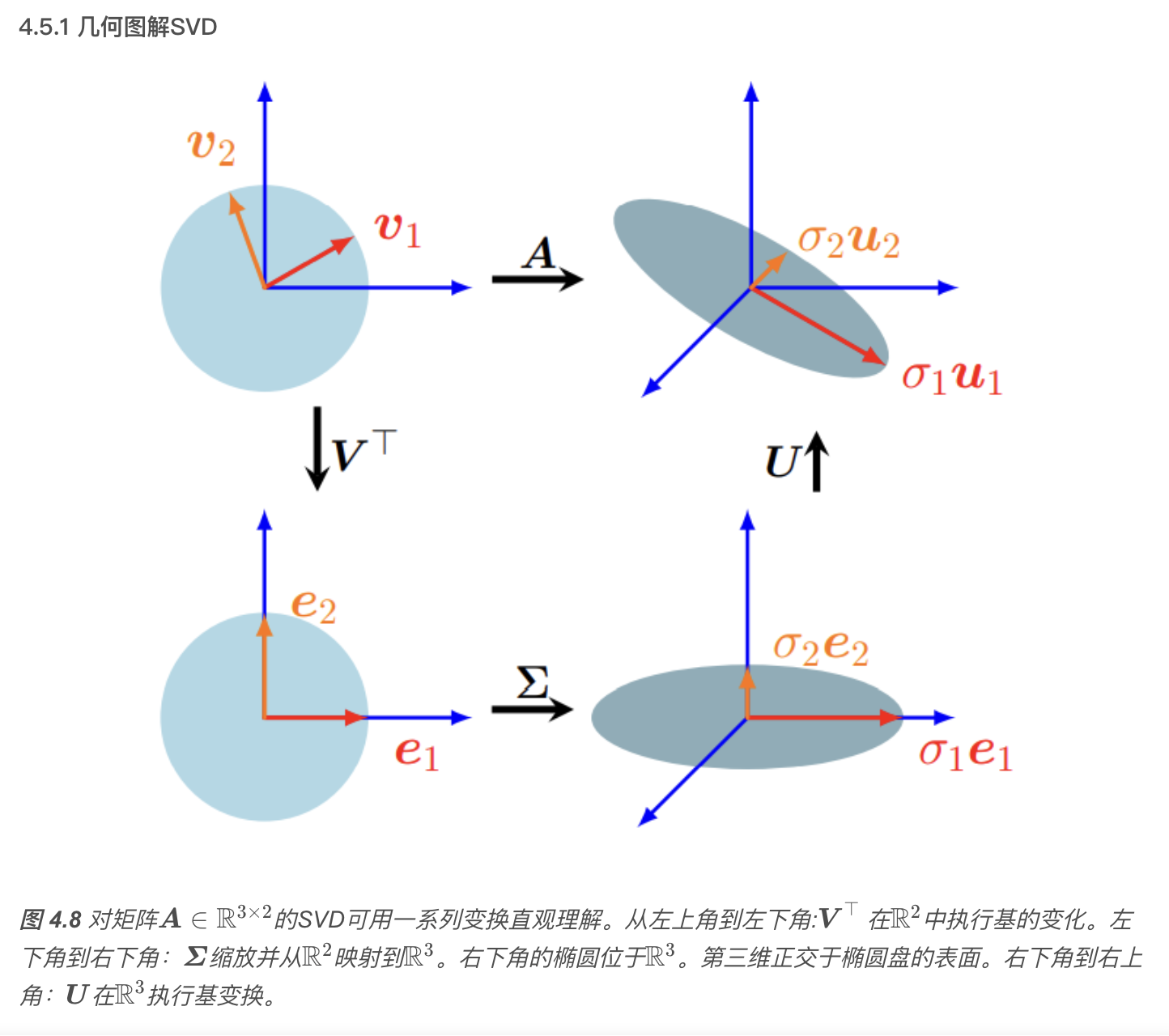
奇异值分解

singular value decomposition, SVD

表示线性映射 $\Phi: V \rightarrow W$ 的矩阵 $\boldsymbol{A}$ 的奇异值分解量化了这两个向量空间的潜在几何变化。

奇异值分解（SVD）公式

\[ \boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^\top \]

以及它在几何上的意义（旋转+缩放+旋转）.

其中 $\boldsymbol{U} \in \mathbb{R}^{m \times m}$ 为正交矩阵，其列向量为 $\boldsymbol{u}_i, \ i=1, \ldots, m$；$\boldsymbol{V} \in \mathbb{R}^{n \times n}$ 也为正交矩阵，其列向量为$\boldsymbol{v}_i, \ i=1, \ldots, n$。另外，$\boldsymbol{\Sigma}$ 为 $m \times n$ 矩阵，且$\Sigma_{ii} = \sigma_i \geqslant 0, \quad \Sigma_{ij} = 0, \ i \neq j .$ $\boldsymbol{\Sigma}$ 的对角元素$\sigma_i, \quad i = 1, \ldots, r$称为奇异值（singular values），$\boldsymbol{u}_i$ 称为左奇异向量（left-singular vectors），$\boldsymbol{v}_i$ 称为右奇异向量（right-singular vectors）。按照惯例，奇异值是有序的：$\sigma_1 \geqslant \sigma_2 \geqslant \cdots \geqslant \sigma_r \geqslant 0 .$

奇异值矩阵 $\boldsymbol{\Sigma}$ 是唯一的。需要注意 $\boldsymbol{\Sigma} \in \mathbb{R}^{m \times n}$ 是矩形的，且与 $\boldsymbol{A}$ 尺寸相同。这意味着 $\boldsymbol{\Sigma}$ 有一个包含奇异值的对角子矩阵，其他元素为零。备注：SVD 对任意 $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ 都成立。

旋转矩阵就是一个行列式为 $+1$ 的正交矩阵，也就是： $R^\top R = I, \quad \det(R) = 1$

SVD表示域和陪域（见线性代数中的像与核）的基变换。这与在同一向量空间中操作的特征值分解形成对比：后者在相同的向量空间中应用相同的基变化，然后撤消。奇异值分解的特殊之处在于这两个不同的基同时被奇异值矩阵$\boldsymbol{\Sigma}$ 连接起来。

标准正交基(ONB)

左奇异向量和右奇异向量的直观理解，详见《SVD 中的左奇异向量和右奇异向量.md》

特征值分解 vs. 奇异值分解

考虑特征值分解 \[ \boldsymbol{A} = \boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{-1} \] 和奇异值分解 \[ \boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{-1}, \] 下面回顾一下它们的核心内容：

对于任意矩阵 $\mathbb{R}^{m \times n}$，奇异值分解总是存在的。而特征值分解仅对平方矩阵 $\mathbb{R}^{n \times n}$ 有效，并且仅当我们能找到 $\mathbb{R}^n$ 的特征向量的基时才存在。
特征值分解矩阵 $\boldsymbol{P}$ 中的向量不一定是正交的，即基的变化不是简单的旋转和缩放。而另一方面，奇异值分解中矩阵 $\boldsymbol{U}$ 和 $\boldsymbol{V}$ 中的向量是正交的，因此它们确实表示旋转。
特征值分解和奇异值分解都是三个线性映射的组合：
- 定义域的基变换；
- 每个新基向量的缩放都是独立的，并从定义域映射到陪域；
- 陪域的基变换。特征值分解和奇异值分解的一个关键区别是，在奇异值分解中，定义域和陪域可以是不同维数的向量空间。
在奇异值分解中，左奇异向量矩阵 $\boldsymbol{U}$ 和右奇异向量矩阵 $\boldsymbol{V}$ 通常不是互逆的（它们在不同的向量空间中执行基变换）。在特征值分解中，基变化矩阵 $\boldsymbol{U}$ 和 $\boldsymbol{U}^{-1}$ 是互逆的。
在奇异值分解中，对角矩阵 $\boldsymbol{\Sigma}$ 中的项都是实的、非负的，这对于特征值分解中的对角矩阵则不一定成立。
奇异值分解和特征值分解通过它们的投影关系密切相关：
- $\boldsymbol{A}$ 的左奇异向量是 $\boldsymbol{A} \boldsymbol{A}^\top$ 的特征向量；
- $\boldsymbol{A}$ 的右奇异向量是 $\boldsymbol{A}^\top \boldsymbol{A}$ 的特征向量；
- $\boldsymbol{A}$ 的非零奇异值是 $\boldsymbol{A} \boldsymbol{A}^\top$ 和 $\boldsymbol{A}^\top \boldsymbol{A}$ 的非零特征值的平方根。
对于对称矩阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$，特征值分解和奇异值分解是相同的，这符合谱定理（定理 4.15）。

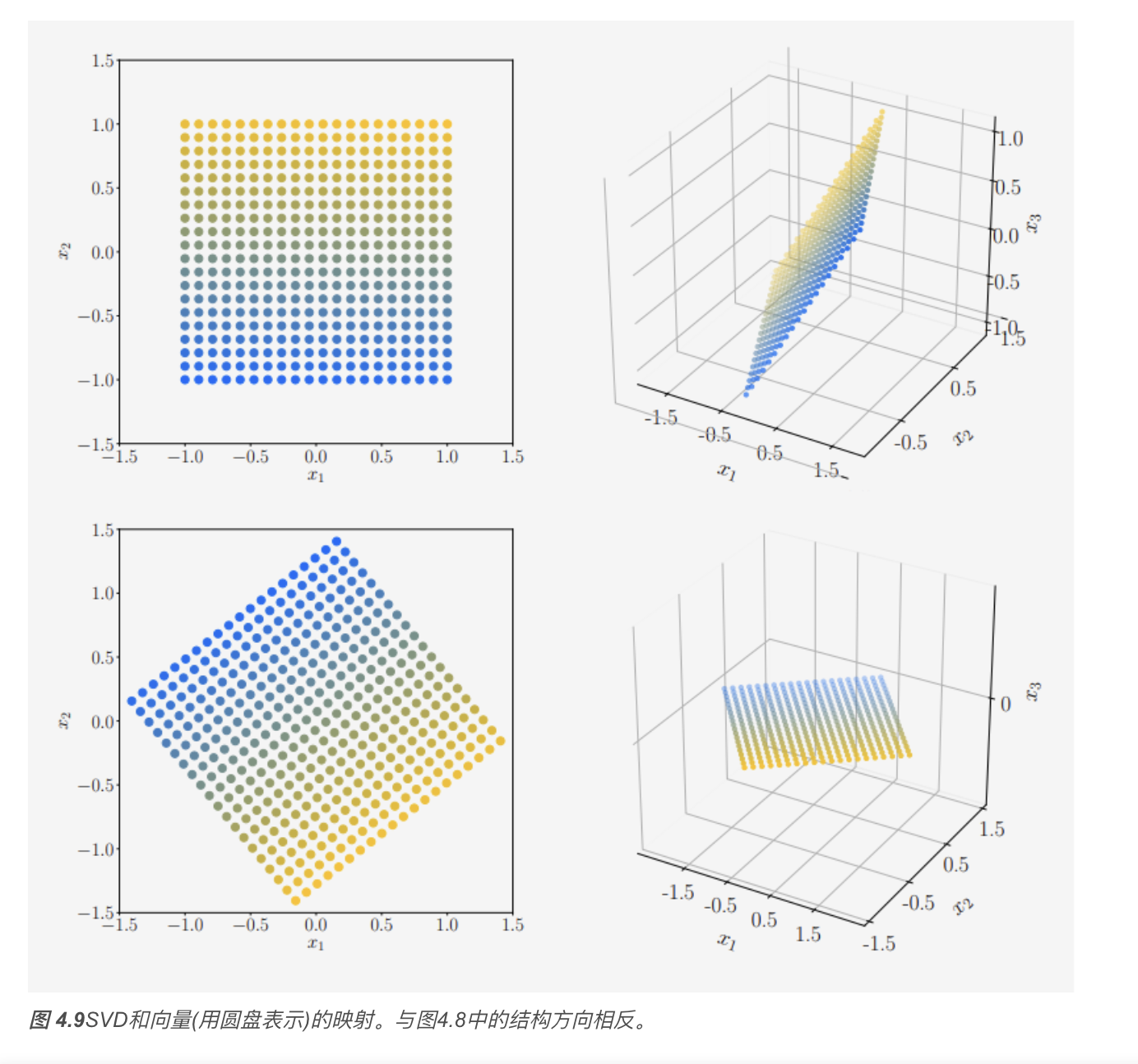
图解SVD_2

矩阵逼近

我们可以使用奇异值分解（SVD）将秩$r$ 矩阵$\boldsymbol{A}$降为秩$k$矩阵$ $ ，这是一种取主要成分并达到最优的（在谱范数意义上）方式。我们可以将秩$k$矩阵对$ $的逼近解释为有损压缩的一种方法。因此，矩阵的低秩逼近出现在许多机器学习应用中，例如图像处理、噪声滤波和不适定问题的正则化。此外，它在降维和主成分分析中起着关键作用

秩为 $r$ 的矩阵 $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ 能被写成秩 $1$ 矩阵 $\boldsymbol{A}_i$ 的和： \[ \boldsymbol{A} = \sum_{i=1}^{r} \sigma_{i} \boldsymbol{u}_{i} \boldsymbol{v}_{i}^{\top} = \sum_{i=1}^{r} \sigma_{i} \boldsymbol{A}_{i}, \] 其中，外积矩阵 $\boldsymbol{A}_{i}$ 的权重为第 $i$ 个奇异值 $\sigma_{i}$。

矩阵分类关系图

Matrix Phylogeny

可对角化其实就是可特征值分解。

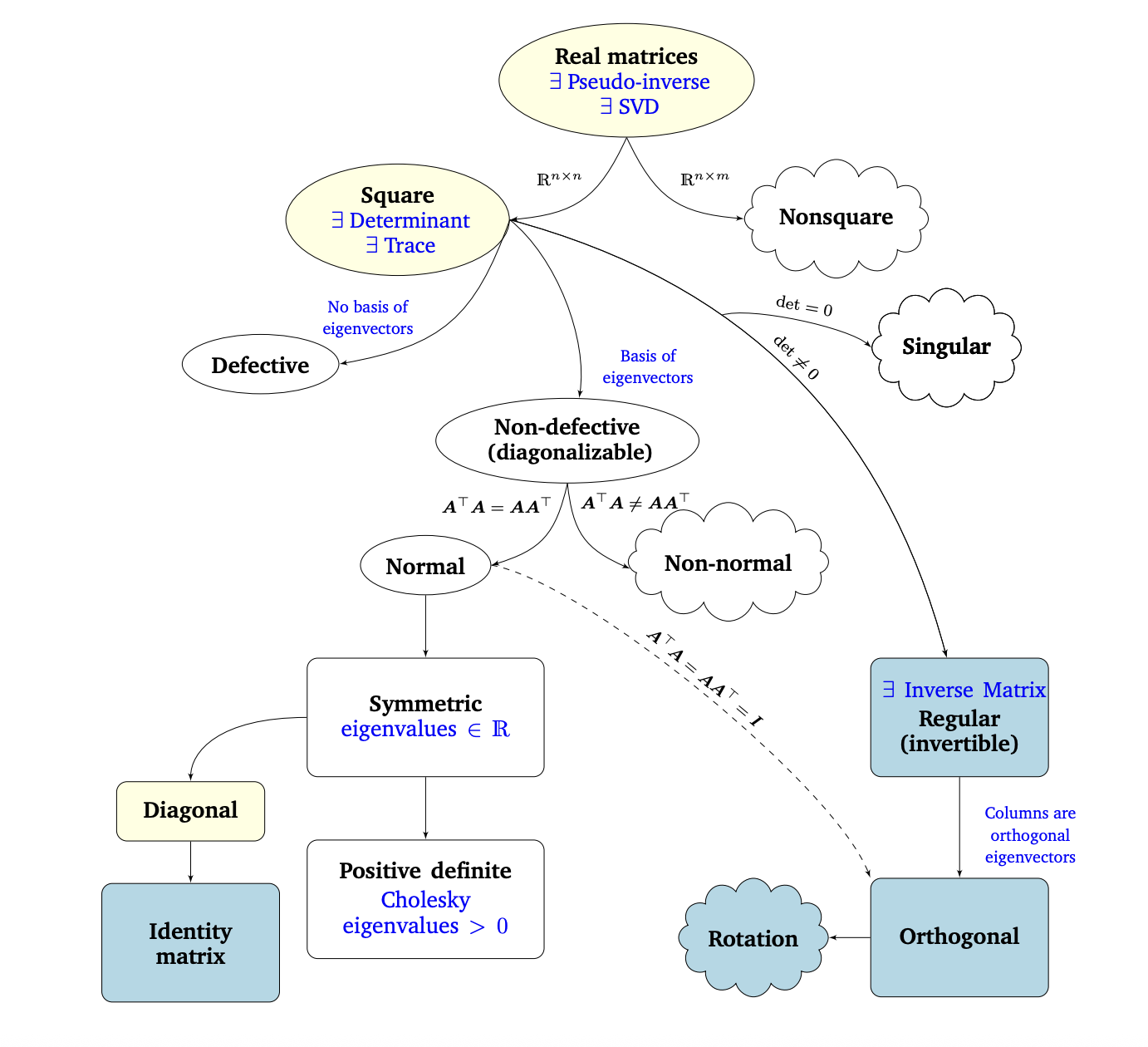
矩阵分类关系图

在第2章和第3章中，我们介绍了线性代数和解析几何的基础知识。在这一章中，我们研究了矩阵和线性映射的基本特征。图4.13描述了不同类型矩阵之间关系的 Phylogeny（黑色箭头表示子集）以及我们可以对其执行的操作（蓝色）。

我们考虑所有实矩阵（real matrices）$\boldsymbol{A} \in \mathbb{R}^{n \times m}$。对于非方阵（其中 $n \neq m$），奇异值分解总是存在的，正如我们在本章中看到的。以方阵（square matrices）$\boldsymbol{A} \in \mathbb{R}^{n \times n}$ 为中心，行列式告诉我们方阵是否具有逆矩阵（inverse matrix），即它是否属于正则可逆矩阵类。如果 $n \times n$ 矩阵具有 $n$ 个线性无关的特征向量，则矩阵是非退化的（non-defective），并且存在特征值分解（定理4.12）。我们知道，重复的特征值可能导致矩阵退化，这种矩阵是不能对角化的。

No basis of eigenvectors 特征向量不是基； Basis of eigenvectors 特征向量是基。 Singular 奇异的 Orthogonal 正交的

非奇异矩阵和非退化矩阵是不同的。例如，旋转矩阵是可逆的（行列式是非零的），但不一定可对角化（特征值不能保证是实数）。

以上这句话的例子详见《非奇异矩阵和非退化矩阵.md》

我们进一步研究了非退化 $n \times n$ 方阵的分支。如果条件$\boldsymbol{A}^{\top} \boldsymbol{A} = \boldsymbol{A} \boldsymbol{A}^{\top}$成立，则 $\boldsymbol{A}$ 是正规的（normal）。此外，如果更严格的条件$\boldsymbol{A}^{\top} \boldsymbol{A} = \boldsymbol{A} \boldsymbol{A}^{\top} = \boldsymbol{I}$成立，则 $\boldsymbol{A}$ 称为正交（orthogonal，见定义3.8）。正交矩阵集是正则（可逆）矩阵的子集，满足$\boldsymbol{A}^{\top} = \boldsymbol{A}^{-1}.$

正规矩阵有一个常见的子集，即对称矩阵 $\boldsymbol{S} \in \mathbb{R}^{n \times n}$，它满足$\boldsymbol{S} = \boldsymbol{S}^{\top}.$对称矩阵只有实特征值。对称矩阵的子集由正定矩阵 $\boldsymbol{P}$ 组成，正定矩阵 $\boldsymbol{P}$ 对所有 $\boldsymbol{x} \in \mathbb{R}^{n} \backslash \{\mathbf{0}\}$ 满足条件$\boldsymbol{x}^{\top} \boldsymbol{P} \boldsymbol{x} > 0.$在这种情况下，存在唯一的 Cholesky 分解（Cholesky decomposition，定理4.18）。正定矩阵只有正特征值且总是可逆的（即，具有非零行列式）。

对称矩阵的另一个子集由对角矩阵（diagonal matrices）$\boldsymbol{D}$ 组成。对角矩阵在乘法和加法下是闭合的，但不一定形成一个群（只有当所有的对角项都不为零时才是这种情况，这样矩阵才是可逆的）。一种特殊的对角矩阵是单位矩阵 $\boldsymbol{I}$。

Identity matrix 单位矩阵

上表来源鸢尾花那本书Book4_ch24 《矩阵力量》

向量微积分

Vector Calculus

$f$导数的方向指向$f$最陡峭的上升方向。

组合符号 $C_n^m$ 也可写成 $\binom{n}{m}$。

泰勒级数

泰勒级数是函数$ f$的无穷项和的表示。这些项是用$ f$的导数来确定的。多项式逼近函数的泰勒级数。

泰勒级数

对于一个平滑的函数 $ f ^{}, f: $ （$ f ^{} $ 表示 $ f $ 连续且可微无穷多次）， $ f $ 在 $ x_0 $ 的泰勒级数Taylor series）定义为：
\[ T_{\infty}(x) = \sum_{k=0}^{\infty} \frac{f^{(k)}\left(x_{0}\right)}{k !} \left(x - x_{0}\right)^{k} \]

当 $ x_0 = 0 $ 时，我们得到麦克劳林级数（Maclaurin series），它是泰勒级数的特殊实例。如果 $ f(x) = T_{}(x) $，那么 $ f $ 称为解析的（analytic）。

备注：一般来说，$ n $ 次泰勒多项式是非多项式函数的近似值。它在 $ x_0 $ 附近与 $ f $ 相似。然而，$ n $ 次泰勒多项式用 $ k n $ 次多项式表示 $ f $ 已经足够精确了，因为导数 $ f^{(i)}, i > k $ 可能为 $ 0 $。

泰勒级数中的 $x_0$（也叫展开点）原则上可以选任意实数或复数，不过能不能用它准确表示函数，还得看收敛性和函数的可导性条件。

备注：
泰勒级数是幂级数的特例，幂级数表达式为：
\[ f(x) = \sum_{k=0}^{\infty} a_{k} (x - c)^{k} \] 其中 $a_k$为系数，$c$为常数。定义5.4中的式子是它的特殊形式。

微分法则

下面，我们用 $ f' $ 表示 $ f $ 的导数，简要地说明基本的微分规则：

乘积法则：

\[ (f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \]

除法法则：

\[ \left(\frac{f(x)}{g(x)}\right)' = \frac{f'(x) g(x) - f(x) g'(x)}{\left(g(x)\right)^{2}} \]

加法法则：

\[ (f(x) + g(x))' = f'(x) + g'(x) \]

链式法则：

\[ (g(f(x)))' = (g \circ f)'(x) = g'(f(x)) \cdot f'(x) \]

这里，$ g f $ 表示函数复合：
\[ x \mapsto f(x) \mapsto g(f(x)) \]

偏微分与梯度

导数对多变量函数的推广是梯度(gradient)。

我们通过一次改变一个变量并保持其他变量不变来求函数$ f$相对于$ x$的偏导数。梯度就是这些偏导数(partial derivatives)构成的的集合。

将它们组成一个行向量： \[ \nabla_{\boldsymbol{x}} f = \operatorname{grad} f = \frac{\mathrm{d} f}{\mathrm{d} \boldsymbol{x}} = \left[ \frac{\partial f(\boldsymbol{x})}{\partial x_{1}},\ \frac{\partial f(\boldsymbol{x})}{\partial x_{2}},\ \cdots,\ \frac{\partial f(\boldsymbol{x})}{\partial x_{n}} \right] \in \mathbb{R}^{1 \times n} \qquad (5.40) \]

其中 $ n $ 是变量个数，$ 1 $ 是 $ f $ 的像/值域/陪域的维数。这里，我们定义了列向量$\boldsymbol{x} = \left[ x_{1}, \ldots, x_{n} \right]^{\top} \in \mathbb{R}^n.$ 式 (5.40) 中的行向量称为 $ f $ 的梯度(gradient) 或雅可比矩阵(Jacobian)，是第 5.1 节中导数的推广。

备注（梯度用行向量表示）：

向量通常用列向量表示，将梯度向量定义为列向量在文献中并不少见。我们将梯度向量定义为行向量的原因有两个：首先，我们可以一致地将梯度推广到向量值函数$f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$（然后梯度变成矩阵）。其次，我们可以很方便地应用多变量链式法则，而不必注意梯度的维数。

链式法则

考虑两个变量 $x_{1}$, $x_{2}$ 的函数$f: \mathbb{R}^{2} \rightarrow \mathbb{R}.$此外，$x_{1}(t)$ 和 $x_{2}(t)$ 本身就是 $t$ 的函数。为了计算 $f$ 相对于 $t$ 的导数，我们需要对多元函数使用链式法则： \[ \frac{\mathrm{d} f}{\mathrm{d} t} = \begin{bmatrix} \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}} \end{bmatrix} \begin{bmatrix} \frac{\partial x_{1}(t)}{\partial t} \\ \frac{\partial x_{2}(t)}{\partial t} \end{bmatrix} = \frac{\partial f}{\partial x_{1}} \frac{\partial x_{1}}{\partial t} + \frac{\partial f}{\partial x_{2}} \frac{\partial x_{2}}{\partial t}. \] 其中 $\mathrm{d}$ 表示全导数，$\partial$ 表示偏导数。

多变量链式法则

如果 $f(x_{1}, x_{2})$ 是 $x_{1}$ 和 $x_{2}$ 的函数，其中 $x_{1}(s, t)$ 和 $x_{2}(s, t)$ 是两个变量 $s$ 和 $t$ 的函数，则用链式法则可得偏导数： \[ \frac{\partial f}{\partial s} = \frac{\partial f}{\partial x_{1}} \frac{\partial x_{1}}{\partial s} + \frac{\partial f}{\partial x_{2}} \frac{\partial x_{2}}{\partial s}, \]

\[ \frac{\partial f}{\partial t} = \frac{\partial f}{\partial x_{1}} \frac{\partial x_{1}}{\partial t} + \frac{\partial f}{\partial x_{2}} \frac{\partial x_{2}}{\partial t}. \]

将梯度写成矩阵乘法的形式为： \[ \frac{\mathrm{d} f}{\mathrm{d}(s, t)} = \frac{\partial f}{\partial \boldsymbol{x}} \frac{\partial \boldsymbol{x}}{\partial (s, t)} = \underbrace{ \begin{bmatrix} \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}} \end{bmatrix} }_{\frac{\partial f}{\partial \boldsymbol{x}}} \underbrace{ \begin{bmatrix} \frac{\partial x_{1}}{\partial s} & \frac{\partial x_{1}}{\partial t} \\ \frac{\partial x_{2}}{\partial s} & \frac{\partial x_{2}}{\partial t} \end{bmatrix} }_{\frac{\partial \boldsymbol{x}}{\partial (s, t)}}. \]

这种将链式法则写成矩阵乘法的简洁方法，只有在将梯度定义为行向量时才直接成立。否则，需要对矩阵进行转置以匹配维数。当对象是向量或矩阵时，转置很简单；但当对象是张量时（将在后面讨论），转置就不再是小事了。

向量值函数的梯度

雅可比矩阵

向量值函数的所有一阶偏导数的集合称为雅可比矩阵（Jacobian）。雅可比矩阵 $\mathbf{J}$ 是一个 $m \times n$ 矩阵，我们将其定义如下： \[ \mathbf{J} = \nabla_{\mathbf{x}} \mathbf{f} = \frac{\mathrm{d} \mathbf{f}(\mathbf{x})}{\mathrm{d} \mathbf{x}} = \left[ \frac{\partial \mathbf{f}(\mathbf{x})}{\partial x_{1}} \quad \cdots \quad \frac{\partial \mathbf{f}(\mathbf{x})}{\partial x_{n}} \right]. \]

具体写成矩阵形式为： \[ \begin{equation} \mathbf{J} = \begin{bmatrix} \dfrac{\partial f_{1}(\mathbf{x})}{\partial x_{1}} & \cdots & \dfrac{\partial f_{1}(\mathbf{x})}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \dfrac{\partial f_{m}(\mathbf{x})}{\partial x_{1}} & \cdots & \dfrac{\partial f_{m}(\mathbf{x})}{\partial x_{n}} \end{bmatrix}, \tag{5.58} \end{equation} \] 其中 \[ \mathbf{x} = \begin{bmatrix} x_{1} \\ \vdots \\ x_{n} \end{bmatrix}, \quad J(i,j) = \frac{\partial f_{i}}{\partial x_{j}}. \]

雅可比矩阵表示我们想要的坐标变换。如果坐标变换是线性的（如我们的例子），那么它是精确的，（5.66）精确地恢复了（5.62）中的基变化矩阵。如果坐标变换是非线性的，雅可比矩阵则用一个线性变换局部地逼近这个非线性变换。雅可比行列式 $|\operatorname{det}(\boldsymbol{J})|$ 的绝对值是变换坐标时面积或体积的缩放因子。

方法一、

为了开始使用线性代数的方法，我们首先确定 $\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}$ 和 $\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}$ 都是 $\mathbb{R}^2$ 的基。我们要有效地执行的是从 $\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}$ 到 $\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}$ 的基变换，就得寻找实现基变换的变换矩阵。利用第2.7.2节的结果，我们确定了所需的基变换矩阵为： \[ \boldsymbol{J} = \begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix} \tag{5.62} \]

它使得 $\boldsymbol{J}\boldsymbol{b}_{1} = \boldsymbol{c}_{1}, \quad \boldsymbol{J}\boldsymbol{b}_{2} = \boldsymbol{c}_{2}$。矩阵 $\boldsymbol{J}$ 的行列式的绝对值为： \[ \left|\det(\boldsymbol{J})\right| = 3, \] 这正是我们在寻找的缩放因子。也就是说， $(\boldsymbol{c}_{1}, \boldsymbol{c}_{2})$ 所张成的平行四边形的面积是 $(\boldsymbol{b}_{1}, \boldsymbol{b}_{2})$ 所张成面积的三倍。

把 $\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}$ 坐标变换成 $\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\}$ 的坐标，是左乘$\boldsymbol{J}^{-1}$；反向是左乘$\boldsymbol{J}$。

方法二、

线性代数方法适用于线性变换；对于非线性变换（与第6.7节有关），我们有基于偏微分的更一般的方法。

在这种方法中，我们考虑执行变量变换的函数$\boldsymbol{f}: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}.$在我们的例子中，$\boldsymbol{f}$ 将关于 $(\boldsymbol{b}_{1}, \boldsymbol{b}_{2})$ 的任意向量 $\boldsymbol{x} \in \mathbb{R}^{2}$ 的坐标映射到关于 $(\boldsymbol{c}_{1}, \boldsymbol{c}_{2})$ 的坐标 $\boldsymbol{y} \in \mathbb{R}^{2}$。我们想确定这个映射，这样就可以计算出一个面积（或体积）在 $\boldsymbol{f}$ 变换下是如何变化的。为此，我们需要找出 $\boldsymbol{f}(\boldsymbol{x})$ 在 $\boldsymbol{x}$ 微小变化时的变化方式。雅可比矩阵 \[ \frac{\mathrm{d} \boldsymbol{f}}{\mathrm{d} \boldsymbol{x}} \in \mathbb{R}^{2 \times 2} \] 正是这个问题的答案。由下式定义的映射： \[ y_{1} = -2x_{1} + x_{2}, \qquad y_{2} = x_{1} + x_{2}, \] 我们得到了 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 之间的函数关系。这允许我们计算偏导数： \[ \frac{\partial y_{1}}{\partial x_{1}}=-2, \quad \frac{\partial y_{1}}{\partial x_{2}}=1, \quad \frac{\partial y_{2}}{\partial x_{1}}=1, \quad \frac{\partial y_{2}}{\partial x_{2}}=1. \]

将它们组合成雅可比矩阵： \[ \boldsymbol{J} = \begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} \\ \frac{\partial y_{2}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{2}} \end{bmatrix} = \begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix} \tag{5.66} \]

雅可比矩阵表示我们想要的坐标变换。如果坐标变换是线性的（如我们的例子），那么它是精确的，（5.66）正好恢复了（5.62）中的基变化矩阵。 如果坐标变换是非线性的，雅可比矩阵则用一个线性变换局部地逼近这个非线性变换。雅可比行列式的绝对值 \[ \left|\det(\boldsymbol{J})\right| = 3 \] 就是变换坐标时面积或体积的缩放因子。在我们的例子中，结果正好是 3。

向量值函数的梯度

给定： \[ \mathbf{f}(\mathbf{x}) = \mathbf{A} \mathbf{x} \] 其中：

$\mathbf{f}(\mathbf{x}) \in \mathbb{R}^M$（输出是 $M$ 维向量）
$\mathbf{A} \in \mathbb{R}^{M \times N}$
$\mathbf{x} \in \mathbb{R}^N$

这是一个线性映射：$\mathbf{x} \mapsto \mathbf{A} \mathbf{x}$。

向量值函数的梯度是 $A$。

反向传播与自动微分法

在许多机器学习应用中，我们通过执行梯度下降（第7.1节）来找到好的模型参数，这基于我们可以计算目标函数相对于模型参数的梯度。对于给定的目标函数，我们可以通过微积分和应用链式法则来获得关于模型参数的梯度；见第5.2.2节。在第5.3节中，我们已经研究了线性回归模型的平方损失函数的梯度。

反向传播是数值分析中称为自动微分(automatic differentiation)技术的一个特例。我们可以把自动微分看作是一套技术，它通过处理中间变量和应用链式法则，在数值上（而不是符号化地）计算函数的精确（达到机器精度）梯度。自动微分应用了一系列基本算术运算，例如加法和乘法，以及基本函数，例如：$⁡ \sin , \cos , \exp , \log$将链式法则应用到这些运算中，可以自动计算相当复杂函数的梯度。自动微分适用于一般的计算机程序，有正向和反向两种模式。

直观地说，正向和反向模式在乘法的顺序上是不同的。由于矩阵乘法的结合性，我们有以下两种选择： \[ \begin{equation} \frac{\mathrm{d} y}{\mathrm{d} x} = \left( \frac{\mathrm{d} y}{\mathrm{d} b} \frac{\mathrm{d} b}{\mathrm{d} a} \right) \frac{\mathrm{d} a}{\mathrm{d} x} \qquad (5.120) \end{equation} \]

\[ \begin{equation} \frac{\mathrm{d} y}{\mathrm{d} x} = \frac{\mathrm{d} y}{\mathrm{d} b} \left( \frac{\mathrm{d} b}{\mathrm{d} a} \frac{\mathrm{d} a}{\mathrm{d} x} \right) \qquad (5.121) \end{equation} \]

方程（5.120）是反向模式（reverse mode），因为梯度通过数据流向后传播。方程（5.121）是正向模式（forward mode），其中梯度随数据从左到右流过整个图。

下面，我们将重点介绍反向模式的自动微分，即反向传播。在神经网络中，输入的维数通常比标签的维数高得多，所以反向模式比正向模式计算量要少得多。

具体的例子详见《损失函数的梯度计算例子.md》

概率与分布

Probability and Distributions

概率论可以看作是布尔逻辑的推广。在机器学习的背景下，它经常以这种方式应用于自动推理系统的形式化设计。

在机器学习和统计学中，有两种主要的概率解释：贝叶斯主义和频率主义(Bishop, 2006;Efron and Hastie, 2016)。贝叶斯主义使用概率来指定用户对事件的不确定性程度。它有时被称为“主观概率”或“置信程度”。频率主义则考虑感兴趣的事件与所发生事件的总数的相对频率。一个事件的概率定义为当发生事件的总数趋于无限时，该事件的相对频率。

许多机器学习的概率模型描述使用惰性符号和术语，这会令人困惑的。这篇文章也不例外。有多个不同的概念都被称为“概率分布”，读者往往要从上下文中获知其中的含义。一个有助于理解概率分布的技巧是检查我们是在尝试建立一个分类的（离散的随机变量）模型还是一个连续的（连续的随机变量）模型。我们在机器学习中处理的问题的种类与我们要考虑分类模型还是连续模型密切相关。

在抽第二枚硬币之前放回了第一枚抽到的硬币，这意味着两次抽硬币是相互独立的。

概率空间 $(\Omega, \mathcal{A}, P)$，

示例：连续两次抛硬币

样本空间 \[ \Omega = \{hh, ht, th, tt\} \] 这里每个元素（样本点）表示两次抛硬币的具体结果。例如 $hh$ = 第一次正面、第二次正面。
事件空间 事件就是样本空间的子集。比如：
- 事件 $A=\{\text{hh}\}$：两次都是正面。
- 事件 $B=\{\text{ht},\text{th}\}$：恰好出现一次正面。
- 事件 $C=\{\text{hh},\text{ht},\text{th}\}$：至少出现一次正面。
所有可能的事件集合（即事件空间 $\mathcal{A}$）在离散情况下就是 $\Omega$ 的幂集： \[ \mathcal{A} = \{ \emptyset, \{hh\}, \{ht\}, \{th\}, \{tt\}, \{hh,ht\}, \dots, \Omega \}. \]
概率分布 假设硬币均匀独立，样本空间中每个结果的概率都是 $1/4$。那么：
- $P(A)=P(\{hh\})=1/4$。
- $P(B)=P(\{ht,th\})=1/4+1/4=1/2$。
- $P(C)=P(\{hh,ht,th\})=3/4$。

总结

样本空间 $\Omega$：所有可能的基本结果。
事件空间 $\mathcal{A}$：由样本空间的子集组成，每个子集就是一个“事件”。
概率 $P$：为每个事件赋予一个数，满足概率公理。

给定一个概率空间 $(\Omega, \mathcal{A}, P)$，我们希望使用它来模拟一些现实世界的现象。在机器学习中，我们经常避免直接引用概率空间，而是引用感兴趣的量上的概率，我们用 $\mathcal{T}$ 表示。在这本书中，我们把 $\mathcal{T}$ 称为目标空间（target space），把 $\mathcal{T}$ 的元素称为状态。我们引入了一个函数 $X : \Omega \to \mathcal{T}$它接受 $\Omega$ 元素（一个结果，样本点），并返回感兴趣对象 $x$ 在 $\mathcal{T}$ 中的特定量（值）。从 $\Omega$ 到 $\mathcal{T}$ 的这种关联/映射称为随机变量（random variable）。

例如，考虑投掷两枚硬币并计算正面数。随机变量 $X$ 映射到三种可能的结果：$X(hh) = 2, \quad X(ht) = 1, \quad X(th) = 1, \quad X(tt) = 0$在这个特殊的情况下，$\mathcal{T} = \{0,1,2\}$，我们感兴趣的是 $\mathcal{T}$ 中元素的概率。对于有限的样本空间 $\Omega$ 和有限的 $\mathcal{T}$，随机变量对应的函数本质上是一个查找表。对于任意子集 $S \subseteq \mathcal{T}$，我们将$P_X(S) \in [0,1]$（概率）与随机变量 $X$ 对应的特定事件联系起来。例 6.1 提供了具体说明。

将 $X $<u>*输出的概率*</u>和$$中样本的概率这两个不同的概念等同起来!

Example 6.1

This toy example is essentially a biased coin flip example. We assume that the reader is already familiar with computing probabilities of intersections and unions of sets of events. A gentler introduction to probability with many examples can be found in chapter 2 of Walpole et al. (2011).

Consider a statistical experiment where we model a funfair game consisting of drawing two coins from a bag (with replacement). There are coins from USA (denoted as $) and UK (denoted as £) in the bag, and since we draw two coins from the bag, there are four outcomes in total. The state space or sample space $\Omega$ of this experiment is then \[ (\$, \$), (\$, £), (£, \$), (£, £). \] Let us assume that the composition of the bag of coins is such that a draw returns at random a $ with probability 0.3.

The event we are interested in is the total number of times the repeated draw returns $. Let us define a random variable $X$ that maps the sample space $\Omega$ to $\mathcal{T}$, which denotes the number of times we draw $ out of the bag. We can see from the preceding sample space we can get zero $, one $, or two $s, and therefore $\mathcal{T} = \{0, 1, 2\}$. The random variable $X$ (a function or lookup table) can be represented as a table like the following: \[ \begin{align} X((\$, \$)) &= 2 \tag{6.1}\\ X((\$, £)) &= 1 \tag{6.2}\\ X((£, \$)) &= 1 \tag{6.3}\\ X((£, £)) &= 0. \tag{6.4} \end{align} \] Since we return the first coin we draw before drawing the second, this implies that the two draws are independent of each other, which we will discuss in Section 6.4.5. Note that there are two experimental outcomes which map to the same event, where only one of the draws returns $. Therefore, the probability mass function (Section 6.2.1) of $X$ is given by \[ \begin{align} P(X=2) &= P((\$, \$)) \nonumber \\ &= P(\$) \cdot P(\$) \nonumber \\ &= 0.3 \cdot 0.3 = 0.09 \tag{6.5}\\ P(X=1) &= P((\$, £) \cup (\,£, \$)) \nonumber \\ &= P((\$, £)) + P((\,£, \$)) \nonumber \\ &= 0.3 \cdot (1 - 0.3) + (1 - 0.3) \cdot 0.3 = 0.42 \tag{6.6}\\ P(X=0) &= P((\,£, £)) \nonumber \\ &= P(£) \cdot P(£) \nonumber \\ &= (1 - 0.3) \cdot (1 - 0.3) = 0.49. \tag{6.7} \end{align} \]

离散状态数值化特别有用，因为我们经常需要考虑随机变量的期望值

不幸的是，机器学习许多相关文献使用的符号和术语隐藏了样本空间 $\Omega$、目标空间 $\mathcal{T}$ 和随机变量 $X$ 之间的区别。对于随机变量 $X$ 的一组可能结果的值 $x$，即 $x \in \mathcal{T}$，$p(x)$ 表示随机变量 $X$ 取结果 $x$ 的概率。对于离散随机变量，这表示为 $p(X = x)$，这称为概率质量函数（probability mass function）。概率质量函数通常被称为“分布”。

对于连续变量，$p(x)$ 称为概率密度函数（probability density function，通常称为密度），而累积分布函数 $P(x \le X)$ 通常也被称为“分布”。在本章中，我们将使用符号 $X$ 来表示一元和多元随机变量，并分别用 $x$ 和 $\boldsymbol{x}$ 表示状态。

我们用“概率分布”表达离散的概率质量函数以及连续的概率密度函数，尽管这在技术上是不正确的。与大多数机器学习文献一样，我们也依赖上下文来区分“概率分布”这个短语的不同用法。

加法法则、乘法法则和贝叶斯定理

1、求和法则 \[ p(x) = \begin{cases} \sum_{y \in \mathcal{Y}} p(x,y), & \text{如果 $y$ 是离散的}, \\[1em] \int_{\mathcal{Y}} p(x,y)\,dy, & \text{如果 $y$ 是连续的}. \end{cases} \]

求和法则将联合分布与边缘分布联系了起来。

备注： 概率建模的许多计算困难都是由于应用了求和法则。当有许多变量或具有许多状态的离散变量时，求和法则执行的是高维求和或积分。执行高维求和或积分通常是难以计算，因为没有已知的多项式时间(polynomial-time)算法来精确计算它们。

2、乘法法则

乘法法则(product rule)，它将联合分布与条件分布联系起来： \[ \begin{equation} p(\boldsymbol{x}, \boldsymbol{y}) = p(\boldsymbol{y} \mid \boldsymbol{x}) \, p(\boldsymbol{x}) \qquad (6.22) \end{equation} \] 乘积法则可以解释为：两个随机变量的联合分布能被因子分解（乘积形式）为其他两个分布。这两个因子分别是：

第一个随机变量的边缘分布$p(\boldsymbol{x})$
给定第一个随机变量时，第二个随机变量的条件分布$p(\boldsymbol{y} \mid \boldsymbol{x})$

联合分布中随机变量的顺序是任意的，这意味着： \[ p(\boldsymbol{x}, \boldsymbol{y}) = p(\boldsymbol{x} \mid \boldsymbol{y}) \, p(\boldsymbol{y}) \] 准确地说，式（6.22）表示的是离散随机变量的概率质量函数。对于连续随机变量，乘积规则用概率密度函数（第 6.2.3 节）表示。

3、贝叶斯定理

在机器学习和贝叶斯统计中，如果我们观察到部分随机变量，我们通常会对未观察到的（潜在的）随机变量的推断感兴趣。假设我们有一些关于未观测随机变量 $\boldsymbol{x}$ 的先验（prior）知识 $p(\boldsymbol{x})$，并且我们可以观察到 $\boldsymbol{x}$ 和第二个随机变量 $\boldsymbol{y}$ 之间的关系 $p(\boldsymbol{y} \mid \boldsymbol{x})$。那么，如果我们观察到 $\boldsymbol{y}$，就可以利用贝叶斯定理，在给定 $\boldsymbol{y}$ 的观测值前提下，得出 $\boldsymbol{x}$ 的一些结论。

贝叶斯定理（也叫贝叶斯法则或贝叶斯定律）： \[ \begin{equation} \underbrace{p(\boldsymbol{x} \mid \boldsymbol{y})}_{\text{后验}} = \frac{\overbrace{p(\boldsymbol{y} \mid \boldsymbol{x})}^{\text{似然}} \; \overbrace{p(\boldsymbol{x})}^{\text{先验}}}{\underbrace{p(\boldsymbol{y})}_{\text{证据}}} \qquad (6.23) \end{equation} \] 似然（likelihood，有时也被称为“测量模型”）$p(\boldsymbol{y} \mid \boldsymbol{x})$描述了$\boldsymbol{x}$和$\boldsymbol{y}$是如何相关的。对于离散概率分布，它是在已知潜在变量$\boldsymbol{x}$前提下，数据$\boldsymbol{y}$的概率。注意，似然$p(\boldsymbol{y} \mid \boldsymbol{x})$不是$\boldsymbol{x}$的分布，而是$\boldsymbol{y}$的分布(个人注：但是关于$x$的函数，见下面的场景)。并且我们称$p(\boldsymbol{y} \mid \boldsymbol{x})$为“$\boldsymbol{x}$的似然（给定$\boldsymbol{y}$）”或“给定$\boldsymbol{x}$，$\boldsymbol{y}$的概率”，但不是$\boldsymbol{y}$的似然（MacKay, 2003）。

1、场景：连续测量——身高推断

假设我们想根据某人的身高 $Y$ 推断其年龄 $X$（以年为单位）。

先验分布 $p(x)$：假设我们认为年龄 $X$ 在 0–100 岁之间大致服从均匀分布： \[ p(x) = \frac{1}{100}, \quad 0 \le x \le 100 \]

似然函数 $p(y \mid x)$：假设对于给定年龄 $X=x$，身高 $Y$ 服从正态分布： \[ Y \mid X=x \sim \mathcal{N}(\mu=x\cdot0.5 + 50, \sigma^2=10^2) \] 即 $\mu = 0.5x + 50$ 厘米，$\sigma = 10$ 厘米。

观测值：假设测得身高 $Y = 80$ 厘米，我们想推断年龄 $X$。

2、连续贝叶斯公式

连续情况下的贝叶斯定理为： \[ p(x \mid y) = \frac{p(y \mid x)\, p(x)}{p(y)}, \quad \text{其中 } p(y) = \int_0^{100} p(y \mid x)\, p(x)\, dx \]

分子：似然 × 先验

分母：归一化因子（确保后验密度积分为1）

所以： \[ p(x \mid Y=80) = \frac{\frac{1}{\sqrt{2\pi}10} \exp\Big[-\frac{(80-(0.5x+50))^2}{2\cdot10^2}\Big] \cdot \frac{1}{100}}{\int_0^{100} \frac{1}{\sqrt{2\pi}10} \exp\Big[-\frac{(80-(0.5x+50))^2}{2\cdot10^2}\Big] \cdot \frac{1}{100} dx} \]

$p(y x) = $

表示根据$y$的分布函数，在$y=80$对应的关于$x$的函数。也就是，针对不同的$x$, $y=80$ 的概率。

3、直观理解

先验 $p(x)$：在观测身高之前我们对年龄的猜测。

似然 $p(y\mid x)$：身高为 80 厘米时，不同年龄产生这个观测的可能性。

后验 $p(x\mid y)$：结合观测数据后的年龄分布。

\[ p(y) := \int p(y \mid x) p(x) \, dx = \mathbb{E}_{X}[p(y \mid x)] \tag{6.27} \] 是边缘似然 / 证据（marginal likelihood / evidence）。

(6.27) 的右边使用我们在第 6.4.1 节中定义的期望操作符。根据定义，边缘似然是 (6.23) 贝叶斯公式的分子对潜在变量 $ $ 的积分。因此，边缘似然与 $ $ 无关，它保证了后验 $ p( ) $ 被标准化。边缘似然也可以解释为期望似然，关于先验 $ p() $ 的期望。除了用于后验标准化之外，边缘似然在贝叶斯模型选择中也起着重要作用，我们将在第 8.6 节中讨论。由于 (8.44) 中的积分，证据（evidence）通常很难计算。

贝叶斯定理 (6.23) 允许我们反转由似然给出的 $ $ 和 $ $ 之间的关系。因此，贝叶斯定理有时也被称为概率逆（probabilistic inverse）。

备注： 在贝叶斯统计中，后验分布是我们感兴趣的量，因为它包含了所有来自先验和数据的可用信息。我们把重点放在后验的一些统计量上，例如后验的最大值，这将在8.3节中讨论。然而，只关注后验的统计量会导致信息的丢失。如果我们在更大的背景下思考，那么后验还可以在决策系统中使用。拥有完整的后验非常有用，它可以得到对干扰具有鲁棒性的决策。例如，在基于模型的强化学习中，Deisenroth等人(2015)表明，使用似然转移函数的完全后验分布可以非常快速(数据/样本高效)学习，而关注最大的后验则会导致一致性失败。因此，拥有完整的后验对于下游任务非常有用。在第9章中，我们将在线性回归的背景下继续这个讨论。

期望值

期望值的概念是机器学习的中心，概率本身的一些基本概念可以从期望值派生 (Whittle, 2000)。

定义 6.3 期望值

关于单变量连续随机变量 $X \sim p(X)$ 的函数
$g : \mathbb{R} \to \mathbb{R}$ 的期望值（expected value）为： \[ \mathbb{E}_{X}[g(x)] = \int_{\mathcal{X}} g(x) \, p(x) \, \mathrm{d}x \] 相应地，关于离散随机变量 $X \sim p(X)$ 的函数 $g$ 的期望值为： \[ \mathbb{E}_{X}[g(x)] = \sum_{x \in \mathcal{X}} g(x) \, p(x) \] 其中 $\mathcal{X}$ 是随机变量 $X$ 的可能结果的集合（目标空间）。

在本节中，我们考虑离散随机变量的数值结果。通过观察函数 $g$ 以实数作为输入可以看出这一点。

定义 6.4 均值:

状态 $\boldsymbol{x} \in \mathbb{R}^D$ 的随机变量 $X$ 的均值（mean）为平均值（average），定义为
\[ \mathbb{E}_{X}[\boldsymbol{x}] = \begin{bmatrix} \mathbb{E}_{X_1}[x_1] \\ \vdots \\ \mathbb{E}_{X_D}[x_D] \end{bmatrix} \in \mathbb{R}^{D} \]

对于 $d = 1, \ldots, D$：
\[ \mathbb{E}_{X_d}[x_d] := \begin{cases} \int_{\mathcal{X}} x_d \, p(x_d) \, dx_d, & \text{如果 $X$ 为连续型随机变量}, \\[1em] \sum\limits_{x_i \in \mathcal{X}} x_i \, p(x_d = x_i), & \text{如果 $X$ 为离散型随机变量}. \end{cases} \qquad (6.32) \]

其中下标 $d$ 表示 $\boldsymbol{x}$ 对应的维度。上式是对随机变量 $X$ 的目标空间状态 $\mathcal{X}$ 的积分以及求和。

在一个维度中，还有另外两个直观的“平均”概念，即中位数 (median) 和众数 (mode)。
如果我们对这些值进行排序，中位数就是“最中间”的值，即 $50\%$ 的值大于中位数，$50\%$ 的值小于中位数。这一思想可以推广到连续值，考虑累计分布函数（定义 6.2）为 $0.5$ 的值。对于不对称或有长尾的分布，中位数提供了一个典型值的估计，该值比平均值更接近人类的直觉。此外，中位数对异常值的鲁棒性比平均值强。中位数向更高维度的推广是非平凡的，因为目前没有方法可以在不止一个维度中“排序” (Hallin et al., 2010; Kong and Mizera, 2012)。
众数 (mode)是最常出现的值。对于离散随机变量，众数定义为出现频率最高的 $x$ 的值。对于连续随机变量，众数定义为密度 $p(\boldsymbol{x})$ 上的一个峰值。一个特定的密度 $p(\boldsymbol{x})$ 可能有不止一个众数，而且在高维分布中可能有大量的众数。因此，找到一个分布的所有众数在计算上是具有挑战性的。

定义 6.3 定义了符号 $\mathbb{E}_X$ 的意义，作为一个算子，它表示我们应该取关于概率密度的积分（对于连续分布）或关于所有状态的和（对于离散分布）。均值的定义（定义 6.4），是期望值的一种特殊情况，通过取 $g$ 为恒等函数得到。

在一个维度中，还有另外两个直观的“平均”概念，即中位数（median）和众数（mode）。如果我们对这些值进行排序，中位数就是“最中间”的值，即 $50\%$ 的值大于中位数，$50\%$ 的值小于中位数。这一思想可以推广到连续值，考虑累计分布函数（定义 6.2）为 $0.5$ 的值。对于不对称或有长尾的分布，中位数提供了一个典型值的估计值，该值比平均值更接近人类的直觉。此外，中位数对异常值的鲁棒性比平均值强。中位数向更高维度的推广是非平凡的，因为目前没有方法可以在不止一个维度中“排序”Hallin2010,Kong2012。

众数（mode）是最常出现的值。对于离散随机变量，众数定义为出现频率最高的 $x$ 的值。对于连续随机变量，众数定义为密度 $p(x)$ 上的一个峰值。一个特定的密度 $p(x)$ 可能有不止一个众数，而且在高维分布中可能有大量的众数。因此，找到一个分布的所有众数在计算上是具有挑战性的。

众数是类似概率分布函数的局部最值吗？

协方差

对于两个随机变量，我们可以描述它们之间的对应关系。协方差直观地表示随机变量之间的相关性。

方差的概念是从协方差引出的，而不是相反！

协方差(一元)

两个单变量随机变量 $X, Y \in \mathbb{R}$ 之间的协方差（covariance）由其偏离各自均值的期望积给出，即
\[ \operatorname{Cov}_{X, Y}[x, y] := \mathbb{E}_{X, Y}\left[ \left(x - \mathbb{E}_{X}[x]\right)\left(y - \mathbb{E}_{Y}[y]\right) \right] \] 术语：多元随机变量的协方差 $\operatorname{Cov}[x, y]$ 有时被称为交叉协方差（cross-covariance），其中协方差指的是 $\operatorname{Cov}[x, x]$。

备注：
当与期望或协方差相关的随机变量的参数明确时，下标通常被去掉（例如，$\mathbb{E}_X[x]$ 经常被写成 $\mathbb{E}[x]$）。

利用期望的线性性，定义 6.5 中的表达式可以改写为乘积的期望值减去期望值的乘积，即
\[ \operatorname{Cov}[x, y] = \mathbb{E}[xy] - \mathbb{E}[x]\,\mathbb{E}[y] \] 一个变量与自身的协方差 $\operatorname{Cov}[x, x]$ 称为方差（variance），用 $\mathbb{V}_X[x]$ 表示。方差的平方根称为标准差（standard deviation），通常用 $\sigma(x)$ 表示。协方差的概念可以推广到多元随机变量。

定义 6.6 协方差（多元）

如果我们考虑两个多元随机变量 $\mathbf{X}$ 和 $\mathbf{Y}$，分别对应状态 $\mathbf{x} \in \mathbb{R}^D$ 和 $\mathbf{y} \in \mathbb{R}^E$，则 $\mathbf{X}$ 和 $\mathbf{Y}$ 之间的协方差定义为： \[ {Cov}[\mathbf{x}, \mathbf{y}] = \mathbb{E}\!\left[\mathbf{x} \mathbf{y}^{\top}\right] - \mathbb{E}[\mathbf{x}]\,\mathbb{E}[\mathbf{y}]^{\top} = \operatorname{Cov}[\mathbf{y}, \mathbf{x}]^{\top} \in \mathbb{R}^{D \times E}. \] 定义 6.6 可以应用于两个相同的多元随机变量，从而产生一个有用的概念，直观地捕捉随机变量的“扩散程度”。对于一个多元随机变量，方差描述了该随机变量的单个维度之间的关系。

方差与协方差矩阵 状态为 $\boldsymbol{x} \in \mathbb{R}^{D}$ 且均值向量为 $\boldsymbol{\mu} \in \mathbb{R}^{D}$ 的随机变量 $X$ 的方差 (variance) 定义为
\[ \begin{align} V_X[\boldsymbol{x}] &= \mathrm{Cov}_X[\boldsymbol{x}, \boldsymbol{x}] \\ &= \mathbb{E}_X \big[ (\boldsymbol{x} - \boldsymbol{\mu})(\boldsymbol{x} - \boldsymbol{\mu})^\top \big] \\ &= \mathbb{E}_X[\boldsymbol{x} \boldsymbol{x}^\top] - \mathbb{E}_X[\boldsymbol{x}] \ \mathbb{E}_X[\boldsymbol{x}]^\top \\ &= \begin{bmatrix} \mathrm{Cov}[x_1, x_1] & \mathrm{Cov}[x_1, x_2] & \cdots & \mathrm{Cov}[x_1, x_D] \\ \mathrm{Cov}[x_2, x_1] & \mathrm{Cov}[x_2, x_2] & \cdots & \mathrm{Cov}[x_2, x_D] \\ \vdots & \vdots & \ddots & \vdots \\ \mathrm{Cov}[x_D, x_1] & \mathrm{Cov}[x_D, x_2] & \cdots & \mathrm{Cov}[x_D, x_D] \end{bmatrix}. \end{align} \] 上式中的 $D \times D$ 矩阵称为多元随机变量 $X$ 的协方差矩阵 (covariance matrix)。协方差矩阵是对称的，且半正定，它描述了数据的扩散程度。协方差矩阵的对角线元素包含了边缘分布 \[ \begin{equation} p(x_i) = \int p(x_1, \ldots, x_D) \ \mathrm{d}x_{\backslash i} \end{equation} \] 的方差，其中符号 $\backslash i$表示“除了 $i$ 之外的所有变量”。非对角线元素为交叉协方差项 $\mathrm{Cov}[x_i, x_j]$，其中 $i, j = 1, \ldots, D, \ i \neq j$。

方差的三个表达式

1、方差的标准定义

与协方差的定义（定义6.5）相对应，是随机变量 $X$ 与其期望值 $\mu$ 的平方偏差的期望，即
\[ \begin{equation} \mathbb{V}_{X}[x] := \mathbb{E}_{X} \left[ (x - \mu)^{2} \right] \tag{6.43} \end{equation} \] 式（6.43）中的期望和平均值$\mu = \mathbb{E}_{X}(x)$使用（6.32）计算，取决于 $X$ 是离散的还是连续的随机变量。式（6.43）中表示的方差可以说是一个新的随机变量$Z := (X - \mu)^{2}$的均值。当根据经验估计（6.43）中的方差时，我们需要使用一个两阶段的算法：首先利用数据使用（6.41）计算平均值 $\mu$，然后使用这个估计值 $\hat{\mu}$ 计算方差。

2、事实证明，我们可以通过整理表达式来避免两个阶段。方差的标准定义： \[ \begin{equation} \mathbb{V}_{X}[x] := \mathbb{E}_{X}\left[(x-\mu)^2\right] \end{equation} \] （6.43）可以转换为所谓的“方差的原始分数公式”（raw-score formula for variance）： \[ \begin{equation} \mathbb{V}_{X}[x] = \mathbb{E}_{X}\left[x^2\right] - \left(\mathbb{E}_{X}[x]\right)^2 \qquad (6.44) \end{equation} \] (6.44)中的表达式可以这样记住：“平方的均值减去均值的平方”。这种方法只需对数据进行一次遍历计算，因为我们可以同时计算每个观测值 $x_i$ 的平均值 $\bar{x} = \frac{1}{n}\sum_i x_i$ 和平方平均值 $\frac{1}{n}\sum_i x_i^2$。

不幸的是，如果以这种方式计算，它在数值上可能不稳定，尤其是当 $x_i$ 的数值很大时，减法可能导致有效数字损失。

3、理解方差的第三种方式是，它可以表示为所有观测值对的差的总和。
考虑随机变量 $X$ 的一个样本 $x_1, \ldots, x_N$，我们计算 $x_i$ 和 $x_j$ 对之间的平方差。通过展开平方差，可以证明 $N^2$ 个观测值对的差的总和正好与观测值的经验方差相关： \[ \begin{equation} \frac{1}{N^2} \sum_{i,j=1}^{N} (x_i - x_j)^2 = 2 \left[ \frac{1}{N} \sum_{i=1}^{N} x_i^2 - \left( \frac{1}{N} \sum_{i=1}^{N} x_i \right)^2 \right] \qquad (6.45) \end{equation} \] 由此可见，(6.45) 是原始分数公式 (6.44) 的两倍。这意味着，我们可以用观测值两两之间的距离总和（$N^2$ 个）来表示偏离均值的偏离值总和（$N$ 个）。 从几何上来看，这意味着在一个点集中，点两两之间的距离总和与每个点到点集中心的距离总和是等价的。

随机变量的和与变换

均值和协方差在随机变量的仿射变换中表现出一些有用的特性。
假设随机变量 $\boldsymbol{X}$ 的均值向量为 $\boldsymbol{\mu}$，协方差矩阵为 $\boldsymbol{\Sigma}$，且 $\boldsymbol{X}$ 的（确定性）仿射变换为： \[ \boldsymbol{y} = \boldsymbol{A} \boldsymbol{x} + \boldsymbol{b} \] 由于 $\boldsymbol{y}$ 本身是一个随机变量，其均值向量和协方差矩阵分别为： \[ \begin{equation} \mathbb{E}_Y[\boldsymbol{y}] = \mathbb{E}_X[\boldsymbol{A}\boldsymbol{x} + \boldsymbol{b}] = \boldsymbol{A}\,\mathbb{E}_X[\boldsymbol{x}] + \boldsymbol{b} = \boldsymbol{A}\boldsymbol{\mu} + \boldsymbol{b} \qquad (6.50) \end{equation} \]

\[ \begin{equation} \mathbb{V}_Y[\boldsymbol{y}] = \mathbb{V}_X[\boldsymbol{A}\boldsymbol{x} + \boldsymbol{b}] = \mathbb{V}_X[\boldsymbol{A}\boldsymbol{x}] = \boldsymbol{A}\,\mathbb{V}_X[\boldsymbol{x}]\,\boldsymbol{A}^\top = \boldsymbol{A}\boldsymbol{\Sigma}\boldsymbol{A}^\top \qquad (6.51) \end{equation} \] 此外，$\boldsymbol{X}$ 与 $\boldsymbol{Y}$ 的协方差为： \[ \begin{align} \mathrm{Cov}[\boldsymbol{x}, \boldsymbol{y}] &= \mathbb{E}\big[\boldsymbol{x} (\boldsymbol{A}\boldsymbol{x} + \boldsymbol{b})^\top\big] - \mathbb{E}[\boldsymbol{x}]\,\mathbb{E}[\boldsymbol{A}\boldsymbol{x} + \boldsymbol{b}]^\top \\ &= \mathbb{E}[\boldsymbol{x}]\boldsymbol{b}^\top + \mathbb{E}[\boldsymbol{x}\boldsymbol{x}^\top]\boldsymbol{A}^\top - \boldsymbol{\mu}\boldsymbol{b}^\top - \boldsymbol{\mu}\boldsymbol{\mu}^\top \boldsymbol{A}^\top \\ &= (\mathbb{E}[\boldsymbol{x}\boldsymbol{x}^\top] - \boldsymbol{\mu}\boldsymbol{\mu}^\top)\,\boldsymbol{A}^\top = \boldsymbol{\Sigma}\,\boldsymbol{A}^\top \end{align} \] 其中，$\boldsymbol{\Sigma} = \mathbb{E}[\boldsymbol{x}\boldsymbol{x}^\top] - \boldsymbol{\mu}\boldsymbol{\mu}^\top$ 为 $\boldsymbol{X}$ 的方差矩阵。

(统计)独立性

独立推出不相关（协方差为0）

但这一点是充分不必然的，即，两个随机变量的协方差为零，但在统计上可能不独立。为了理解为什么，回想一下协方差是只能测量线性相关。而非线性相关的随机变量可能协方差也为零。

详见《协方差只反映线性相关.md》

随机变量的内积

把协方差作为内积的一个例子，协方差符合内积的定义。例如点积符合内积的定义一样。两个随机变量的“正交”就意味着它们协方差为零。具体的内积的定义见前文。在用协方差定义内积空间后，可以得出： \[ \|X\| = \sqrt{\mathbb{V}[X]} = \sigma[X] \] 这就是标准差。在普通向量空间里，向量长短衡量了它在空间中“延伸”的程度。在随机变量空间里，“长度”衡量的是它在概率空间中“波动”的程度。如果 $\sigma[X] = 0$，那么 $\mathbb{V}[X] = 0$，意味着 $X$ 在概率意义上是常数，不会随机变化。

如果我们考虑两个随机变量 $X$、$Y$ 之间的夹角 $\theta$，我们得到： \[ \begin{equation} \cos\theta = \frac{\langle X, Y \rangle}{\|X\|\,\|Y\|} = \frac{\operatorname{Cov}[x, y]}{\sqrt{\mathbb{V}[x]\,\mathbb{V}[y]}} \end{equation} \] 这是两个随机变量之间的相关性（定义 6.8）。这意味着，当我们从几何角度考虑两个随机变量时，可以把它们的相关性看作是两个随机变量之间夹角的余弦。

根据定义 3.7，我们知道：$X \perp Y \quad \Longleftrightarrow \quad \langle X, Y\rangle = 0$ 在我们的例子中，这意味着 $X$ 和 $Y$ 是正交的当且仅当：$\operatorname{Cov}[X, Y] = 0$即它们是不相关的。图 6.6 说明了这种关系。

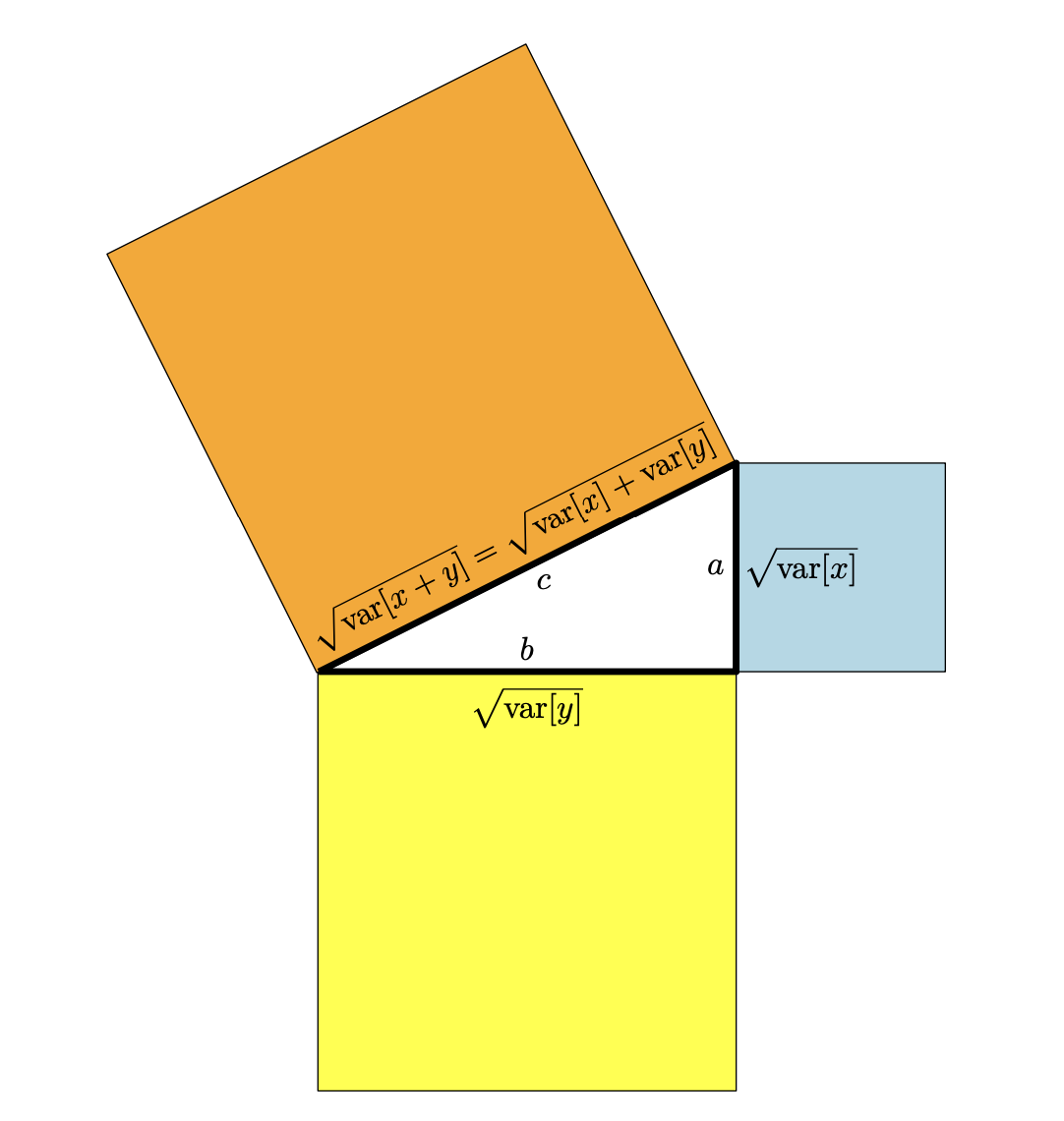
随机变量的几何

随机变量的几何。如果随机变量$X$和$Y$不相关，则它们是对应向量空间中的正交向量，且勾股定理也适用。

概率分布的距离定义

使用之前内积定义的欧几里得距离来比较概率分布似乎是个不错的选择，但不幸的是，这不是获得分布之间距离的最佳方法。回想一下，概率质量(或密度)是正的，需要加起来等于1。这些限制意味着分布存在于一种叫做统计流形(statistical manifold)的东西上。对概率分布空间的研究被称为信息几何( information geometry)。计算分布之间的距离通常使用Kullback-Leibler散度(KL散度)来完成，它是距离的推广，它解释了统计流形的性质。正如欧氏距离是矩阵的一种特殊情况一样(第3.3节)，KL散度是另外两种广义散度的一种特殊情况，它们被称为Bregman散度和f ff-散度。关于它们区别的研究超出了这本书的范围，读者可以参考信息几何领域的创始人之一Amari(2016)的新书了解更多细节。

具体的例子见《概率分布的距离定义.md》

高斯分布

由于高斯分布完全由其均值和协方差来表示，我们通常可以通过对随机变量的均值和协方差进行变换来得到变换后的分布。高斯分布的边缘分布和条件分布是高斯分布。高斯随机变量的任何线性/仿射变换后依然服从高斯分布。

共轭与指数族

在应用概率运算法则时，存在一些“封闭性”，如贝叶斯定理。封闭是指对一类对象应用特定操作后返回相同类型的对象。

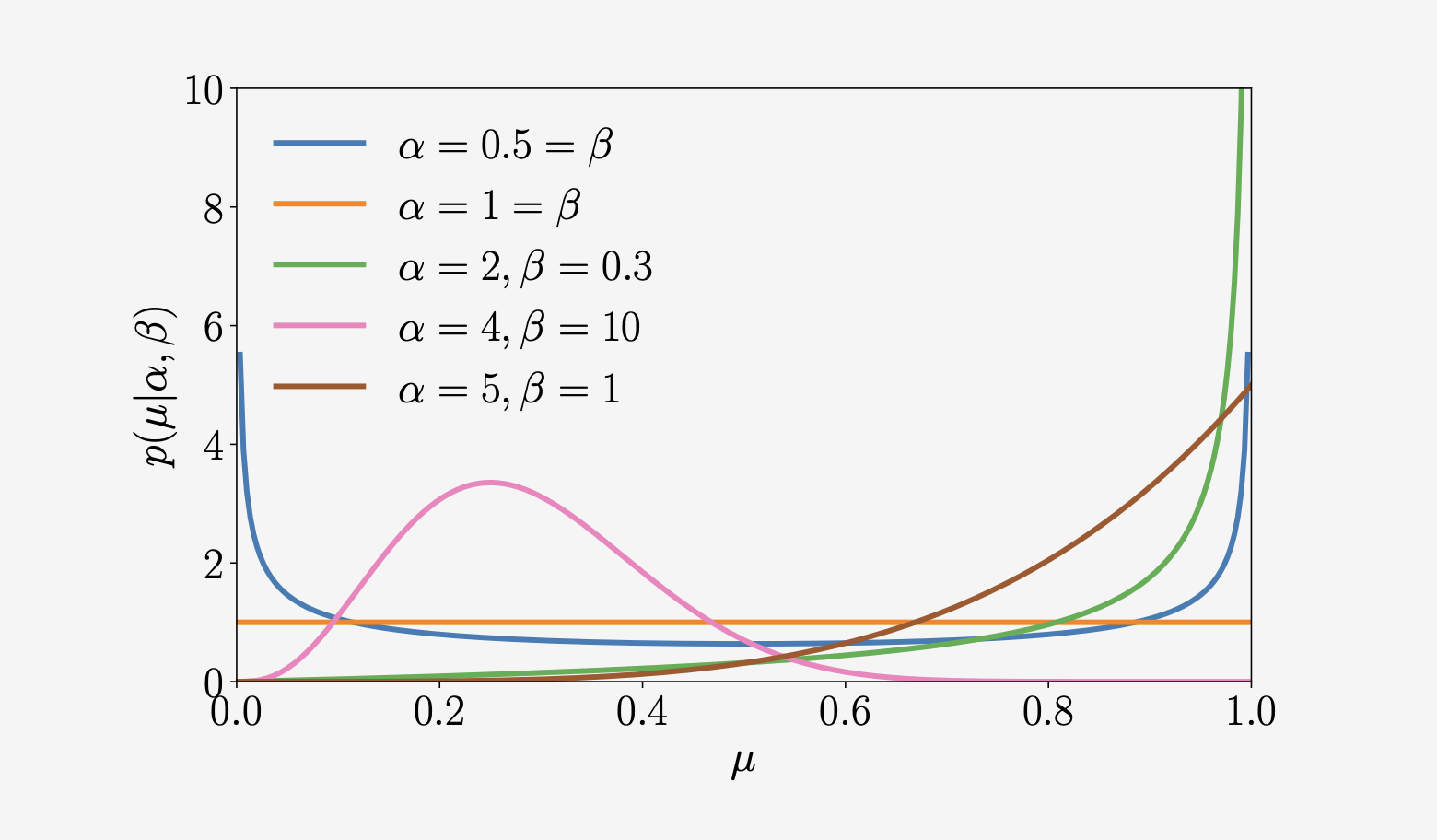
Beta分布

我们可能想在有限区间上建立一个连续随机变量的模型。Beta分布是一个连续随机变量 $\mu \in [0,1]$ 上的分布，通常用来表示一些二值事件的概率（例如，控制伯努利分布的参数）。Beta分布 $\mathrm{Beta}(\alpha, \beta)$（如图6.11所示）本身由两个参数控制 $\alpha > 0, \ \beta > 0$，并被定义为 \[ \begin{equation} p(\mu \mid \alpha, \beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \, \Gamma(\beta)} \, \mu^{\alpha-1} (1-\mu)^{\beta-1} \tag{6.98} \end{equation} \]

\[ \mathbb{E}[\mu] = \frac{\alpha}{\alpha+\beta}, \quad \mathbb{V}[\mu] = \frac{\alpha \beta}{(\alpha+\beta)^2 (\alpha+\beta+1)} \] 其中 $\Gamma(\cdot)$ 为伽马（Gamma）函数，定义为： \[ \Gamma(t) := \int_{0}^{\infty} x^{t-1} e^{-x} \, dx, \quad t > 0, \qquad \Gamma(t+1) = t \, \Gamma(t) \] 注意，（6.98）中的Gamma函数的分数标准化了Beta分布。

直观地看，$\alpha$ 将概率质量移向 $1$，而 $\beta$ 将概率质量移向 $0$。一些特殊的情况：

对于 $\alpha = 1 = \beta$，我们得到均匀分布 $\mathcal{U}[0,1]$。
对于 $\alpha, \beta < 1$，我们得到双峰分布，峰值在 $0$ 和 $1$ 处。
对于 $\alpha, \beta > 1$，分布是单峰的。
对于 $\alpha, \beta > 1$ 且 $\alpha = \beta$，分布是单峰对称的，且集中在区间 $[0,1]$，即均值在 $1/2$。

beta分布

有一大堆有名字的分布，它们以不同的方式相互联系(Leemis和McQueston, 2008)。值得记住的是，每个被命名的分布都是为了特定的原因而创建的，但是可能还有其他的应用。了解创建特定分布背后的原因可以知道如何最好地使用它。

共轭

共轭先验

如果后验与先验具有相同的形式/类型，则先验是似然函数的共轭(conjugate)。共轭特别方便，因为我们可以通过更新先验分布的参数来用代数方法计算后验分布。

备注： 在考虑概率分布的几何时，共轭先验保留了似然的距离结构(Agarwal and Daum´e III, 2010)

对于二项分布似然函数中的参数$\mu$，Beta先验是共轭的。Beta分布是伯努利分布的共轭先验。

常见似然函数的共轭先验

表6.2列出了一些用于概率建模的标准似然的参数的共轭先验。分布如多项式分布、逆Gamma分布、逆Wishart分布和Dirichlet分布可以在任何统计文本中找到，例如在Bishop(2006)中就进行了描述。

Beta分布是二项分布和伯努利分布似然中关于参数$\mu$的共轭先验。对于高斯似然函数，我们可以在均值上设置一个共轭高斯先验。高斯似然在表中出现两次的原因是我们需要区分一元和多元情况。在一元（标量）情况下，逆Gamma是方差的共轭先验。在多元情形下，我们使用逆Wishart分布作为协方差矩阵的共轭先验。Dirichlet分布是多项式似然函数的共轭先验。

指数族

分布三个抽象级别：

在考虑分布（离散或连续的随机变量）时，我们可以有三个可能的抽象级别。

在第一级（这是最具体的级别），我们有一个具有固定参数的特定“命名”分布，例如一个均值为零，方差为单位矩阵的一元高斯分布 $\mathcal{N}(0,1)$。

而在机器学习中，我们经常使用第二层抽象，即我们采用参数形式固定的分布（如一元高斯分布），并从数据中推断出它的参数。例如，我们假设一个未知均值 $\mu$ 和未知方差 $\sigma^2$ 的一元高斯分布 $\mathcal{N}\left(\mu, \sigma^{2}\right)$，并使用最大似然拟合来确定最佳参数 $(\mu, \sigma^2)$。我们将在第9章讨论线性回归时看到一个例子。

第三个抽象的层次是考虑分布的族，在本书中，我们考虑指数族。一元高斯分布是指数族中的一个例子。许多广泛使用的统计模型，包括表 6.2 中所有的“命名”模型，都属于指数族。它们都可以统一成一个概念。

我们研究指数族的主要动机是它们具有有限维的充分统计信息。此外，共轭分布很容易写出来，而且也来自一个指数族。从推理的角度来看，指数族的极大似然估计表现得很好，因为它的充分统计量的经验估计是充分统计量总体的最佳估计（回忆一下高斯分布的均值和协方差）。从优化的角度来看，指数族的的对数似然函数是凹的，允许我们应用有效的优化方法(第7章)。

变量替换/逆变换

似乎有很多已知的分布，但实际上，我们可以命名的分布是非常有限的。因此，理解随机变量在变换后是如何分布的通常很有用。例如，假设 $X$ 是根据一元正态分布 $\mathcal{N}(0,1)$ 得到的一个随机变量。那么 $X^2$ 的分布是什么？另一个在机器学习中很常见的例子是，假设 $X_1$ 和 $X_2$ 是一元标准正态分布，那么 $\frac{1}{2} (X_1 + X_2)$的分布是什么？计算 $\frac{1}{2} (X_1 + X_2)$ 的分布的一个选择是计算 $X_1$ 和 $X_2$ 的均值和方差，然后组合它们。正如我们在第 6.4.4 节中看到的，当我们考虑随机变量的仿射变换时，我们可以计算变换后得到的随机变量的均值和方差。然而，我们也可能无法得到变换后分布的函数形式。此外，我们还可能关心随机变量的非线性变换，这时变换后的封闭形式的表达式是不容易得到的。

我们将介绍两种通过随机变量变换获取分布的方法：一种是使用累积分布函数定义的直接方法，另一种是使用微积分的链式法则(第5.2.2节)的变量替换(change-of-variable)方法。变量替换方法被广泛使用，因为它提供了一个用于计算由于转换而产生的分布的“秘诀”。我们将解释关于一元随机变量的变量替换技术，并将简要地给出多元随机变量的一般情况的结果。

分布函数技术

均匀分布在统计中的重要性

基准分布：在随机数生成和蒙特卡罗模拟中，均匀分布是最常用的基础分布（大多数随机数生成器先生成 $U(0,1)$，再通过变换得到其他分布）。
概率积分变换：定理 6.15 就是基于这个思想：如果 $X$ 的 CDF 是严格单调的，那么 $Y = F_X(X)$ 服从 $U(0,1)$。

将随机变量$X$的累积分布函数$F_X(x)$作为变换函数$U(x)$，可以得到一个有用的结果,这导出了下面的定理。

定理 6.15 令 $X$ 为连续随机变量，且具有严格单调的累积分布函数 $F_X(x)$。那么定义为 \[ Y := F_X(X) \] 的随机变量 $Y$ 具有均匀分布。

证明：

对任意 $y\in[0,1]$，由于 $F_X$ 严格单调且连续，存在反函数 $F_X^{-1}:(0,1)\to \mathbb{R}$。于是 \[ \begin{aligned} F_Y(y) &:=\mathbb{P}(Y\le y) =\mathbb{P}\big(F_X(X)\le y\big) \\ &=\mathbb{P}\big(X\le F_X^{-1}(y)\big) =F_X\!\big(F_X^{-1}(y)\big) = y,\qquad y\in[0,1]. \end{aligned} \] 对区间外的 $y$，有 $F_Y(y)=0$（当 $y<0$）和 $F_Y(y)=1$（当 $y>1$）。因此 $F_Y(y)=y$（$y\in[0,1]$），即 $Y\sim \mathrm{Unif}(0,1)$。

定理6.15被称为概率积分变换(probability integral transform)，它用于推导从分布中采样的算法，这个算法通过均匀随机变量的采样结果进行变换（Bishop，2006）。该算法的工作原理是首先从均匀分布生成样本，然后通过逆累计密度函数（假设这是可以得到的）对其进行变换，以从所需分布获得样本。概率积分变换也用于假设检验样本是否来自特定分布（Lehmann和Romano，2005）。累积分布函数的输出是均匀分布的这一观点也构成了copulas的基础（Nelsen，2006）。

直观理解：

均匀分布随机数就像一个“百分比刻度”
逆 CDF 就是把这个刻度映射到目标分布的位置
这样就能用均匀分布随机数生成任何我们想要的分布样本

变量替换

区间可逆的函数要么严格递增要么严格递减。

事件的等价变换不会改变概率

微积分的基本定理中，有一个非常经典的结论：积分上限函数求导，它把导数与积分直接联系了起来。

详见《积分上限函数求导.md》。

备注：
“变量替换”这个名字来源于当我们面对一个困难的积分时改变积分变量的想法。对于一元函数，我们使用换元积分法：
\[ \begin{equation} \int f(g(x)) g^{\prime}(x)\, \mathrm{d}x = \int f(u)\, \mathrm{d}u, \quad \text{其中} \quad u = g(x) \qquad (6.133) \end{equation} \] 该法则的推导基于微积分的链式法则 (5.32)，以及应用两次微积分基本定理。微积分基本定理证明了积分和微分在某种程度上是互“逆”的。通过（松散地）考虑方程$u = g(x)$的微小变化（微分），即把$\Delta u = g^{\prime}(x)\, \Delta x$看作 $u = g(x)$ 的微分，可以直观地理解这个规则。将 $u = g(x)$ 代入，积分 (6.133) 右边的参数变成了 $f(g(x))$。通过假设 $\mathrm{d}u \approx \Delta u = g^{\prime}(x)\, \Delta x,\mathrm{d}x \approx \Delta x,$我们最终得到了 (6.133)。

定理 6.16:

令 $f(\boldsymbol{x})$ 是多变量连续随机变量 $\boldsymbol{X}$ 的概率密度函数。如果向量值函数 $\boldsymbol{y} = U(\boldsymbol{x})$在定义域内对于所有 $\boldsymbol{x}$ 可微且可逆，那么对应的随机变量 $\boldsymbol{Y} = U(\boldsymbol{X})$的概率密度函数由下式给出： \[ f(\boldsymbol{y}) = f_{\boldsymbol{x}}\bigl(U^{-1}(\boldsymbol{y})\bigr) \cdot \left|\frac{d}{d \boldsymbol{y}} U^{-1}(\boldsymbol{y})\right|, \] 其中 $\left|\frac{d}{d \boldsymbol{y}} U^{-1}(\boldsymbol{y})\right|$ 表示雅可比矩阵的行列式的绝对值。

这个定理的关键是多元随机变量的变量替换遵循单变量变量替换的过程。首先需要求出逆变换 $U^{-1}$，并将其代入 $\boldsymbol{x}$ 的密度函数 $f_{\boldsymbol{x}}(\boldsymbol{x})$ 中，然后计算雅可比矩阵的行列式，并与密度函数相乘得到结果。

连续优化

Continuous Optimization

由于机器学习算法是在计算机上实现的，其中许多数学方程式都表示为数值优化方法。本章描述了训练机器学习模型的基本数值方法。训练机器学习模型通常归结为找到一组好的参数。“好”的概念是由目标函数或概率模型来决定的，我们将在本书的第二部分看到这些例子。给定一个目标函数，使用优化算法来寻找最佳值。$ ^{D}$ 中考虑数据和模型，所以我们面临的优化问题是连续优化问题，而不是离散变量的组合优化问题。

一般情况下，机器学习中的大多数目标函数都是要被最小化的，即最优值就是最小值。直观上，梯度为目标函数每个点的上坡方向，而我们的目的是下坡（与梯度方向相反），希望找到最深的点。

我们将学习一类称为凸函数的函数，它们对优化算法的起点没有依赖性。对于凸函数，局部最小值就是全局最小值。事实证明，许多机器学习目标函数的设计都是凸的.

一般研究最小值，所以对应研究的也是凸函数。

使用梯度下降法优化

梯度下降法是一种一阶优化算法。为了用梯度下降法寻找函数的局部最小值，我们取与函数在当前点的梯度的一定比例的负值调整$x$。回想第5.1节，梯度指向最陡的上升方向。另一个直观的表现是考虑函数的等高线。梯度指向与我们希望优化的函数的等高线正交的方向。

梯度一定是指向上升的方向：

严格来说，梯度确实指向函数在某一点上“最陡上升”的方向。梯度的符号和大小告诉我们函数值局部上升最快的方向和速率。对于一元函数，梯度的正负直接指明函数上升的方向。

梯度的几何意义

梯度方向是函数值增加最快的方向。

梯度的大小 $\|\nabla f(\boldsymbol{x})\|$ 表示该方向上函数上升的速率。

如果沿着梯度的负方向移动 $-\nabla f(\boldsymbol{x})$，则是下降最快的方向（常用于梯度下降算法）。

梯度是函数上升最快的方向。但它只描述局部方向，想找最大值还需要结合函数整体信息。

例如 $y=x^2$,导数是$2x$，针对负轴，导数<0;所以沿$x$轴负方向是函数值上升最快的方向，反之也能推导出。

自适应梯度方法能根据函数的局部性质，在每次迭代时重新调整步长。有两种简单的方法（Toussaint，2012）：

当采用梯度下降后函数值增大了，则表明步长过大了。这时我们可以撤消并减小步长。
当函数值减小时，我们可以尝试增大步长。

尽管“撤消”步骤似乎是浪费资源，但使用这种启发式方法可以保证单调收敛。

动量梯度下降：

如图7.3所示，如果优化的曲面的存在缩放效果不佳的区域，那么梯度下降的收敛速度可能非常慢。改进收敛性的一个方法是给梯度下降添加记忆项。动量梯度下降法（Rumelhart et al.，1986）引入了附加项来记忆上一次迭代中发生了什么。这种记忆可以抑制振荡，平滑梯度更新。继续用球做类比，动量项模拟了重球从斜坡滚下不会轻易改变方向的现象。其思想是使用记忆进行梯度更新，以实现滑动平均( moving average)。基于动量的方法记忆了每次迭代的更新量$\Delta \boldsymbol{x}_{i}$,下一次更新则用当前和之前梯度的线性组合确定：

随机梯度下降法：

计算梯度非常耗时。然而，通常可以找到梯度的“cheap”近似值。只要近似梯度指向与真实梯度大致相同的方向，那么它就是有用的。

随机梯度下降法（Stochastic gradient descent，通常简称为SGD）是梯度下降法的一种随机近似方法，用于最小化目标函数，且目标函数应是可微函数之和。这里的“随机”一词指的是这样一个事实，即我们承认我们并不精确地知道梯度，而是只知道它的噪声近似值。通过约束近似梯度的概率分布，我们仍然可以从理论上保证SGD收敛。

如前所述，标准梯度下降法是一种“批量”优化方法，即选取合适的步长参数 $gamma_i$，并使用所有训练集，然后通过以下公式更新向量参数： \[ \boldsymbol{\theta}_{i+1} = \boldsymbol{\theta}_{i} - \gamma_{i} \left( \nabla L(\boldsymbol{\theta}_{i}) \right)^{\top} = \boldsymbol{\theta}_{i} - \gamma_{i} \sum_{n=1}^{N} \left( \nabla L_{n}(\boldsymbol{\theta}_{i}) \right)^{\top} \qquad (7.15) \] 求梯度和可能需要对所有$L_n$的梯度进行计算。当训练集是巨大的，或者（并且）损失函数不是简单的公式时，计算梯度和需要消耗巨大的计算资源。

考虑 (7.15) 中的$\sum_{n=1}^{N}\left(\nabla L_{n}\left(\boldsymbol{\theta}_{i}\right)\right),$我们可以取较小的 $L_n$ 集合来求它们的梯度和以减少计算量。与批量梯度下降法使用 $n=1,\ldots,N$ 的所有 $L_n$ 不同，小批量梯度下降随机选取 $L_n$ 的子集。在极端情况下，我们还可以随机选择一个 $L_n$ 来估计梯度。

关于为什么选取数据子集是明智的，关键的见解是要认识到，为了使梯度下降收敛，我们只要求梯度是真实梯度的无偏估计。事实上，(7.15) 中的$\sum_{n=1}^{N}\left(\nabla L_{n}\left(\boldsymbol{\theta}_{i}\right)\right)$是梯度期望值（第 6.4.1 节）的经验估计。因此，对期望值的任何其他无偏经验估计，例如使用数据的任何子样本，将足以使梯度下降收敛。

备注： 当学习率以适当的速率下降时，在相对不严格的假设下，随机梯度下降必然收敛到局部最小值（Bottou, 1998）。

为什么要考虑使用近似梯度？一个主要原因是硬件的限制，例如中央处理器（CPU）/图形处理器（GPU）内存大小或计算时间的限制。我们可以像在估计经验平均数时考虑样本的大小一样（第 6.4.1 节），来考虑用来估计梯度的子集的大小。较大的小批量将提供准确的梯度估计，减少参数更新中的方差。此外，较大的小批量可以使代价和梯度向量化，从而能使用高度优化的矩阵运算。方差的减少导致更稳定的收敛性，但每次梯度计算的计算量都很大。

相比之下，较小的小批量可以很快估计。如果我们保持较小的小批量，梯度估计中的噪声将允许我们脱离局部最优解。在机器学习中，优化方法是利用训练数据，通过最小化目标函数来进行训练的，但总体目标是提高泛化性能（第 8 章）。由于机器学习的目标不一定需要精确估计目标函数的最小值，所以使用小批量方法的近似梯度被广泛使用。

约束优化与拉格朗日乘子

拉格朗日对偶( Lagrangian duality)的概念。一般来说，对偶优化的思想是将一组变量$\boldsymbol{x}$（称为原始变量）的优化问题转化为另一组变量$\boldsymbol{\lambda}$（称为对偶变量）的优化问题。我们将会介绍两种不同的对偶方法：在本节中，我们讨论的是拉格朗日对偶；在第7.3.3节中，我们将讨论Legendre-Fenchel对偶。

对偶问题计算上的好处

有时原问题不好解，但对偶问题更容易（例如约束简单、凸结构更明显）。

在大规模问题（如支持向量机 SVM）中，通常是通过对偶问题求解的。

不等式约束对应的拉格朗日乘子约束为非负，而等式约束对应的拉格朗日乘子则不加约束。

通过引入与每个不等式约束分别对应的拉格朗日乘子 $\lambda_i \geq 0$ （Boyd 和 Vandenberghe，2004，第 4 章），得到：

\[ \begin{equation} \mathfrak{L}(\boldsymbol{x}, \boldsymbol{\lambda}) = f(\boldsymbol{x}) + \sum_{i=1}^{m} \lambda_i g_i(\boldsymbol{x}) = f(\boldsymbol{x}) + \boldsymbol{\lambda}^{\top} \boldsymbol{g}(\boldsymbol{x}) \qquad (7.20) \end{equation} \]

其中我们将所有约束 $g_i(\boldsymbol{x})$ 写成一个向量 $\boldsymbol{g}(\boldsymbol{x})$；把所有拉格朗日乘子也写成向量 $\boldsymbol{\lambda} \in \mathbb{R}^{m}$。

我们现在介绍拉格朗日对偶 (Lagrangian duality)}的概念。一般来说，对偶优化的思想是将一组变量 $\boldsymbol{x}$（称为原始变量）的优化问题转化为另一组变量 $\boldsymbol{\lambda}$（称为对偶变量）的优化问题。 定义7.1 问题 \[ \begin{equation} \min_{\boldsymbol{x}} f(\boldsymbol{x}) \quad \text{subject to} \quad g_i(\boldsymbol{x}) \leqslant 0, \quad i=1,\ldots,m \end{equation} \] 被称为原始问题 (primal problem)，对应原始变量 $\boldsymbol{x}$。

与它对应的拉格朗日对偶问题 (Lagrangian dual problem)由下式给出： \[ \begin{equation} \max_{\boldsymbol{\lambda} \in \mathbb{R}^m} \; \mathfrak{D}(\boldsymbol{\lambda}) \quad \text{subject to} \quad \boldsymbol{\lambda} \geqslant \mathbf{0}, \end{equation} \] 其中 $\boldsymbol{\lambda}$ 为对偶变量，且 \[ \begin{equation} \mathfrak{D}(\boldsymbol{\lambda}) = \min_{\boldsymbol{x} \in \mathbb{R}^d} \; \mathfrak{L}(\boldsymbol{x}, \boldsymbol{\lambda}). \end{equation} \]

凸优化

让我们我们重点讨论一类特别有用的优化问题上，因为在这类问题上我们可以保证得到全局最优解。目标函数$f(·)$是一个凸函数，且约束$g(·)$和$h(·)$是凸集的问题称为凸优化问题( convex optimization problem)。在这种情况下，称它具有强对偶性(strong duality)：对偶问题的最优解与原问题的最优解相同。在机器学习文献中，凸函数和凸集通常是不严格区别的，但是人们通常可以从上下文中推断出隐含的含义。

凸函数的非负加权和是凸的.

线性规划

考虑所有函数都是线性的特殊情况，即： \[ \begin{equation} \min_{\boldsymbol{x} \in \mathbb{R}^{d}} \boldsymbol{c}^{\top} \boldsymbol{x} \qquad (7.39) \end{equation} \]

\[ \text{subject to } \quad \boldsymbol{A}\boldsymbol{x} \leqslant \boldsymbol{b} \] 其中 $\boldsymbol{A} \in \mathbb{R}^{m \times d}, \ \boldsymbol{b} \in \mathbb{R}^{m}$。

取 $\mathfrak{L}(\boldsymbol{x}, \boldsymbol{\lambda})$ 对 $\boldsymbol{x}$ 的导数并将其设为零(因为是$x$的一次函数，求导消去了$x$)，得到对偶优化问题，是关于$\lambda$的线性规划问题，但有$m$个变量。我们可以选择求解原始规划问题（7.39）或其对偶规划问题（7.43），这取决于$m$和$d$哪个更大。

二次规划

考虑凸二次目标函数的情况，其中约束是仿射的，即： \[ \min_{\boldsymbol{x} \in \mathbb{R}^{d}} \frac{1}{2} \boldsymbol{x}^{\top} \boldsymbol{Q} \boldsymbol{x} + \boldsymbol{c}^{\top} \boldsymbol{x} \]

\[ \text{subject to} \quad \boldsymbol{A}\boldsymbol{x} \leqslant \boldsymbol{b} \] 其中 $\boldsymbol{A} \in \mathbb{R}^{m \times d},\ \boldsymbol{b} \in \mathbb{R}^{m},\ \boldsymbol{c} \in \mathbb{R}^{d}$。

对称方阵 $\boldsymbol{Q} \in \mathbb{R}^{d \times d}$ 是正定的，因此目标函数是凸的。这就是所谓的二次规划。注意它有 $d$ 个变量和 $m$ 个线性约束。

一般定义二次规划（QP）时，只要求 $Q$ 半正定（positive semidefinite, PSD），这样目标函数就是凸的；

同线性规划，取 $\mathfrak{L}(\boldsymbol{x}, \boldsymbol{\lambda})$ 对 $\boldsymbol{x}$ 的导数，并将其设为零(因为是$x$的二次函数，求导得到关于$x$的一次方程，可以用$\lambda$替换$x$代入对耦优化问题)，得到对偶优化问题，是关于$\lambda$的二次规划问题。

Legendre-Fenchel变换和凸共轭

这一节没深入看！

信息论

原书里面找不到这一章？

称为随机变量$X$的信息熵(Entropy)。自信息用单个事件的结果计算。而熵来对整个概率分布中的平均不确定性进行量化，是从平均意义上表征随机变量总体特性的一个量。换言之，一个分布的熵是指服从这个分布的随机变量所能产生的期望信息总量。

导言

为直觉寻找词语

线性代数

线性方程求解

群

线性变换的定义

变换矩阵

相似矩阵

恒等映射

基变换

变量变换和基变换的矩阵区别

像与核

仿射空间

仿射映射

解析几何

范数

内积

正定矩阵

长度和距离

距离和度量

角度和正交

正交矩阵

函数的内积

正交投影

旋转

矩阵分解

行列式与迹

特征值和特征向量

谱定理

特征值、特征向量、行列式、迹的联系

矩阵分解

Cholesky分解

特征值分解与对角化

奇异值分解

特征值分解 vs. 奇异值分解

矩阵逼近

矩阵分类关系图

向量微积分

泰勒级数

微分法则

偏微分与梯度

链式法则

多变量链式法则

向量值函数的梯度

反向传播与自动微分法

概率与分布

概率空间 \((\Omega, \mathcal{A}, P)\)，

加法法则、乘法法则和贝叶斯定理

期望值

协方差

相关

方差的三个表达式

随机变量的和与变换

(统计)独立性

随机变量的内积

概率分布的距离定义

高斯分布

共轭与指数族

Beta分布

共轭

指数族

变量替换/逆变换

分布函数技术

变量替换

连续优化

使用梯度下降法优化

动量梯度下降：

随机梯度下降法：

约束优化与拉格朗日乘子

凸优化

线性规划

二次规划

Legendre-Fenchel变换和凸共轭

信息论