《统计学习基础》 (3/6)
读书笔记之三:第5章-第7章
第五章:基函数扩展与正则化; 第六章:核平滑方法; 第七章:模型评估与选择。
第五章 基函数扩展与正则化
- 据说三次样条是人眼看不出结点不连续的最低阶样条.很少有更好的理由去选择更高次的样条,除非对光滑的微分感兴趣.
- 固定结点的样条也称作 回归样条 (regression
splines).我们需要选择样条的阶数,结点的个数以及它们的位置.一种简单方式是用基函数或自由度来参量化样条族,并用观测
\(x_i\) 来确定结点的位置.
- 自然三次样条 (natural cubic spline)
添加额外的限制,具体地,令边界结点之外的函数是线性的.
- 高维特征的预处理是非常普遍的而且对于改善学习算法的效果是很有效的。
第六章 核平滑方法
- \(\Vert \cdot\Vert\)
是欧几里得范数.因为欧式范数取决于每个坐标的单位,所以对每个预测变量进行标准化是有意义的,举个例子,在光滑之前,标准化为单位标准误差.
- 当维度与样本大小的比率不是很好,则局部回归对我们没有太大帮助,除非我们想要对模型做出一些结构化的假设.这本书的很多部分是关于结构化回归和分类模型的.
6.1 朴素贝叶斯分类器
不管它的名字(也称为“白痴的贝叶斯”!),这是这些年仍然流行的技巧.当特征空间的维数 \(p\) 很高,这种方式特别合适,使得密度估计不再吸引人.朴素贝叶斯模型假设给定类别 \(G=j\),特征 \(X_k\) 是独立的:
\[ f_j(X)=\prod\limits_{k=1}^pf_{jk}(X_k)\tag{6.26}\label{6.26} \]
尽管这个假设一般是不对的,但是确实很大程度上简化了估计:
- 单独的类别条件的边缘密度 \(f_{jk}\) 可以采用一维核密度估计分别估计出来.这实际上是原始朴素贝叶斯过程的泛化,采用单变量高斯分布来表示这些边缘密度.
- 如果 \(X\) 的组分 \(X_j\) 是离散的,则可以使用合适的直方图估计.这提供了在特征向量中混合变量类型的完美方式.

尽管这些假设过于乐观,朴素贝叶斯分类器经常比更复杂的分类器做得更好.原因与图 6.15 相关:尽管单独的类别密度估计可能是有偏的,但这个偏差或许不会对后验概率不会有太大的影响,特别是在判别区域附近.实际上,这个问题或许可以承受为了节省方差造成的相当大的偏差,比如“天真的”假设得到的.
6.2 计算上的考虑
核和局部回归以及密度估计都是 基于内存的 (memory-based) 方法:模型是整个训练数据集,并且在赋值或者预测的时候完成拟合.对于许多实时的应用,这使得这类方法不可行.
第七章 模型评估与选择
根据百度百科 即 知乎回答,定距变量也称间距变量,是取值具有“距离”特征的变量。统计学依据数据的计量尺度将数据分为四大类:
- 定距型 (interval scale): 数值变量,可以加减运算,但不能乘除;不存在基准 0 值,即当变量值为 0 时不是表示没有,如温度变量。
- 定序型 (ordinal scale): 类别型变量,如性别。
- 定类型 (nominal scale): 不可以做四则运算,如满意度(非常满意、满意、一般、不满意、非常不满意)。
- 定比型 (ratio scale): 数值变量,存在 0 值,比值有意义。
7.1 测试误差和训练误差
7.1.1 测试误差和期望测试误差
测试误差 (test error),也被称作 泛化误差 (generalization error),它是在独立的测试样本上的预测误差 \[ \text {Err}_{\cal T}=E[L(Y,\hat f(X))\mid {\cal T}]\tag{7.2} \]
其中 \(X\) 和 \(Y\) 都是随机从它们的(总体)联合分布中选取的.这里训练集 \(\cal T\) 是固定的,测试误差指的是对该特定训练集的误差.一个相关的量是 期望预测误差 (expected prediction error)(或者 期望测试误差 (expected test error))
\[ \text {Err} = E[L(Y,\hat f(X))]=\text {E}[\text {Err}_{\cal T}]\tag{7.3} \]
注意到这个期望平均的任何项都是随机的,包括产生 \(\hat f\) 的训练集的随机性.
7.1.2 训练误差
训练误差 (Training error) 是在训练样本上的平均损失,(注意:这里是平均值) \[ \overline{\text {err}}=\frac{1}{N}\sum\limits_{i=1}^NL(y_i,\hat f(x_i))\,.\tag{7.4} \]
我们想要知道估计模型 \(\hat f\) 的测试误差的期望值.当模型越来越复杂时,它使用更多的训练数据并且可以适应于更复杂的潜在结构.因此偏差会有降低而方差会有增大.一些中等程度的模型复杂度给出了最小的测试误差期望值.
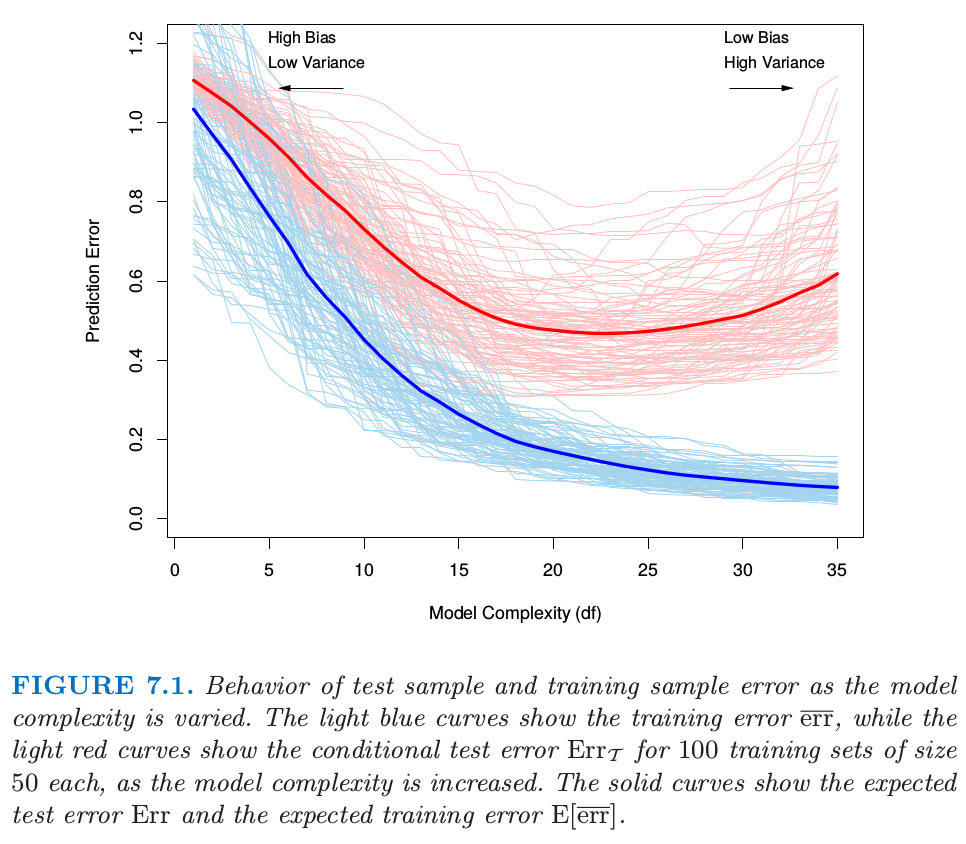
不幸的是,正如我们在图 7.1 中看到的那样训练误差不是测试误差一个良好的估计.训练误差随着模型复杂度增大不断降低,一般地如果我们将模型复杂性增到充分大它会降为 0.然而,0 训练误差的模型对训练数据是过拟合的并且一般泛化性很差.
7.2 模型选择
重要的是要注意,事实上我们可能有两个单独的目标:
模型选择 (Model selection): 估计不同模型的表现来选择最好的那个
模型评估 (Model assessment): 已经选择好了最终模型,估计它在新数据上的预测误差(泛化误差)
如果我们处在有充足数据的情形中,对于这两个问题的最好的方式是将数据集随机地分成 3 个部分:训练集,验证集,以及测试集.训练集用来拟合模型;验证集用来估计预测误差来进行模型选择;测试集用来评估最终选择的模型的泛化误差.理想情形下,测试集应保存在“黑箱 (valut)”中,并且只在数据分析结束时才会显示出来.否则,假设我们重复采用测试集,选择具有最小测试误差的模型,则最终选择模型的测试误差会低估真实的测试误差,有时候偏差是相当大的.
在三个部分的每一个中如何选取观测的个数很难给出一个一般性的规则,因为这取决于数据的信噪比和训练样本的规模.一般的分割是 50% 用于训练,25% 用于验证,25% 用于测试:
本章中的方法是为了没有足够的数据来分成 3 部分的情形设计的.同样地,给出多少的训练数据是足够的一般规则太难了;此外,这取决于潜在函数的信噪比以及根据数据拟合出的模型的复杂度.
本章的方法有两类,第一类通过分析的手段 (AIC,BIC,MDL,SRM),第二类通过有效的样本重利用(交叉验证和自助法)来近似验证过程(验证过程即比较候选模型选出最优的模型).除了在模型选择使用它们,我们也检验了每个方法对最终选择的模型的测试误差的估计的可靠性程度.
在讨论这些之前,我们首先进一步探究测试误差的本质与 偏差-方差之间的权衡 (the bias-variance tradeoff).
7.2.1 偏差-方差分解
和 第 2 章一样,如果我们假设 \(Y=f(X)+\varepsilon\),其中 \(\text {E}(\varepsilon)=0\),并且 \(\text {Var}(\epsilon)=\sigma_\varepsilon^2\),我们可以导出在使用平方误差损失的情形下,在输入点 \(X=x_0\) 处回归拟合值 \(\hat f(X)\) 的期望预测误差:(个人注:这里是对单独的点,而不是MSE) \[ \begin{align} \text {Err}(x_0)&=\text {E}[(Y-\hat f(x_0))^2\mid X=x_0]\notag\\ &=\sigma_\varepsilon^2+[\text {E}\hat f(x_0)-f(x_0)]^2+\text {E}[\hat f(x_0)-E\hat f(x_0)]^2\notag\\ &=\sigma_\varepsilon^2+\text {Bias}^2(\hat f(x_0))+\text {Var}(\hat f(x_0))\notag\\ &=\text{Irreducible Error} + \text{Bias}^2+\text{Variance} \quad(7.9) \end{align} \]
第一项是目标在真实均值 \(f(x_0)\) 处的方差,无论我们对 \(f(x_0)\)(个人注:观测的数据?) 的估计有多好,这是不可避免的,除非 \(\sigma_\varepsilon^2=0\),第二项是偏差的平方,是我们估计的均值与真实的均值间的偏差量;最后一项是方差,是估计的 \(\hat f(x_0)\) 在其均值处的平方偏差的期望值.
一般地,我们建立的模型 \(\hat f\) 越复杂,(平方)偏差越低但是方差越大。
对于线性模型族比如岭回归,我们可以更精细地分解偏差。
接着我们可以将 偏差平方的平均 (average squared bias) 写成 \[ \begin{align} &\text {E}_{x_0}[f(x_0)-E\hat f_\alpha(x_0)]^2\notag\\ &=\text {E}_{x_0}[f(x_0)-x_0^T\beta_*]^2+\text {E}_{x_0}[x_0^T\beta_*-\text {E} x_0^T\hat\beta_\alpha]^2\notag\\ &=\text{Ave[Model Bias]}^2+\text{Ave[Estimation Bias]}^2 \quad(7.14) \end{align} \]
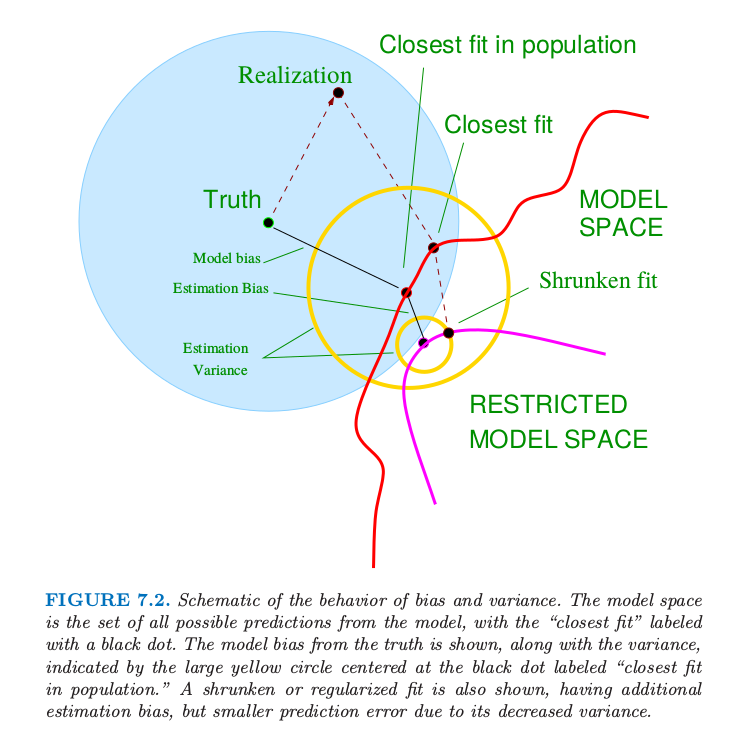
右侧的第一项是 模型偏差 (model bias) 平方的平均,它是最优线性近似和真实函数之间的误差.第二项是 估计偏差 (estimation bias) 平方的平均,它是估计的平均值 \(\text {E}(x_0^T\hat\beta)\) 与最优线性近似之间的误差.
对于通过普通最小二乘拟合的线性模型,估计量的偏差为 0.对于约束的拟合,比如岭回归,它是正的,而且我们用减小方差的好处进行交易.模型偏差只可能通过将线性模型类扩大为更广的模型类才能降低,或者通过在模型中加入变量的交叉项以及变换项(通过变量的变换得到的)来降低。
详见原书图7.2!
偏差方差间的权衡在 0-1 损失的表现与在平方误差损失的表现不一样.反过来意味着调整参数的最优选择可能在两种设定下本质上不同.正如后面章节中描述的那样,我们应该将调整参数的选择建立于对预测误差的估计之上。
7.2.2 训练误差率的 optimism
训练误差 (training error)
\[ \overline{\text {err}} = \frac{1}{N}\sum\limits_{i=1}^NL(y_i,\hat f(x_i))\tag{7.17}\label{7.17} \]
会比真实误差 \(\text {Err}\_{\cal T}\) 小,因为数据被同时用来拟合方法并且评估误差(见练习 2.9).拟合方法一般适应于训练数据,因此 表面误差 (apparent error) 或训练误差 \(\overline{\text {err}}\) 是对泛化误差 \(\mathrm {Err}\_{\cal T}\)过度的乐观估计。
7.2.3 交叉验证
错误的方式: 考虑有许多预测变量的分类问题,举个例子,可能在基因与蛋白质的应用中.一般的分析技巧或许如下:
- 筛选预测变量:选择与类别有着相当强(单变量)相关性的“好”预测变量的一个子集
- 运用这个预测变量的子集,建立多维变量分类器.
- 采用交叉验证来估计未知调整参数并且估计最终模型的预测误差.
这是正确地应用交叉验证吗?
正确的方式: 下面是在这个例子中正确使用交叉验证的方式:
将样本随机分成 \(K\) 个交叉验证折(群).
对于每一折 \(k=1,2,\ldots,K\)
1). 利用除了第 \(k\) 折的所有样本找到与类别标签有相对强(单变量)的相关性的“好”预测变量的一个子集.
2). 利用除了第 \(k\) 折的所有样本仅仅运用找到的预测变量来建立多元分类器.
3). 运用分类器来预测第 \(k\) 折中样本的类别.
7.2.4 自助法
自助法我觉得是最“独立”,最“自强”的方法了。
所以这也是我最喜欢的统计方法了。
自助法是评价统计精确性的通用工具。
基本思想是从训练集中有放回地随机选取数据集,每个样本的大小与原始数据集相同.做 \(B\) 次(如 \(B=100\))选取的操作,得到 \(B\) 个自助训练集。接着我们对每个自助法数据集重新拟合模型,并且检验在 \(B\) 个复制集上拟合的表现.
我们的结论是,对于这些特定的问题和拟合方法,AIC 和交叉验证的最小化,或者自助法都得到相当接近最好的可行模型.注意到模型选择的目的,这些衡量方式可能都有偏差,但是这不会有影响,只要偏差不会改变这些方法的相对表现.举个例子,对所有的衡量方式都加上常数不会改变最终选择的模型.然而,对于许多自适应非线性技巧(比如树),估计参数的有效个数是非常困难的.这使得像 AIC 之类的方法不可行,只留下交叉验证和自助法供我们选择.
全书的读书笔记(共6篇)如下:
《统计学习基础》读书笔记之一
《统计学习基础》读书笔记之二
《统计学习基础》读书笔记之三
《统计学习基础》读书笔记之四
《统计学习基础》读书笔记之五
《统计学习基础》读书笔记之六