《统计学习基础》 (4/6)

第八章：模型推断与平均化； 第九章：加性模型、树模型及相关方法； 第十章：提升方法与加性树模型。

第八章 模型推断与平均化

本书的大部分章节中，对于回归而言，模型的拟合（学习）通过最小化平方和实现；或对于分类而言，通过最小化交叉熵实现．事实上，这两种最小化都是用极大似然来拟合的实例。

这章中，我们给出极大似然法的一个一般性的描述，以及用于推断的贝叶斯方法．在第7章中讨论的自助法在本章中也继续讨论，而且描述了它与极大似然和贝叶斯之间的联系．最后，我们提出模型平均和改善的相关技巧，包括 committee 方法、bagging、stacking 和 bumping．

8.1 自助法和最大似然法

• 自助法，通过从训练集中有放回地采样，称作非参自助法(nonparametric bootstrap),这实际上意味着这个方法是与模型无关的，因为它使用原始数据来得到新的数据集，而不是一个特定的含参数的模型．
• 本质上自助法是非参最大似然或者参数最大似然法的计算机实现．与最大似然法相比自助法的好处是允许我们在没有公式的情况下计算标准误差和其他一些量的最大似然估计． （详见原书的图8.2）

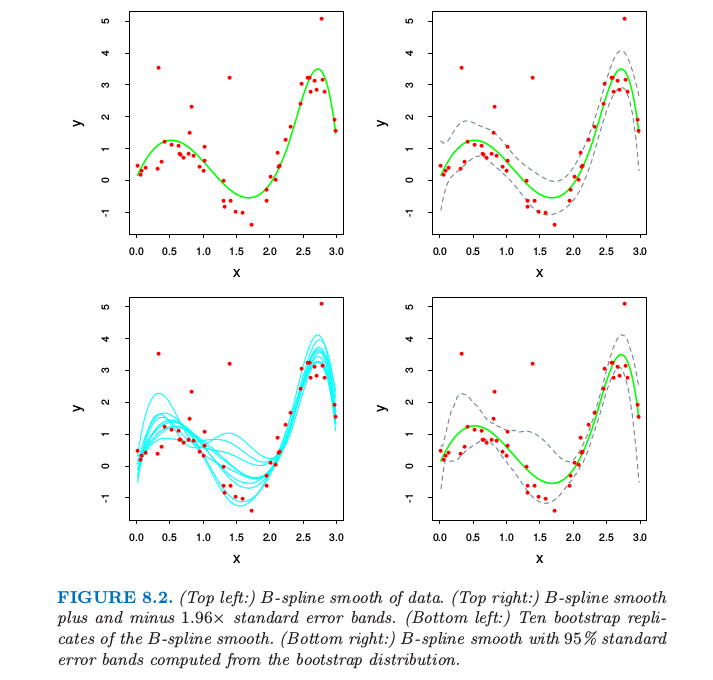
8.2 贝叶斯方法

• 贝叶斯方法与一般推断方法的不同之处在于，用先验分布来表达知道数据之前的这种不确定性，而且在知道数据之后允许不确定性继续存在，将它表示成后验分布．

• 最大似然方法会使用在最大概率估计那个点的密度来预测未来的数据．不同于贝叶斯方法的预测分布，它不能说明估计 \(\theta\) 的不确定性。

  个人注：推断中最大似然是预测某个最大的\(\theta\)值，贝叶斯方法是预测\(\theta\)的分布？

• 自助法分布表示我们参数的（近似的）非参、无信息后验分布．但是自助法分布可以很方便地得到——不需要正式地确定一个先验而且不需要从后验分布中取样．因此我们或许可以把自助法分布看成一个“穷人的”贝叶斯后验．通过扰动数据，自助法近似于扰动参数后的贝叶斯效应，而且一般实施起来更简单．

8.3 EM算法

EM 算法是简化复杂极大似然问题的一种很受欢迎的工具；

个人注：入门的视频见B站 博主“风中摇曳的小萝卜”的视频“EM算法 你到底是哪个班级的”

8.4 Bagging

简单来说，bagging 和随机森林都是针对 bootstrap 样本，且前者可以看成后者的特殊形式；而 boosting 是针对残差样本．

第九章 加性模型、树模型及相关方法

这章中我们开始对监督学习中一些特定的方法进行讨论．这里每个技巧都假设了未知回归函数（不同的）结构形式，而且通过这样处理巧妙地解决了维数灾难．

当然，它们要为错误地确定模型类型付出可能的代价，所以在每种情形下都需要做出一个权衡．

第 3-6 章留下的问题都将继续讨论．我们描述 5 个相关的技巧：广义可加模型 (generalized additive models)，树 (trees)，多元自适应回归样条 (MARS)，耐心规则归纳法 (PRIM)，以及 混合层次专家 (HME)．

9.1 广义可加模型

在回归的设定中，广义可加模型有如下形式

\[ \text E(Y\mid X_1,X_2,\ldots,X_p) = \alpha+f_1(X_1)+f_2(X_2)+\cdots+f_p(X_p) \quad (9.1) \]

9.2 树模型

• 为什么二值分割？
  与其在每一步对每个结点只分割成两个群体（如上面讨论的），我们或许可以考虑多重分割成多于两个群体．尽管这个在某些情况下是有用的，但不是一个好的一般策略．问题在于多重分割将数据分得太快，以至于在下一层次没有充分多的数据．因此我们仅仅当需要的时候采用这种分割．因为多重分割可以通过一系列的二值分割实现，所以后者更好一点．
• 树的不稳定性
  树的一个主要问题是它们的高方差性．经常在数据中的一个小改动导致完全不同的分割点序列，使得解释不稳定．这种不稳定的主要原因是这个过程的层次性：上一个分割点的误差会传递到下面所有的分割点上．可以试图采取更加稳定的分离准则在某种程度上减轻这一影响，但是固有的不稳定性没有移除．这是从数据中估计一个简单的、基于树结构的代价．Bagging（8.7 节）对很多树进行平均来降低方差．
• 缺乏光滑性
  树的另一个限制是预测表面缺乏光滑性，如在图 9.2 中的右下图中那样．在 0/1 损失的分类问题中，这不会有太大的损伤，因为类别概率估计的偏差的影响有限．然而，在回归问题中这会降低效果，正常情况下我们期望潜在的函数是光滑的．(9.4 节)介绍的 MARS 过程可以看出是为了减轻 CART 缺乏光滑性而做的改动．

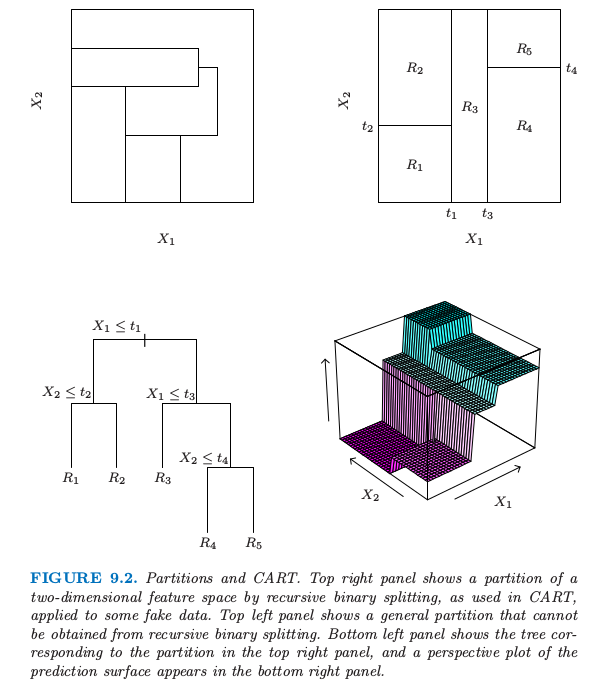
9.3 ROC

在医学分类问题中，敏感度 (sensitivity) 和 特异度 (specificity) 经常用来衡量一个准则．它们按如下定义：

• 敏感度：给定真实状态为患病预测为患病的概率
• 特异度：给定真实状态为未患病预测为未患病的概率

受试者工作特征曲线 ( receiver operating characteristic curve, ROC ) 是用于评估敏感度和特异度之间折中的常用概述．当我们改变分类规则的参数便会得到敏感度关于特异度的图像． 越靠近东北角落的曲线表示越好的分类器． ROC 曲线下的面积有时被称作 \(c\) 统计量 (c-statistics)．

9.4 专家的分层混合 (HME)

过程可以看成是基于树方法的变种．主要的差异是树的分割不是硬决定 (hard decision)，而是软概率的决定 (soft probabilistic)．在每个结点观测往左或者往右的概率取决于输入值．因为最后的参数优化问题是光滑的，所以有一些计算的优势，不像在基于树的方式中的离散分割点的搜索．软分割或许也可以帮助预测准确性，并且提供另外一种有用的数据描述方式．

第十章 提升方法与加性树模型

Boosting 是最近20年内提出的最有力的学习方法．最初是为了分类问题而设计的，但是我们将在这章中看到，它也可以很好地扩展到回归问题上．Boosting的动机是集合许多弱学习的结果来得到有用的“committee”．

弱分类器是误差率仅仅比随机猜测要好一点的分类器．Boosting 的目的是依次对反复修改的数据应用弱分类器算法，因此得到弱分类器序列: \[ G_m(x),m=1,2,\ldots,M \] 根据它们得到的预测再通过一个加权来得到最终的预测

事实上，Breiman(NIPS Workshop，1996) 将树的 AdaBoost 称为“世界上最好的现成分类器”(best off-the-shelf classifier in the world)． 有人认为决策树是 boosting 是数据挖掘应用中理想的基学习器．

10.1 数据挖掘的现货方法

个人注：“现货”(off-the-shelf) 方法．现货方法指的是可以直接应用到数据中而不需要大量时间进行数据预处理或者学习过程的精心调参．

预测学习 (predictive learning) 是数据挖掘中很重要的一部分．正如在这本书中看到的一样，已经提出了大量的方法对数据进行学习，然后预测．对于每个特定的方法，有些情形特别适用，但在其他情形表现得很差．我们已经试图在每个方法的讨论中明确合适的应用情形．然而，对于给定的问题，我们不会事先知道哪种方法表现得最好．表 10.1 总结了一些学习方法的特点．

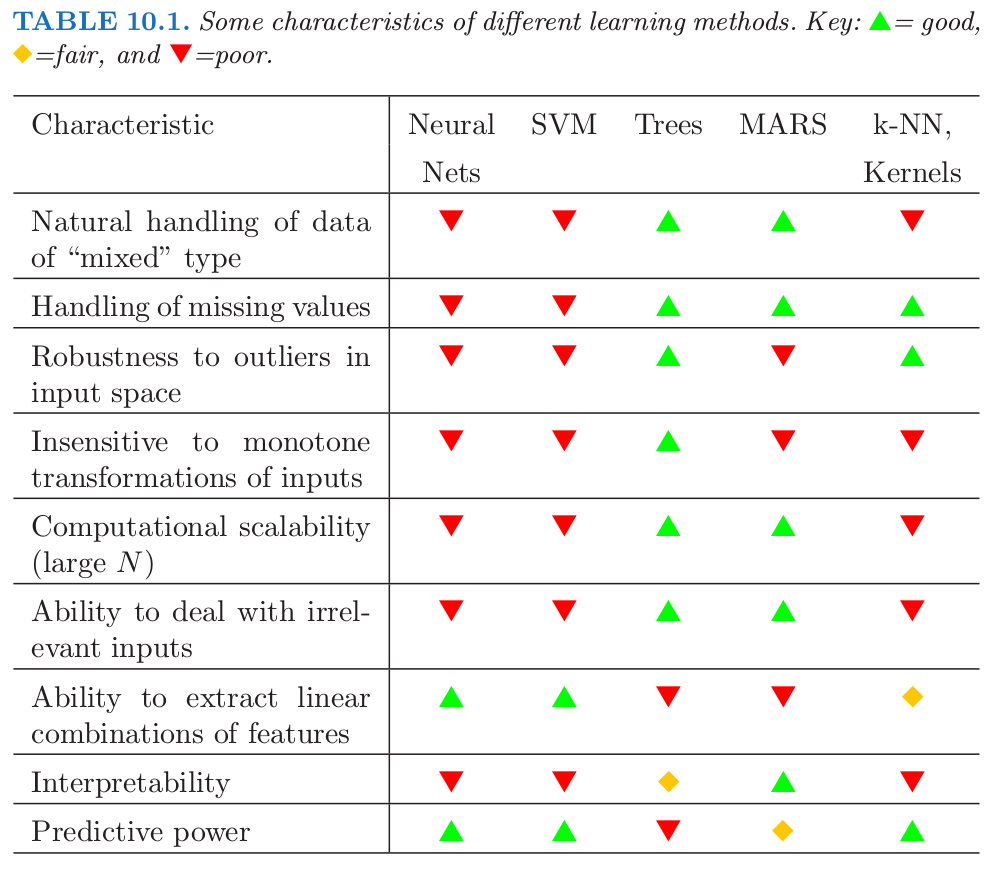
工业和商业数据挖掘应用在学习过程的要求往往特别具有挑战性．数据集中观测值的个数以及每个观测值上衡量的变量个数往往都非常大．因此，需要注意计算的复杂度．并且，数据经常是混乱的 (messy)：输入往往是定量，二值以及类别型变量的混合，而且类别型变量往往有很多层次．一般还会有许多缺失值，完整的观测值是很稀少的．预测变量和响应变量的分布经常是 长尾 (long-tailed) 并且 高偏的 (highly skewed)．垃圾邮件的数据就是这种情形(9.1.2 节)；当拟合一个广义可加模型，我们首先对每个预测变量进行对数变换以期得到合理的拟合．另外，它们通常会包含很大一部分的严重的误测量值（离群值）．预测变量通常在差异很大的尺度下进行测量．

在数据挖掘应用中，通常只有大量预测变量中的一小部分真正与预测值相关的变量才被包含在分析中．另外，不同于很多应用的是，比如模式识别，很少有可信的专业知识来创建相关的特征，或者过滤掉不相关的， 这些不相关的特征显著降低了很多方法的效果．

另外，数据挖掘一般需要可解释性的模型．简单地得到预测值是不够的．提供定性 (qualitative) 理解输入变量和预测的响应变量之间的关系的信息是迫切的．因此，黑箱方法(black box)，比如神经网络，在单纯的预测情形，比如模式识别中是很有用的，但在数据挖掘中不是很有用．

这些计算速度、可解释性的要求以及数据的混乱本性严重限制了许多学习过程作为数据挖掘的 “现货”(off-the-shelf) 方法．现货方法指的是可以直接应用到数据中而不需要大量时间进行数据预处理或者学习过程的精心调参．

在所有的有名的学习方法中，决策树最能达到数据挖掘的现货方法的要求．它们相对很快地构造出模型并且得到可解释的模型（如果树很小）．如 [9.2 节] 中讨论的，它们自然地包含数值型和类别型预测变量以及缺失值的混合．它们在对单个预测变量的（严格单调）的变换中保持不变．结果是，尺寸变换和（或）更一般的变换不是问题，并且它们不受预测变量中的离群值的影响．它们将中间的特征选择作为算法过程的一部分．从而它们抑制（如果不是完全不受影响）包含许多不相关预测变量． 决策树的这些性质在很大程度上是它们成为数据挖掘中最受欢迎的学习方法的原因．

树的不准确性导致其无法作为预测学习的最理想的工具．它们很少达到那个将数据训练得最好的方法的准确性．正如在 [10.1 节]看到的，boosting 决策树提高了它们的准确性，经常是显著提高．同时它保留着数据挖掘中所需要的性质．

一些树的优势被 boosting 牺牲的是计算速度、可解释性，以及对于 AdaBoost 而言，对重叠类的鲁棒性，特别是训练数据的误分类．gradient boosted model(GBM)是 tree boosting 的一般化，它试图减轻这些问题，以便为数据挖掘提供准确且有效的现货方法．

10.2 大小合适的boosting树

曾经，boosting 被认为是一种将模型结合起来(combing models)的技巧，在这里模型是树．同样地，生成树的算法可看成是产生用于 boosting 进行结合的模型的 原型(primitive)．这种情形下，在生成树的时候以通常的方式分别估计每棵树的最优大小（[9.2 节]）．首先诱导出非常大（过大的）的一棵树，接着应用自下而上的过程剪枝得到估计的最优终止结点个数的树．这种方式隐含地假设了每棵树是式 公式（10.28） 中的最后一棵．

Boosted 树模型是这些树的和:

\[ f_M(x)=\sum\limits_{m=1}^MT(x;\Theta_m)\tag{10.28}\label{10.28} \]

• 解释性
  单个决策树有着很高的解释性．整个模型可以用简单的二维图象（二叉树）完整地表示，其中二叉树也很容易可视化．树的线性组合 公式（10.28） 丢失了这条重要的特性，所以必须考虑用不同的方式来解释．
  
• 预测变量的相对重要性
  在数据挖掘应用中，输入的预测变量与响应变量的相关程度很少是相等的．通常只有一小部分会对响应变量有显著的影响，而绝大部分的变量是不相关的，并且可以简单地不用包含进模型．研究每个输入变量在预测响应变量时的相关重要度或者贡献是很有用的．

全书的读书笔记（共6篇）如下：
《统计学习基础》读书笔记之一
《统计学习基础》读书笔记之二
《统计学习基础》读书笔记之三
《统计学习基础》读书笔记之四
《统计学习基础》读书笔记之五
《统计学习基础》读书笔记之六