《统计学习基础》 (5/6)

第十一章：神经网络； 第十二章：支持向量机与灵活判别方法； 第十三章：原型方法与最近邻算法。

第十一章 神经网络

这章中我们描述一类学习方法，它是基于在不同的领域（统计和人工智能）中独立发展起来但本质上相同的模型．中心思想是提取输入的线性组合作为导出特征 (derived features)，然后将目标看成特征的非线性函数进行建模．这是一个很有效的学习方法，在许多领域都有广泛应用．我们首先讨论投影寻踪模型 (projection pursuit model)，这是在半参统计和光滑化领域中发展出来的．本章的剩余部分集中讨论神经网络模型．

11.1 投影寻踪回归

Projection Pursuit Regression

在我们一般监督学习问题中，假设我们有 \(p\) 个组分的输入向量 \(X\)，以及目标变量 \(Y\)．

令 \(\omega_m,m=1,2,\ldots, M\) 为未知参数的 \(p\) 维单位向量．投影寻踪回归 (PPR) 模型有如下形式: \[ f(X)=\sum\limits_{m=1}^Mg_m(\omega_m^TX)\tag{11.1}\label{11.1} \] 这是一个可加模型，但是是关于导出特征 \(V_m=\omega_m^TX\)，而不是关于输入变量本身．函数 \(g_m\) 未定，而是用一些灵活的光滑化方法来估计及 \(\omega_m\) 的方向（见下）．

函数 \(g_m(\omega_m^TX)\) 称为 \(\mathbb R^p\) 中的岭函数 (ridge function)．仅仅在由向量 \(\omega_m\) 定义的方向上变化．标量变量 \(V_m=\omega_m^TX\) 是 \(X\) 在单位向量 \(\omega_m\) 上的投影，寻找使得模型拟合好的 \(\omega_m\)，因此称为“投影寻踪”．图 11.1 显示了岭函数的一些例子。

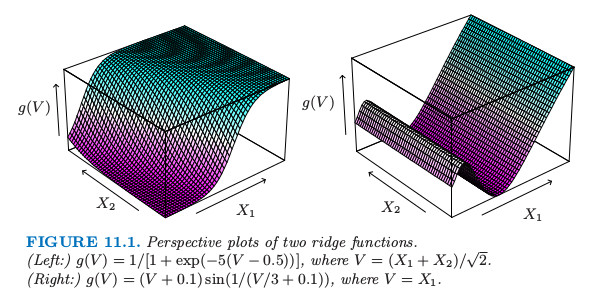
实际上，如果 \(M\) 任意大，选择合适的 \(g_m\)，PPR 模型可以很好地近似 \(\mathbb R^p\) 中任意的连续函数．这样的模型类别称为 通用近似 (universal approximator)．然而这种一般性需要付出代价．拟合模型的解释性通常很困难，因为每个输入变量都以复杂且多位面的方式进入模型中．结果使得 PPR 模型对于预测非常有用，但是对于产生一个可理解的模型不是很有用．\(M=1\) 模型是个例外，也是计量经济学中的 单指标模型 (single index model)．这比线性回归模型更加一般，也提供了一个类似（线性回归模型）的解释．

然而，投影寻踪回归模型在统计领域并没有被广泛地使用，或许是因为在它的提出时间（1981），计算上的需求超出大多数已有计算机的能力．但是它确实代表着重要的智力进步，它是一个在神经网络领域的转世中发展起来的

11.2 拟合神经网络

神经网络模型中未知的参数，通常称为 权重 (weights)，我们需要寻找它们的值使得模型很好地拟合训练数据．我们将参数的全集记为 \(\theta\)

对于回归，我们采用误差平方和用于衡量拟合的效果（误差函数） \[ R(\theta)=\sum\limits_{k=1}^K\sum\limits_{i=1}^N(y_{ik}-f_k(x_i))^2\tag{11.9} \]

对于分类，我们可以采用平方误差或者交叉熵（偏差）： \[ R(\theta)=-\sum\limits_{i=1}^N\sum\limits_{k=1}^Ky_{ik}\mathrm{log}\;f_k(x_i)\tag{11.10} \]

以及对应的分类器 \(G(x)=\mathrm{arg\; max}_kf_k(x)\)．有了 softmax 激活函数和交叉熵误差函数，神经网络模型实际上是关于隐藏层的线性逻辑斯蒂回归模型，而且所有的参数通过极大似然来估计．

一般地，我们不想要 \(R(\theta)\) 的全局最小值，因为这可能会是一个过拟合解．而是需要一些正则化：这个可以通过惩罚项来直接实现，或者提前终止来间接实现．下一节中将给出详细的细节．

最小化 \(R(\theta)\) 的一般方法是通过梯度下降，在这种情形下称作 向后传播 (back-propagation)．因为模型的组成成分，运用微分的链式法则可以很简单地得到梯度．这个可以通过对网络向前或向后遍历计算得到，仅跟踪每个单元的局部量．

向后传播的优点在于简单，局部自然．在向后传播算法中，每个隐藏层单元仅仅向（从）有其联系的单元传递（接收）信息．因此可以在并行架构的计算机上高效地实现．

批量学习 (batch learning)，参数更新为所有训练情形的和．学习也可以 online 地进行——每次处理一个观测，每个训练情形过后更新梯度，然后对训练情形重复多次．在这种情形下，公式（11.13） 式的和可以替换成单个被加数．一个 训练时期 (training epoch) 指的是一次扫描整个训练集．在线训练 (online training) 允许网络处理非常大的训练集，而且当新观测加入时更新权重．

另一方面，给定 \(g\)，我们想要关于 \(\omega\) 最小化 公式11.2．高斯-牛顿搜索可以很方便地实现这个任务．这是一个拟牛顿法，丢掉了 Hessian 阵中关于 \(g\) 二阶微分的项．可以很简单地按照下面导出．令 \(\omega_{old}\) 为 \(\omega\) 的当前估计．我们写成 \[ g(\omega^Tx_i)\approx g(\omega_{old}^Tx_i)+g'(\omega_{old}^Tx_i)(\omega-\omega_{old})^Tx_i\quad(11.3) \]

11.3 训练神经网络的一些问题

训练神经网络真的是一门艺术．模型一般会过参量化，而且优化问题非凸而且不稳定，除非遵循某确定的方式．在这节我们总结一些重要的问题．

• 初始值
  注意如果权重接近 0，则 sigmoid（图 11.3）起作用的部分近似线性，因此神经网络退化成近似线性模型（[练习 11.2]）．通常权重系数的初始值取为接近 0 的随机值．因此模型开始时近似线性，当系数增大时变成非线性．需要的时候局部化单个单元的方向并且引入非线性．恰巧为 0 的权重的使用导致 0 微分和完美的对称，而且算法将不会移动．而以较大的值开始经常带来不好的解． \(\sigma(sv)\) ，s是权重。

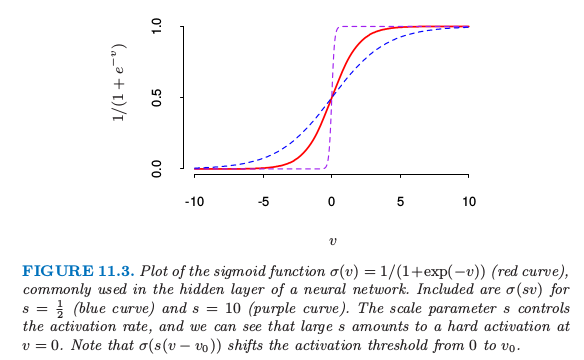
• 过拟合
  通常神经网络有太多的权重而且在 \(R\) 的全局最小处过拟合数据．在神经网络的发展早期，无论是设计还是意外，采用提前终止的规则来避免过拟合．也就是训练一会儿模型，在达到全局最小前终止．因为权重以高正则化（线性）解开始，这有将最终模型收缩成线性模型的效果．验证集对于决定什么时候停止是很有用的，因为我们期望此时验证误差开始增长． 一个更明显的正则化方法是 权重衰减 (weight decay)，类似用于线性模型的岭回归
• 输入的缩放
  因为对输入的缩放决定了在底层中系数缩放的效率，所有它可以对最终解有很大的影响．最开始最好是对所有输入进行标准化使均值为 0，标准差为 1．这保证了在正则化过程中对所有输入公平对待，而且允许为随机的初始权重系数选择一个有意义的区间．有了标准化的输入，一般在 \([-0.7,+0.7]\) 范围内均匀随机选择权重系数．
• 隐藏单元和层的个数
  一般来说，太多的隐藏单元比太少的隐藏单元要好．太少的隐藏单元，模型或许没有足够的灵活性来捕捉数据的非线性；太多的隐藏单元，如果使用了合适的正则化，额外的权重系数可以收缩到 0．一般地，隐藏单元的数量处于 5 到 100 的范围之内，而且随着输入个数、训练情形的种数的增加而增加．最常见的是放入相当大数量的单元并且进行正则化训练．一些研究者采用交叉验证来估计最优的数量，但是当交叉验证用来估计正则化系数这似乎是不必要的．隐藏层的选择由背景知识和经验来指导．每一层提取输入的特征用于回归或者分类．多重隐藏层的使用允许在不同的分解层次上构造层次特征．
• 多重最小点
  误差函数 \(R(\theta)\) 为非凸，具有许多局部最小点．后果是最终得到的解取决于权重系数的初始值．至少需要尝试一系列随机的初始配置，然后选择给出最低（惩罚）误差的解．或许更好的方式是在对一系列网络的预测值进行平均作为最终的预测．这比平均权重系数更好，因为模型的非线性表明平均的解会很差．另一种方式是通过 bagging，它是对不同网络的预测值进行平均，这些网络是对随机扰动版本的训练数据进行训练得到的．

第十二章 支持向量机与灵活判别方法

Lagrange 对偶函数 （公式12.13）有如下形式：

\[ L_D=\sum\limits_{i=1}^N\alpha_i-\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{i'=1}^N\alpha_i\alpha_{i'}y_iy_{i'}\langle h(x_i), h(x_{i'})\rangle\label{12.19}\quad(12.19) \]

从 公式（12.10） 中我们看到解函数 \(f(x)\) 可以写成

\[ \begin{align} f(x)&=h(x)^T\beta+\beta_0\notag\\ &=\sum\limits_{i=1}^N\alpha_iy_i\langle h(x),h(x_i) \rangle+\beta_0\label{12.20}\tag{12.20} \end{align} \]

所以 公式（12.19） 和 公式（12.20） 仅仅通过内积涉及 \(h(x)\)．实际上，我们根本不需要明确变换关系 \(h(x)\)，而仅仅要求知道在转换后的空间中计算内积的核函数 \[ K(x,x')=\langle h(x), h(x') \rangle\tag{12.21} \]

在 SVM 中有三种流行的 \(K\) 可以选择

\[ \begin{array}{rl} d\text{ 阶多项式：} & K(x,x')=(1+\langle x,x' \rangle)^d\\ \text{径向基：} & K(x, x')=\exp(-\gamma \Vert x-x'\Vert^2)\quad(12.22)\\ \text{神经网络：} & K(x,x')=\tanh(\kappa_1\langle x,x' \rangle+\kappa_2)\\ \end{array} \]

考虑含有两个输入变量 \(X_1\) 和 \(X_2\) 的特征空间，以及 2 阶的多项式核．则

\[ \begin{array}{ll} K(x,x')&=(1+\langle X,X' \rangle)^2\\ &=(1+X_1X_1'+X_2X_2')^2\\ &=1+2X_1X_1'+2X_2X_2'+(X_1X_1')^2+(X_2X_2')^2+2X_1X_1'X_2X_2'\quad(12.23) \end{array} \]

则 \(M=6\)，而且如果我们选择 \[ h_1(X)=1,h_2(X)=\sqrt{2}X_1,h_3(X)=\sqrt{2}X_2,h_4(X)=X_1^2,h_5(X)=X_2^2 \] 以及 \[ h_6(X)=\sqrt{2}X_1X_2 \] 则

\[ K(X,X')=\langle h(X),h(X')\rangle \]

第十三章 原型方法与最近邻算法

不变量和切线距离 对于每张图像，我们画出了该图像旋转版本的曲线，称为 不变流形 (invariance manifolds)．现在，不是用传统的欧氏距离，而是采用两条曲线间的最短距离．换句话说，两张图像间的距离取为第一张图像的任意旋转版本与第二张图像的任意旋转版本间的最短欧氏距离．这个距离称为 不变度量 (invariant metric)．

原则上，可以采用这种不变度量来进行 1 最近邻分类．然而这里有两个问题．第一，对于真实图像很难进行计算．第二，允许大的变换，可能效果很差．举个例子，经过 180° 旋转后，“6” 可能看成是 “9”．我们需要限制为微小旋转．

切线距离 (tangent distance) 解决了这两个问题．如图 13.10 所示，我们可以用图像“3”在其原图像的切线来近似不变流形．这个切线可以通过从图像的微小旋转中来估计方向向量，或者通过更复杂的空间光滑方法（[练习 13.4]）．对于较大的旋转，切线图像不再像“3”，所以大程度的旋转问题可以减轻．

想法是对每个训练图像计算不变切线．对于待分类的 查询图像 (query image)，计算其不变切线，并且在训练集的直线中寻找最近的直线．对应最近的直线的类别（数字）是对查询图像类别的预测值．在图 13.11 中，两条切向直线相交，但也只是因为我们是在二维空间中表示 256 维的情形．在 \(\mathbb R^{256}\) 中，两条这样的直线相交的概率是 0．

自适应最近邻方法： 最近邻分类的隐含假设是类别概率在邻域内近似为常值，因此简单的平均会得到不错的估计．然而，在这个例子中，只有水平方向上的类别概率会变化．如果我们提前知道这一点，可以将邻居拉伸为长方形区域．这会降低估计的偏差，同时保持方差不变．

一般地，这要求最近邻分类中采用自适应的度量，使得得到的邻域沿着类别不会改变太多的方向上拉伸．在高维特征空间中，类别概率可能仅仅只在一个低维的子空间中有所改变，因此自适应度量是很重要的优点．

判别自适应最近邻 (DANN) 方法进行了局部维度降低——也就是，在每个查询点单独降低维度．提出通过逐步剔除包含训练数据的盒子的边来自动寻找长方形邻域．这里我们介绍 Hastie and Tibshirani (1996a)提出的 判别自适应最近邻 (discriminant adaptive nearest-neighbor) (DANN)．在每个查询点，构造其大小为 50 个点的邻域，并且用这些点的类别分布来决定怎么对邻域进行变形——也就是，对度量进行更新．接着更新后的度量用在该查询点的最近邻规则中．因此每一个查询点都可能采用不同的度量．很明显邻域应当沿着垂直类别重心连线的方向拉伸．这个方向也与线性判别边界重合，而且是类别概率改变最少的方向．一般地，类别概率变化最大的方向不会与类别重心连线垂直

计算上的考虑：最近邻分类规则的一个缺点通常是它的计算负荷量，无论是寻找最近邻还是存储整个训练集合．

全书的读书笔记（共6篇）如下：
《统计学习基础》读书笔记之一
《统计学习基础》读书笔记之二
《统计学习基础》读书笔记之三
《统计学习基础》读书笔记之四
《统计学习基础》读书笔记之五
《统计学习基础》读书笔记之六