金融时间序列相关分析模型资料
相关概念
- 协方差、自相关、偏相关、时间序列建模、时间序列预测、ARIMA、P值、t检验、贝叶斯公式、条件概率。
- 风险=波动=方差=离散度
几个概念定义
https://blog.csdn.net/Yuting_Sunshine/article/details/95317735
时间序列
每个时间序列数据集都可以分解为其组成部分,即趋势、季节性和残差。
- 时间序列的正式定义如下:它是一系列在相同时间间隔内测量到的数据点。
- 该序列中的每个数据点都与先前的数据点相关。 (所以可以用来预测)
自相关函数 (ACF)
延迟为 k 时,这是相距 k 个时间间隔的序列值之间的相关性。
偏自相关函数 (PACF)。延迟为 k 时,这是相距 k
个时间间隔的序列值之间的相关性,同时考虑了间隔之间的值。
偏自相关函数(PACF)
偏自相关函数用来度量暂时调整所有其他较短滞后的项 (y_{t-1}, y_{t-2},
…, y_{t-k-1}) 之后,时间序列中以 k
个时间单位(y_{t}和y_{t-k})分隔的观测值之间的相关。
类似游泳和冷饮销售, (y_{t-1}, y_{t-2}, …, y_{t-k-1})
就类似增加气温及其它控制参数(这里是K-1个参数)
偏自相关是剔除干扰后时间序列观察与先前时间步长时间序列观察之间关系的总结。在滞后k处的偏自相关是在消除由于较短滞后条件导致的任何相关性的影响之后产生的相关性。一项观察的自相关和在先验时间步上的观测包括直接相关和间接相关。这些间接相关是线性函数观察(这个观察在两个时间步长之间)的相关。偏自相关函数试图移除这些间接相关。
置信度的概念
置信度就是说,你测得的均值,和总体真实情况的差距小于这个给定的值的概率,应该是1-α,如式(4),换句话说,我们有1-α的信心认为,你测得的这个均值和总体的实际期望很接近了。(说你测得的均值就是总体期望是很草率的,但是说,我有95%的把握认为我测得的均值,非常接近总体的期望了,听起来就靠谱的多)
https://zhuanlan.zhihu.com/p/609446579 (置信区间的技术文档)
T分布
T检验、T分布、T检验的计算方法
https://zhuanlan.zhihu.com/p/86188571 (很好的一篇关于T检验的文章)
T分布的特点
(1)t分布为对称分布,关于t=0对称,只有一个峰,峰值在t=0处,与标准正太分布曲线相比,t分布曲线顶部略底,两尾部稍高而平。
(2)t分布曲线受自由度影响,自由度越小,离散程度越大。
(3)t分布的极限是正太分布,自由度越大,越接近标准正太分布。
(4)当n>30时,t分布与标准正太分布的区别较小;当n>100时,t分布与标准正太分布基本一致;n接近无穷时,t分布与标准正太分布完全一致。
(5)t分布适用于n小于30的场景。
贝叶斯公式
联合概率、条件概率、独立性、后验概率、样本空间
条件概率与联合概率:
https://yangzhe.me/2018/10/26/conditional_and_joint_probability/
全概公式与贝叶斯公式(通俗易懂、新角度讲解)
https://zhuanlan.zhihu.com/p/636852568
为什么从定义上看,觉得联合概率和条件概率是一个意思?
https://www.zhihu.com/question/278117164/answer/400273059
三门问题
贝叶斯解三门问题:
https://zhuanlan.zhihu.com/p/692929293
问题描述
假设你在参加一个电视节目,节目里面有三扇门,其中只有1扇门中有一辆小汽车作为选中的礼物,选中有小汽车的门奖品就归你,你作为嘉宾,主持人在刚开始先让你选择了一扇门A,在第二个环节又帮你排除了剩下的两扇门B,C中的一扇空门B,最后选择权到你手中,问你是否愿意用已选择的门A交换剩下的门C?到底哪个门后有小汽车的概率更大?问题求解
此问题属于典型的贝叶斯条件概率问题
正确答案是,在发生事件D,排除一扇空门后,P(A|D)=1/3,而剩下的那扇门的概率P(C|D)=2/3
建模过程如下:
假设事件A,B, C分别表示门A, B, C后有小汽车,则初始状态P(A)=P(B)=P(C)=1/3
事件D,表示主持人排除第二扇门B,则利用全概率公式P(D)=P(D|A)P(A) + P(D|B)P(B) + P(D|C)P(C)
P(D|A)表示小汽车在门A后面,门B被打开的概率,主持人从B,C中随机取一扇即可,P(D|A)=1/2
P(D|B)表示小汽车在B后面,门B被打开的概率,P(D|B)=0,
P(D|C)表示小汽车在C后面,门B被打开的概率,P(D|C)=1
所以P(D)=(1/2)*(1/3) + (1/3)=1/2
最终实际上要计算的概率是,
P(A|D)= P(D|A)P(A)/P(D)=(1/2) * (1/3) /(1/2)=1/3
P(C|D)=P(D|C)P(C)/P(D)=1 * (1/3)/(1/2)=2/3
投资的目的
投资组合是为了分散风险,在一定的收益下,风险的最小化;或者在一定的风险下收益最大化。
投资不是最求收益最大化,所以需要考虑风险对冲。
风险价值模型(VaR)
Value at risk
模型的关键
- 假设;
- 模型的核心是输入输出(Input、Output);
- 预测,很多时候先人工判断(借助计算机工具和图形),选取在不同的参数下的得分;也可以让机器按不同的参数做预测,然后比较预测结果,选择相关的最优参数;
七种时间序列预测方法
https://www.modb.pro/db/219387
在拿到数据集的时候,根据经验做初步的判断,然后使用合适的方法也是一种经验!在过程中,如果模拟的分数不高,可以尝试不同的方法,直到找到合适的方法为止。
从这些步骤中可以学到的一个教训是,这些模型中的每一个都可以在特定数据集上优于其他模型。因此,这并不意味着在一种类型的数据集上表现最佳的模型对于所有其他数据集也表现相同。
ARIMA模型
自回归综合移动平均(Auto-Regressive Integrated Moving
Averages)的首字母缩写。
ARIMA模型建立在以下假设的基础上:
- 数据序列是平稳的,这意味着均值和方差不应随时间而变化。通过对数变换或差分可以使序列平稳。
- 输入的数据必须是单变量序列,因为ARIMA利用过去的数值预测未来的数值。
ARIMA模型(差分整合移动平均自回归模型)
https://www.modb.pro/db/219387
虽然ARIMA是一个非常强大的预测时间序列数据的模型,但是数据准备和参数调整过程是非常耗时的。在实现ARIMA之前,需要使数据保持平稳,并使用前面讨论的ACF和PACF图确定p和q的值。AutoARIMA让整个任务实现起来非常简单
实现ARIMA模型的通用步骤如下:(个人注:应该是大部分建模的通用流程)
- 加载数据:构建模型的第一步当然是加载数据集。
- 预处理:根据数据集定义预处理步骤。包括创建时间戳、日期/时间列转换为d类型、序列单变量化等。
- 序列平稳化:为了满足假设,应确保序列平稳。这包括检查序列的平稳性和执行所需的转换。
- 确定d值:为了使序列平稳,执行差分操作的次数将确定为d值。
- 创建ACF和PACF图:这是ARIMA实现中最重要的一步。用ACF PACF图来确定ARIMA模型的输入参数。
- 确定p值和q值:从上一步的ACF和PACF图中读取p和q的值。
- 拟合ARIMA模型:利用我们从前面步骤中计算出来的数据和参数值,拟合ARIMA模型。
- 在验证集上进行预测:预测未来的值。
- 计算RMSE:通过检查RMSE值来检查模型的性能,用验证集上的预测值和实际值检查RMSE值。
虽然ARIMA是一个非常强大的预测时间序列数据的模型,但是数据准备和参数调整过程是非常耗时的。在实现ARIMA之前,需要使数据保持平稳,并使用前面讨论的ACF和PACF图确定p和q的值。Auto ARIMA让整个任务实现起来非常简单,因为它去除了我们在上一节中提到的步骤3至6。
下面是实现AUTO ARIMA应该遵循的步骤:(个人注:简化后理论上说应该是有些地方要注意的,或者说是不是有条件的?)
- 加载数据:此步骤与ARIMA实现步骤1相同。将数据加载到笔记本中。
- 预处理数据:输入应该是单变量,因此删除其他列。
- 拟合Auto ARIMA:在单变量序列上拟合模型。
- 在验证集上进行预测:对验证集进行预测。
- 计算RMSE:用验证集上的预测值和实际值检查RMSE值。
VaR风险测度
https://zhuanlan.zhihu.com/p/111692540 (VaR概念性介绍)
VaR风险模型:
在金融数据的分析中,很多情况下我们会假设数据满足正态分布,例如证券的收益率和价差等。
在一些量化交易策略中,正态分布也为我们提供了许多便捷,例如很多配对交易策略,就是以证券对之间的价差变化服从正态分布为假设前提的。
有了这个分布,我们就方便了。如果要计算在95%的概率下,损失不会超过多少,我们只要计算在5%的概率下,损失是多少,就能知道损失不超过多少了。
当然,正态分布只是一个我们能假定的最简单的分布,在实际中,很多资产的收益率是不符合正态分布的,可能是其他分布,也可能是完全没有分布。
如果是其他分布,找到这种分布,采用一样的方法即可。
如果没有分布,那就用历史模拟法,也是可以得出结论的。
2008年金融危机爆发之前,华尔街的许多风险管理模型都非常精确,VaR的概念让这些公司得以在不同情况下可能损失的资产进行量化,但问题是,嵌入这些模型中有关全球市场可能会发生的风险假设其实是错误的,因而精确计算所得出的结论从根本上说就是不准确的。
https://wiki.mbalib.com/zh-tw/VaR%E6%96%B9%E6%B3%95 (概念性介绍)
https://zhuanlan.zhihu.com/p/669170449 (VaR具体的算法介绍)
有几种计算VaR的方法,每种方法都有自己的假设和局限性。在本文中,我们将探讨三种常用的VaR计算方法:历史模拟法、参数化法、蒙特卡洛模拟法
需要注意的是:VAR并不提供关于损失超过这个值的情况下可能面临的实际损失的信息。因此,在使用VAR时还需要结合其他风险度量指标和情景分析,来更全面地了解潜在风险。
知乎上有人将VaR模型视为史上最蠢的指标(见
https://www.zhihu.com/question/21774616/answer/19739484 )
在此我不敢苟同,在我看来这是因为大家对VaR的期望太高,很多人对VaR不满意的地方主要在于两点.
一是建模准确性问题,历史模拟法计算VaR太过依赖尾部数据,参数法下的正态分布假设不准确,因为几乎不存在刚好符合正态分布的金融时间序列,且大部分序列都是厚尾的,因此低估了尾部风险,这些的确都是VaR模型的缺点.但是大家都知道,所有建模都是错误的,但是有些模型是有用的,建模就是离不开假设。VaR模型普遍作为一种市场风险度量指标,和金融衍生品定价不同,其精确度的不足完全可以忍受,而衍生品定价则对准确度要求要高许多,却在风险中性定价原理中(如Black-Scholes期权定价模型),同样作了正态分布的假设。
对VaR模型的第二点不满意的地方在于其对极端损失的度量不足,这就是典型的期望过高,因为VaR度量的是市场正常波动下的极端损失,VaR只是一把杀猪刀,不是屠龙刀,但是没人说杀猪刀最蠢最没用,因为杀猪刀本来就只能杀猪,不能屠龙,你想让杀猪刀有屠龙刀的功能,就只能说杀猪刀没用了。
杀猪刀的升级版就是压力测试,以及预期损失模型(ES模型),ES模型度量的是组合超过VaR值的平均损失,的确更能反映尾部风险,但是它不易于理解,ES模型度量的是尾部平均损失,但是其波动范围多大?模型没有提供解释,另一方面,ES模型无法验证其有效性,因此总的说来在实用性上ES模型并不如VaR模型。而未来真的会有人研究出屠龙刀吗?恐怕很难,在金融危机等极端情形下,整个金融系统的系统性风险很容易将自己击溃,而这种极端事件的发生可能性微乎其微,所以我们在日常经营中无需时常采取准备措施预防这种系统性风险,不然只会造成资本资源的浪费。
因此,不管是VaR模型,还是其他风险计量指标,都只是风险管理的一方面,它们始终代替不了经验、判断,在面临可能到来的系统性风险等极端情形时,经验和判断可以让我们提前消除风险,这才是最有效的风险管理。
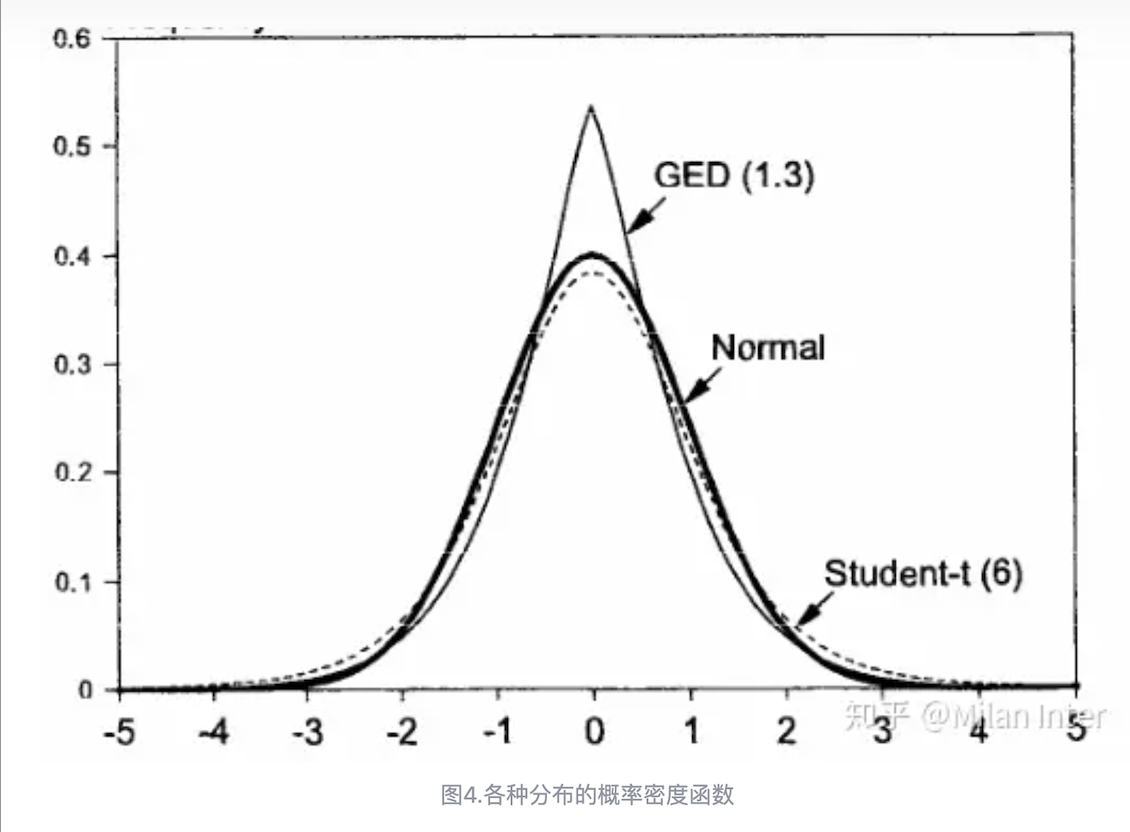
正态分布由于其计算的方便性已经被广泛应用于金融时间序列分析,虽然它不是拟合金融时间序列的最佳分布。金融时间序列常表现出尖峰厚尾性,因此实务中也会对金融序列做其他分布假设,最常用的有t分布以及广义误差分布(GED分布)。t分布的分布函数有一个自由度参数 𝑛 , 𝑛越小则分布的厚尾性越好,而当 𝑛越大时,t分布就趋近于正态分布。广义误差分布与t分布类似,也能更好的拟合尖峰厚尾特征,正态分布就是广义误差分布的一种特殊情况。
关于 VaR 的争议,一直都存在。
不少投资界的大腕批评过 VaR 的使用,Charlie Munger 算是他们中最著名的的一位。其他的专门撰写长文的包括著名的 Trader 和风险研究专家 Nassim Taleb(对,就是那个写了一本叫做 Black Swan 的书的作者)和 David Einhorn(这位做投资的都知道吧)
David 在 GARP 的杂志(就是那个发 FRM 牌子的组织的杂志)上发了一篇长文,写他是如何看空美国银行业的,
其中对 VaR 的批评很到位(果然,好的投资者都是优秀的风控经理):
- 风控经理的职责是关注那些很少发生但是影响重大的风险,而不是常规损失。VaR 在设计上,把尾部风险直接砍掉了,也就是说,VaR 能够回答你 95% 或 99% 的情况下,你的最大能损失是 XX 百万美元,但是不能回答你,在那 1% 或 5% 的情况下(装一点的话,就是 black swan event 发生的情况下)你的最大损失是多少,在极端情况下,你的损失最小是 VaR 所统计的数,最大,不知道,也许是一个天文数字。用统计的术语说,就是让风控经理把注意力集中在那些处在分布接近中央的可以管理的常规风险,而忽略了尾部风险。
- 由于 VaR 不能很好地度量尾部风险,所以在那些用 VaR 去衡量风险并找交易员的银行里面,交易员会有意规避这个监管指标(game the system),去投资那些风险非常低但是一旦风险失去大的投资机会(take excessive but remote risks),这也是为什么大银行会出现大的 trading loss 的原因之一。这里有一个小例子,就是开一个特别扭的赌局,概率是 1:127,赌硬币不可能次次都扭正面。从概率上说,这个赌很安全,出现金了 7 次正面概率只有 1/128,约等于 0.78%。也就是说,在 99% 的情况下,这个赌是赚钱的,这个投资机会的 VaR 值是 0。因为在 99% 的情况下你是赚钱的,但是你输一次,你亏损是你平时赚的 127 倍,通常的金融机构都有很高的杠杆,出现一次,就破产了。
- 第三个重要的问题,就是 VaR 是给高管汇报和监管层看的,监管者通常不是专门的风险专家,他们没有对 VaR 的深刻理解,容易让高管和监管层低估风险(have a false sense of security)。在美国 SEC 经常被认为 toothless 的监管机构,就是因为在大投行的监管上,SEC 一再让步。VaR 值作为 SEC 认可的风险监管披露方式,不出意外是投行游说的结果。按照 SEC 2004 年通过的条例,大投行可以选择用自己的一套方法去管理风险,只要他们愿意向 SEC 做更多披露,SEC 并不具备审查投行日益复杂的资产负债表的能力,所以,基本上就是你报一个 VaR 我就认为你没问题了。在中国,大家都知道,报数会有水分的。在美国也一样。
对于尾部风险,一个非常好的注脚是:人性不能用正态分布模型解释。在面对风险的时候,天生本性和后天教育教导我们,需要避险!一个著名的交易员法则是,不要抄底,十抄九死。(美国人也有类似说法,don't catch a falling knife.)所以,在风险来临的时候,大家会一窝蜂冲向出口,在市场狂热的时候,大家会羊群一样跟进。装一点的话,这叫反身性。人性决定了尾部风险高于正态分布预测的那么低。所以,用正态分布算出来的 VaR 会低估风险。Taleb 为了尾部风险写了整整一本书,有空大家看看吧。
注意⚠️
与数据分析不同,在真实的证券交易中,对各位投资人来说至关重要的是买入/卖出时机(量化中的买入/卖出信号)的把握,而非文中为进行数据分析而考虑的误差。
使用预测模型得到的信息只具有参考意义,理论上不存在100%成功率的预测方法,还请各位谨记投资有风险,入市需谨慎,操作不注意,亲人两行泪。