黄金分割

黄金比例，又称黄金分割，是一个数学常数，一般以希腊字母 \(\phi\) 表示。可以透过以下代数式定义：
\[\dfrac {a+b} {a}=\dfrac {a} {b}=\phi \qquad \left(a>b>0\right)\]
这也是黄金比例一名的由来。
黄金比例的准确值为 \(\dfrac {1+\sqrt {5}} {2}\) ，所以是无理数，而大约值则为（小数点后20位）：
\[\phi=1.61803398874989484820\]
应用时一般取1.618，就像圆周率在应用时取3.14一样。
黄金分割具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值，而且呈现于不少动物和植物的外观。现今很多工业产品、电子产品、建筑物或艺术品均普遍应用黄金分割，展现其功能性与美观性。

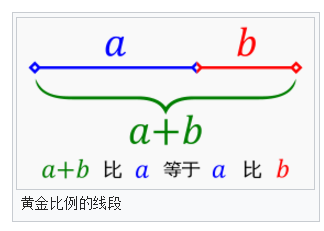
一个得出 \(\phi\) 数值的方法是从左边的分数式入手。经过简化和代入，
\[\dfrac {a+b} {a}=1+\dfrac {b} {a}=1+\dfrac {1} {\phi}\]

于是：
\[1+\dfrac {1}{\phi }=\phi\]
两边乘以\(\phi\) 就得到：
\[\phi +1=\phi ^{2}\]
即是 \(\phi^{2}-\phi -1=0\)
找出该方程的正解，
\[\phi =\dfrac {1+\sqrt {5}}{2}=1.6180339887\]
黄金分割奇妙之处，在于其倒数为自身减1，即：1.618...的倒数为0.618... = 1.618... - 1，并时常被称为“黄金比例共轭”。
从上面的\(1+\dfrac {1}{\phi }=\phi\) 得到：
\[\dfrac {1} {\phi }=\phi -1\]
这个0.618...的数值常用希腊字母 \(\Phi\) 表示，即：
\[\Phi =\dfrac {1} {\phi } =\dfrac{1} {1.6180339887...} =0.6180339887...\]
亦可表达为：
\[\Phi =\phi -1=1.6180339887... -1=0.6180339887...\]