《数学桥--对高等数学的一次观赏之旅》读书心得之四
接上篇:《数学桥--对高等数学的一次观赏之旅》读书心得之三
四、微积分与微分方程
1、微积分
积分的本质就是无限细分然后求和!
具体的求导、积分的公式见前文二、分析中对应微分和积分的部分!
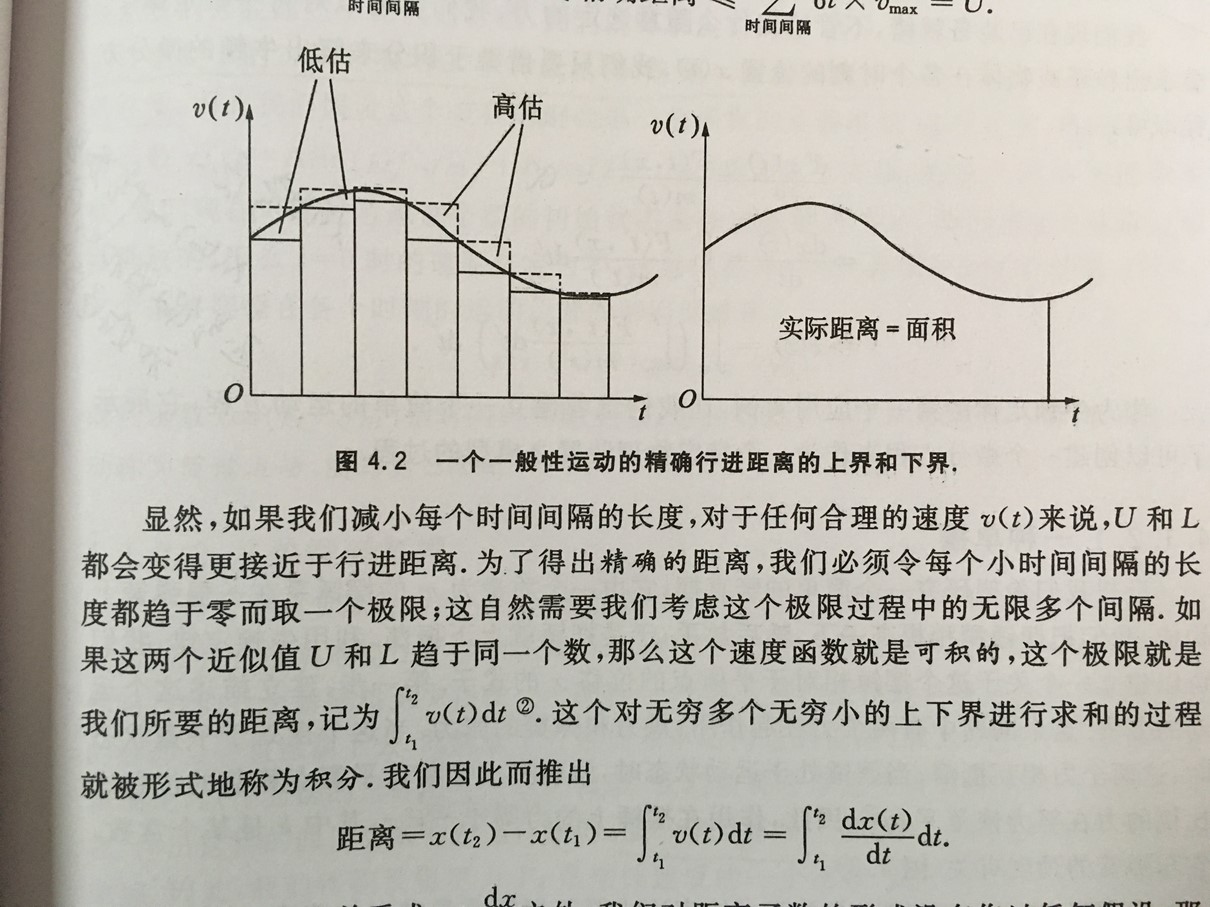
微积分基本定理:积分和求导是一对互逆的过程。

2、线性常微分方程
通常用像t,exp(t),sin(x),cos(x),lnt这些常见函数的组合来猜测微分方程解的可能形式,尽管有时候借着几分运气!
1) 解齐次线性方程
- 猜测法
我们研究一些方法,这些方法让我们对一个完全非线性系统其实根本不需要去求得任何解就能得到关于这些解的有效信息!这些定性的方法是微分方程中混沌现象研究的基础!
- 幂级数法
我们将要利用的事实是,如果一个函数在点t=0处的各阶导数形态良好,那么正如我们学习分析学时所知道的,它就是一个关于原点的幂级数展开式,先把一个微分方程化成一个关于幂级数的方程,这个方程就有可能解出。
化成幂级数之后,先代入方程,通过满足方程的解,求出幂级数的系数!
有些方程需要用到广义的幂级数来展开,例如贝塞尔函数。
2)解非齐次方程
解是非线性系统。例如:f(x+y)!=f(x+y)
求出一个特解,然后再求出对应齐次方程的一个解,然后加起来,就得出另外一个特解。
个人理解:线性方程和线性系统是不一样的,线性方程代表,未知数没有幂次项;而线性系统,指方程的解满足线性系统要求,就是不同解的线性组合还是方程的解。例如齐次方程和非齐次方程可以都是线性方程,但是齐次方程的解是线性系统;而非齐次方程的解不是线性系统!
3、偏微分方程
f(x,t),偏袒一方的求f(x,t)关于x和t的导数,偏导数可以看做函数f(x,t)在另一个变量的值固定时的变化率。要对函数求偏导数,你只要暂时把另外一个变量看成常数,像一维情况那样求导数就行了。
当要建立一个微分方程时,我们首先探究这个问题的一个离散化近似,然后取极限以确定精确解!
物理或化学方程为什么往往是偏微分方程?因为这些运动或者变化,并且都会受多个变量的影响,例如,运动会随时间或者位置而变化,所以在实际过程当中,就先离散化,然后求极限来处理,所以基本都是用偏微分方程来表示
1)弦振动方程
弦振动方程

波动方程
\[{\partial ^{2}u(x,t) \over \partial
t^{2}}={KL^{2} \over M}{\partial ^{2}u(x,t) \over \partial
x^{2}}\]
在这个例子中,波速\[{\displaystyle c={\sqrt
{\frac {KL^{2}}{M}}}} \]
一般解
代数方法
一维标量形式波动方程的一般解是由达朗贝尔给出的。原方程可以写成如下的算子作用形式:
\[{\displaystyle \left[{\frac {\partial
}{\partial t}}-c{\frac {\partial }{\partial x}}\right]\left[{\frac
{\partial }{\partial t}}+c{\frac {\partial }{\partial x}}\right]u=0.\,}
\]
从上面的形式可以看出,若F和G为任意函数,那么它们以下形式的组合
\[{\displaystyle
u(x,t)=F(x-ct)+G(x+ct)\,}\]
必然满足原方程。上面两项分别对应两列行波("行"与"行动"中同音)——F表示经过该点(x点)的右行波,G表示经过该点的左行波。为完全确定F和G的最终形式还需考虑如下初始条件:
\[{\displaystyle u(x,0)=f(x)\,} \]
\[{\displaystyle u_{t}(x,0)=g(x)\,} \]
经带入运算,就得到了波动方程著名的达朗贝尔行波解,又称达朗贝尔公式:
\[{\displaystyle u(x,t)={\frac
{f(x-ct)+f(x+ct)}{2}}+{\frac {1}{2c}}\int _{x-ct}^{x+ct}g(s)ds}
\]
在经典的意义下,如果 \({\displaystyle f(x)\in
C^{k}}\) 并且 \({\displaystyle g(x)\in
C^{k-1}}\) 则 \({\displaystyle
u(t,x)\in
C^{k}}\)。但是,行波函数F和G也可以是广义函数,比如狄拉克δ函数。在这种情况下,行波解应被视作左行或右行的一个脉冲。
基本波动方程是一个线性微分方程,也就是说同时受到两列波作用的点的振幅就是两列波振幅的相加。这意味着可以通过把一列波分解成它的许求解中很有效。此外,可以通过将波分离出各个分量来分析,例如傅里叶变换可以把波分解成正弦分量。
弦乐器

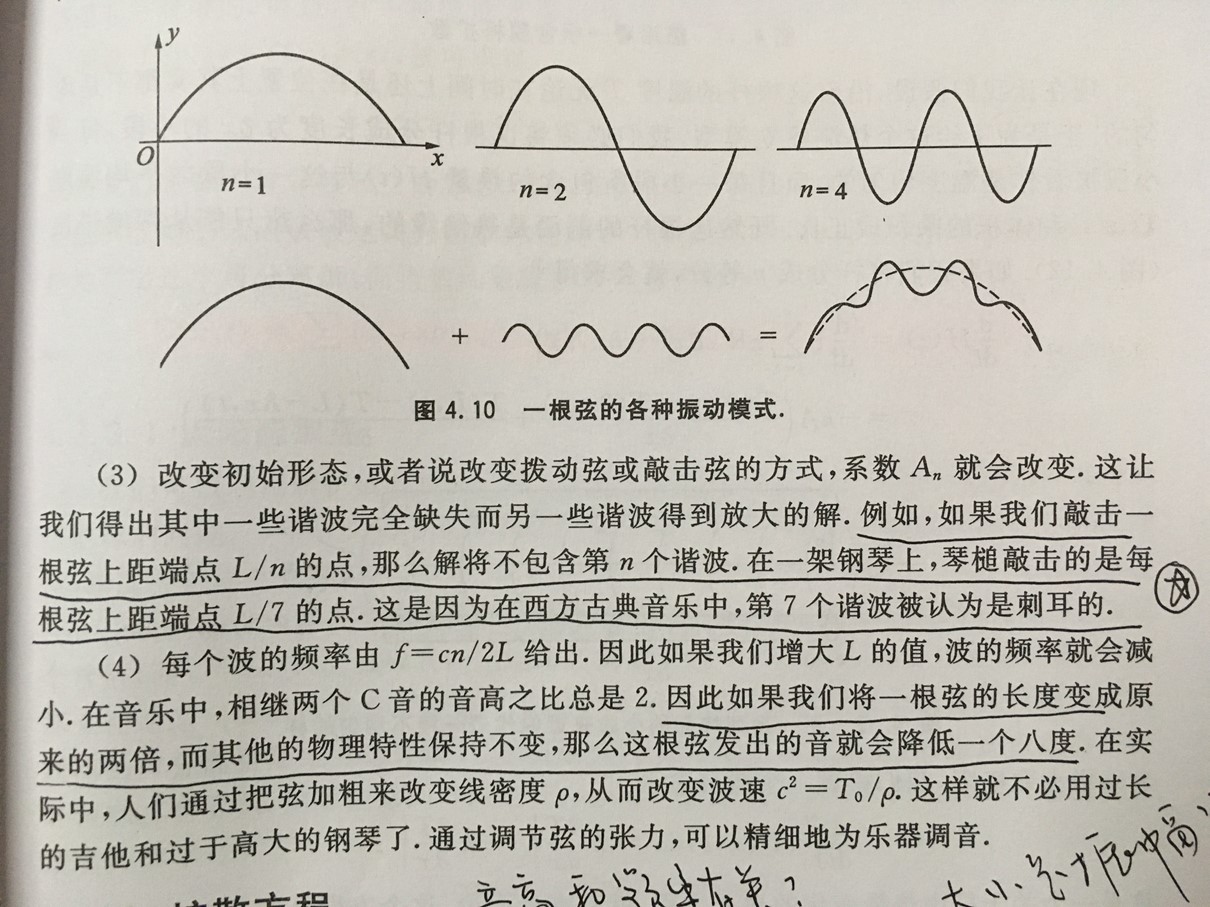
2)扩散方程

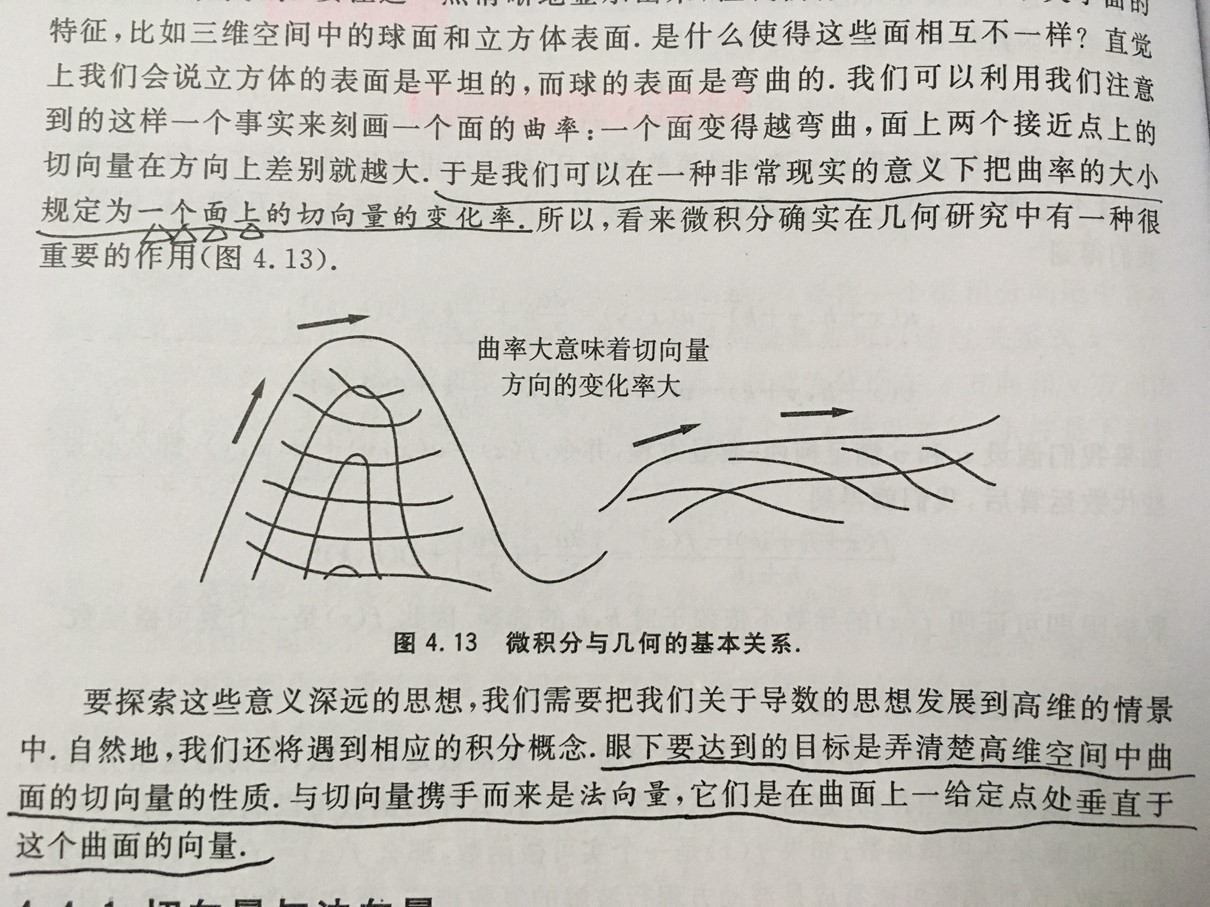
4、微积分与几何相遇
1) 切向量和法向量

2) 梯度、散度和旋度
下一篇:《数学桥--对高等数学的一次观赏之旅》读书心得之五