《数学桥--对高等数学的一次观赏之旅》读书心得之三
接上篇:《数学桥--对高等数学的一次观赏之旅》读书心得之二
三、代数
1、线性方程
2、向量及向量空间
一个向量空间完全由它的维数和用来与向量做标量乘法的数系所刻画。
3、矩阵
矩阵用来表示向量函数。
4、非齐次线性方程
解线性方程的本质实际上就是求矩阵的逆阵!
矩阵A可逆的充要条件是A中列向量的任何一个线性组合都不为0;例如:不能一列全是0,或者两列完全相同!反过来,矩阵任何一个列向量线性组合都不可能等于零最明显的情况是这个矩阵是单位矩阵的一个纯量倍数。
5、行列式
行列式:detA表示A的行列式;一个方阵A有一个逆阵的充要条件是detA!=0。
对于简单的2阶和3阶的矩阵,行列式的表达式相对简单,而且恰好是每条主对角线(左上至右下)元素乘积之和减去每条副对角线(右上至左下)元素乘积之和(见图中红线和蓝线)。
2阶矩阵的行列式:
\[{\displaystyle
{\begin{vmatrix}a_{1,1}&a_{1,2}\\a_{2,1}&a_{2,2}\end{vmatrix}}=a_{1,1}a_{2,2}-a_{1,2}a_{2,1}}\]
3阶矩阵的行列式:
\[{\displaystyle \displaystyle
{\begin{vmatrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{vmatrix}}=a_{1,1}a_{2,2}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}+a_{1,3}a_{2,1}a_{3,2}-a_{1,3}a_{2,2}a_{3,1}-a_{1,1}a_{2,3}a_{3,2}-a_{1,2}a_{2,1}a_{3,3}}\]

几何意义:二维和三维欧氏空间中的例子
行列式的一个自然的源起是n维平行体的体积。行列式的定义和n维平行体的体积有着本质上的关联。
二维向量组的行列式
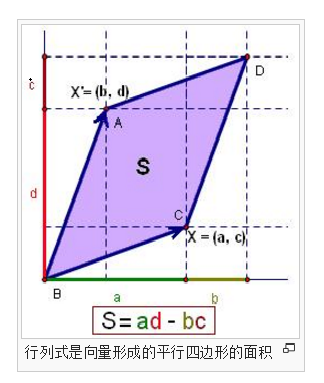
在一个二维平面上,两个向量X = (a, c)和X' = (b, d)的行列式是:
\[{\displaystyle
\det(X,X')={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc}
\]
比如说,两个向量X = (2, 1)和X' = (3, 4)的行列式是:
\[{\displaystyle
\det(X,X')={\begin{vmatrix}2&3\\1&4\end{vmatrix}}=2\cdot
4-3\cdot 1=5} \]
经计算可知,当系数是实数时,行列式表示的是向量X和X'形成的平行四边形的有向面积,并有如下性质:
行列式为零当且仅当两个向量共线(线性相关),这时平行四边形退化成一条直线[8]。
如果以逆时针方向为正向的话,有向面积的意义是:平行四边形面积为正当且仅当以原点为不动点将X逆时针“转到”X'处时,扫过的地方在平行四边形里,否则的话面积就是负的。如右图中,X和X'所构成的平行四边形的面积就是正的。
行列式是一个双线性映射。也就是说,\[{\displaystyle \det(\lambda X+\mu
Y,X')=\lambda \det(X,X')+\mu \det(Y,X')\;} \]
并且
\[{\displaystyle \det(X,\lambda X'+\mu
Y')=\lambda \det(X,X')+\mu \det(X,Y')\;} \]
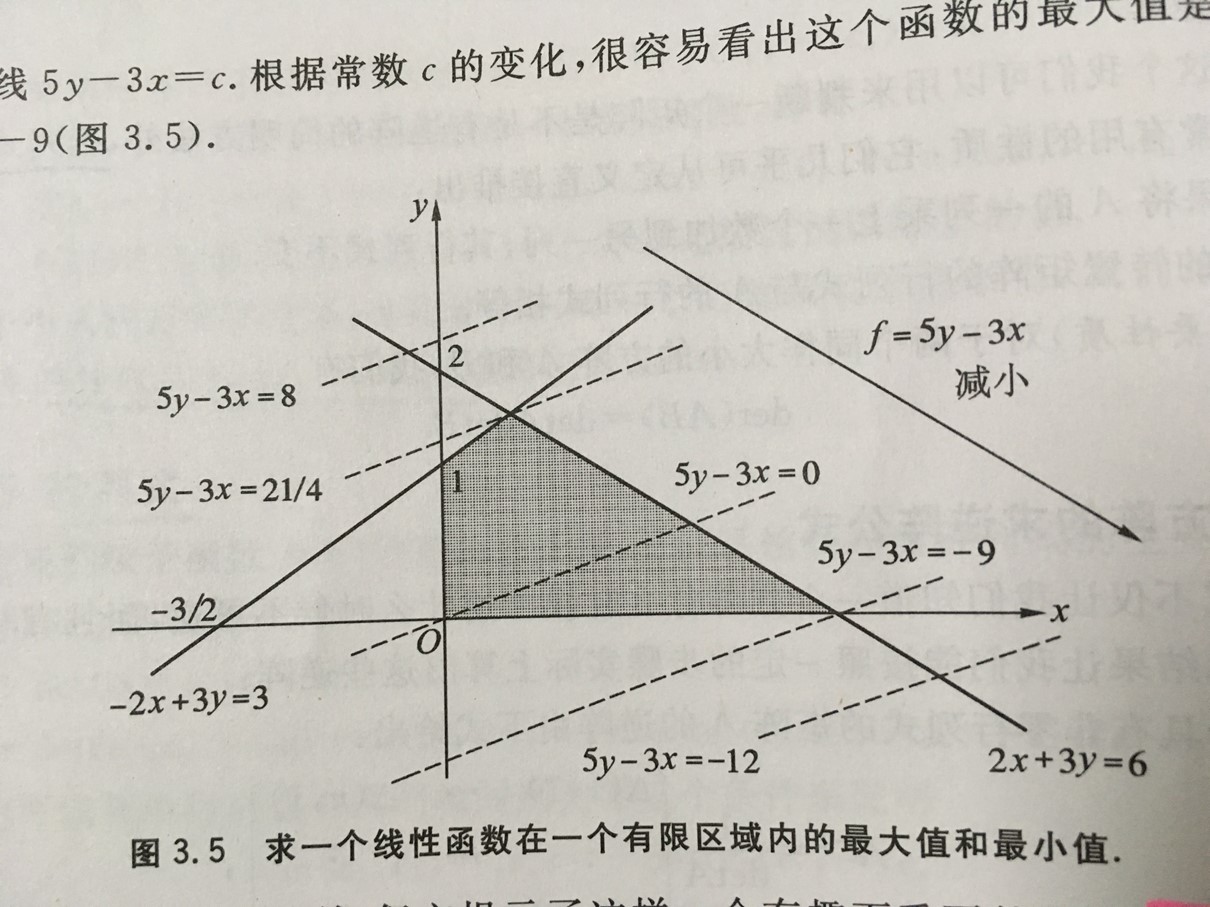
6、最优化
1)线性约束
给定一些约束方程的条件下求得某个量的一个最优值或最大值。
函数的最大和最小值都出现在区域的顶点上。
凸区域:区域中任何两点都可以被一条不与边界相交的直线段连接起来。
2)单纯形法


7、距离、长度、角度
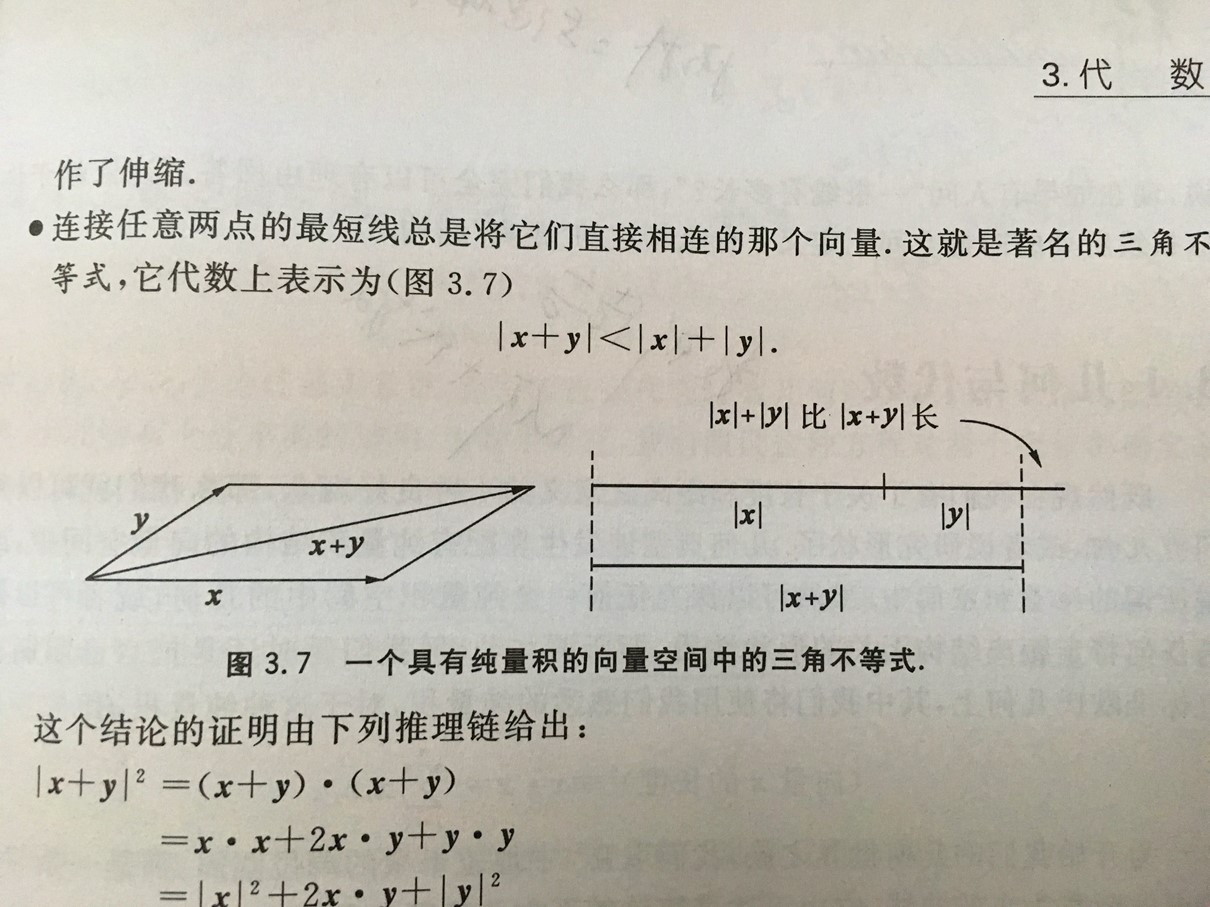
从一个向量到一个标量的运算:纯量积(点积),符号是:·
例如x·y表示向量x与向量y的距离。
两个向量\[{\displaystyle {\vec {a}}} =
[a_{1}, a_{2}, …, a_{n}] \]和\[{\displaystyle {\vec {b}}} = [b_{1}, b_{2}, …,
b_{n}] \]的点积定义为:
\[{\displaystyle {\vec {a}}\cdot {\vec
{b}}=\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}
\]
定义向量的长度
\[{|x|=\sqrt {x\cdot x}}\]
角度及点积的几何意义:
几何定义:在欧几里得空间中,点积可以直观地定义为
\[{\displaystyle {\vec {a}}\cdot {\vec
{b}}=|{\vec {a}}|\,|{\vec {b}}|\cos \theta \;} \] 这里 |\({\displaystyle {\vec {x}}}\)| 表示 \({\displaystyle {\vec {x}}}\)
的模(长度),θ表示两个向量之间的角度。
注意:点积的形式定义和这个定义不同;在形式定义中,\({\displaystyle {\vec {a}}}\) 和 \({\displaystyle {\vec {b}}}\)
的夹角是通过上述等式定义的。
这样,两个互相垂直的向量的点积总是零。若\({\displaystyle {\vec {a}}}\) 和\({\displaystyle {\vec {b}}}\)
都是单位向量(长度为1),它们的点积就是它们的夹角的余弦。那么,给定两个向量,它们之间的夹角可以通过下列公式得到:
\[{\displaystyle \cos {\theta }={\frac
{\mathbf {a\cdot b} }{|{\vec {a}}|\,|{\vec {b}}|}}} \]
这个运算可以简单地理解为:在点积运算中,第一个向量投影到第二个向量上(这里,向量的顺序是不重要的,点积运算是可交换的),然后通过除以它们的标量长度来“标准化”。这样,这个分数一定是小于等于1的,可以简单地转化成一个角度值。
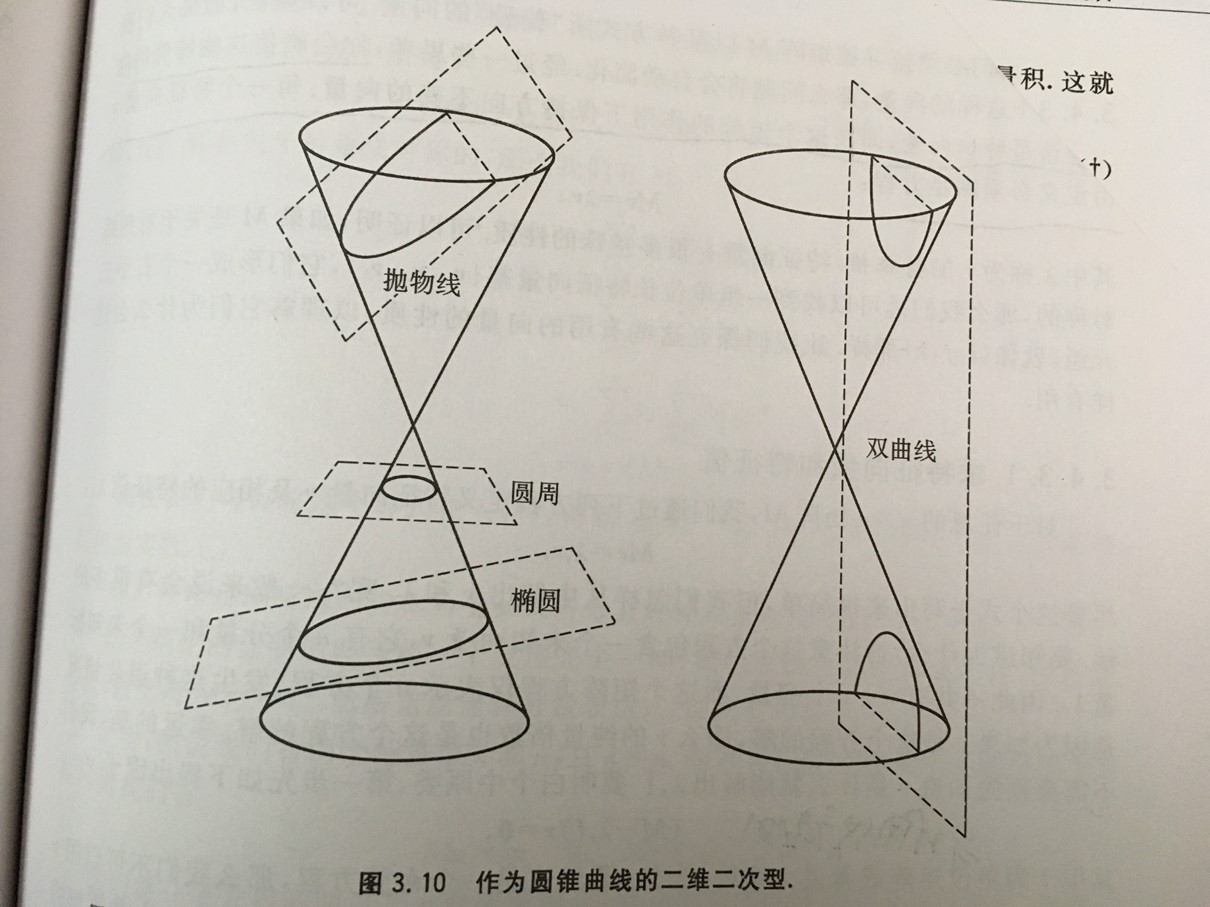
8、二维空间的二次型
ax²+bx+cy²+exy=f
通过配平方把x,y的线性项去掉。变成形式Ax²+Bxy+Cy²=D;利用二次方程求解公式可求。
这些解有六种情况:圆周、椭圆、双曲线、抛物线、直线、点;
如下图:(用一个平面去切割一个圆锥)
9、特征向量和特征值

重点研究实对称矩阵的特殊性质:
- 实对称矩阵的特征值总是实数;
- 对称矩阵的两个特征向量如果对应的特征值不同,那么他们相交;
- 从任何一个n*n实对称矩阵M的特征值向量集合总,总可以为R^n选取一组标准正交基。
应用:特征脸。
在图像处理中,脸部图像的处理可以看作分量为每个像素的灰度的向量。该向量空间的维数是像素的个数。一个标准化面部图形的一个大型数据集合的协方差矩阵的特征向量称为特征脸。它们对于将任何面部图像表达为它们的线性组合非常有用。特征脸提供了一种用于识别目的的数据压缩的方式。在这个应用中,一般只取那些最大特征值所对应的特征脸。
10、对称
对称群:简称群。任何满足群公理的系统均可被认为是一个由对称组成的相容集合。



下一篇:《数学桥--对高等数学的一次观赏之旅》读书心得之四