《数学桥--对高等数学的一次观赏之旅》读书心得之一
一本非常烧脑的书!光是看书就花了四周,做笔记又花了一周。
看完《无言的宇宙--隐藏在24个数学公式背后的故事》之后,想深入了解那些数学的定理,就决定重捡起这本书看看(书是之前买的,但因为比较深奥,当时就没看)。看的过程,仿佛就是重温了一遍大学的高等数学。
不过本书重点是体现数学的思想,对一些深奥的、细节的问题倒是一带而过,所以看起来还是能把高等数学中核心的部分及思想体会一遍。
本书最大的特点是,根据人类在认识自然、解决生活中实际问题的要求,自然而然带出数学的相关领域。例如从自然数到整数,从整数到分数,从分数到有理数、到无理数,从实数到复数等等。这些数的出现,不是数学家凭空想出来的,而是人们结合需要一步步的扩展来的。在数学发展的过程中,集合慢慢替代了数成为了数学的基本要素,集合的概念在数学中发挥了重大的作用。数学的不同领域,其实就是定义满足一定公理、定义、运算要求的一些符合条件元素的集合,然后在这些公理、定义上,用形式化的符合来对这个集合进行研究和推理,形成了一个完整的领域。例如欧式几何、罗氏几何、黎曼几何,例如群论,例如高维数系等等。
数学的思想:
- 1)实际需求(问题) ;
- 2)定义形式 ;
- 3)对形式进行条件约束 ;
- 4)证明这些约束满足实际的需求(问题);
- 5)抽象出定理并推广到一般的情况。
类似:1)要把一个东西快速运到另外一个地方; 2)定义一个叫车的东西; 3)车必须满足,能开动、速度要达到多少、装载容量、安全等等; 4)证明这个车符合实际的需求; 5)推广到运输工具(包括运人等)。
一、数


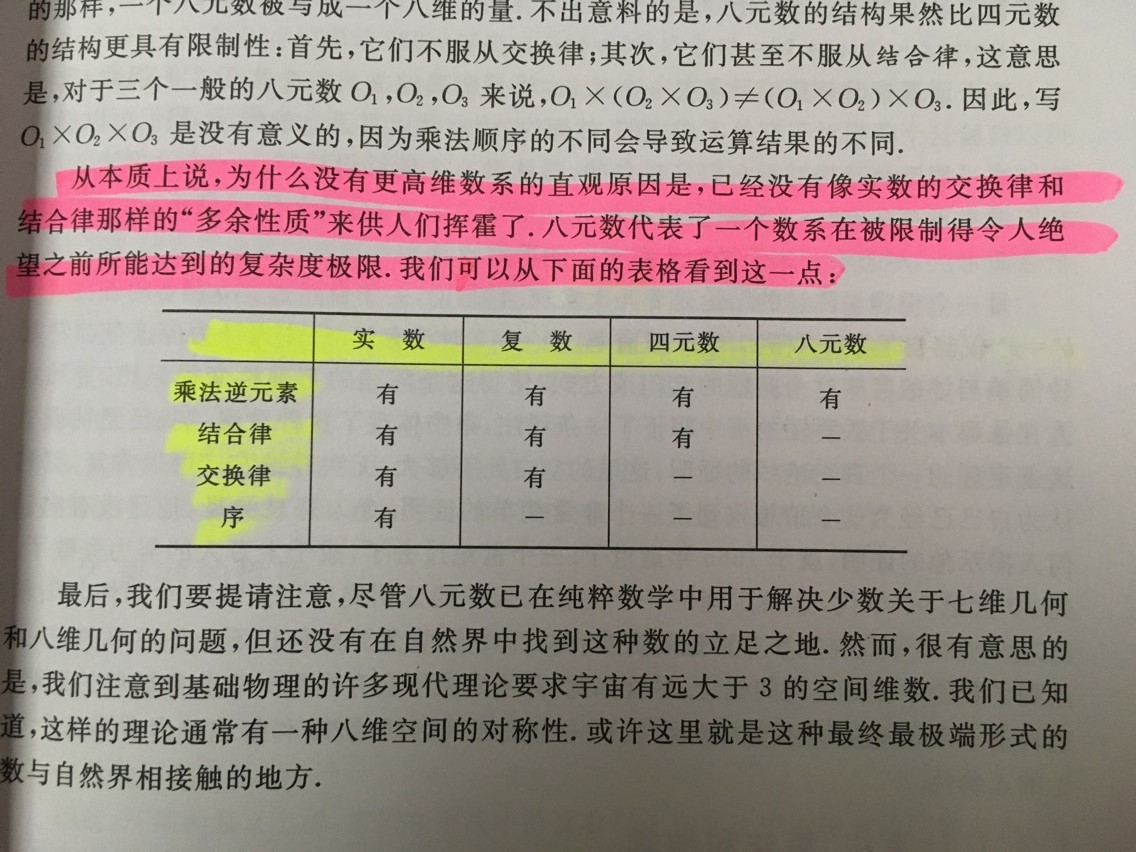
- 代数数:就是一个整数系多项式方程的实数根;例如\(\sqrt {2}\)
超越数:就是任何不是代数数的实根;例如π。
- 哥德巴赫猜想:所有大于2的偶数都可以写成两个素数的和。
- 拓扑:研究与任何特定距离结构无关的形状的性质。
1、求两个数的最大公因数
长除法。




2、连分数

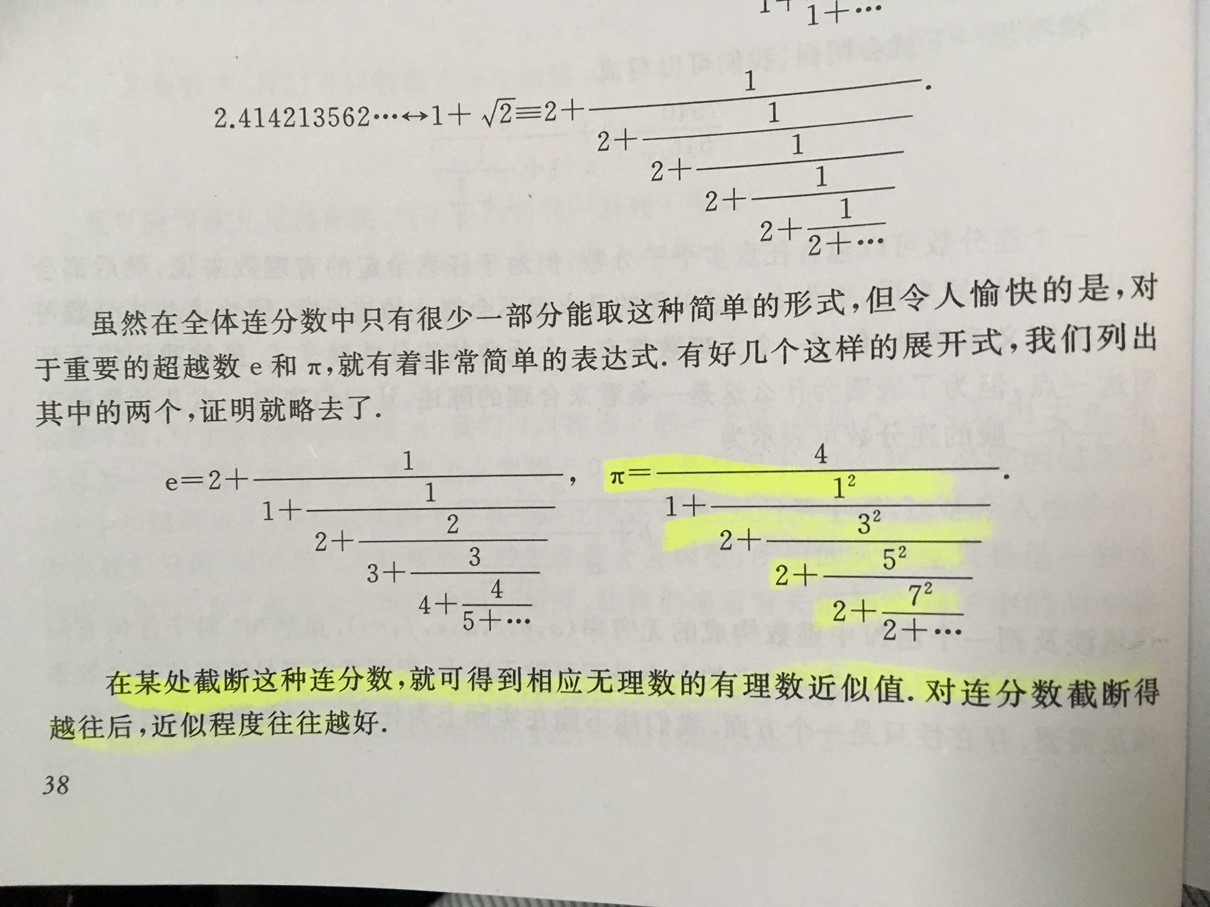
3、RSA密码

下一篇:《数学桥--对高等数学的一次观赏之旅》读书心得之二
