《无言的宇宙--隐藏在24个数学公式背后的故事》读书心得之二

接上篇：《无言的宇宙--隐藏在24个数学公式背后的故事》读书心得之一

第二部分：探索时代的定理

7.口吃者的秘密：卡尔达诺公式

卡尔达诺公式具有长期的影响，甚至超过了它所解决的问题本身的重要意义。例如，它是首次吸引人们在数学中使用虚数和复数的事物之一。虚数是平方为负数的数字，这是任何实数都不具有的性质。有了虚数我们就可以宣传：-1有两个平方根，他分别可以以\(i\) 和\(-i\) 记之。没有虚数，我们就只能说-1没有平方根。一旦有了虚数，我们就可以把复数定义为带有实数与虚数的两个部分的数，例如\(1+2i\) 。
如果没有虚数，不但现代数学无法想象，就连现代物理也同样无法想象。
在征服了三次与四次方程之后，1824年，挪威数学家终于证明，对已五次方程，不存在任何卡尔达诺式的求解公式。

8.九重天上的秩序：开普勒的行星运行定律

9.书写永恒：费马最后定理

1993年，怀尔斯宣布他证明了费马大定理。

10.一片未曾探索过的大陆：微积分基本定理

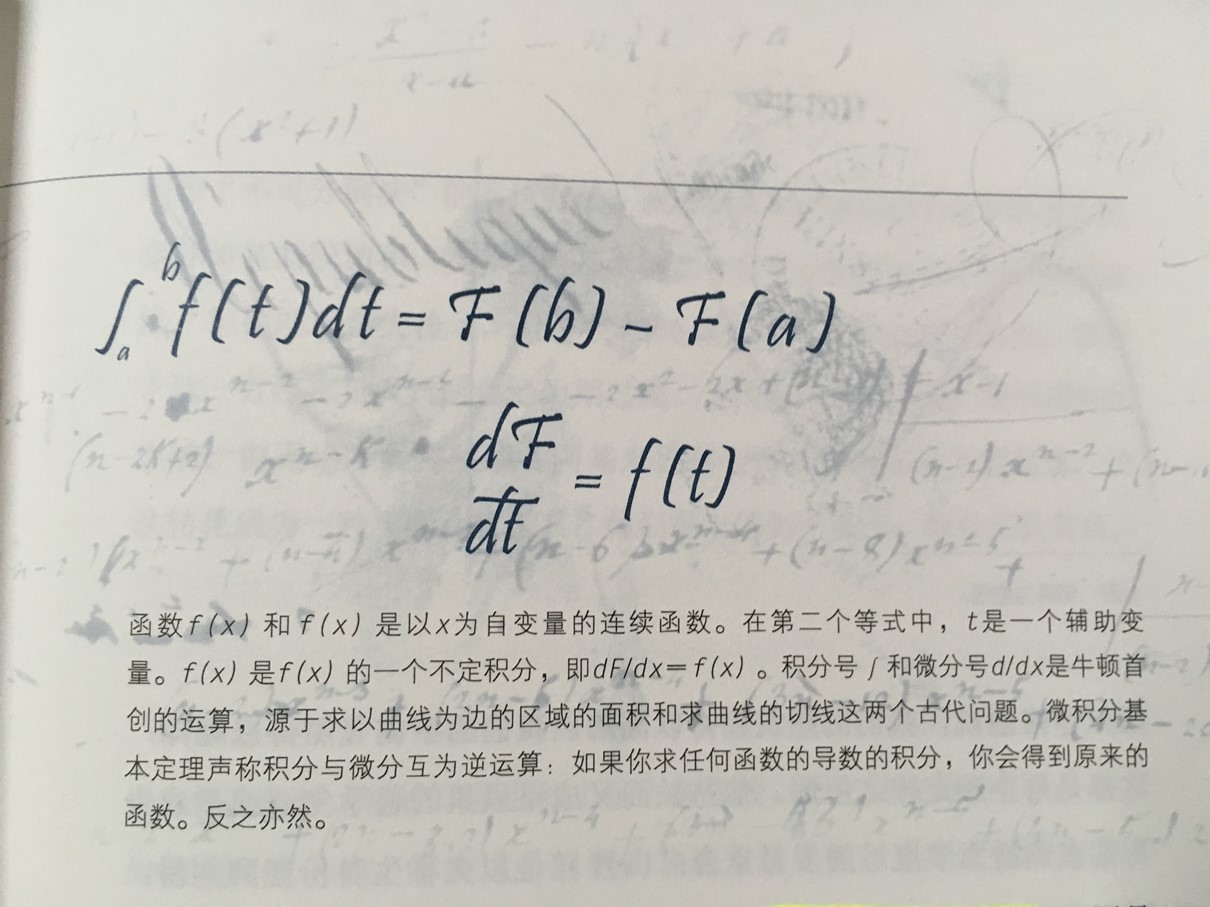
在17世纪，数学家们确实发现了他们相当于“美洲新大陆”的发现，这是一块未经探索的数学“大陆”。这片大陆的名字叫做“微积分”。
莱布尼兹也有许多数学意外的兴趣。作为哲学家，可以举出他在著作中有关邪恶的例子；他认为，尽管有些邪恶是必需的，但上帝创造了“一切可能的世界中最美好的一个”。
一条曲线的切线的斜率就是那个图形所代表的函数的变化率。
解决求切线问题的微分和解决求积问题的积分。微分和积分互为逆运算。

为什么说这一发现开发了数学的新大陆呢？因为它最终让数学彻底掌握了连续变化的概念。在莱布尼兹和牛顿之前，数学家们一直被局限于静止的图像或者离散数量的桎梏(gù)之内，连续运动与连续变化的数量之世界与他们世界绝缘。但整个现代科学都是关于变化的科学。数学家们在微积分中找到了他们投身现代科学的必要工具。

11.关于苹果、传说……以及彗星：牛顿定律

牛顿的《自然哲学的数学原理》对物理学的重要意义等同于欧几里得的《几何原本》对几何学的意义。

• 牛顿第一定律：运动物体将永远保持匀速直线运动，除非有外力将其停止或者改变其运动方向。
  
• 牛顿第二定律：作用在物理上的力等于其动量的变化率。\(F=\dfrac{d\left( mv\right) }{dt}=ma\)
  
• 牛顿第三定律：对于任何一个作用力，都存在一个与它大小相等方向相反的反作用力。

牛顿真正独树一帜的成就就是他运用微积分，把引力定律和它运动定律结合，从而建立并随之解决了描述行星轨道的方程的能力。

12.伟大的探索者：欧拉定理

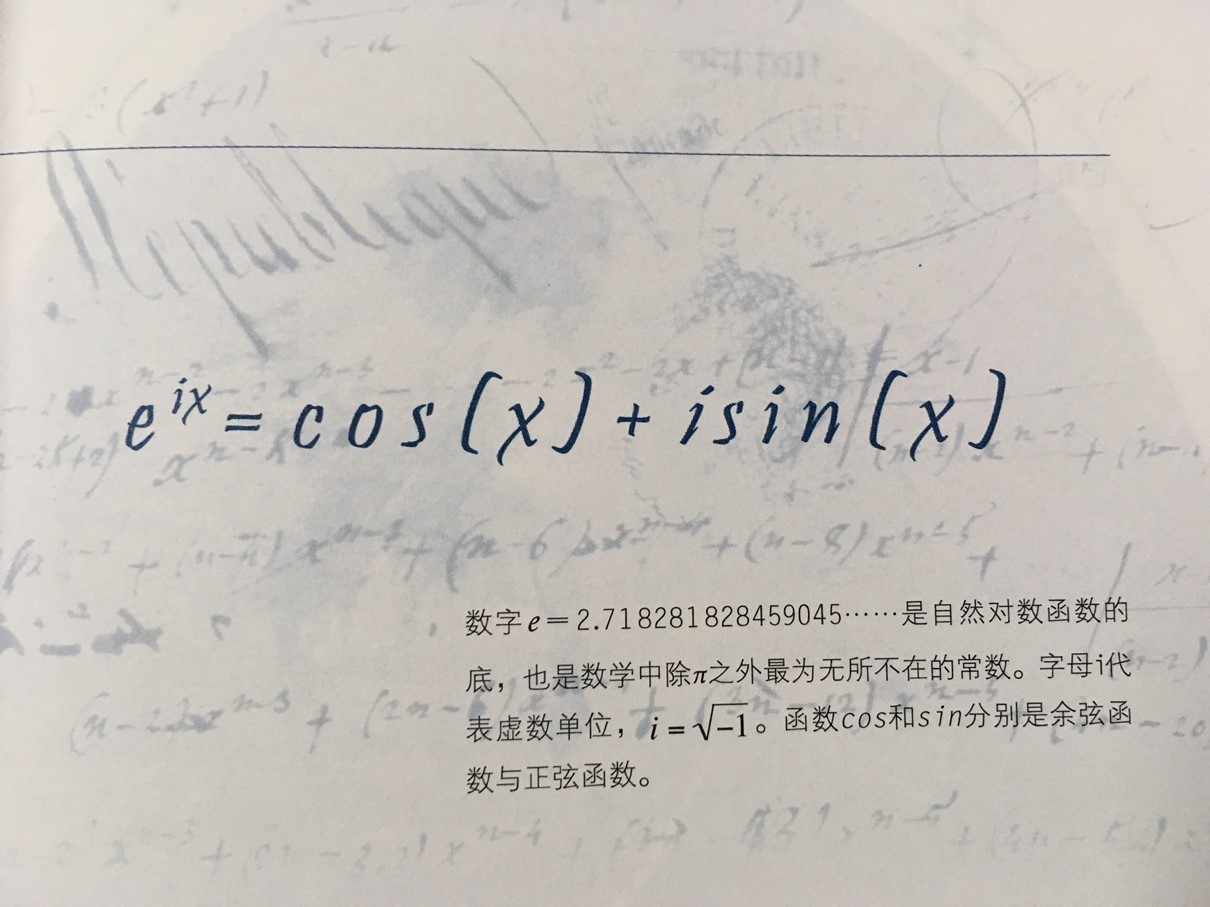
微积分中最重要的函数或许就是指数函数\(exp(x)\) ，因为这是唯一一个导数和积分都是它本身的函数。
\(exp(ix)=cos(x)+isin(x)\)
这是欧拉本人认为最重要的公式，它把微积分中最终的\(exp、cos、sin\) 三个函数联系在了一起。
欧拉是一个光辉的特例，他发表了大量的著作，他以实际行动作为人们的榜样，带领他人前进，并对数学得以发展到今天的状况作出了贡献：今天的数学是一项职业，有关数学的信息不存在专利，而是公之于众，供大家分享。

下一篇：《无言的宇宙--隐藏在24个数学公式背后的故事》读书心得之三