《无言的宇宙--隐藏在24个数学公式背后的故事》读书心得之三

接上篇：《无言的宇宙--隐藏在24个数学公式背后的故事》读书心得之二

第三部分：普罗米修斯时代的定理

革命的爆发经常是有那些对自己正在做些什么一无所知的人点燃引线的。

13.新的代数：汉密尔顿与四元数

四元数完全出自一个人的想象之中，是新代数的第一个例子。这一步骤与其他数学家对于新集合和新函数的发现几乎同步，这些发现共同作用，把数学家从传统的结构与束缚中解放了出来。有史以来第一次，数学家们可以在物质世界之外探险，他们可以自由自在地发明了一个全新的世界。（个人注：抽象代数）
现在的问题不再是哪些结构是可能的，而是哪些结构值得研究。一个新结构会有助于解决已经存在的问题吗？它会有深刻的、富有挑战性的、有其固有美感的理论吗？

14.两颗流星：群论

1858年，查尔斯·艾尔米特证明，任何五次多项式方程的解不能用有限目的的\(+ - x ÷ 和 \sqrt{x}\) 来表达，但是可以用一种新型函数写出，这种函数名为椭圆函数，是阿贝尔发现的。
这是正常的人类对难题的反应：如果你无法用现有的工具克服困难，那就发明新工具好了。
群的概念现在已经变成了数学家用以表达对称这一古老想法的主要工具。化学家在运用群论描述晶体对称性。物理学家运用群论描述粒子的对称性。

15.鲸鱼几何与蚂蚁几何：非欧几何

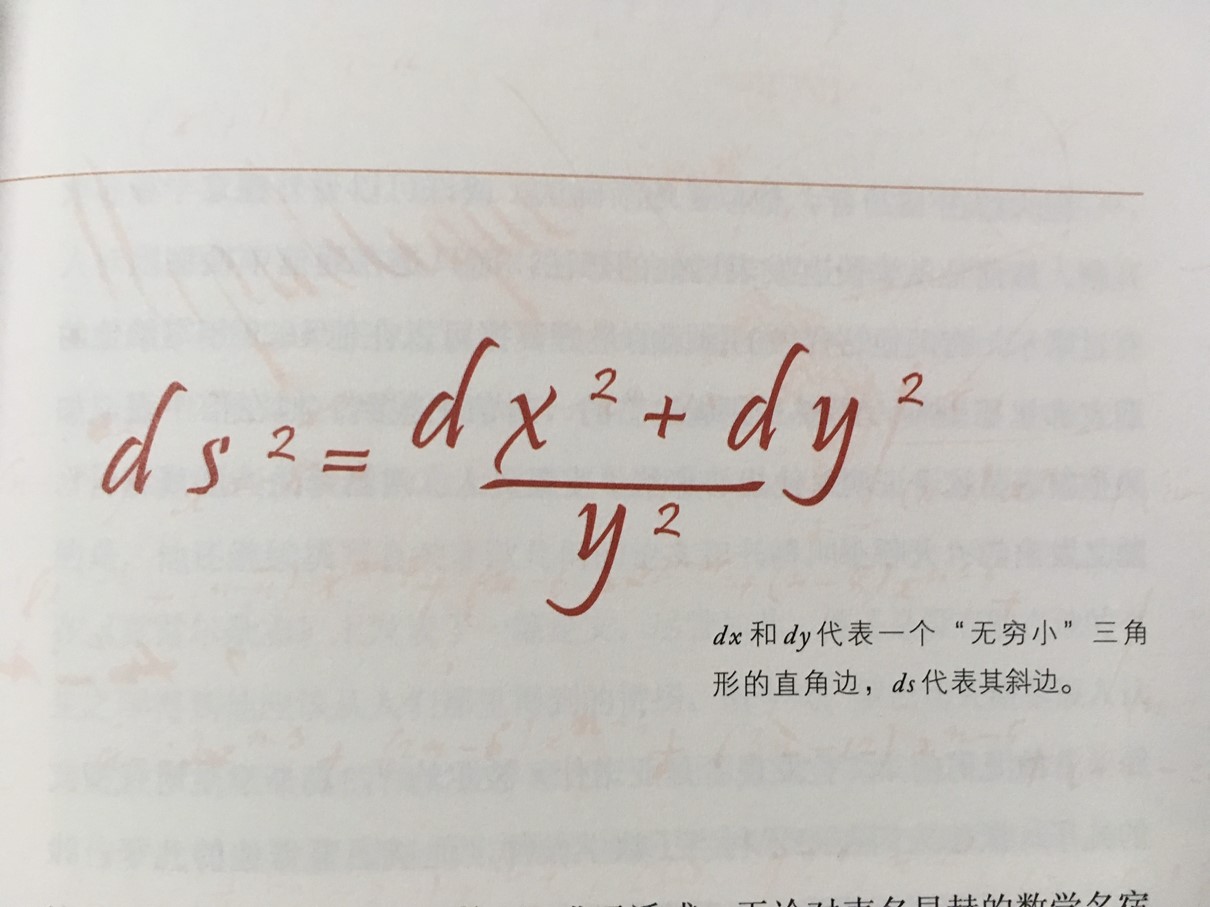
第五条公设说：同一平面内一条直线a和另外两条直线b.c相交，若在a某一侧的两个内角的和小于两直角，则b.c两直线经无限延长后在该侧相交。
按几何特性（曲率），现存非欧几何的类型可以概括如下：

• 坚持第五公设，引出欧几里得几何。
  
• 以“可以引最少两条平行线”为新公设，引出罗氏几何（或称双曲面几何）。
  
• 以“一条平行线也不能引”为新公设，引出黎曼几何（或称椭圆几何）。

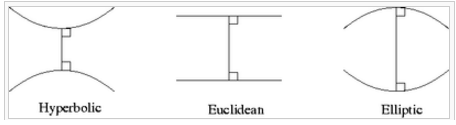
这三种几何学，都是常曲率空间中的几何学，分别对应曲率为0、负常数和正常数的情况。
三种几何中垂直于同一线段的两条直线的图象

16.我们信赖质数：质数定理

当高斯1796年还在大学就读时，他便证明了正十七边形可以用尺规作图法画出。
正是通过所有质数的乘法运算，才组成了所有其它的一切数字。在这种意义上，它们就像化学中的元素那样基本。

17.关于谱系的想法：傅立叶级数

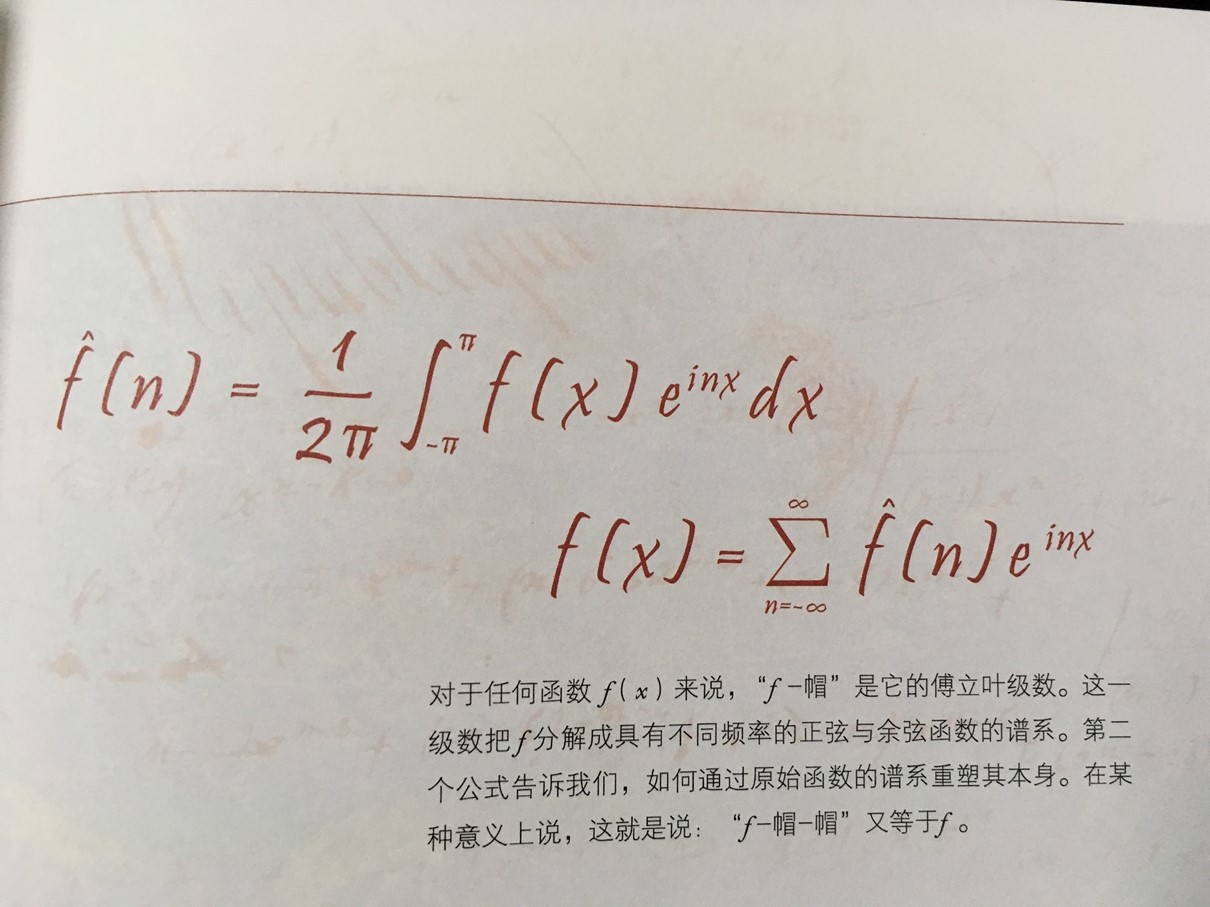
18.上帝之眼中看到的光：麦克斯韦方程

磁场是由电流产生的。电场是由变化的磁场引发的。而且说到底，光只不过就是传播中的电磁波。
时光荏苒：rěn rǎn 荏苒：时间一点一点的流逝。指时间渐渐地过去了。

下一篇：《无言的宇宙--隐藏在24个数学公式背后的故事》读书心得之四