《无言的宇宙--隐藏在24个数学公式背后的故事》读书心得之一
一本科普性质的数学书,作者摘选了24条在人类历史上最重要的数学公式(物理公式),介绍其背景及原理等。
像作者所说,数学是表达宇宙的一种语言。看了本书之后,这些公式的优美,但背后揭示出宇宙本质的深刻程度,让人叹为观止。
数学是一门科学,从毕达哥拉斯与柏拉图起希腊哲学家就对数学有着崇高的评价,他们将其视为纯理性的科学,认为它能穿透实际世界虚幻的表面,洞悉其实质;同时,数学也是一门艺术,它追求简单、优美。
下面,就让我们跟随作者的步伐,领略这些美妙绝伦的公式吧。
第一部分:古代的定理
1.我们为什么信赖算术:世界上最简单的公式

阿拉伯数字然让数学民主化了。以前的数学都是精英阶层的专利。数学史的发展就是让数学普及开了,但是现在的高等数学,走向了抽象化的道路,又进入了精英阶层的专利了。
大部分数学家强烈的感受到,数字,以及我们研究的大量其他数学创造物,都代表了人超越了人类思维的客观现实。如果是这样,出现能证明1+1既等于2又等于3这类矛盾陈述的可能性就微乎其微。逻辑家们将之称为“柏拉图主义者”的观点。“典型的数学家在工作日是柏拉图主义者,而在星期天是形式主义者。”
与任何其它语言、宗教或信仰系统相比,在穿越文化与时间界限方面算术最为成功。的确,搜寻地外生物的科学家经常假定,我们能够解码的第一份来自地外世界的信息将以数学形式发送,因为数学是最为广泛接受的宇宙通用语言。
2.抗拒新概念:零的发现

现代数学对于零的重要性的强调通常毫无过分之处。数学家们把它称为单位元素,因为把它加到任何数字上,都不会改变那个数字。单位元素对数学的重要性就相当于同义词对文学的重要性。
3.斜边的平方:毕达哥拉斯定理

毕达哥拉斯认为,世界万物都是由数字统治的。
质数对现代密码学至关重要。现代密码学很大的一部分基于如下理念:对于一个很大的合数,比如一个有几百位数的合数,找到它的质因子十分困难。
归谬法,也称反证法,在早期的数学证明中是非常有用的一个工具。
4.圆的游戏:π的发现


林德曼在1882年证明了关于π的另外一个更为微妙的事实:它是一个超越数(不能以任何系统为有理数多项式方程的解来表示,例如\(\sqrt{2}\)
不是一个超越数,因为它是方程x²=2的解),一种加强版的无理数。
5.从芝诺悖论谈起:无穷的概念

古代希腊人都还对无穷大这一概念没有把握,是他们无法取极限。
几何级数的各项按某一常数比逐项递减。
6.杠杆作用的重要性:杠杆原理
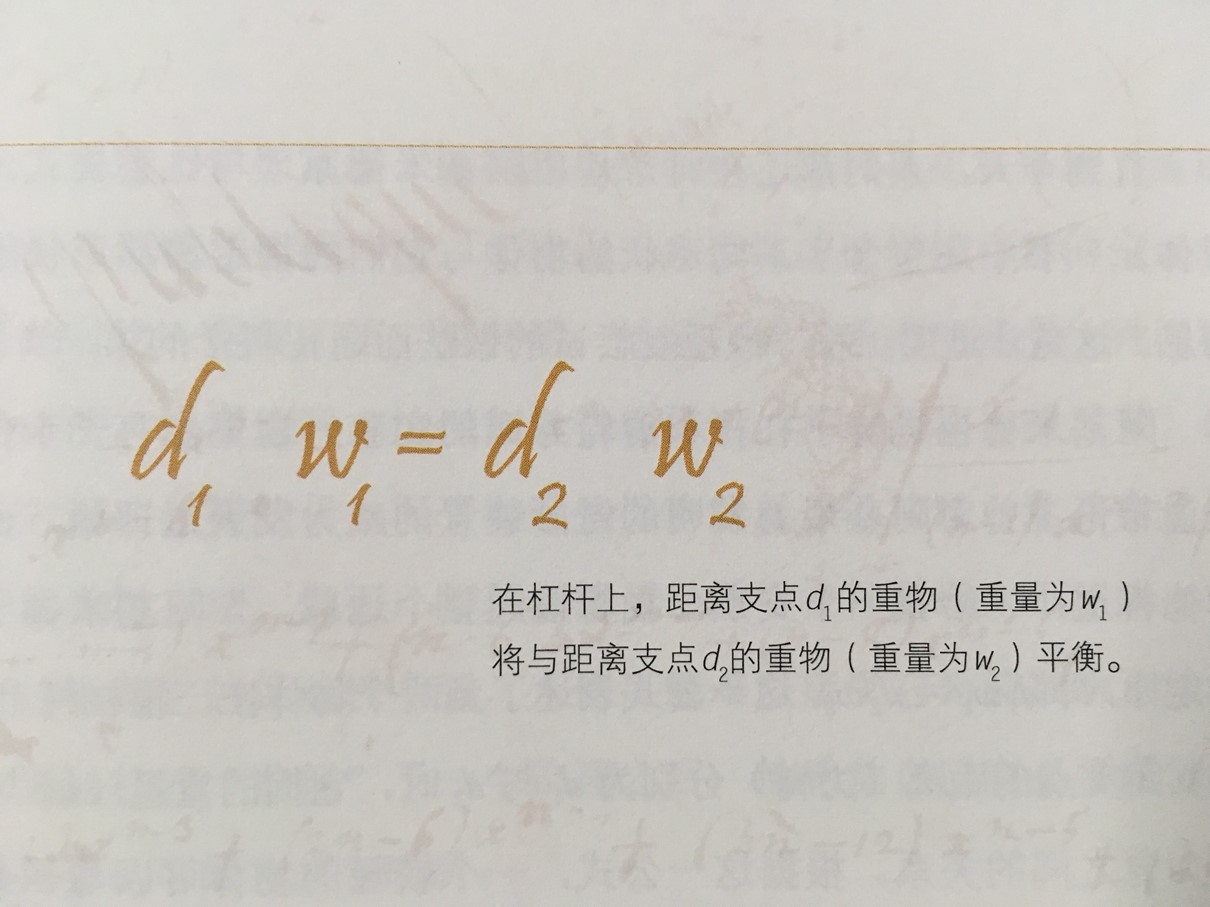
阿基米德他最引以为豪的成果是他证明了球体体积是它的外接圆柱体体积的三分之二,或可以等价的将此公式表达为:\(V=\dfrac{4}{3}πr³\)
。他甚至要求人们在他的墓碑上刻此球体和它的外接圆柱体的图像。
下一篇:《无言的宇宙--隐藏在24个数学公式背后的故事》读书心得之二
